具有心理效应的媒介传染病模型的研究

王 琪，薛亚奎

（中北大学 理学院，太原 030051）

媒介传染病是一种重要的传染病，是由受感染的节肢动物传播的疾病，如蚊子、扁虱等。一个世纪以前就有证据表明，吸血节肢动物能够向人类以及动物和人类之间传播特定类型的病毒、细菌、原生动物和蠕虫。自那时以来，有大量媒介传播疾病爆发的报告，如疟疾、登革热、南美锥虫病和利什曼病，根据世界卫生组织（WHO）的数据，媒介传播疾病占所有传染病病例的17% 以上，每年导致超过100万人死亡［1］，媒介传染病严重威胁着人类的健康。因此针对媒介传染病，很多数学工作者通过建立数学模型进行理论分析和定量研究［2-7］。文献［8］对于虫媒传染病SEIR模型进行了分析和模拟，文献［9］介绍了在埃及伊蚊的Zika病毒的垂直传染，表明了垂直传染可能提供了一个潜在的机制，病毒会在恶劣的条件下生存。

了解人类行为及社会反映对传染病传播的影响是加强控制工作的关键。疾病发生率在传播过程中其重要作用，在大部分动力学模型中使用的是双线性发生率βSI，而当越来越多的染病病例被媒体报道后，人们的防护意识会增强，使得实际染病者数量降低。在文献［10-15］中使用非单调发生函数模拟了这种现象。因而本文综合考虑了一类具有心理效应及垂直传播的媒介传染病SEIRS模型，由于心理效应的影响，染病媒介与易感人群之间采用发生率

1 动力学模型

本文把疾病流行区域或国家的总人口分为易感类、潜伏类、染病类、移出类等4类，分别用SH（t）、EH（t）、IH（t）、RH（t）表示t时刻的易感类、潜伏类、染病类、移出类的人口数量。假设染病类的后代以p的概率具有先天免疫，则以（1-p）的概率进入潜伏类，用NH（t）表示t时刻的总人数，则NH（t）=SH（t）+EH（t）+IH（t）+RH（t）。将媒介分为易感和感染等2类，分别用SV（t），IV（t）表示t时刻的易感类和感染类媒介的数量，用NV（t）表示t时刻的媒介总数，则NV（t）=SV（t）+IV（t）。建立模型如下：

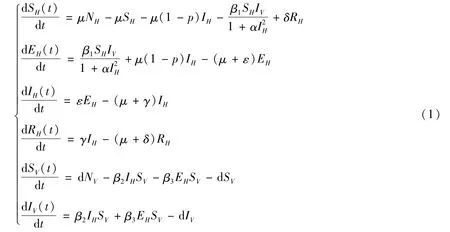
式中：假设不考虑因病死亡，媒介的出生和死亡率相等均用d表示，人口的出生和死亡率系数相等均用μ表示；β1表示人的心理对疾病的感染强度；表示当染病人群的数量达到一定数量后，易感者行为改变的心理效应；β2表示染病类人群对易感媒介的感染率；β3表示潜伏类人群对易感媒介的感染率；ε表示潜伏者发病成染病者的概率；γ表示染病者的康复率；δ表示移出者再次感染的概率。

不妨令：NH（t）=SH（t）+EH（t）+IH（t）+RH（t）=NH0，NV（t）=SV（t）+IV（t）=NV0，设：

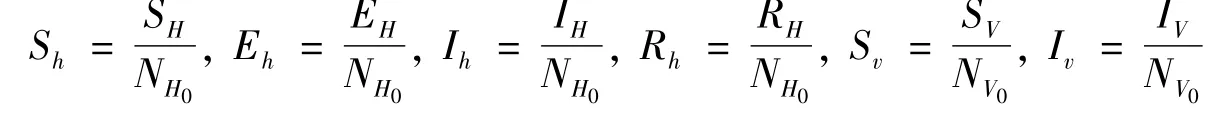
则有：

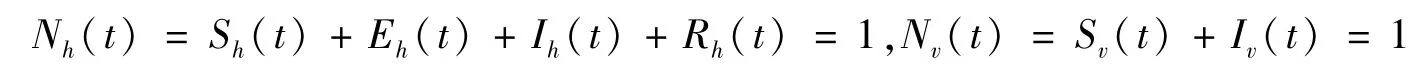
进一步，模型（1）可以化简为：

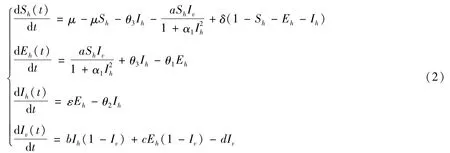
为方便讨论，记θ1=μ+ε，θ2=μ+γ，θ3=μ（1-p），θ4=μ+δ，α1=αN2H0，a=β1NV0，b=β2NH0，c=β3NH0，显然：Ω=｛（Sh，Eh，Ih，Iv）∈R4+：0≤Sh+Eh+Ih≤1，0≤Iv≤1｝是模型（2）的一个正向不变集，下面将在集合Ω中研究模型（2）的动力学性态。

2 基本再生数及平衡点的存在性

2.1 基本再生数及无病平衡点的存在性

易知模型（2）总存在无病平衡点E0=（1，0，0，0），根据下一代矩阵法，求得基本再生数R0的表达式为：

显然θ1θ2-εθ3=μ2+εγ+μγ+μεp＞0。

2.2 地方病平衡点的存在性

为了得到模型的地方病平衡点E*=（S*h，E*h，I*h，I*v），令模型（2）方程的右端为0，并将S*h，E*h，I*h，I*v分别代入方程得到：

得到：

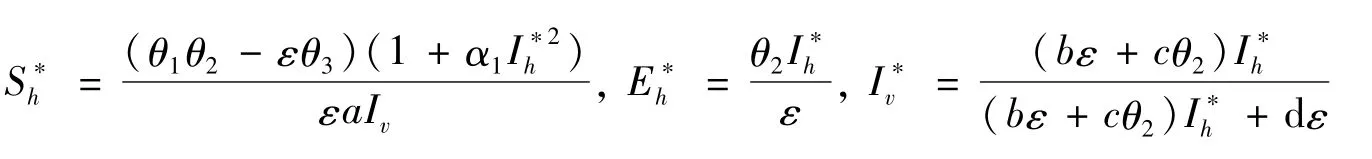
代入方程（4），有：

式中：a1=-α1（bε+cθ2）（θ1θ2-εθ3）θ4；a2=-α1dε（θ1θ2-εθ3）θ4；a3=-（bε+cθ2）（θ1θ2-εθ3）θ4-a（bε+cθ2）（θ1θ2+δθ2+δε）；a4=εa（bε+cθ2）θ4-dε（θ1θ2-εθ3）θ4。

则

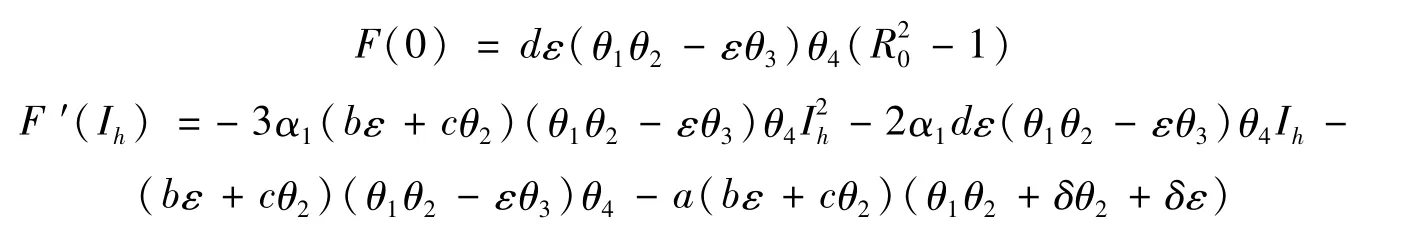
当Ih＞0时，F′（Ih）＜0，即F（Ih）＜F（0），因此，当R0＞1时，有F（0）＞0，则方程（8）有唯一正根I*h，模型（2）存在唯一的正平衡点E*=（S*h，E*h，I*h，I*v）。

定理1模型（2）一定存在无病平衡点E0，当R0＞1时，存在唯一地方病平衡点E*。

3 平衡点的稳定性

3.1 无病平衡点的稳定性

定理2对于模型（2），当R0＜1时，无病平衡点E0是全局渐近稳定的。

证明模型（2）在无病平衡点E0处的Jacobian矩阵为：

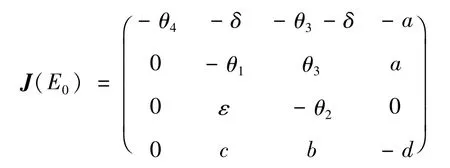
对J（E0）进行初等保号变换，有：

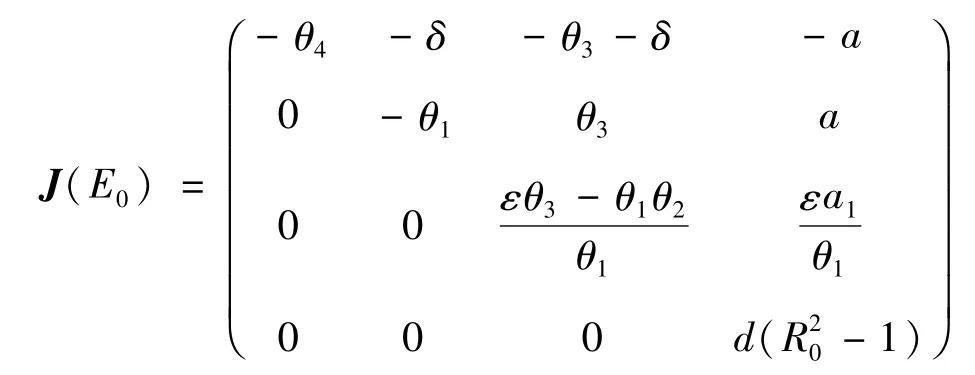
则J（E0）的特征方程对应的特征根为：

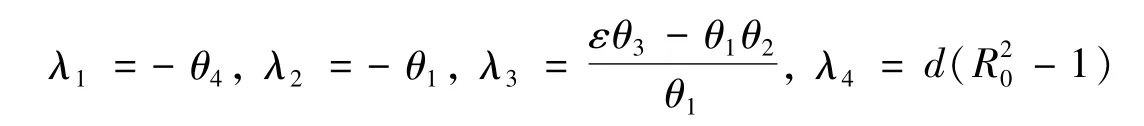
当R0＜1时，d（R20-1）＜0，即特征方程的所有特征根均有负实部。

因此，R0＜1时，无病平衡点E0是局部渐近稳定的。构造Lyapunov函数为：

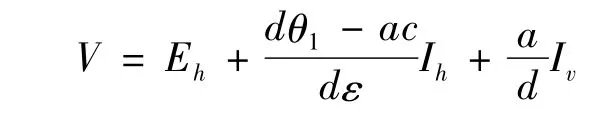
计算：

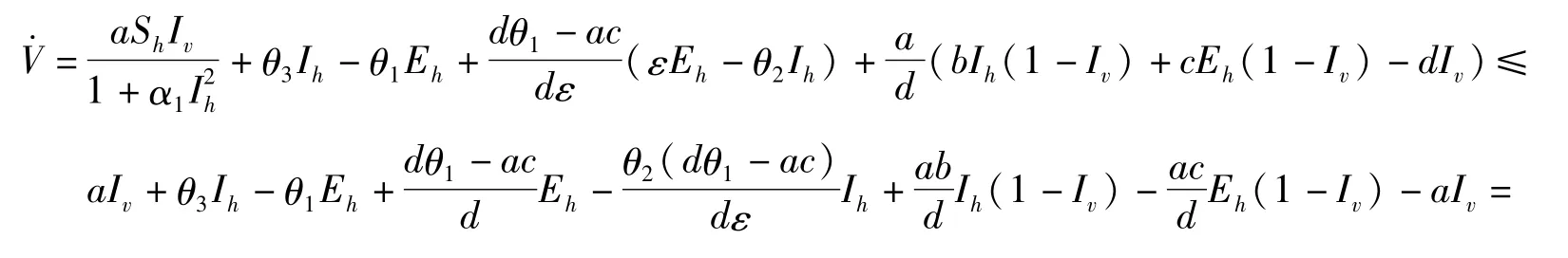
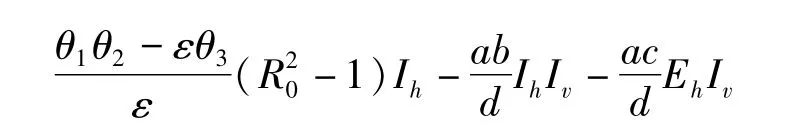
当R0＜1时，V·≤0，当且仅当Eh=Ih=0或Iv=Ih=0时，V·=0，由LaSalle不变集原理可知，E0在可行域内是全局渐近稳定的。证毕。

3.2 地方病平衡点的稳定性

定理3对于模型（2），当R0＞1时，地方病平衡点E*是局部渐近稳定的。

证明模型（2）在地方病平衡点E*处的Jacobian矩阵为：

对J（E*）进行初等保号变换，有：

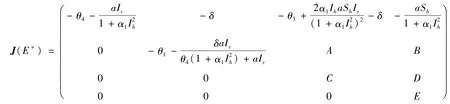
其中，

记

可得C＜0，E＜0，J（E*）特征方程对应的特征根为：

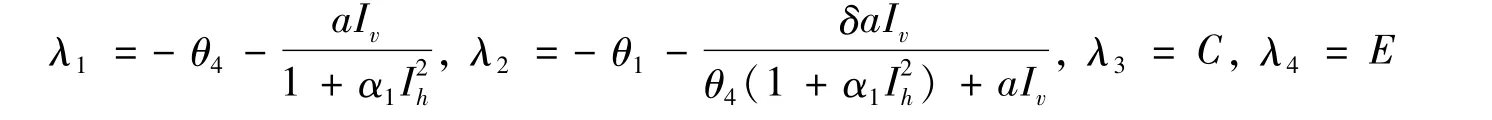
即特征方程所有的特征根均有负实部，因此模型（2）的地方病平衡点E*是局部渐近稳定的。证毕。

4 数值模拟

平衡点的稳定性模拟结果如图1所示。图1（a）中取参数μ=0.3，β1=0.072，p=0.37，β2=0.052，β3=0.023，γ=0.05，δ=0.05，ε=0.63，α=0.1，d=0.02。此时，R0=0.1193＜1，可以看出当R0＜1时，无病平衡点是全局渐近稳定的。图1（b）中取参数μ=0.3，β1=0.62，p=0.37，β2=0.52，β3=0.32，γ=0.05，δ=0.5，ε=0.63，α=0.7，d=0.7。此时，R0=1.2776＞1，可以看出当R0＞1时，地方病平衡点是局部渐近稳定的。

心理效应、媒介死亡率、染病媒介与易感人群的接触率对染病者的影响如图2所示。通过数值模拟说明了，心理效应对模型平衡点的稳定性并不会产生影响，但如果疾病流行，考虑心理效应会影响染病者的数量。并且得到当参数α和d增加或者β1减小时，染病者的数量会减少，选取“《中国疾病预防控制中心》全国法定传染病疫情概况”中2013年1月—10月全国甲型H1N1流感染病者的比例［16］，本文中绘制了染病者比例折线图，可以看出通过媒体、政府等各方面的宣传干预，人们预防疾病的意识增强，逐渐形成心理暗示后，染病者人数明显下降。从文献［17］中容易得到灭蚊行动对登革热疫情产生重要影响。以2013年中国大陆爆发的甲型H7N9禽流感为例，发病数最多的3个省份强制关闭了一些城市的大型活禽市场，尽管距离关闭活禽市场尚不足2个潜伏期，但新发病例报告数已出现大幅下降［18］。

图1 平衡点的稳定性模拟

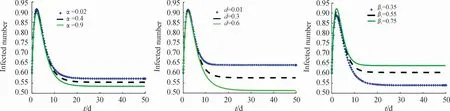
图2 心理效应、媒介死亡率、染病媒介与易感人群的接触率对染病者的影响

5 结论

研究了一类具有心理效应的媒介传染病，得到决定疾病是否流行的阈值R0，通过LaSalle不变集原理及构造Lyapunov函数，得到当R0＜1时，无病平衡点是全局渐近稳定的，当R0＞1时，得到唯一的地方病平衡点，并证明它在可行域内是局部渐近稳定的，通过数值模拟验证了结论的正确性。结果表明，考虑公众的心理并不会影响平衡点的稳定性，但如果疾病流行，会影响染病者的数量。本文通过理论分析及数值模拟证明了，缩短媒介的寿命、增强人们对疾病的信息接收以及减少易感人群与染病媒介的接触等方法，都对疾病的控制有所帮助。