基于电网最低运行成本的储能装置最佳接入位置研究

杨昌海，姜景芮，葛磊蛟，刘永成，杨婷婷，王 洲

（1.国网甘肃省电力公司经济技术研究院，兰州 730050；2.国网甘肃省电力公司，兰州 730030；3.天津大学 电气自动化与信息工程学院，天津 300072）

储能装置可以明显提高电力系统的可靠性［1］、调节波峰和波谷［2］、提升电网韧性［3］、修正系统功率因素以及降低电网的运营成本［4］，促进可再生能源消纳［5］，在提高分布式电源渗透率和并网可靠性方面发挥着巨大的作用。

在电网中科学配置储能装置的容量和接入位置是其发挥经济效益和技术效益的关键。文献［6-7］考虑多个DG并网后出现电网功率波动的情况，搭建计及储能装置容量的电力系统多目标优化配置模型。Yasser Moustafa［8］讨论了含风能电网中存储系统的分配问题。文献［9］研究了考虑热电联产和电动汽车调度的自主微电网储能容量优化策略。文献［10］以二氧化碳排放量为唯一目标变量优化最佳储能容量的配置。对于储能装置的经济效益，Moustafa［11］讨论了在含风电发电厂电网中储能装置的分配问题和电网整体的运行成本。文献［12］以发电成本的最小化为标准确定网络中每个储能装置的最佳位置和容量。文献［13］构建了储能装置在风电场中全寿命周期成本模型。文献［14］以最大效益为目标函数，配置光伏电站中储能装置的容量。文献［15］考虑政府补贴情况下，搭建了梯次电池储能装置平准化电度成本模型。文献［16］采用多目标非支配粒子群，建立储能装置投资及运营成本最小的多目标优化模型。Sortomme［17］利用PSO算法对微电网中可控负荷、发电机和储能装置的运行进行了优化。Kaldellis［18］分析了使用可再生资源和储能装置的发电成本。ShuliWen［19］以发电成本最小化为目标，确定储能装置接入网络中的最佳位置和容量。

以上研究均未充分考虑电力系统中负荷的波动对储能装置充放电状态及其运行成本的影响，另外，对电网的运行成本细化到每1 h进行计算的研究很少，所得结果和电网实际运行状态之间存在一定误差。但是，若要以系统运行成本最小化为目标确定储能装置的最佳位置，按照实际负荷的波动规律，精确计算系统运行成本最低情况下各发电机组运行状态得到的结果会更贴合实际。在综合考虑整个电力系统运行状态和成本的基础上，通过计算和对比储能装置在不同接入位置时，减小系统整体运行成本的程度，得到最佳接入位置才更具有实际的工程意义。

因此，本文在考虑电网中负荷波动性的基础上，细化日发电成本，构建计及储能装置的电网运行成本函数和约束条件，选择粒子群优化算法计算电网每1 h内的运行成本，得到在不含储能装置时，系统最低成本状态下各发电厂的出力。在此基础上，考虑储能装置的充放电状态及成本，通过对比有无储能装置时，储能系统不同接入位置情况下系统的运行成本，得到储能装置的最佳接入位置。最后，在IEEE-30节点系统中验证本文提出方法的可行性。

1 电网运行成本模型及约束条件

无论系统是否接入储能装置，系统日发电量发电的最小成本，等同于系统24 h内每小时的最小发电成本。

在无储能装置接入时，计算系统最低日发电成本下各个发电厂的出力，类似于解决最优潮流问题，即：根据网络的安全性、稳定性和物理约束等条件，假设发电厂每小时的发电量独立，考虑网络配置、发电机组的成本函数、每小时负荷，计算24 h内每小时的网络运行成本及网络损耗，最终得到最低成本下各个电厂每小时的发电量。

为计算储能装置的最佳位置，以无储能装置接入时发电机组出力的最优解作为初始值，考虑储能装置的运行成本，对比接入不同位置时整个电力系统的日发电成本，使系统日发电成本最低的位置即为储能装置最优接入位置。换言之，将确定储能装置接入电网的最佳位置转化为有无储能装置这两种情况下系统最低运行成本的比较问题。

1.1 假设条件

对于接入储能装置的电网，本文做出如下假设：

1）储能装置可以接入电网中的任意总线，接入后位置不变且24 h内不间断的投入使用。

2）24 h内的发电和放电量相等，放电时将其视为具有特定发电成本函数的发电机，储能装置接入的总线类型更改为P-V总线；充电时将其视为无附加载荷成本的负载，接入的总线类型更改为P-Q总线，若该总线有发电厂接入，则看作一个含负载的P-V总线，负载大小等于储能装置的充电功率。

1.2 目标函数

1.2.1 计及储能装置的电网运行成本函数

本文优化储能装置接入位置的目的是使日电量发电成本最小化。定义电网24 h内的计及储能装置的运行总成本F为：

式中，

式中，fh是第h个小时运行期间内的系统运行总成本，即：

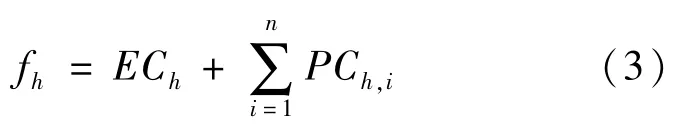
式中：ECh表示第h个小时运行期间内储能装置运行成本；PCh，i表示第i个发电厂在第h个小时运行期间内的运行成本，发电厂数为n。

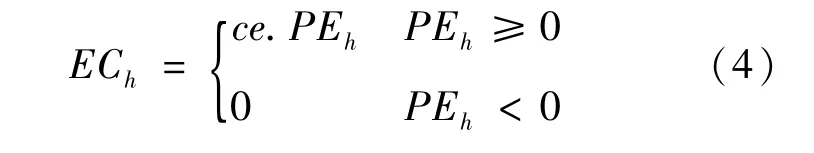
式中，ce表示有效储能装置线性成本指数。PE≥0时储能装置发电，当PE＜0时，储能装置储能。

式中：ai，bi，ci是第i个发电厂成本函数的系数。

1.2.2 计及储能装置的电网运行平等约束条件

1）某一时间段内电网发出和消耗的功率相同，即：

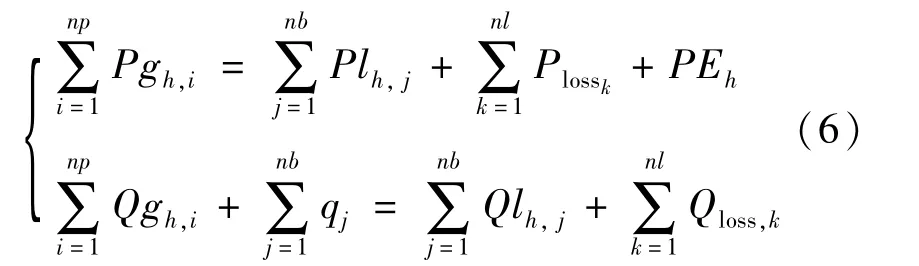
式中：Pgh，i和Qgh，i为发电厂i在h小时输出的有功和无功功率；qj为注入母线j的无功功率；Plh，j、Qlh，j表示母线j中的有功和无功功率；Plossk、Qlossk为线路k的有功和无功功率。网络母线和线路的数量分别为nb和nl。对储能装置充电时，PEh＞0；储能装置放电时，PEh＜0。

2）考虑到储能效率的影响，24 h内储能装置输入和输出的能量相同，即：

1.2.3 计及储能装置的电网运行不平等约束条件

1）电网母线电压、变压器分接头、发电厂功率和输电线路潮流的不平等约束为：

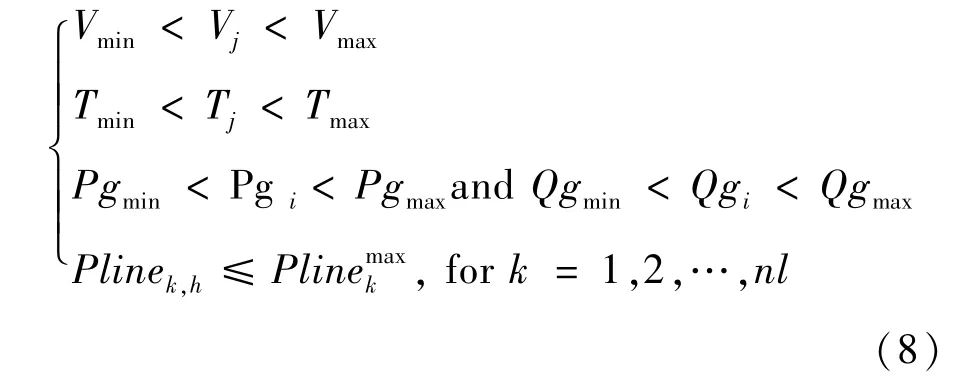
式中，Vj为母线j的电压，T为变压器j的分接头比，Pgi和Qgi发电厂i产生的有功和无功功率，Plinek，h表示在第h小时通过第k条传输线传输的功率，Plinemaxk是通过第i条线路传输最大可能的功率。

2）存储系统功率产出和消耗允许范围的限制条件为：

不难看出，寻找最佳的储能装置安装位置的计算量巨大。由于粒子群优化算法在解决多目标优化问题上具有很强的优势，本研究选择该算法通过迭代快速寻找最优解，解决最低成本下系统运行方案的求解和储能装置最优接入位置的计算问题。

2 基于带收缩因子的粒子群的目标函数求解

粒子群优化算法（particle swarm optimization，PSO）首先需要初始化一群随机的粒子（随机解），然后通过跟踪2个极值更新自己的位置和速度［20］。2个极值分别是个体最优值Pbest和全局最优值Gbest。粒子当前位置的优劣程度由适应度函数评估。通过式（10）和式（11）更新粒子的速度与位置，通过式（12）来评估当前位置的优劣。

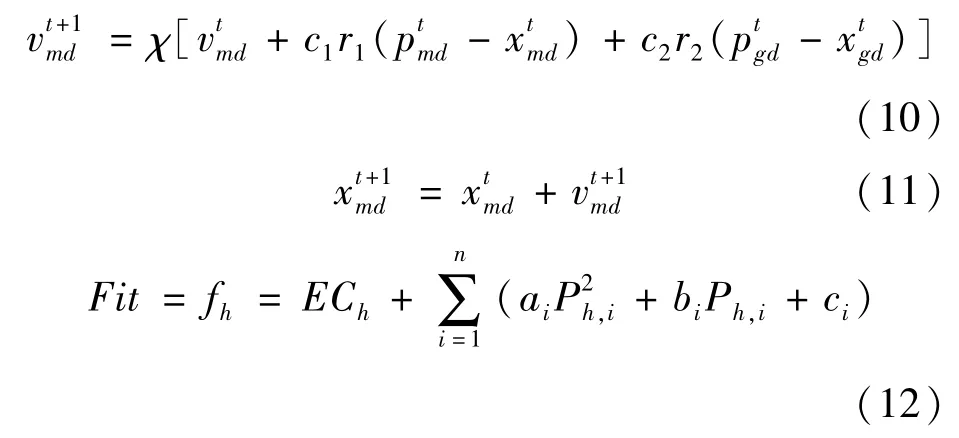
式中：t为迭代次数；d为维度；vtmd为第m个粒子在第t代的速度；为第m个粒子经过t次进化的位置；为第t代粒子当前的最优位置；r1、r2为［0，1］中的随机数；c1、c2为学习因子；χ为收缩因子。

对学习因子进行调整不仅可以保证粒子种群的多样性，还可以增强算法的全局搜索能力。本文采用一种线性调整学习因子的策略，按照式（13）和（14）先小后大，先大后小来调节。

式中：Tmax为设定的最大迭代次数：T为当前迭代次数。

收缩因子的引入不仅可以加速粒子寻优速度，而且可以保持粒子群算法局部和全局搜索能力的均衡性，其计算式为：

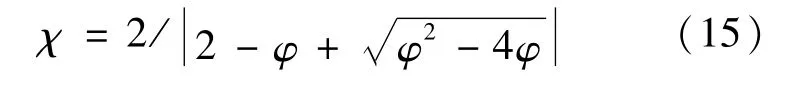
式中，φ值取4.1。

通过这2个更新机制，PSO可以迅速收敛到好的解决方案，同时该算法可避免过早收敛，导致它停滞在局部最优水平。

3 系统运行方案及储能装置接入位置求解

3.1 粒子群算法与集中储能装置分配问题的对应关系

3.2 无储能装置时系统最低运行成本求解

步骤1：设置系统参数以及粒子群算法的参数。

步骤2：在约束条件内随机产生将群体中每个粒子的速度和位置初始化为随机数，将个体的历史最佳位置Pbest定义为初始随机位置；群体最优的个体为当前的Gbest，计算个体历史最佳位置和群组最佳位置的适应度函数值。

步骤3：将粒子代入到牛顿-拉斐逊法中计算潮流值，并应用母线电压和输电线路潮流约束条件进行判决。

步骤4：用式（12）计算粒子的适应度值，更新Pbest和Gbest。

步骤5：判断是否达到给定的最大进化代数或小于潮流计算的最大允许误差，没有则转到步骤2，按式（10）（11）进行粒子的速度和位置更新，重新寻找最小成本；如果满足条件，则完成了单个小时发电成本最小化的求解过程。然后转到步骤1重新优化下一个小时发电成本最小化的计算过程。对应的流程如图1所示。

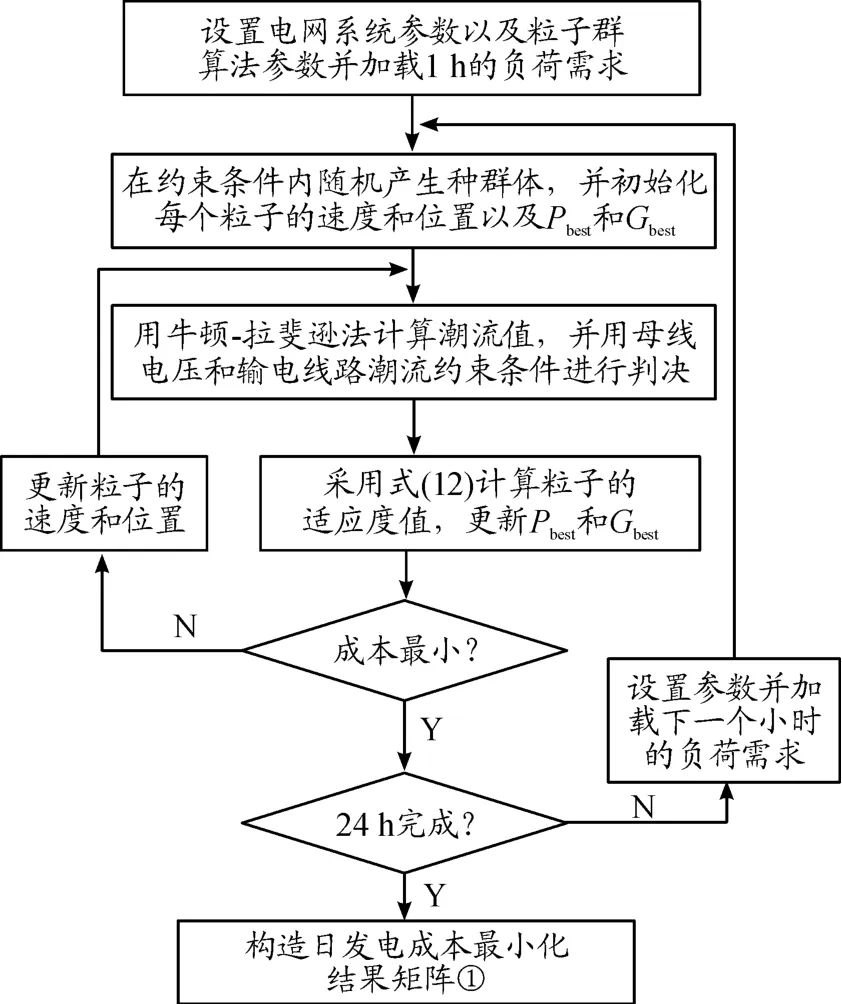
图1 无储能装置时最低运行成本计算流程框图

3.3 储能装置最佳接入位置求解

本节的目标是：在评估使用储能装置对发电成本影响的基础上，确定储能装置在网络中的最佳安装位置。

为此目的，初始种群的第一个粒子被认为等于3.2节中得到的粒子。在3.2节中获得的值对发电厂是有效和被储能装置发出的电/用掉的电在24 h内每小时都认为为零。初始粒子群的其他粒子在允许范围内随机产生，并加载原始网络数据，计算流程图如图2所示。

图2 储能装置的最佳安装位置计算流程框图

4 算例分析

选择IEEE-30母线系统为例进行仿真分析，如图3所示，该系统包括30个节点，41条支路，6个发电机节点，1～24 h的系统负荷如表1所示。

4.1 未接入储能装置时最低成本下发电厂运行状况

虽然发电厂的成本函数的指数每年都会随着基建与运营维护成本变化而改变，但由于本文着重研究储能装置接入系统对运行成本的影响，为了简化计算过程假设相应的发电机成本指数不变。系统中，各发电机的接入位置和发电成本函数系数如表2所示。

图3 IEEE-30节点系统示意图

表1 IEEE-30系统24 h对应的负荷

表2 IEEE-30系统中发电机成本函数系数及发电量

对系统24 h内每1 h的成本进行仿真，算法优化粒子数为200，经过100次的迭代，达到潮流计算精度为10-4时终止计算，得到储能装置未接入系统时各发电厂日发电成本的最低的运行数据及相应的系统损耗和成本如图4～图6所示。

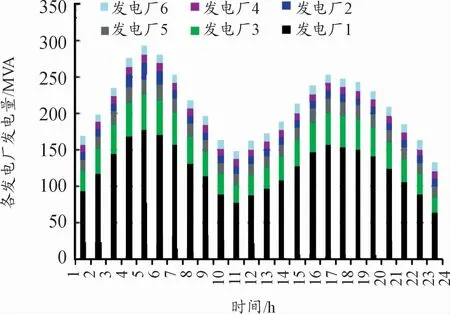
图4 24 h内各发电厂的发电量直方图

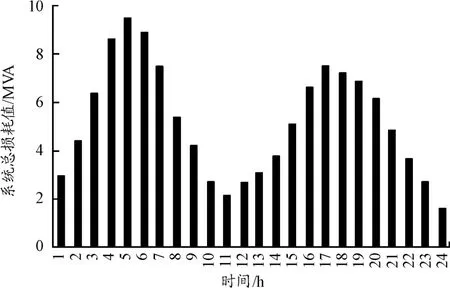
图5 系统每小时的总损耗值直方图

图6 系统每小时运行成本直方图

由图4可以看出，各发电机的发电量占每小时总发电量的比例在24 h内基本不变，发电厂的发电功率越大发电厂的发电总占比越高。由表3可得：发电厂1的发电量占比最高，其次是发电厂2，其余的发电厂的发电量占比较小。根据系统的总发电量和负荷可以得到系统损耗如图5所示，假设发电机的平均电度成本为100.4元/MVA，得到系统的运行成本如图6所示。由图5和图6可得发电量和系统损耗以及运行成本和负荷的变化成正相关。

表3 各发电机的发电量占比

4.2 储能装置的最佳接入位置

由于网络传输容量和传输损耗是决定储能装置最佳接入位置的主要因素，储能装置的运行效率不影响接入位置的计算。因此，假设储能装置的运行效率为100%，其全寿过程中的电度成本假设为0元/MVA。储能装置容量为在最长放电时间内对系统放电量的总和。分别计算接入每一条母线后系统运行的总成本，选择接入后系统整体成本最低的母线作为最佳位置。

通过仿真计算得到储能装置接入各母线后系统运行成本降低最明显的6个母线的比例，如表4所示。

表4 储能装置接入母线后系统运行成本的降低比例

由表4可得，储能装置接入BUS6母线时，系统整体运行成本下降最多为2.994%。所以，储能装置最佳的接入位置为BUS6。

5 结论

本文以达到系统最低运行成本为目标，构建计及储能装置的电网运行成本函数和约束条件，选择压缩因子粒子群优化算法，在IEEE-30节点系统中，计算各发电厂24 h内每小时的发电量和对应的发电成本及总损耗值，得到系统最低成本时各发电厂运行方案。结果显示，要得到系统运行的最低成本，各发电厂每小时的发电占比基本不变，发电厂1和2的发电量占比较大，分别为55.2%、16.9%。

在该运行方案的基础上再利用粒子群优化算法分别计算储能装置接入各母线后系统运行成本的变化情况，得到储能装置接入BUS6总线后系统运行的成本降低最多，即BUS6总线为储能装置的最佳接入位置。下一步的研究可在此基础上引入更客观的发电成本函数，综合考虑系统的拓扑结构和运行方式，进一步优化系统运行方案和储能装置的配置。