具有人传人的登革热传染病模型的动力学分析

周 瑶，吕贵臣

（重庆理工大学 理学院，重庆 400054）

近年来，登革热作为一种典型的媒介传染病，经常在热带及亚热带国家肆虐，给人们带来经济上的损失和生活上的不便［1-2］。登革热是由登革病毒引起的急性传染病，主要通过伊蚊叮咬传播给人类。感染登革病毒之后可导致患者出现不同的临床表现，轻者表现为隐性感染，重者可能发生致命的登革出血热（DHF）及登革休克综合征（DSS）。随着疾病流行地区的不断扩大，登革热已从过去的散发性疾病演变为全球性公共卫生问题，对人类健康造成严重威胁，在全球范围内的发病率不断增加［3］。如何更好地模拟登革热病毒的传播机理并提供有效控制措施去抑制病毒的传播，已经引起了学者们关注。

最近几十年来，利用数学模型研究登革热病毒的传播特征具有广阔的应用前景［4］。1998年，Esteva等［5］建立了关于登革热传播过程的经典数学模型，随后他们进一步改进了模型，分别考虑了人类种群变化［6］和病毒可在蚊虫中垂直传播［7］的数学模型。此后，基于他们的模型，研究者们对登革热病毒传播过程进行更为细致的刻画，建立了一系列更复杂且切合实际的数学模型［8-10］。根据相关报道，虽然登革热病毒主要通过媒介传播到人类身上，但是没有明显证据可以排除病毒通过输血或骨髓移植等方式由感染者直接传给易感者的可能性［11］。Martcheva等［12］考虑上述因素后建立了一类包含媒介传染病可在人类中不经媒介而直接进行传播的数学模型。鉴于在非洲和东南亚的一些疾病较为流行的热带地区医疗条件不理想，在某些极端情况下，登革热病毒可能直接发生有限的人际传播。因此本文考虑一类人类种群规模变化、病毒可在人群中不经蚊虫而发生人际传播且疾病可致患者死亡的数学模型是合适的。

1 模型建立

将研究对象聚焦于人和蚊虫，并对Esteva等［2］的模型进行推广。根据种群患病和易感状态，将人类种群分为3类，蚊虫分为2类。设SH、IH、RH分别为t时刻人类中易感者、感染者和移出者的数量；SV、IV分别表示t时刻易感蚊子和感染蚊子的数量。再令NH=SH+IH+RH和NV=SV+IV分别为t时刻人类和蚊虫的总数量。考虑到蚊虫的生命周期极短，其一旦染病，将终生不能恢复，故不考虑蚊子的移出者类。假设在单位时间内患病人类接触易感人类和易感蚊子的数量有限，从而考虑病毒以标准发生率进行传播；另外假设患病蚊子传染易感人类的能力与环境内总人口数成正比，故考虑病毒以双线性发生率进行传播。基于以上假设和登革热病毒的传播特性，可知该病在各仓室之间的传播流程见图1。

图1中，β1SHIV表示单位时间内易感人类被患病蚊子所感染的人数表示易感人类和患病人类通过输血等方式传播病毒，在单位时间内新增的患病人数为单位时间内易感蚊子叮咬患病人类之后受到感染的蚊虫数量。另外，考虑到模型的实际生物学意义和登革热病毒发生人际传播的有限性，对相关参数作出如下假设：α＞dH和dH≥β2。

基于传播流程（图1），可以写出登革热病毒传播的微分方程模型如下：

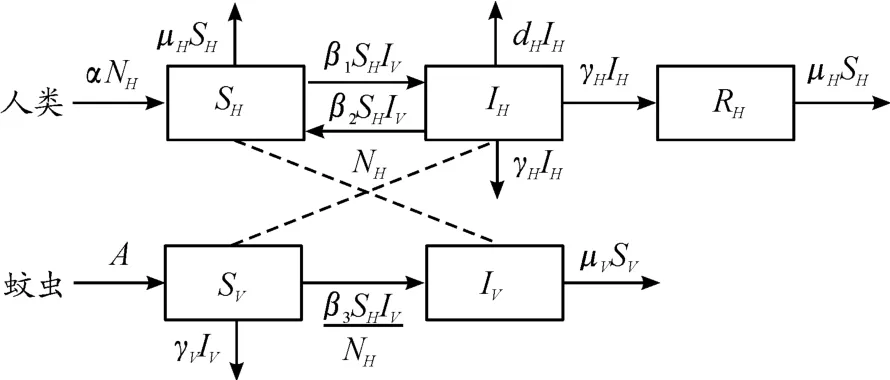
图1 登革热病毒在人和蚊虫之间的传播流程框图

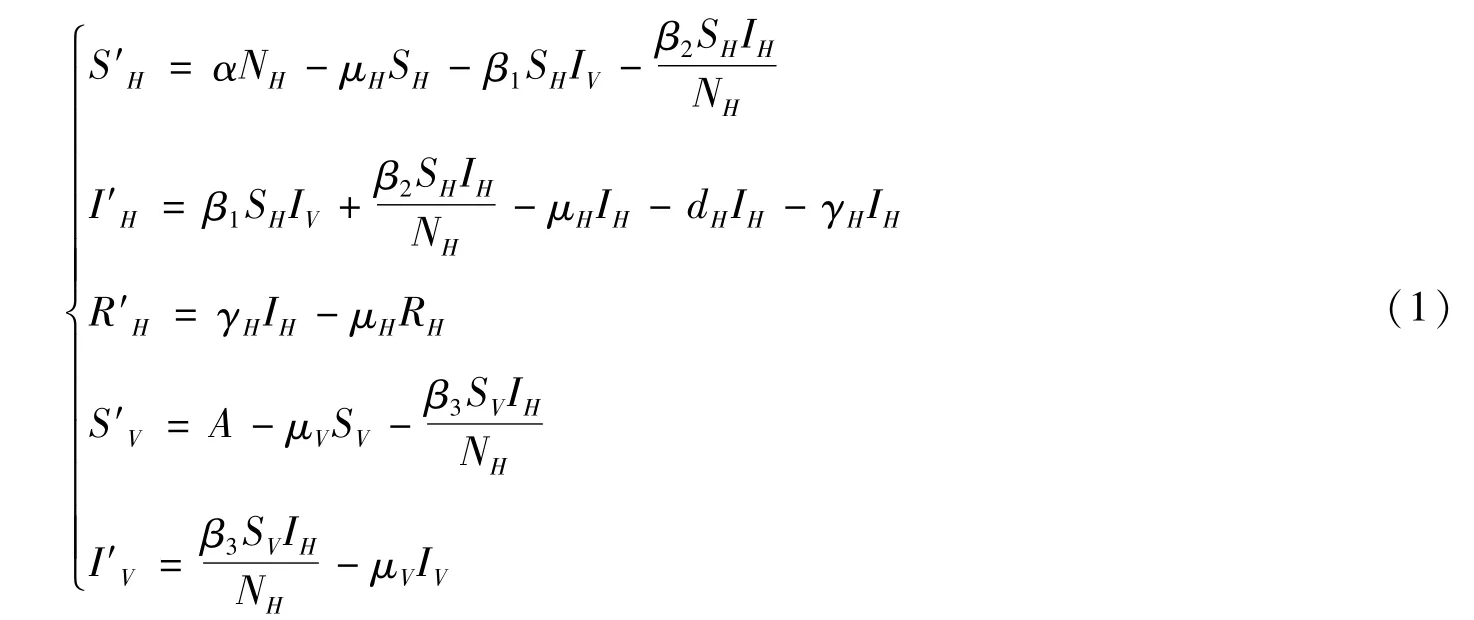
模型中所涉及参数的具体意义见表1，其中所有参数都是非负的。

表1 模型（1）中相关参数

根据模型（1）前3个方程，可以得到人类种群满足N′H=S′H+I′H+R′H=（α-μH）NH-dHIH。由后2个方程得到蚊虫满足N′V=S′V+I′V=A-μVNV。另外，容易证明。因此，考虑在的区域中对模型进行动力学分析。为便于后续分析，令

结合x+y=1，系统（1）经过上述尺度变换化为如下系统

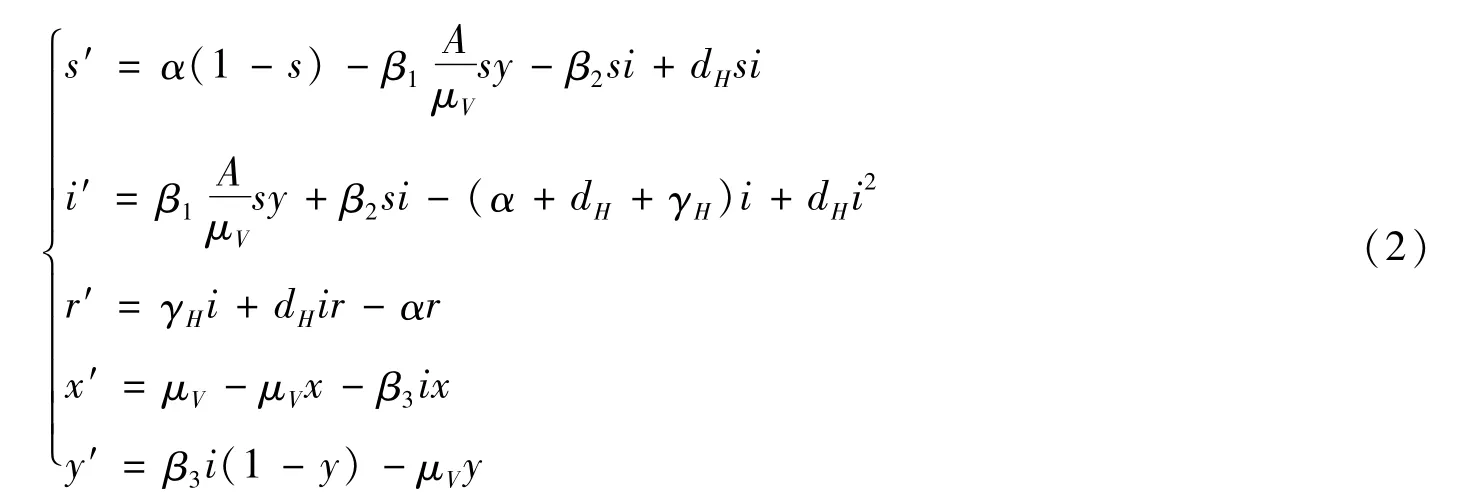
结合尺度变换，定义系统（2）的可行域为Σ=｛（s，i，r，x，y）∈R5+|0≤s+i+r≤1，0≤x+y≤1｝。

2 平衡点的存在性和稳定性

由于系统（2）中的第1、2、5个方程中均不含r和x，于是考虑分析降维后的系统动力学行为。降维后的3维系统为

考虑到模型的实际生物学意义，在Ω=｛（s，i，y）∈R3+|0≤y≤1，0≤s，0≤i，s+i≤1｝中讨论系统（3）的解的性态，易证明Ω是系统（3）的正向不变集。

根据基本再生数R0的下一代矩阵计算方法［13］，模型（3）可写为如下形式：

式中：h=（h1，h2）=（i，y）；p=s；Fj（h，p）表示染病仓室j的新患病感染率；Vj（h，p）表示染病仓室j中剩余的转移项（如出生率、死亡率、治愈率等）。此时

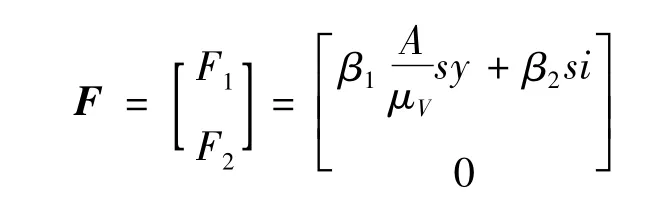
和

由Martcheva的计算公式［13］，基本再生数与无病平衡点有关。易知，模型（4）总有唯一无病平衡点P0=（0，0，1）。根据文献［13］的计算公式，可得

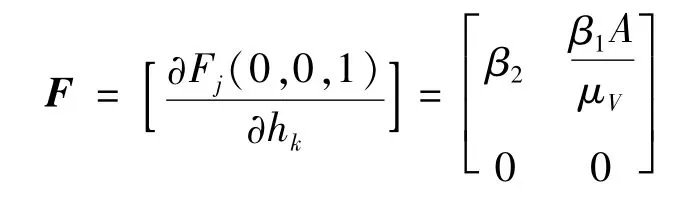
和

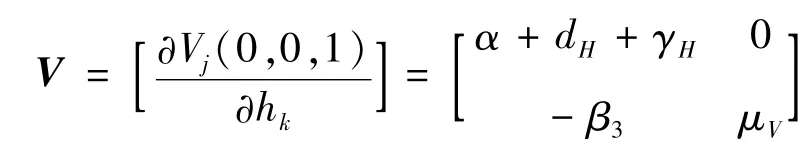
进一步，得到

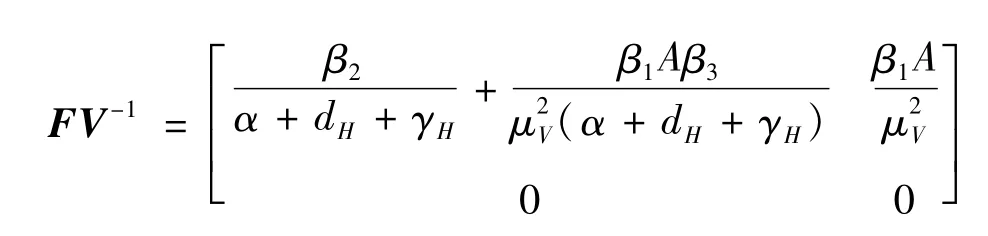
因此

2.1 平衡点的存在性

本节讨论系统平衡点的存在性。

定理1系统（3）的无病平衡点P0=（1，0，0）始终存在。

证明：根据系统（3），无病平衡点必然满足以下关系

代入i=0到上面等式中，得到s=1和y=0，因此无病平衡点P0始终存在。

定理2当R0＞1时，系统（3）存在唯一的地方病平衡点Pe。

证明：由三维系统的第1、3个方程，地方病平衡点必然满足以下关系

由于平衡点应被限制在可行域Ω内，满足上面等式的地方病平衡点也应满足下面的不等式：

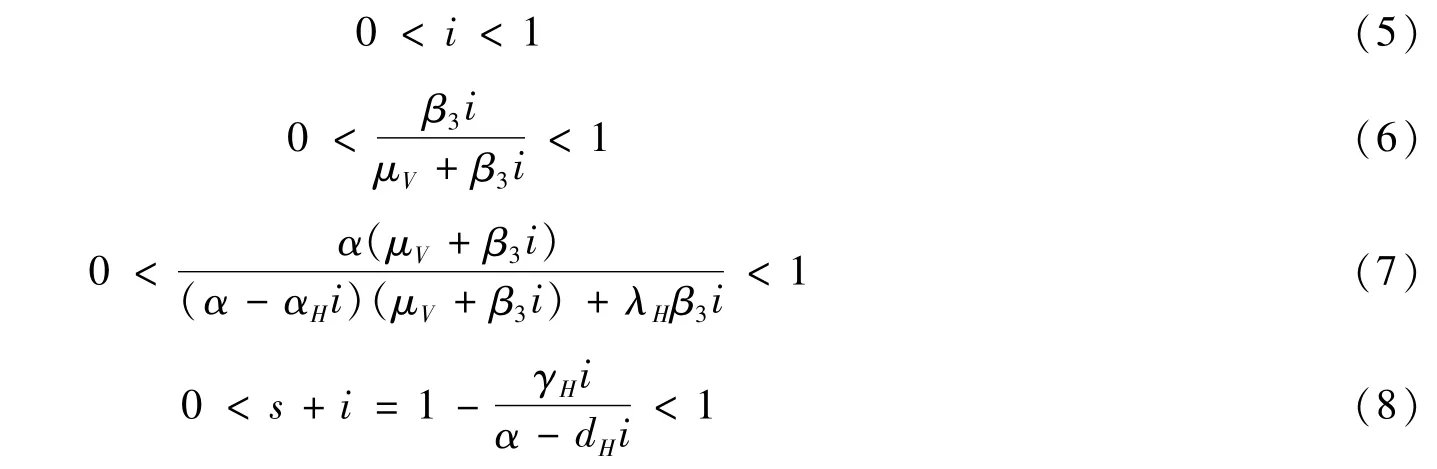
为了分析g（i）的根的存在区间，根据αH的正负情况分别进行讨论。

Case 1：αH＞0（dH＞β2）

前面有假设α＞dH（α＞αH=dH-β2），式（5）和（6）显然成立；当0＜i＜1且时，式（7）成立；当0＜i＜1且时，式（8）成立。

进一步，为了得到满足上面4个不等式关系的i，需要找到g（i）在区间（0，i1）上的根，其中

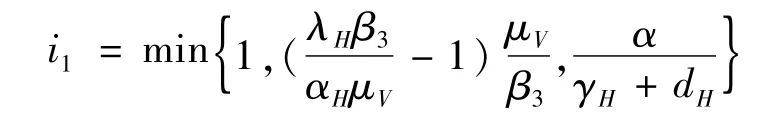
其中：U=β2α（μV+β3i），V=αβ3i-αHβ3i2，W=（λHβ3-αHμV）i。

显然U、V、W均为正数。

接下来对i1可能存在的3种情况分别计算与讨论：

1）当i1=1时

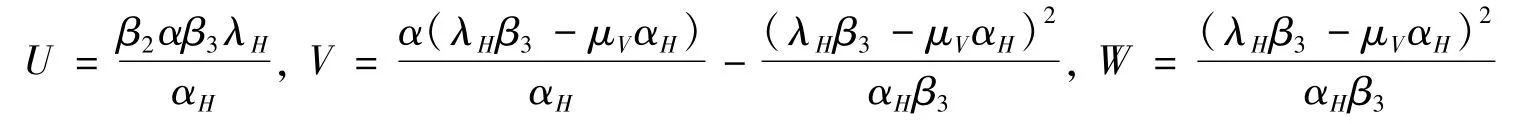
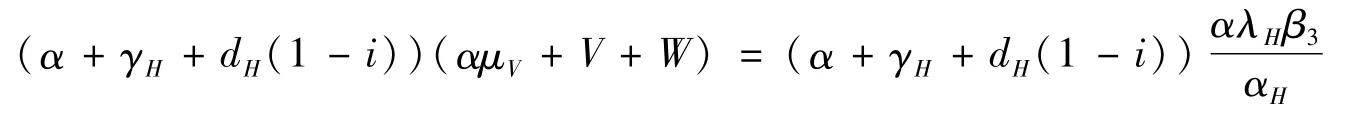
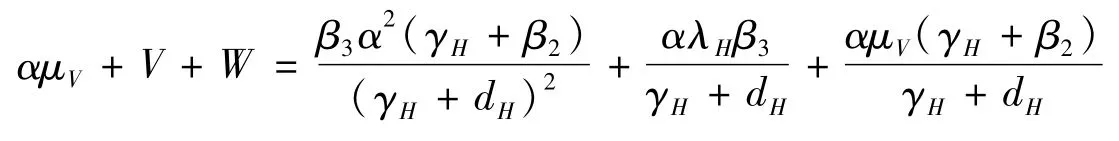
由于（α+γH+dH（1-i））（αμV+V+W）＞λHαβ3+U，故

因此，由1）～3）可得，g（i1）＜0。

此外，容易得到g（i）取得局部最大值时i为

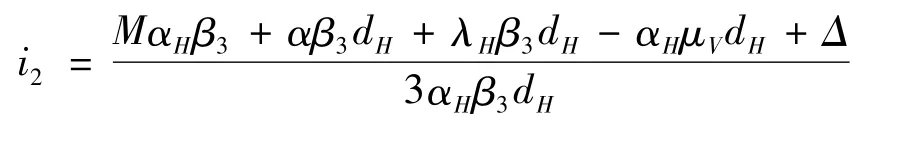
其中

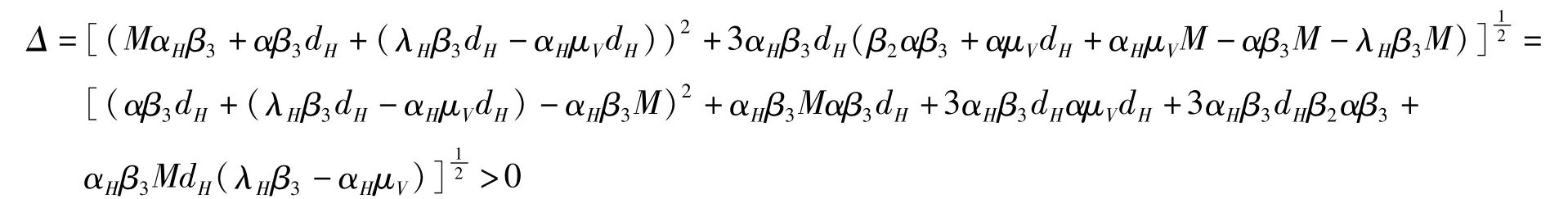
由上面不等式得到

因此g（i）的最大值在区间［0，i1］右侧取得。由于g（i1）＜0，当且仅当g（0）＞0才能使得g（i）有唯一的1个根i*∈（0，i1）。由于

综上，只有当R0＞1时，g（i）有唯一的正根i*∈（0，i1），显然原系统（2）此时也只有唯一的正根i∈（0，1），系统正平衡点的唯一性得证。

Case 2：αH=0（dH=β2）

同Case 1做法类似，代入αH=0到g（i）的表达式中，此时有

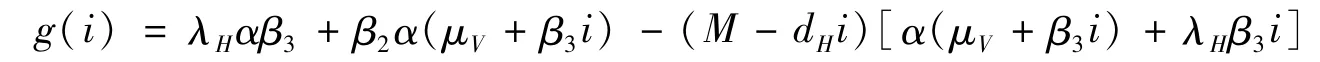
以及

经过简单计算，可得到g（i3）=g（1）＜0以及。进一步分析，显然只有当g（0）=αμVM（R0-1）＞0时，g（i）在区间（0，i3）范围才会存在唯一的正根。即当R0＞1时，系统存在唯一的正根i∈（0，1），系统正平衡点的唯一性得证。

2.2 无病平衡点的稳定性

定理1已经证明系统（3）始终存在1个无病平衡点P0（1，0，0），下面给出它的稳定性。

2.2.1 局部稳定性

定理3当R0＜1时，系统（3）的无病平衡点P0局部渐近稳定。

证明：求出系统（3）在P0处的雅可比矩阵为

显然系统（9）有1个特征值为λ1=-α，设其另2个特征值分别为λ2、λ3，且满足

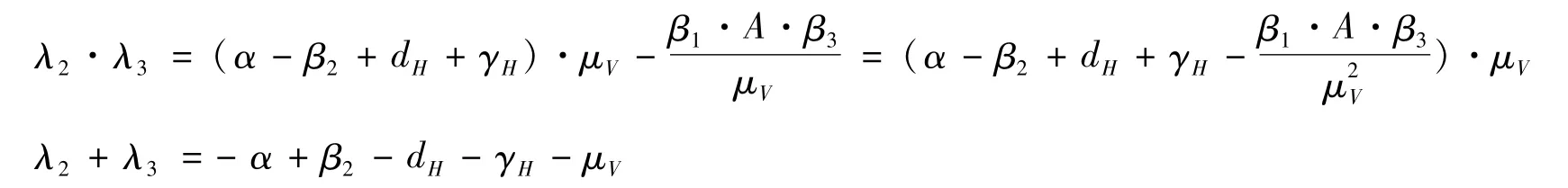
R0＜1时，有，故

因此λ2+λ3＜0显然成立。此外，再结合，可得λ2·λ3＞0。显然，特征根λ2，λ3都具有负实部。综上，P0的雅可比矩阵的特征值全部具有负实部，于是P0是局部渐近稳定的。

2.2.2 全局稳定性

定理4当R0＜1时，系统（3）的无病平衡点P0全局渐近稳定。

证明：构造Lyapunov函数，令

对L沿着t求全导数，可化简为

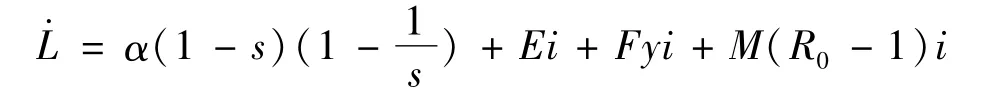
其中E、F、M分别为

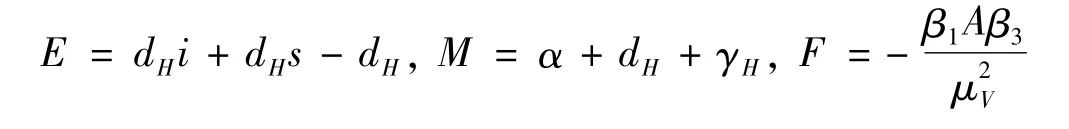
显然满足E≤0，F＜0。因此，当R0≤1时，。易证系统（3）在集合上的最大不变集为单点集 {P }0。根据LaSalle不变集原理，当R0≤1时，P0全局渐近稳定。

2.3 地方病平衡点的稳定性

为证明地方病平衡点的稳定性，需要用到合作系统相关理论，下面给先出合作系统定义。

定义1考虑一般的n维系统：

其中f∶Rn→Rn是一个连续可微的映射，且有x=（x1，x2，…，xn）∈Rn，其过初值x（0）=x0的解记作x（t，x0）。如果其雅可比矩阵Df（x）的非对角线上元素均为非负，即对所有的i≠j（i，j=1，…，n），当x∈Rn+时，有。则系统（10）称为合作系统。另外，若其雅可比矩阵Df（x）为不可约矩阵，则称系统（10）为不可约系统。

根据合作系统定义，可得如下定理：

定理5系统（2）为Σ上的合作不可约系统。

证明：根据s+i+r=1和x+y=1可以得到y=1-x，i=1-s-r。将其代入系统（2）的第1个方程和第4个方程之后，得到系统（2）的雅可比矩阵为

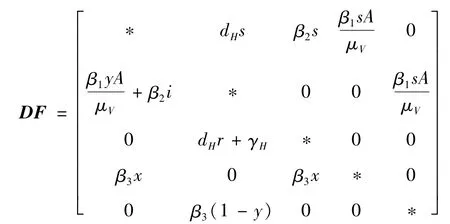
其中主对角线元素用*表示。显然，上述雅可比矩阵的非对角线元素均为非负，根据合作系统的定义，系统（2）为合作系统。容易证明其雅可比矩阵DF为不可约矩阵，因此系统（2）为不可约系统。

2.3.1 系统（3）的持久性

为证明系统地方病平衡点的全局稳定性，先证明系统的持久性。

定理6当R0＞1时，系统（3）在Ω内一致持久，即存在c1、c2、c3＞0使得系统（3）的任意解（s，i，y）满足

证明：根据Freedman在文献［14］中的定理4.3，令X=R3+，X1=Ω，X1是系统（3）的闭正向不变子集。为便于后续证明，记u（t）=（s，i，y）是系统（3）的解，，和M∂=｛u（0）∈∂X1|u（t）∈∂X1｝，=｛（s，0，0）∈∂X1|0≤s≤1｝。显然，系统在边界上的最大闭不变子集N是单点集P0。欲证是相对开集，可以取X=R，Y=Ω，V=｛（s，i，y）|-1＜s＜1，i＞0，y＞0｝，从而，即证。

下用反证法证明

假设

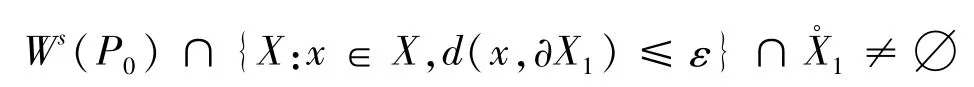
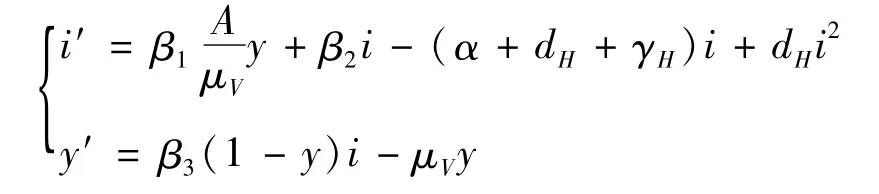
易知（11）是（3）后2个方程的极限系统，则t→∞时，i（t）→0，y（t）→0。

由于R0＞1，得到

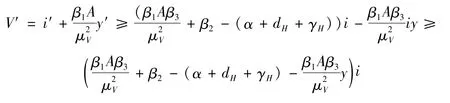
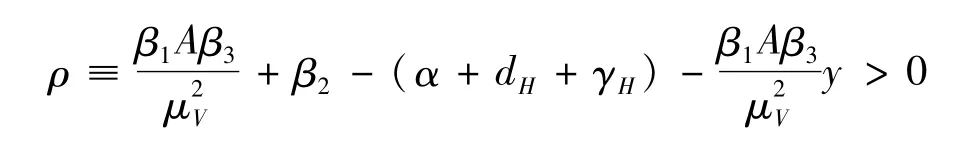
因此

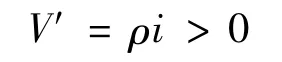
根据极限系统理论，这与t→∞时，s（t）→1，i（t）→0，y（t）→0矛盾，故系统（3）是一致持久的。

2.3.2 全局稳定性

定理7当R0＞1时，系统（3）的地方病平衡点Pe全局渐近稳定。

证明：由定理6可知，系统（2）是一致持久的，又因为系统（2）合作不可约，根据Jiang［15］的定理C可知系统（2）的唯一地方病平衡点是全局渐近稳定的，从而得到系统（3）的唯一地方病平衡点是全局渐近稳定的。

3 数值模拟

运用数值模拟的方法对3维系统平衡点的动力学性质进行分析，模拟中参数取值：α=0.02，A=7 000，μH=0.000 023，dH=0.001 24，μV=0.014 5，γH=0.001 67，β1=0.000 012，β2=0.000 000 1，β3=0.000 534。经过计算得到地方病平衡点为pe=（0.106，0.822，0.029），阈值参数为R0=9.312 36＞1，对地方病平衡点的全局稳定性进行模拟。然后分别取4组初值为（0.3，0.2，0.25），（0.35，0.25，0.28），（0.15，0.34，0.17），（0.23，0.17，0.38）并得到系统的解曲线如图2所示。

图2 R0＞1时，地方病平衡点的全局稳定性曲线

模拟图显示当t→+∞时，系统的解曲线趋于地方病平衡点pe，从而对前面的理论证明给出了很好的数值验证。

4 结论

以登革热病毒在人群和蚊虫之间的传播机理建立动力学模型，还考虑了人际传播对模型的影响，得到模型的阈值并分析了平衡点的稳定性。分析表明该传播模型的无病平衡点和地方病平衡点均表示全局渐近稳定。最后通过数值模拟进一步验证了地方病平衡点的全局稳定性。