带有记忆项非线性Berger型方程的长时间动力学行为分析

刘琳琳，李正波，范小明

（西南交通大学 数学学院，成都 611756）

飞机在高空高速飞行过程中，机身表面常常会遇到不稳定气流从而产生非线性振动。Berger型方程就是描述这类问题的偏微分方程。对于Berger型方程的研究，之前的探索主要关注于带有强阻尼g（ut）项的Berger型方程［1-7］，而对带有弱阻尼的Berger型方程则涉及较少［8-14］。Jorge等［14］研究了r阶延展项并且带有强阻尼g（ut）的Berger型方程，证明了全局吸引子的存在性。Potomkin［8］研究了带有记忆项并且延展项为2阶的Berger型方程的长时间动力学行为，在此基础上［8，14］，提出了带有弱阻尼记忆项以及r阶延展项的Berger型方程：

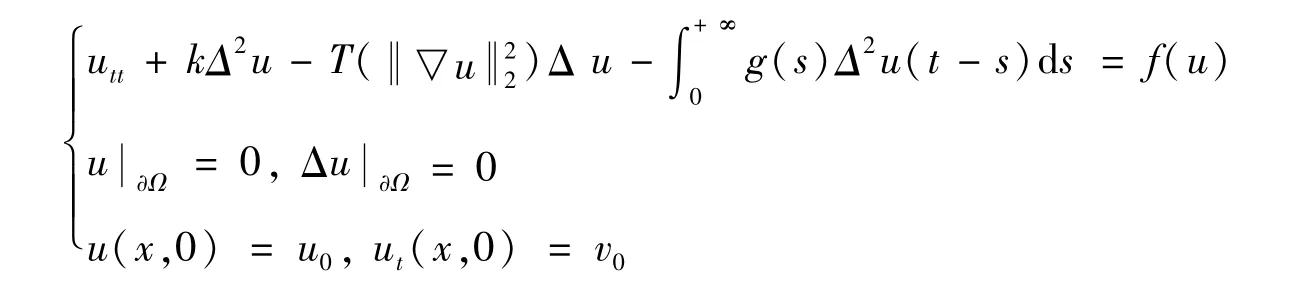
其中延展项T（·），非线性源项f（u）分别为

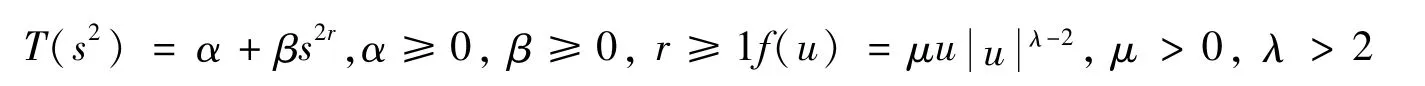
式中：Ω是R3中边界充分光滑的有界领域，函数u（x，t）表示金属板在x位置、t时刻的扰度。函数T（·）用于描述板面的伸缩程度，其中α与板平面上的压力值成正比，函数g（s）表示记忆内核。同时这里的边界条件意味着板的边缘是绞接的。

利用文献［13］中的方法引入新变量将非自治动力系统转化为自治动力系统，通过令v=ut将方程变成一阶的微分方程，再运用半群方法证明了带记忆项的Berger型方程的解是适定的，可以生成一个动力系统。将改进能量函数定义为Φ函数，证明了Φ函数是一个严格的Lyapunov函数，从而得到Berger型动力系统是一个梯度系统。不再沿用传统方法只关注单个轨道，而是借助研究2个轨道差的方法，证明了带有记忆项的Berger型动力系统在每个正向不变有界集上是拟稳定的，也就得到了动力系统是渐近光滑的。再根据文献［15］中定理7.5.9，证明了所研究的带记忆项的Berger型动力系统具有紧的全局吸引子A。在此基础上进一步证明了Berger系统的全局吸引子的分形维数是有限的。同时，应用插值理论还证明了在拓展相空间中动力系统具有有限维的广义指数吸引子。

1 预备知识

1.1 基本概念、引理

定义1［15］如果X上的有界闭集A满足：

1）对于任意t≥0，A为不变集（任意的t≥0，StA=A成立）。

2）A具有一致吸引性；对于X上全部有界集E满足

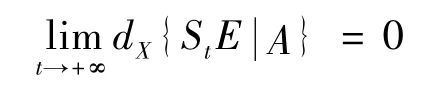
定义2［15］令Z⊆X是动力系统（X，St）上的正向不变集：

1）若Φ（z）是Z一个的连续函数，如果任意的z∈Z，t→Φ（Stz）为非增函数。

2）任意t＞0，若某些z∈Z，满足Φ（Stz）=Φ（z）能推出Stz=z，并且z为（X，St）的平衡解，则Φ（z）为严格的Lyapunov函数。

3）若在全空间X上动力系统（X，St）具有严格的Lyapunov函数，则动力系统（X，St）为一个梯度系统。

定义3［15］若nA（·）满足：

则nA（·）是空间A上的一个半范数。如果对于所有的aj⊂A，若成立，有则nA（·）是一个紧的半范数。

定义4［15］nA（·）是A中紧的半范数，以及非负函数i（t），j（t），k（t）使得以下条件成立：

1）函数i（t），j（t），k（t）在［0，∞）区间局部有界。

2）j（t）∈L1（R+）并且limt→∞j（t）=0。

3）对于任意Z1，Z2∈B，满足

那么（F，St）在集合B（B⊂F）上具有拟稳定性。

引理1［12］若F为Banach空间，算子L为m-增生算子，对于任意的z0∈D（A）方程：

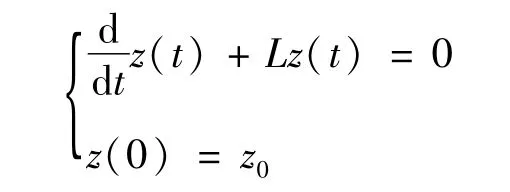
存在唯一的经典解z使得：z∈C（［0，+∞），D（L））∩C1（［0，∞），F）成立。

引理2［15］若F为一个Banach空间，若动力系统（F，St）在F上的任意正向不变有界集中具有拟稳定性质，那么（F，St）为一个渐近光滑动力系统。

引理3［15］若动力系统（F，St）为Banach空间F上渐近光滑的梯度系统，Φ（z）是定义在F上的Lyapunov函数。若有以下条件成立：

1）Φ（z）在F中的任意有界子集上有界。

2）对于任何的R＞0，ΦR（z：Φ（z）≤R）有界。

3）动力系统（F，St）的不动点集N有界。则（F，St）有紧的全局吸引子。

1.2 基本假设与工作空间

因为方程中带有记忆项，所以动力系统是非自治的。因此需要通过引入新变量［8，13］把非自治的系统变成自治的系统。令

其中θt（x，0）=0，x∈Ω，t＞0初值为θ0（s）=θ0（s）且θ0（x，s）=u0（0）-u0（s）。

记忆项u满足：ut=θt+θs。设有：

为计算方便取：l0=1-k，得到如下自治动力系统：

其中：

初值条件为

边值条件为

下面给出方程中各项的假设。

（A1）非线性源项f（u）的定义与假设f（0）=0，当n≥3时

并且存在一个常数Cf＞0，使得

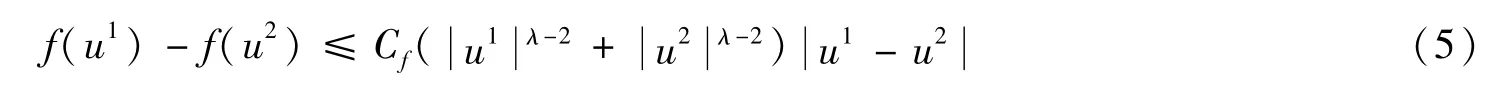
其中若λ∈［2，3］，Cf=1；λ＞3，。令是一个R→R的非负C2函数，满足

（A2）可伸缩项T（s2）定义与假设：令

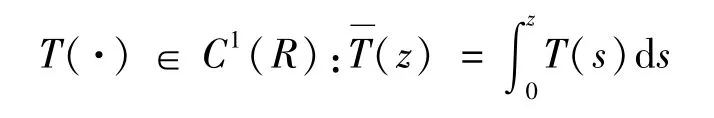
（A3）记忆内核g（s）的定义与假设：令g（s）是C1（R+）中的非负函数，满足

并且存在一个正常数ρ＞0，满足：

下面给出工作空间的定义：

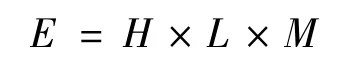
其中H=H2（Ω）∩H10（Ω），L=L2（Ω），关于变量θ的加权空间M为

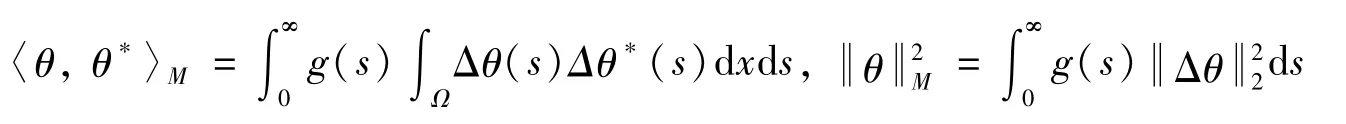
1.3 能量不等式

为了证明方程解的适定性问题以及动力系统具有的梯度性质，给出方程组（2）～（4）的能量函数及其估计。能量函数的定义如下：

修正能量函数为

注：这个修正的能量函数就是后面证明中定义的Φ函数。

引理4对于任意的t＞0，存在一个正常数K＞0，使得下面能量不等式成立：

证明：令

由于H10（Ω）紧嵌入到Lλ（Ω）有

所以

其中c（Ω）是Sobolev嵌入常数。

盖碗茶具的出现与饮茶习俗的变化发展密不可分，是在中国古代茶具积淀之上形成的，符合中国茶事美学与实用的茶具。如今，仍以其独特的人文属性及灵活可变的功能形制，在现代茶事活动中成为不可或缺的一类茶具。在茶文化大发展的时代背景下进行概念厘清及发展梳理，具有非常重要的现实意义。

因此有：

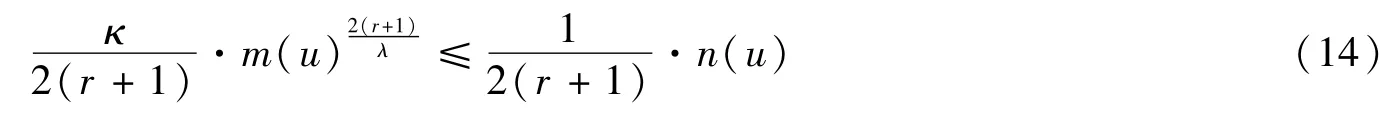
由式（14）

下面分两种情况讨论能量不等式：

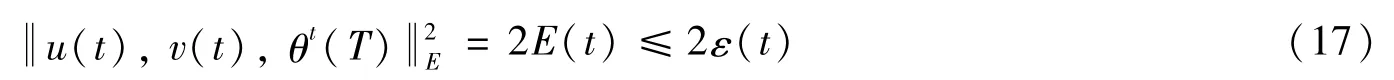
2 Berger系统解的适定性

运用半群理论证明方程（2）～（4）的解是适定的，下面借助算子表达记忆项。令Gθ=-θs，θ∈D（G），因此θt=Gθ+ut，θ（0）=0。对于任意的θ∈D（G），可知：

在平移半群中，D（G）=｛θ∈M|θs∈M｝为无穷小生成元。下面通过做变换将方程（2）～（4）变为抽象的柯西问题。引入新变量：v=ut将方程变换成1阶演化方程：

U（t）=（u（t），v（t），θ）∈E是方程（20）的解。其中：

并且

引理5L为m增生算子。

证明：由可知算子L是一个单调算子。下面证明算子L是极大算子：给定p*=（u*，v*，θ*）∈E，存在z∈D（L），使得z-Lz=p*成立。那么有

在式（23）中对s积分，同时θ（0）=0，有

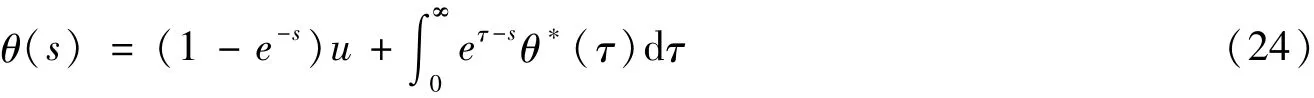
把式（24）代入式（22）并加上式（21）继续进行变换则可以写成：

其中：

由式（25）给出双线性形式B∶（H20（Ω））×L2（Ω）→R的定义：

因此双线性B具有连续性和强制性。由Lax-Milgram定理可证明方程（25）存在唯一的弱解v∈H20（Ω）。下面证明θ∈M，θs∈M：由式23）并结合θ（x，0）=0，有

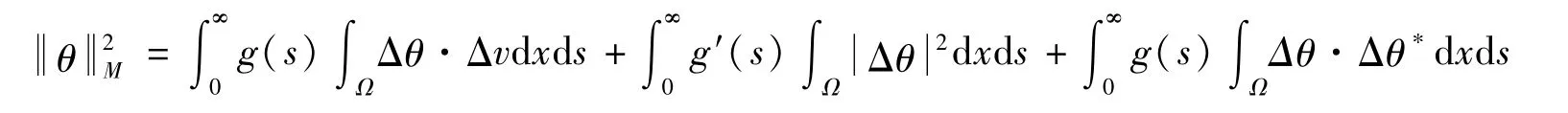
根据记忆内核的假设以及young不等式可知

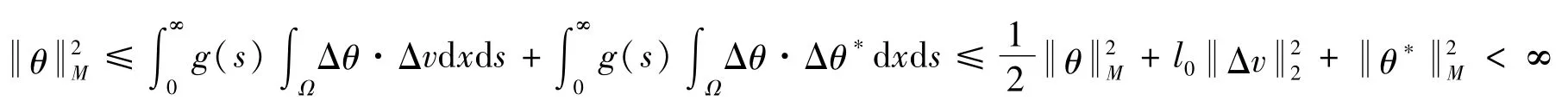
θ∈M得证。根据式（23）有

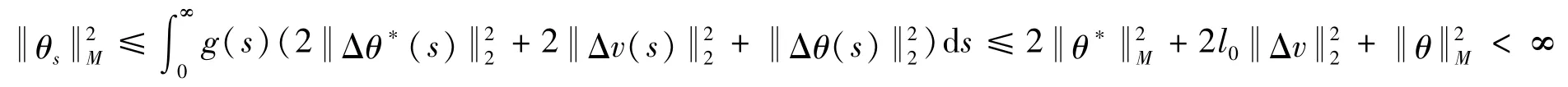
可以证明θs∈M。综上z∈D（L）为z-Lz=p*的解，引理5得证。

引理6算子F于E中具有局部Lipschitz连续性。

证明：令D⊂E，且D是一个有界集.Ui=（ui，vi，θi）∈D（i=1，2）。

其中

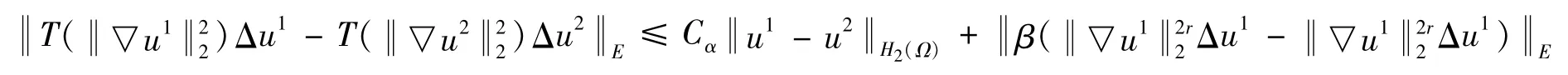
由拉格朗日中值定理：

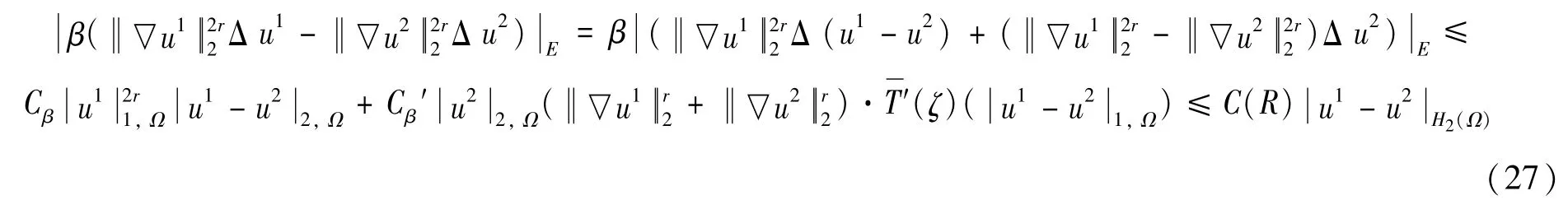
结合式（26）（27）有：

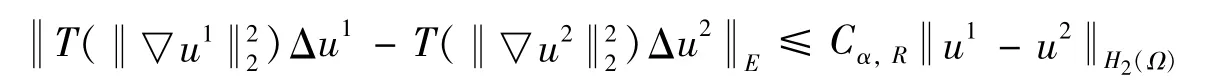
由非线性源项的假设式（5）可知：

定理1若（A1）～（A3）成立，对任何z0∈E，问题（2）～（4）具有唯一的柔和解z∈C（0，T；E），z（0）=z0，T＞0，使得：

并且解对初值具有连续依赖性，若z0∈D（L），能得到强解。

证明：（反证法）假设问题（2）～（4）的解不是整体存在的。根据引理1、引理5和引理6可知方程，具有唯一的柔和解。由引理6，方程（20）在［0，T］中存在唯一的局部柔和解。假设tmax＜∞，有

不妨令z（t）是关于初值z0∈D（L）的柔和解。又因为z（t）为强解，根据能量不等式，对于任意的t≥0有：

根据稠密性定理，柔和解也满足式（30），这与式（29）产生矛盾，所以假设不成立。当tmax=∞时，z（t）为1个整体解。下面证明柔和解对初值具有连续依赖：

对于任意的T≥0，任意的t∈［0，T］，假设z1（t）和z2（t）分别为关于初值z1（0）和z2（0）的柔和解。因此满足：

由能量不等式以及引理6有：

由Gronwall不等式有：CT是与初值有关的常数，解对初值的连续依赖性得证。即证D（L）中的柔和解Z0为一个强解，因此证明了方程（20）解的适定性。

定义算子族：{S }tt≥0：E→E。根据定理1，假设z（t）为方程（20）的解有：

这样得到1个在E中具有局部Lipschitz性质的C0半群，那么研究动力系统（E，St）的相关性质，即可得到方程（20）的相关动力学性质。

3 Berger系统的全局吸引子

3.1 梯度性质

定义：

引理7Φ为E上的严格Lyapunov函数，动力系统（E，St）具有梯度性质。

证明：假设Y⊂E是动力系统上（E，St）一个正向不变集。任意y=（u0，0，0）∈Y，Sty=（u（t），v（t），θt），根据式（6）有：

所以对于任意的y∈E，t→Φ（Sty）是不增的。令y=（u0，0，0）∈E，若对于所有Φ（Sty）=Φ（y）都成立，则：由式（31）可知：

对于任意的x∈Ω，θt（x，s）=0又由于θt=Gθ+ut，有ut（x，t）=0因此对于所有的t≥0，有：u（t）=u0则Sty=y=（u0，0，0）是动力系统的平衡解。

引理8方程（2）～（4）的平衡集N为有界集。

证明：令U=（u，0，0）是（E，St）上的一个平衡解，满足：

将式（32）与u在Ω上做内积得到：

其中C（Ω）为嵌入常数，因此：

则

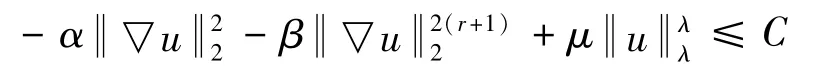
引理9动力系统（E，St）的Lyapunov函数Φ（x）在E的任意有界子集上为有界的；对于任何R＞0，集合ΦR={ x：Φ（x）≤R} 为有界集。

证明：因为Φ（U（t））=ε（t），所以Φ在E上任意有界子集为有界的。由能量不等式可知：

3.2 渐近光滑与拟稳定

引理10若（A1）～（A3）成立，给定集合B⊂E是正向有界不变集。在问题（2）～（4）中：令z1=（u1（t），v1（t），θ1t）为关于初值z10的弱解，z2=（u2（t），v2（t），θ2t）为关于z20的弱解，则有常数γ，b0＞0，和取决于B的常数CB＞0，有：

其中ω（t）=u1（t）-u2（t）。

证明：令θ～=θ1t-θ2t，则（ω，ωt，）是下面问题的一个弱解。

其中F（u）=f（u1）-f（u2），引理10主要分5步来证明。

步骤1令

将式（36）乘以ωt在Ω上积分得到：

做变形

由Young不等式及Hölder不等式有：

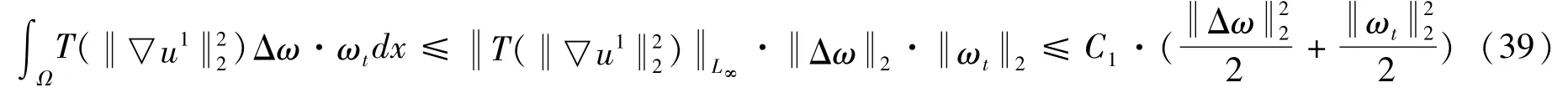
由Gagliardo-Nirenberg插值不等式有：

由Hölder不等式以及拉格朗日中值定理：

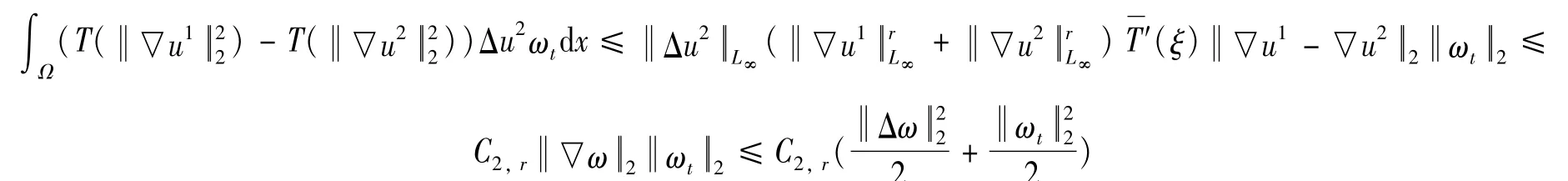
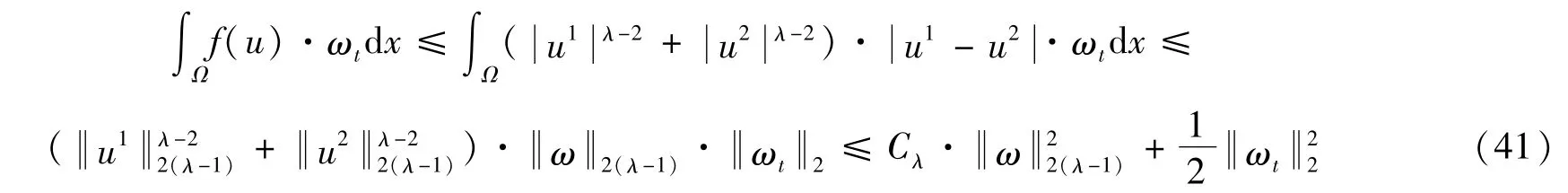
因此得到关于E′ω（t）的估计：

步骤2令φ1（t）=（ω，ωt）Ω

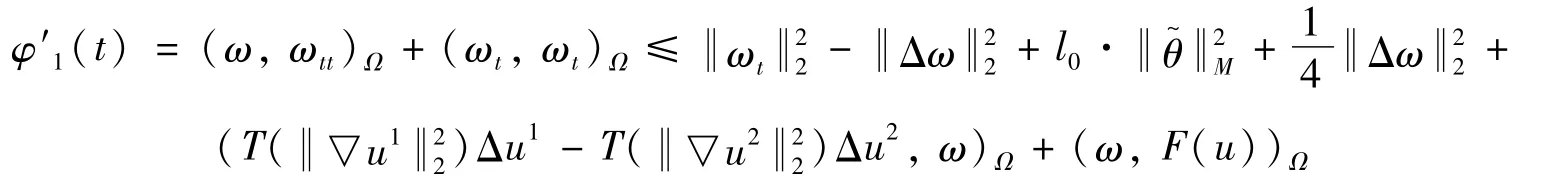
由Hölder不等式以及Poincare不等式有

由Hölder不等式以及拉格朗日中值定理有

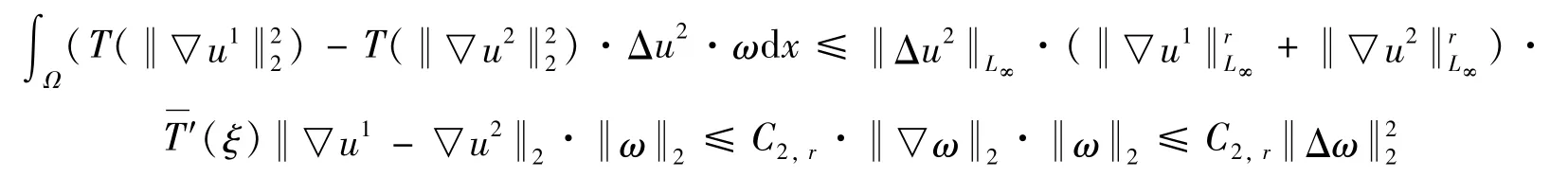
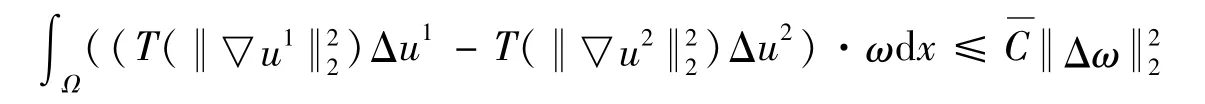
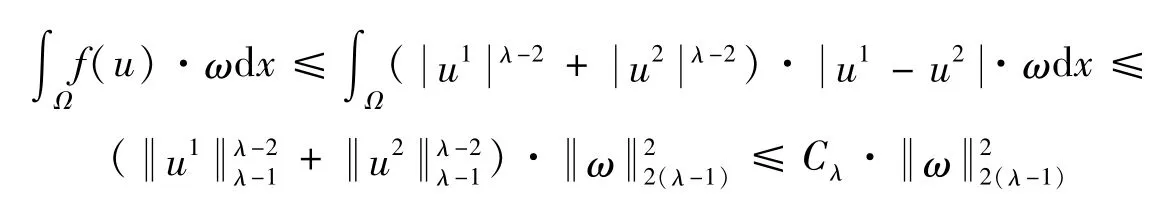
因此有

步骤3令

对φ2（t）求导，由式（36）中的第2个方程有：

其中

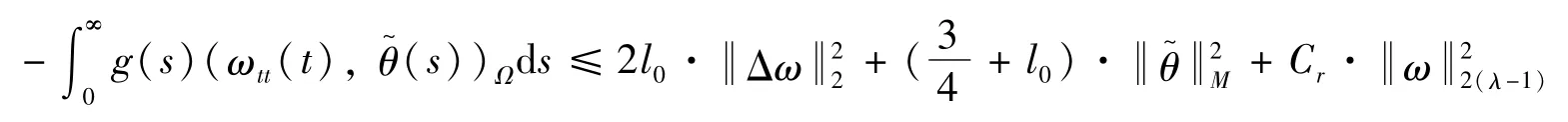
由Young不等式可知：

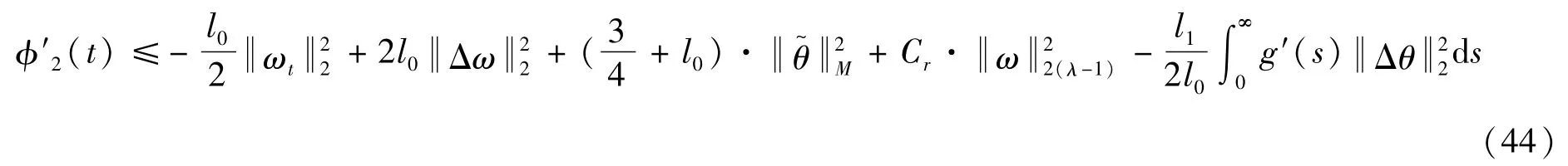
步骤4令J（t）=E（t）+ε1φ1（t）+ε2φ2（t）

其中0＜ε1，ε2＜1，则J（t）是想要的Lyapunov函数。并且存在σ＞0，对于任意t≥0有下面的估计成立：

其中σ1=1-σ，σ2=1+σ。

证明：由Young不等式以及Poincare不等式有：

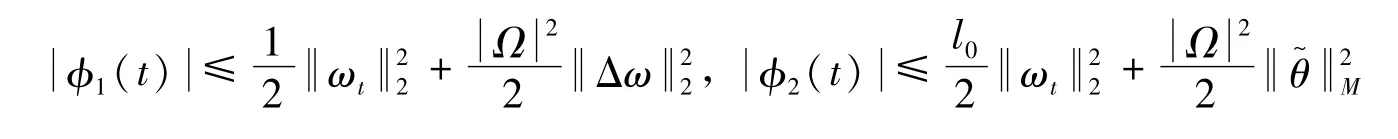
那么存在一个常数σ0＞0，使得

令σ1=1-σ0，σ2=1+σ0，σ1，σ2＞0，便得到不等式（45）。

步骤5 证明有非常小的ε＞0，以及与B相关的正常数cλ＞0，满足

证明：根据步骤4中J（t）的定义知：

根据式（42）～（44）的估计有：

结合式（48），不等式（46）得证。由式（45）以及Gronwall不等式可知：

又因为σ1E（t）≤J（t）≤σ2E（t）可得：

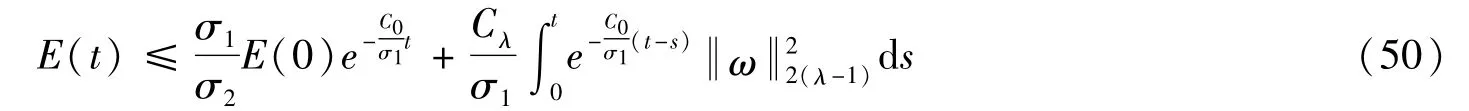
定理2动力系统（E，St）在E上的任何正向不变有界集B都具有拟稳定性。

证明：令X=H2∩H10（Ω），Y=L2（Ω），Z=L2g（R+，H20），则X能够紧嵌入到Y中，根据解对初值的连续依赖性，有

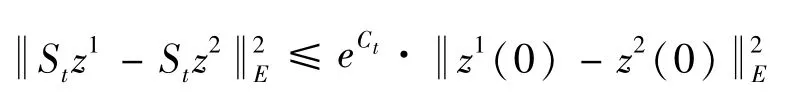
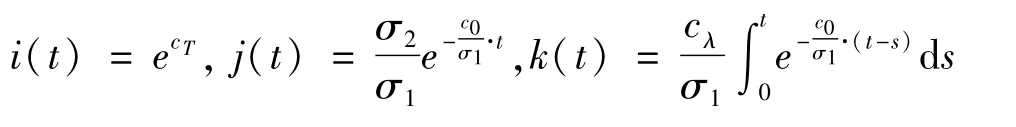
有j（t）∈L1（R+），且成立。又因为B是E上的有界集，所以k（t）在［0，∞）区间内具有局部有界性。由式（35）可知：

由定义4可知：（E，St）在E上任意一个正向不变有界集B中都具有拟稳定性，从而证明了动力系统（E，St）是渐近光滑的动力系统。

定理3（A1）～（A3）成立，动力系统（E，S（t））具有紧的全局吸引子，Mu（N）为N传出的不稳定流形。

证明：由引理7能够证得（E，St）是一个梯度系统，定理2证得（E，St）是渐近光滑的，根据引理8可得Φ（x）在E上任意有界子集上具有有界性，同时ΦR也具有有界性，结合引理9得到动力系统平衡解集N也具有有界性。根据引理3可知动力系统（E，St）存在紧的全局吸引子。

3.3 有限分形维数、正则性及广义指数吸引子

定义5［15］若X是度量空间，E为X上的一紧集。E的分形维数定义如下：

其中n（E，r）是能够覆盖集合E的闭球的最小个数，闭球的直径为2r。

定义6［15］若A是一个具有有限分形维数的正向不变集，并且对于X上每一个有界集K，都存在正常数tK，CK，rK，对于任意t≥tK满足：

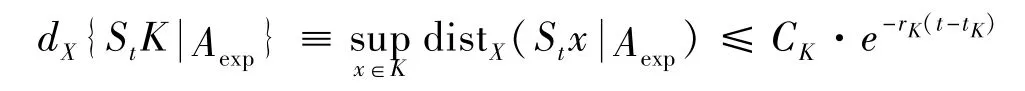
则X上的紧集Aexp是动力系统（E，St）的惯性流形（分形指数吸引子）。

定理4 动力系统（E，St）全局吸引子A的分形维数是有限的。任意属于A的全轨道{u（t），ut（t），θ（t）：t∈R} 存在如下正则性：

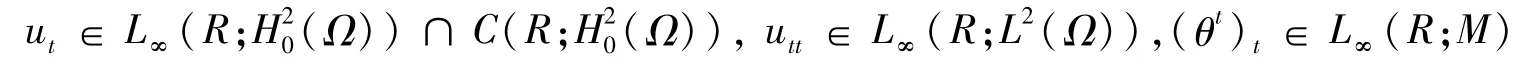
并且对于R＞0，有：

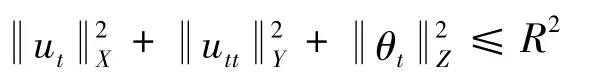
证明：根据家理2、定理3可知，吸引子A的分形维数有限同时能得到全轨道关于时间的正则性。

定义7令A=-Δ是定义在L2（Ω）上的拉普拉斯算子，D（A）=H2（Ω）∩H10（Ω）

刻度空间：

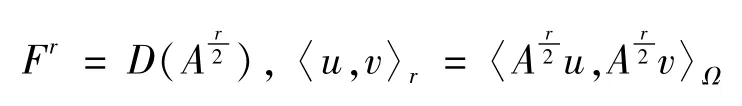
定义空间：

当t≤s时：Fs可以嵌入到Ft中。

定理5若（A1）～（A3）成立，那么动力系统（E，St）在空间E上存在广义指数吸引子。对于任何γ∈（0，1］，空间E上的广义指数吸引子于拓展空间E-γ内分形维数有限。拓展空间定义如下：

证明：令B={ y|Φ（y）≤R}，Φ（·）为引理7所定义的严格的Lyapunov函数。对于足够大的R，集合B为正向有界不变吸收集，这样便可得到（E，St）在B内具有拟稳定性。

下面分2种情况讨论拓展空间中广义指数吸引子的存在性。

1）当γ=1时

B是正向不变有界吸收集，关于初值φ0=（u0，v0，θt0）的一个解φ（t），由式（20）知存在一个CB＞0对于任意T＞0，有：

所以对于任意0≤t1＜t2＜T有：

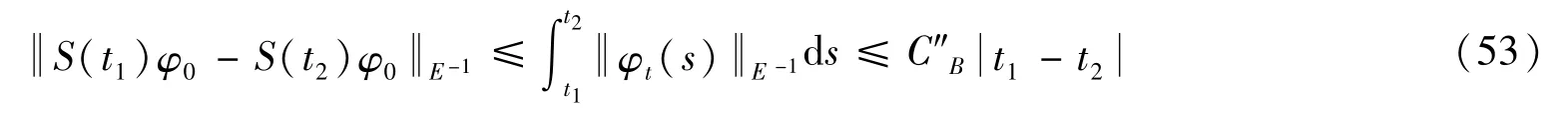
那么t→Sty于E-1中具有Hölder连续性。动力系统（E，St）存在分形维数有限的广义指数吸引子。

2）当0＜γ＜1时

由插值不等式，对于任意的g∈Fm都存在一个正常数Cm＞0，（m=0，1，2），满足

B是半径为r0的球中的一个正向不变有界集，φ（t）=（u（t），ut（t），θt）∈B。因此有：

结合式（55）～（57）有：

因此对于任意的φ∈B，映射t→Sty于扩展空间E-γ内具有Hölder连续性。动力系统（E，St）在E-γ中存在广义指数吸引子同时其分形维数有限。