具有两种滞量的不确定随机时滞系统的稳定性及鲁棒控制*

潘 超，王汝凉，庞健婵

(南宁师范大学 a.数学与统计学院；b.物理与电子工程学院； c.计算机与信息工程学院，广西 南宁 530100)

0 引言

近几年，带有不确定项和时间滞后的系统受到较大关注，国内外有许多专家学者对此进行深入的研究，并取得成果[1，2].文献[3，4]、[5]、[6]都研究中立型随机时滞系统的稳定性，其中，文献[5]对常时滞的不确定中立型随机系统的均方指数稳定性问题进行了研究，给出相应的Lyapunov函数的构造方法，再将积分不等式与LMI相结合，得出系统稳定的条件.文献[1]、[7]、[8]则是对变时滞的不确定随机系统的稳定性问题进行研究，其中文献[1]通过构造L-K泛函，并处理含变时滞的项，结合LMI及Schur补引理得出系统稳定的条件.文献[9]研究了含常时滞的滞后型的随机时滞系统的稳定性，引入一个非线性扰动项，通过不等式的技巧，扩大稳定性的判别范围.文献[10]运用一个新的积分不等式引理来降低计算复杂度，得出含变时滞的不确定随机时滞系统时滞相关稳定的条件.文献[11，12]则是研究了一类具有多个常时滞的中立型随机时滞系统的鲁棒H∞控制问题.文献[13]研究了一类具有三种不同的常时滞的随机时滞系统的均方稳定性，通过选取不同长度的积分区间构造不同的Lyapunov泛函，得出均方稳定的条件，但该方法所构造的函数较复杂，计算量较大.文献[14]研究了一类随机时滞系统时滞无关稳定的条件，通过构造Lyapunov函数，由相关定义得出系统时滞无关稳定的条件.

上述文献只对含常时滞或变时滞的系统进行探究.文献中对同时含常时滞和变时滞的系统进行探究的文献也较少.本文主要研究同时含有常时滞和变时滞的不确定随机系统的随机稳定性问题. 为降低系统的保守性，我们在此系统上增加积分项. 构造新的Lyapunov函数，再用公式It以及积分不等式处理构造的函数，得到一类二次型函数. 根据该函数构建对应的对称矩阵，然后利用Schur补引理，建立这类不确定随机时滞系统随机稳定的充分条件，再运用类似方法对系统的鲁棒H∞控制问题进行研究, 获得系统具有鲁棒H∞性能γ的条件.最后运用文献[4]中的LMI工具箱进行数值计算，验证结论的可行性与有效性.

1 问题描述

考虑不确定随机时滞系统

(1)

该系统中x(t)∈Rn为状态向量，滞量h0(t)是满足

条件的时变连续函数，h、μ为常数；ω(t)是定义在完备的概率空间(Ω,F,P)上的维纳过程，有E[dω(t)]=0，E[dω2(t)]=dt；φ(t)表示定义在区间[-μ,0]上的连续初始向量函数，并且有

A1(t)=A1+ΔA1(t),A2(t)=A2+ΔA2(t),A3(t)=A3+ΔA3(t),A4(t)=A4+ΔA4(t),

其中A1,A2,A3,A4以及E1,E2,E3,E4都表示已知的适当维数的常矩阵，而矩阵ΔA1(t),ΔA2(t),ΔA3(t),ΔA4(t)为适当维数的不确定矩阵，并且这些矩阵满足式子

[ΔA1(t)ΔA2(t)ΔA3(t)ΔA4(t)]=MH(t)[I1I2I3I4].

该式中I1,I2,I3,I4,M为适当维数的常矩阵，而H(t)为具有Lebesgue可测元素的适当维数的未知时变矩阵，且满足

HT(t)H(t)≤E.

式中，E为适当维数的单位矩阵.

对于上述系统，我们研究它的鲁棒H∞控制问题，即考虑以下不确定随机时滞系统：

(2)

其中u(t)∈Rm表示控制输入，z(t)∈Rq表示被控输出，v(t)∈Rp则表示定义在L2[0,∞]上的外部扰动信号，其余符号含义与条件与系统(1)相同.

引理1[12]给定实矩阵U1,U2和U，其中U>0，则对于适当维数的任意向量x,y，有下列不等式成立：

引理2[11]已知A,D,S,W和F是给定的适当维数的实数矩阵，且W>0,FTF≤I，则对任意标量ε>0，向量x,y∈Rn，有

2xTDFSy≤ε-1xTDDTx+εyTSTSy.

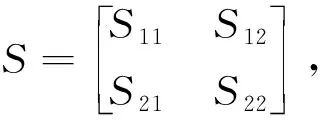
(1)S<0;

引理4[10]给定实数a,b与对称正定矩阵P,P∈Rn，若a>b，x是[0,a-b]到Rn的向量函数，则有如下不等式：

2 主要结果

根据上述条件和引理，对系统进行一定的处理可得出系统的随机渐近稳定和具有鲁棒H∞性能的条件，即以下定理.

定理1给定标量h>0,μ>0和k，如果存在对称正定矩阵P,G,G1,Z,Z1以及标量ε>0，使得以下LMI成立：

其中，

μ2Z2+(E-Z1)-1+(E-Z)-1,

则系统(1)是随机渐近稳定的.

证明构造如下Lyapunov函数：

V=V1+V2+V3,

(3)

其中，

V1=xT(α)Px(α),

(4)

(5)

(6)

对函数V运用It公式可得到

dV=LV+2xT(t)P[E1x(t)+E2x(t-h)+E3x(t-h0(t))+

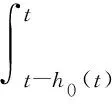
(7)

而在式子中,

LV=LV1+LV2+LV3.

由式子(3)～(7)得

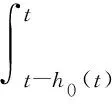
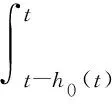
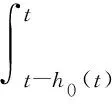
LV2=xT(t)Gx(t)-xT(t-h)Gx(t-h)+xT(t)G1x(t)-

(1-h0(t))xT(t-h0(t))G1x(t-h0(t)),

由引理4可得到

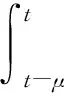
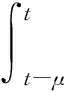
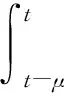
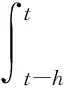
LV2≤xT(t)Gx(t)-xT(t-h)Gx(t-h)+xT(t)G1x(t)-

由引理1和引理2可知

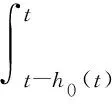
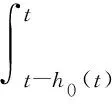
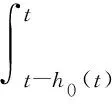
2xT(t)P[ΔA1(t)ΔA2(t)ΔA3(t)ΔA4(t) 0 0]ρ(t)=

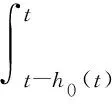
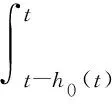
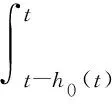
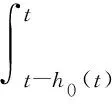
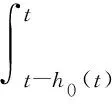
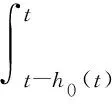
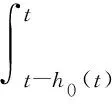
在上式中E为适当维数的单位矩阵，

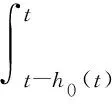
由此可以得出

LV=LV1+LV2+LV3≤ρT(t)Πρ(t),

其中，

其中，

由引理3可得，Π<0等价于Δ<0,所以系统(1)是随机渐近稳定的.

定理2对于给定的标量h>0,μ>0和k，若存在适当维数的正定对称矩阵P,G,G1,Z,Z1以及标量ε2>0，使得线性矩阵不等式

其中，

成立，则不确定随机时滞系统(2)具有鲁棒H∞性能γ.

证明由定理1知不确定时滞系统(1)是随机渐近稳定的，于是可假设

此时类似于定理1证明方法构造Lyapunov函数，则有

在上式中，

g(t)=x(t)+B2v(t),

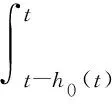
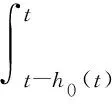
2xT(t)PMH(t)I2dρ1(t)≤2xT(t)P[A1x(t)+A2x(t-h)+A3x(t-h0(t))+

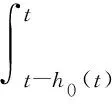
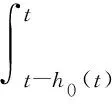
(1-k)xT(t-h0(t))G1x(t-h0(t)),

其中，

综上可得

其中，

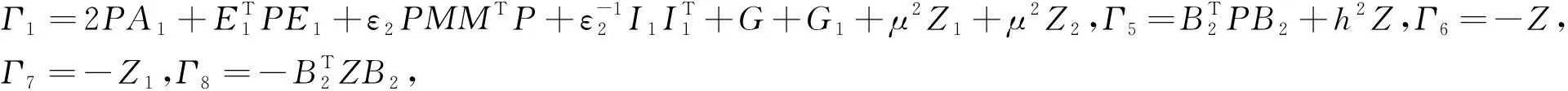
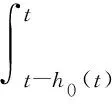
从而

结合假设可知

这里，

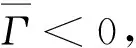
3 数值算例

当n=2时，对于时滞不确定随机系统(1)，令

此时运用MATLAB软件中的LMI工具箱可得

ε=0.00142.

4 结论

本文主要研究同时含常时滞与变时滞的不确定随机时滞系统的随机稳定性的问题，通过构造新的Lyapunov函数，对所构造的Lyapunov函数运用It公式及相关引理进行处理，调整好系统中的常时滞与变时滞的数量关系，再用求线性矩阵不等式可行解的方法来求出使得系统稳定的相关变量，最后通过数值算例验证了本文方法的有效性与可行性.