面向ECDSA的低复杂度多标量乘算法设计
2022-04-26刘志伟赵石磊
黄 海,那 宁,刘志伟,于 斌,赵石磊
(哈尔滨理工大学 计算机科学与技术学院,黑龙江 哈尔滨 150080)
数字签名往往是通过公钥密码来进行的,与物理签名相比,具有不能被他人更改的特性,通过身份认证和密钥协商可以保证通信安全[1]。在数字签名体系中,与同为公钥密码体制的RSA算法相比,椭圆曲线密码(Elliptic Curve Cryptography,ECC)的加密和解密使用的密钥长度较短,可以减少存储空间和功耗,适合在有限的硬件资源上体现[2]。根据椭圆曲线密码应用或密码协议所规定的运算规程,现有的协议常见的有椭圆曲线密码数字签名算法(Elliptic Curve Cryptography Signature Algorithm,ECCSA),椭圆曲线密码密钥交换协议(Elliptic Curve cryptography Diffie-Hellman,ECDH)和加密解密机制。椭圆曲线密码算法性能依赖于标量乘算法运算性能,标量乘又可分解为点加(计算P+G,计算量用A表示)、倍点(计算2P,计算量用D表示)、三倍点(计算3P,计算量用T表示)和五倍点(计算5P,计算量用Q表示)等运算。
在生成公钥时,ECDSA签名过程和ECDH密钥交换过程中使用的是单标量乘算法,在ECDSA验签过程中使用的是多标量乘算法[3]。单标量乘主流算法有倍点——点加二进制方法(Doubling and Addition method,D&A)[4],非邻接表示形(Non-Adjacent-ForM,NAF)[5]和带窗口的非邻接表示形(window width-Non-Adjacent-Form,wNAF)[6]等算法,标量非‘0’概率分别为1/2、1/3和1/(w+1)。这些算法核心思想是通过额外的预处理,来扩大标量k中的0的位数减少点加的次数,来加速标量乘。然而,窗口w扩大不仅使汉明权重下降,也导致预处理的计算复杂度大幅度增长。目前,文献[7]所提出的多基链思想因其独特的运算优势也成为了标量乘讨论的热点之一。根据基的个数,可以分成双基链(Double-Base Chain,DBC)和多基链(Multi-Base Chain,MBC),多基链的宗旨是将标量生成如下形式:
(1)
以多基链为优化方向的算法存在一个构建多基链时间长短的问题。根据贪心法生成的思想,若构建的链过大,则会导致标量乘运行变慢;若构建一个最优的链,则又会导致用在构建的时间上过长。文献[8]优化了三基链并提出了优化的5P运算,重新排序了基底有关{2.3.5}的运算顺序。文献[9]通过设计一个基于伪四维投射坐标的多基链算法来优化构建多基链的方式,从而使得整体开销相对于常规算法降低了8.7%,文献[10]对双基链进行优化后可以保证相对比wNAF优化了超过60%。文献[11]设计了一种基于2,3的双基链保证比NAF优化超过45%。
对于多标量乘算法,主流的算法有Shamir[12],联合稀疏形式(Joint Sparse Form,JSF)[13],联合双基链算法(Joint Double-Base Chain,JDBC)和联合多基链算法(Joint Multi-Base Chain,JMBC )。Shamir和JSF的汉明权重分别为3/4和2/3。JMBC在MBC的基础上,将两个标量联合表示为
(2)
文献[14]提出了一种高效的转换联合三基方式。该方法设计很简单,使用的硬件较少。文献[15]对JSF算法和JMBC进行了分析比对,并在三基链的基础上进一步优化,大大提高了ECDSA的速度。文献[16]对JMBC的算法思想进行了详细的描述和分析。文献[17]指出A、D、T和Q在雅克比坐标下的花费分别为12M+4S,4M+6S,6M+10S和15M+10S,其中M和S分别表示模乘和模平方,模乘和模平方本质上都是模乘,这里可以近似将模乘和模平方视为同一运算(模乘和模平方的计算比例约为0.8M=1S[18])。只需通过统计上述操作的模乘次数即可评估复杂度。ECC的整体运算是在有限域上运行的,其模乘等操作均有取模运算,可以保证数据不会出现数据越界情况。并且,多基链所出现的非0位和0位的概率并不固定,无法通过分析获得私钥值,可以保证其私钥的安全性。由于在ECC系统既要用到单标量乘算法也要用到多标量乘算法,且为了追求效率常常采用不同的多标量乘算法和单标量乘算法分别进行运算处理,这意味着未考虑其他情况下重新进行标量乘算法的调用会导致计算复杂度的提升。
目前关于上述问题的解决方法,文献[19]在KSS曲线下提出了一种倾斜的Frobenius映射技术,并在其基础上设计了一个快速算法。文献[20]设计了一种基于“平行点倍(点加和倍点平行)”的适用于单标量乘算法和多标量乘算法的并行结构,并保证所用的时间和NAF算法几乎相同。文献[21]通过基于窗口的方法进行了加速,使其相对于shamir和NAF优化了至少7.9%。文献[22]使用了GLV方法来进行多标量乘算法的优化,保证在三维或四维GLV方法性能最好。文献[23]利用三维GLV方法探索了在r坐标系上的快速标量乘法。构造并实现了两种三维微分加成链,比使用DJB链的双标量乘法快约6%。文献[24]以2,3,7为基底的多基链整数表示形式及两种多标量乘快速算法,在素数域上,至少比传统算法优化3.1%。文献[25]使用了双基分解方法并进行对Montgomery曲线和Edwards曲线混合来进行加速。
笔者通过整除基底{2,3}并对二者不能整除的部分取模3x2y的方式来构建JDBC表示形式,同时对余数进行预处理来进一步降低计算复杂度,从而保证了在减少预处理的前提下避免了因分别运算处理导致的计算复杂度提升的问题。
1 低计算复杂度多标量乘算法设计
无论在ECDSA的签名过程,ECDH密钥交换和ECC的密钥生成过程使用的private_keyG单标量乘算法,还是在ECDSA验签过程中使用到k1G+k2public_key多标量乘算法(G是椭圆曲线上的一个公共点,private_key是私钥,public_key是对应private_key的公钥),都存在着对k1G进行计算。
因此在构建以{2,3}为基底进行转化JDBC的形式中,对两个标量进行整除基底2和3的操作时,不能整除基底的部分则对两个标量进行同时取模3x2y,并对余数有关G和P+G的多倍点操作进行预处理,使得两个标量可以同时处理标量k2和k1的共同部分。当在调用单标量乘的过程中k2是0的情况下,直接对G的预处理进行相应的计算,从而保证了单标量乘和多标量乘算法的正确性。计算形如mG+nP的多标量转换则如下所示:
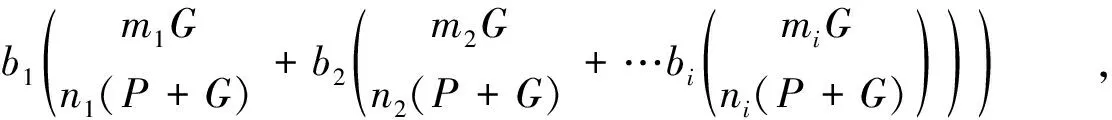
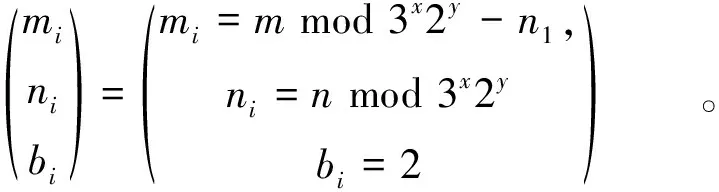
(3)
假设有多标量乘10 536G+17 434P,常见的方法有JDBC、JSF和Shamir。若采用JDBC,转化为
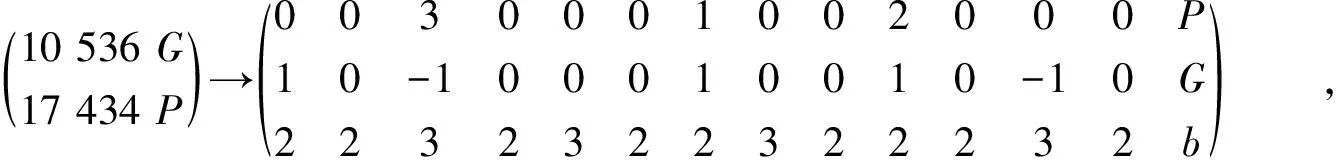
(4)
若采用JSF,转化为
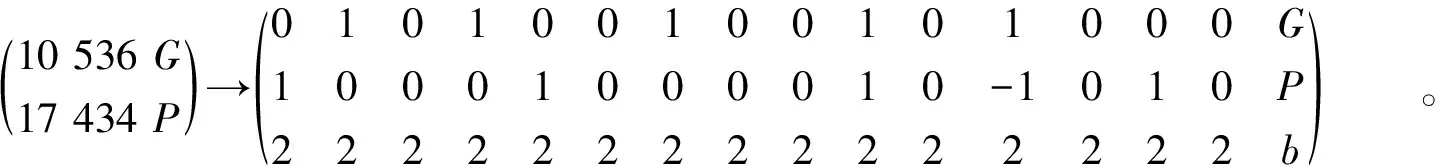
(5)
Shamir形式只是进行二进制展开,这里不进行说明。
使用笔者提出的方法,转换结果如下所示:

(6)
通过式(4)~(6)可以得出,扩大取模操作可以进一步降低计算复杂度,对于10 536G+17 434P,JSF计算15次倍点和10次点加共计调用340次模乘;JDBC进行了8次点加、9次倍点和4次三倍点,共计调用282次模乘;在取模12的时候需要仅进行6次点加,7次倍点和2次三倍点,共计调用198次模乘。
若仅仅是计算private_keyG,假设计算21 057G,常见的方式是wNAF方法,窗口为4的情况下其展开式如下所示:

(7)
单标量乘法以模12为例通过转换后,进行最多对3x2y以下的G的预计算进行查找,就可以得到此次的结果,其转换流程如下所示:

(8)
通过比对可以发现,wNAF需要4次点加,15次倍点,共计调用214次模乘;而式(8)仅需要3次点加、5次倍点和4次三倍点共调用162次模乘。通过式(6)和式(8)可以发现,在验签过程中所使用的多标量乘算法中有关P+G和G预处理部分,在签名、密钥交换的过程中对于G的处理仍然可以使用。
由此可见,根据式(3)推导,该方法理论推导无误且相较于现有方法有一定优化。在此基础上,设计算法如算法1所示,其中步骤①~③是进行预处理操作,步骤④~是进行联合多基链转换,通过预处理的方式进一步地降低了计算量。步骤~是进行标量乘。通过文中的方法,可以保证对于G的预处理既可以在单标量乘中运用,又可以在多标量乘计算中运用。在多标量乘的计算过程中,仅仅需要对P+G重新进行预计算即可,若标量k1和k2相等的时候通过这样的预计算也会进一步降低计算数量。其算法流程图如图1所示。
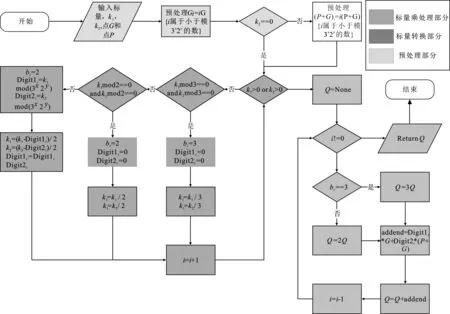
图1 笔者所提出的算法流程图
算法1低计算复杂度多标量乘算法。
输入:标量k1,k2,基点G和点P
输出:标量乘结果Q
① 预处理Gi=iG,i∈{小于3x2y的数}
② 如果k2==0或P=None:
③ 预处理(P+G)i=i(P+G),i∈{小于3x2y的数}
④i赋值为0
⑤k1>0或k2>0时进行循环步骤③~
⑥ 若k1≡0(mod)3且k2≡0(mod)3则执行步骤⑦~⑧
⑦ 将3赋值给bi;0赋值给Digit1i;0赋值给Digit2i
⑧ 将k1/3的结果赋值给k1;将k2/3的结果赋值给k2
⑨ 否则若k1≡0(mod)2且k2≡0(mod)2则执行步骤⑩~
⑩ 将2赋值给bi;0赋值给Digit1i;0赋值给Digit2i
仅剩1艘服役的677型“拉达”级将改装不依赖空气推进动力系统(AIP),但不再进行其他改装。计划建造两艘该级潜艇。
2 低计算复杂度多标量乘算法设计
由于笔者所提出的算法涉及到与单标量乘和多标量乘进行多方面的比较,因此要与多个算法联合进行比较,且MBC表示形式生成后诸如点加、倍点和三倍点的次数难以评估,所以笔者将通过python环境搭建curve-P256模型运行10 000次来取模乘使用次数的平均值用于统计分析,并得到如表1所示的结果。
当x和y值大于3时,其模乘计算次数是大于JDBC和窗口为5的wNAF方法的计算量,因此文中暂不考虑x和y均大于3的情况。通过表1可以发现,当取模12时(即3122),无论单标量乘的计算量还是多标量乘的计算量均是最小。故得到文中最优取模数为12并用于与其他算法比较。
通过模型验证后可以发现,所生成的多基链长度均小于转换前的私钥长度,每一轮有限域运算后都会进行取模限制结果长度,且所调用倍点等操作的分布并不均匀,无法通过分析数据出现规律而分析得到的私钥,从而保证了数据的安全性。
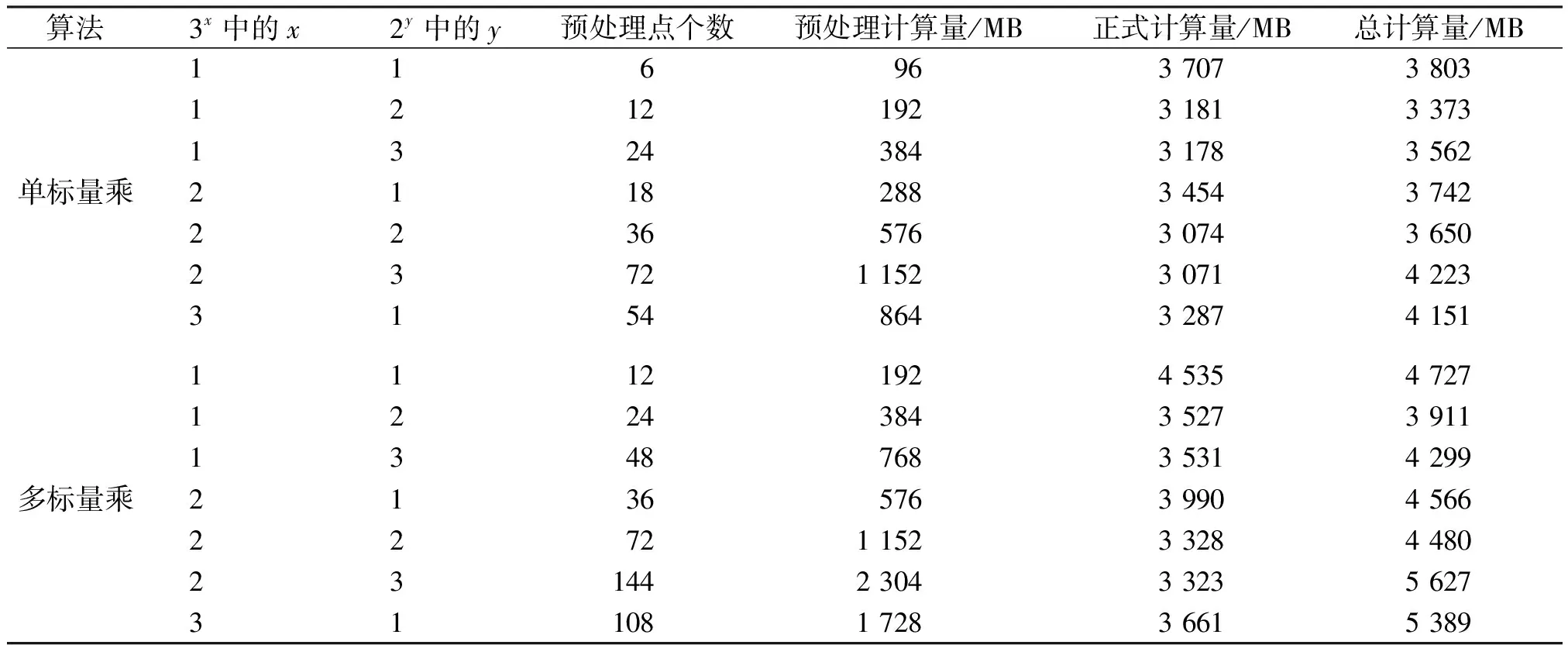
表1 不同取模下文中方法计算复杂度
在比较多标量乘和单标量乘在一组ECDSA中调用时,应通过选取同等汉明权重的算法来进行相应的比较。比如,MBC和JMBC,二者的算法均是无法通过计算得到其平均计算量,需要通过程序的运行来得到平均的运行次数;为了便于统计,这里采用DBC和JDBC进行比较。因此可以保证shamir算法单个标量的汉明权重与D&A不会一致。wNAF算法最优窗口下没有与之对应汉明权重的算法,则采用JSF算法一起运算进行比较。因此,需要对 D&A-shamir,wNAF-JSF,DBC-JDBC进行联合比较,同时对单标量乘和多标量乘各自进行比较才能得到最终的性能分析。D&A、wNAF、Shamir和JSF的正式计算复杂度公式如下所示:
(HA+D)M,
(9)
其中,H代表标量非'0'概率。wNAF算法需要对其最优窗口性能进行分析比较,通过表2可以发现窗口为5是wNAF的最优窗口。

表2 不同窗口wNAF算法计算复杂度
预计算复杂度公式为
(2w-1A+D)M。
(10)
表3描述了各个算法的预处理和正式处理计算复杂度。对于多标量乘而言,虽然笔者所提的方法相较于Shamir算法、JSF算法而言多使用一定预计算,但将整体的计算量优化了至少27.40%。对于JDBC算法而言,采用了相对于JDBC小的预计算,将整体计算量降低了9.84%。仅仅对单标量乘,至少优化了3.88%。
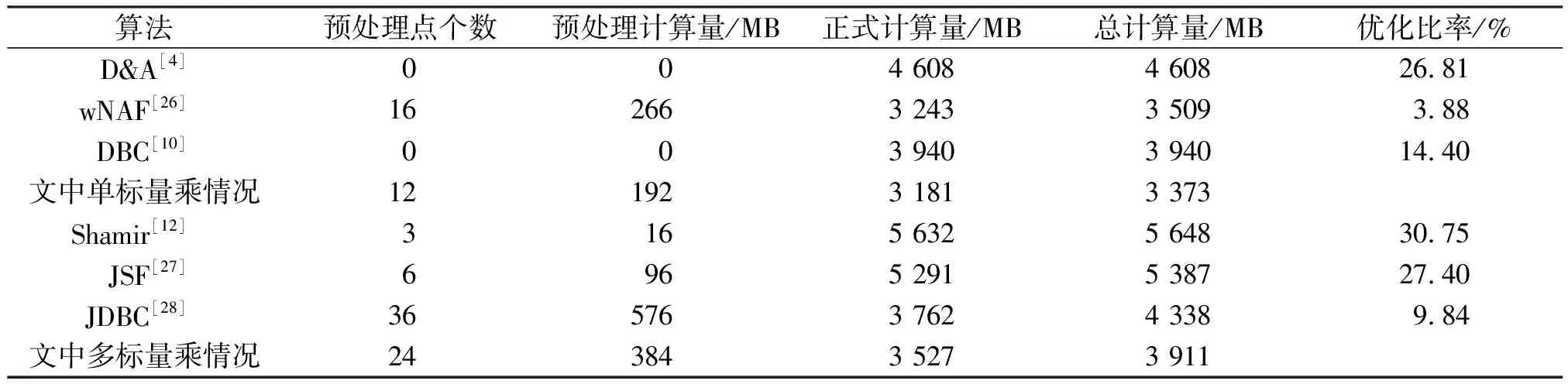
表3 计算复杂度的比较
对于一组ECDSA使用单标量乘和多标量乘算法,表4分别通过标量汉明权重相似的多标量乘算法与单标量乘算法进行比较。
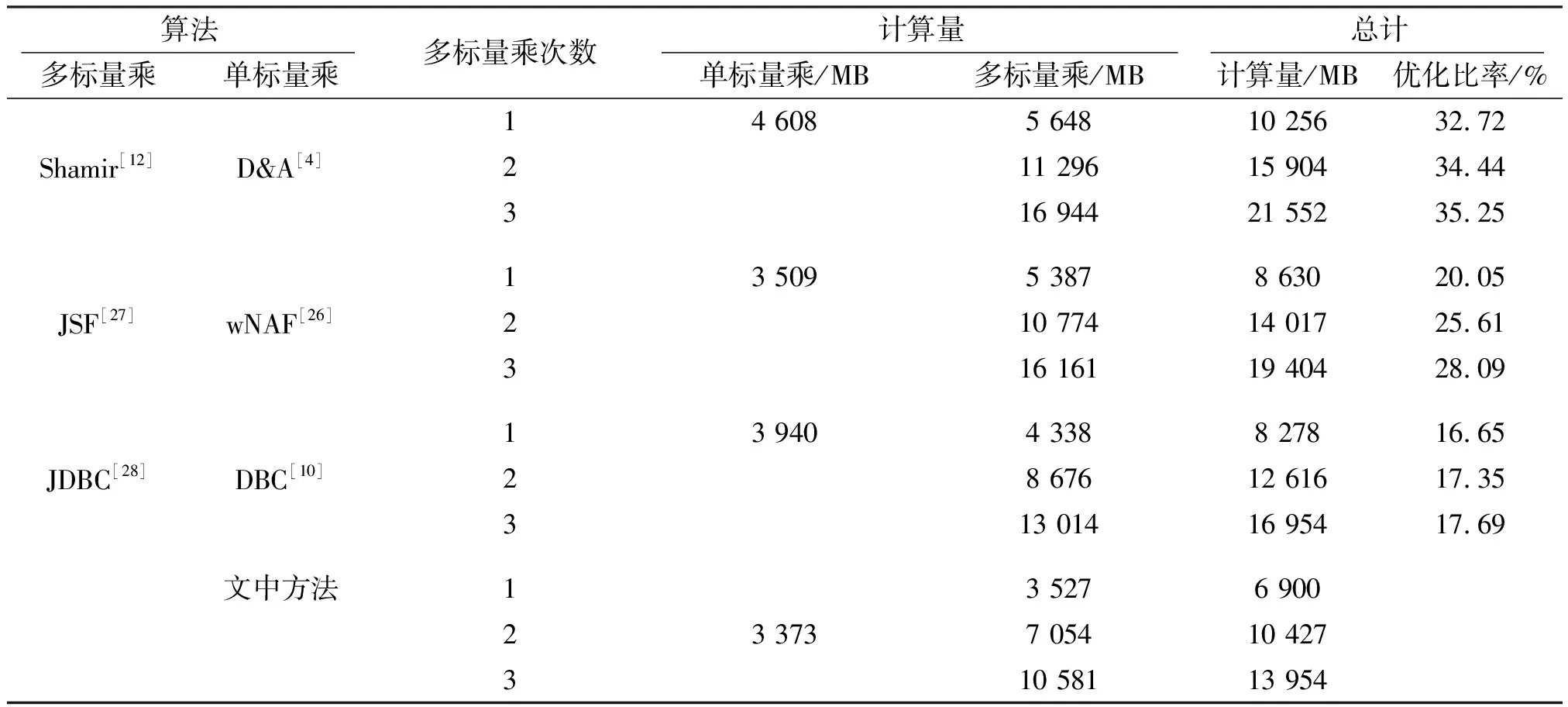
表4 多标量乘与单标量乘的联合计算量比较

图2 10次以内联合多标量乘计算复杂度优化比率
每当单标量乘被重新调用的时候,多标量乘也相当于重新开始计算,因此所讨论的单标量乘每组仅调用1次。通过表4可以发现,在多标量乘运行1~3次的情况下,相较于JDBC-DBC,至少保证优化了16.65%;相较于Shair-D&A算法而言,可以优化32.72%以上;相较于JSF-wNAF算法,可以优化20.05%以上。由于从表4中看出其优化有增加趋势,故图2对文中方法与其余的联合运算10次下的优化比率做了比较,从中可以清晰地看出在10次左右时,文中方法所优化的比率趋于稳定,相对于Shair-D&A、JSF-wNAF和JDBC-DBC优化比率分别趋于36%、32%和18%。保证了一组ECDSA签名验签在运行标量乘方面,相较于现有的算法有着更低的计算复杂度。
为了评估标量乘算法的性能,通过对所设计的算法进行Python建模,使用Python 3.6版本在Core i5-1035G1@1.00 GHz 四核PC上对curveP256曲线进行性能评估。为保证统计结果相对接近,分别采用各算法最优情况时运行10 000次,取其平均运行时间来进行比较。表5就对不同算法的运行速度进行了分析,从表中可以发现,文中所提的方法在单标量乘运算中至少可以提高14.80%的运行速度,在多标量乘的情况下至少可以提升36.91%的速度。
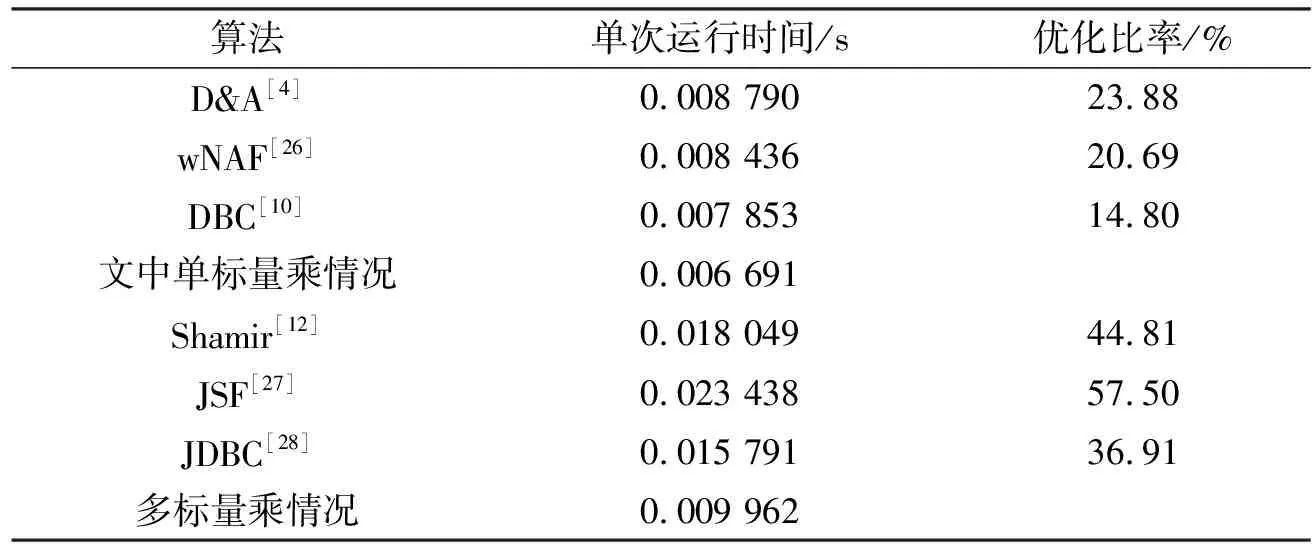
表5 运行速度比较
3 结束语
在对现有的问题进行分析的前提下,笔者提出了一种面向ECDSA的低复杂度多标量乘算法。该算法通过选取模3x2y以下的数进行预处理,在JMBC标量乘思想的基础上,通过适当的扩大预处理来减少标量乘的计算量。在ECDSA的签名或ECDH过程中,在第一次预计算时先对G进行相应的预处理,当遇到ECDSA验签过程时,对P+G进行整体的预计算。在生成标量k1和k2的MBC表示形式时,结合模3x2y运算,并保证在模12时得到最优的结果。计算过程中若存在两个标量之间的差值,则需要通过对G点的点加操作来进行调节。同时该算法在k2为0的情况下也可以计算单标量乘算法。实验结果表明,在curve-P256曲线下相较于其他算法至少降低了约3.88%以上的复杂度,在联合运算的情况下至少可以降低约16.65%以上的复杂度,运行时间减少了约14.80%以上,预计算点相较于wNAF和JDBC算法至少减少了约25.00%。综上所述,笔者所提的方法在计算复杂度计算量以及运算速度上均对以往的方法有一定提高。
