地下圆形粮仓钢板-混凝土组合仓壁弹性应力计算公式推导与验证

揣 君，王录民，何 毅，梁醒培，王振清

1.河南工业大学 土木工程学院，河南 郑州 450001

2.国家粮食和物资储备局，北京 100038

地下粮仓具有低温储粮、绿色生态、节能减损等显著优势[1]，符合我国粮食行业的绿色发展方向，具有广阔的应用前景。组合结构是现代工程结构中一种重要的新型结构体系，其中钢与混凝土组合最为常见，它能充分发挥钢与混凝土两种材料各自的优势，在国内外的应用也越来越广泛[2]。目前，组合结构在大跨度桥梁和高层、超高层建筑中的应用取得了良好的经济、社会效益。相关学者开展了钢板-混凝土组合结构应用在地下粮仓的研究[3-7]，仓壁采用了钢板-混凝土组合结构(以下简称组合仓壁)，它是材料为钢板和混凝土两种性质不同的双层异材圆筒(壁厚与曲率半径之比不大于1/50，属薄柱壳)。组合仓壁在外侧土体围压作用下，空仓为不利工况，需要对其进行强度计算，以满足结构安全性的要求。然而，经典的弹性力学理论仅提供了单层圆筒(均匀介质理想弹性体)受均布压力的应力计算公式[8-9]；该公式对于组合仓壁受外压的双层异材圆筒，显然并不适用。因此，受外压双层异材圆筒的应力计算问题亟待解决。蒋劲松[10]采用Fourier积分的方法建立了夹有泡沫塑料板的混凝土复合井壁应力与位移解析公式，中间泡沫塑料板作为接触条件，井壁为可以滑动的多层复合井壁。姚直书等[11]研究提出了一种双层钢板-混凝土复合井壁设计计算方法，认为由于内、外钢板的约束，中间混凝土层处于3个方向受压应力状态，采用弹性力学3层组合筒法得到混凝土内边缘的主应力。夹有泡沫塑料板的混凝土复合井壁与双层钢板混凝土复合井壁均为3层厚壁圆筒。付春梅等[12]建立了内钢板-混凝土复合井壁计算的力学模型，假设内钢板完全进入塑性状态且混凝土内边缘开始破坏时井壁达到正常使用极限状态。以此进行该复合井壁正常使用极限状态应力计算，先计算出钢板完全进入塑性状态时能够承受的最大径向荷载，将其作为混凝土层的内压力，与外部土压力共同作用，按弹性理论计算混凝土层的应力。该方法引入的假设不一定符合工程实际，应先计算出钢板层和混凝土层各自的应力分布，并以此判定二者的受力状态更为合理。张国鑫[13]提出了钢板-混凝土复合井壁在不均匀侧压力作用下的应力计算方法，将复合井壁作为弹性力学平面问题，采用应力函数法推导了应力计算公式。蔡海兵等[14]采用有限元数值模拟方法对不均匀压力下双层钢板-混凝土井壁进行了力学特性分析。藏德胜等[15]采用ANSYS有限元软件对圆形钢板混凝土井壁受力性能进行了模拟分析。Sun[16]对钢板-混凝土复合井壁进行了试验研究，分析了复合井壁的受力状态，给出了双钢板-混凝土复合仓壁极限荷载计算公式。张厚美等[17]对盾构压力隧洞双层衬砌的力学模型进行了研究，根据不同工况提出了双层衬砌的多种计算模型。Jiang等[18]采用理想弹塑性Mohr-Coulomb 强度准则对压力隧洞进行弹塑性分析。Yu[19]采用统一强度理论对压力隧洞进行弹塑性分析。地下圆形粮仓钢板-混凝土组合仓壁弹性应力的求解问题，是其结构设计计算面临的首要任务之一。因此，作者基于弹性力学推导了受均匀外压双层异材圆筒的应力计算公式，为地下粮仓组合仓壁的设计及应力计算提供理论依据，具有一定的应用价值。

1 计算模型简化

为了研究新型组合仓壁的应力计算问题，建立其简化的力学计算模型如图1所示。空仓工况，组合仓壁外侧承受周围水土侧压力为主，沿组合仓壁高度H的侧压力分布并不均匀；由柱壳理论可知，组合仓壁主要内力是环向轴力，沿仓壁高度Z方向取任意一段作为研究对象，当其高度Δh不大时，可近似认为作用在组合仓壁上的外压是均匀分布的。因此，新型组合仓壁的应力计算问题可归结为受均匀外压双层异材圆筒的应力计算问题。引入假设：组合仓壁的钢板与混凝土通过栓钉连接，假设二者可以共同受力并变形协调；假设装配式地下粮仓的仓顶、仓底板对组合仓壁受力的影响符合圣维南原理。

定义圆筒由内、外两层不同的材料组成，内、外层材料的弹性模量和泊松比分别为E、μ和E′、μ′。如图1b所示，内层筒内半径为R1，内层筒外半径为R2，外层筒外半径为R3，则内层筒厚度为R2-R1，外层筒厚度为R3-R2。外壁承受均布压力q。

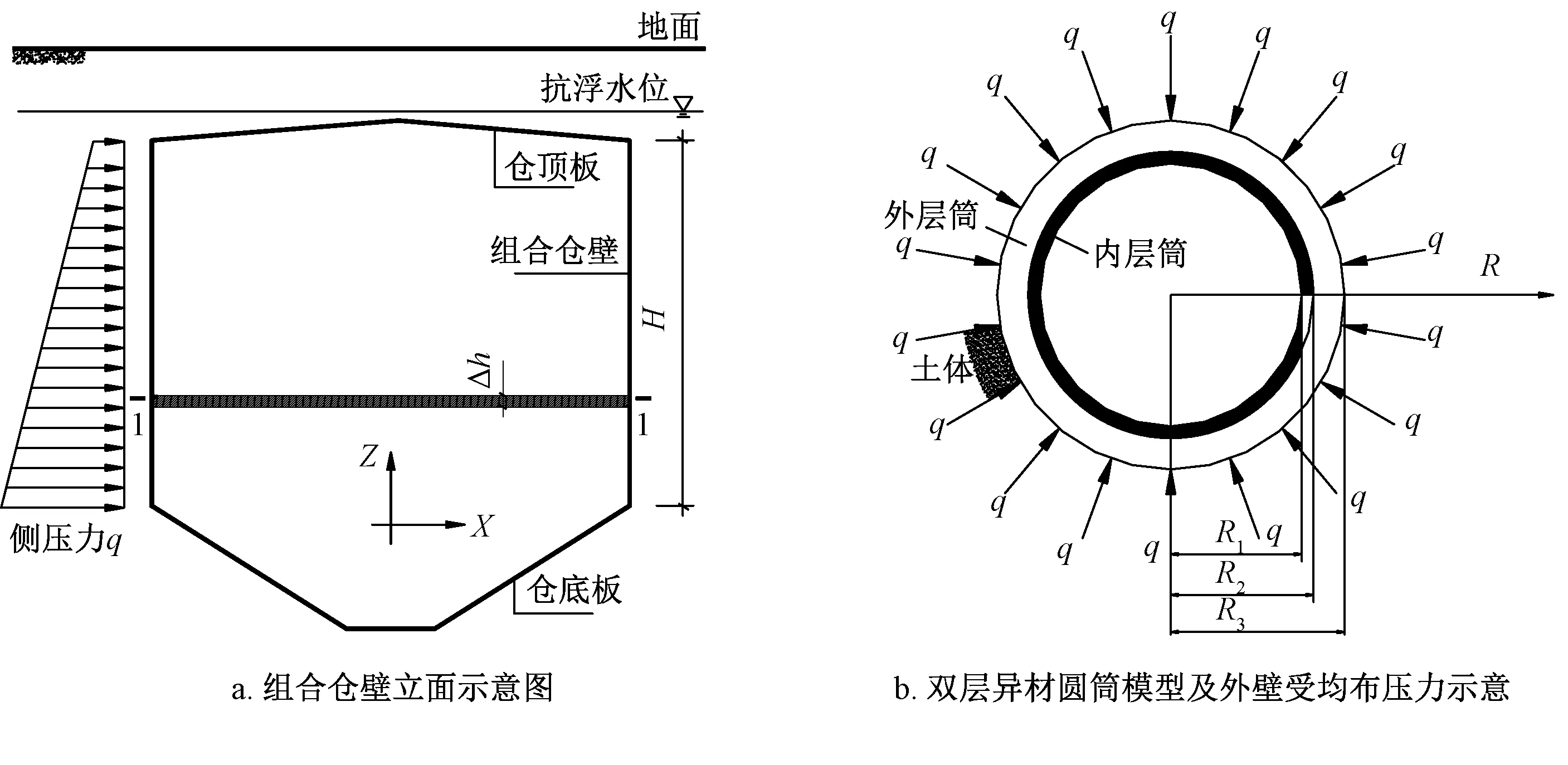
图1 组合仓壁简化计算模型示意图

2 双层异材圆筒应力计算公式的推导

2.1 受外压双层异材圆筒应力求解

由弹性力学可知，圆筒的受力属轴对称问题，假设圆筒为无限长，则可简化为平面应变问题，其应力和位移可以分别引用轴对称应力和相应的位移。

假设内层圆筒的应力：

(1)

假设外层圆筒的应力：

(2)

式中：σr、σφ分别为径向应力和环向应力；r为圆筒内部任何一点到圆心的距离；A、C、A′、C′是4个待求常数，可由以下4个边界条件确定。

(1)应力边界条件

在圆筒的内表面r=R1处：(σr)r=R1=0,即

(3)

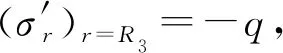
(4)

(2)界面条件

(5)

(3)位移单值条件

由于圆筒是多连体，可以写出两者的径向位移的表达式，其中I、K、I′、K′、θ为任意常数。

内层圆筒径向位移：

(6)

外层圆筒径向位移：

(7)

将式(6)、式(7)简化后得：

(8a)

I′cosθ+K′sinθ。

(8b)

(9)

(4)常数求解

简化归纳后，得到确定4个常数的4个方程。

由式(3)、式(5)、式(9)、式(4)可得，

(10)

(11)

(12)

(13)

将方程(10)—(13)采用矩阵表示为以A、C、A′、C′为未知量的代数方程组。

(14)

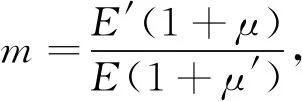
(15)

求解方程(15)可得系数A、C、A′、C′的表达式。为简化系数A、C、A′、C′的表达式，令

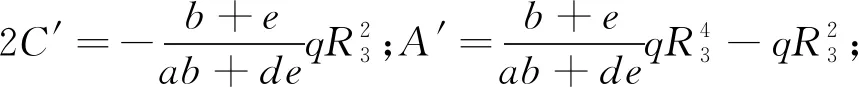
2.2 应力计算公式

将求解得到的系数A、C、A′、C′代入式(1)和式(2)即可得到内外筒体为异种材料、接触面按接触处理的线弹性应力计算解析式。

内层圆筒的径向应力：

(16a)

内层圆筒的环向应力：

(16b)

外层圆筒的径向应力：

(17a)

外层圆筒的环向应力：

(17b)

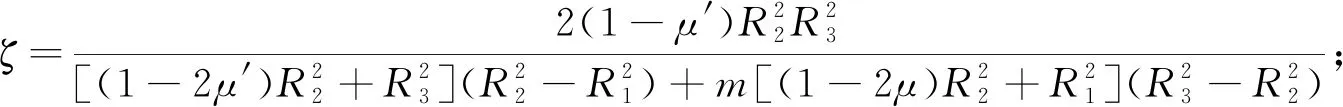
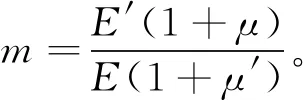
3 双层异材圆筒应力计算公式的验证分析

为验证推导的应力计算公式(16)和(17)的正确性，分别对同种材料和异种材料组成的双层圆筒，采用弹性力学公式解析解和有限元模拟数值解与之对比分析验证。

3.1 同材双层圆筒应力结果对比

对于图1所示的双层圆筒受均匀外压问题，假定双层圆筒的材料为同种材料，即为单层圆筒，故可按弹性力学已有计算公式[20]得到该问题的应力解析解。此外，也可仍然视为双层异材圆筒(两层为同一种材料)，按双层异材圆筒应力公式(16)和(17)进行计算得到该问题的应力解析解。

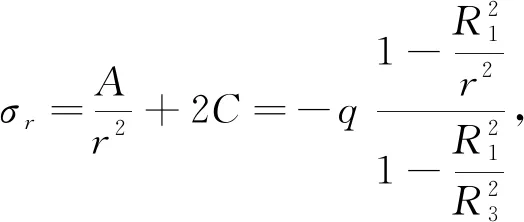
由以上应力表达式可知，同种材料时双层异材圆筒应力公式(16)和(17)与拉梅解答形式相同，验证了推导的应力计算公式的正确性。

3.2 异材双层圆筒应力结果对比

以图1所示的受均匀外压双层圆筒问题为例，假定双层圆筒的材料为异种材料，则弹性力学中受外压单层圆筒应力计算公式不适用。为了对比分析应力，采用ANSYS建模，结果如图2所示，有限元法模拟得到受外压双层异材圆筒应力的数值解；将其与公式(16)和(17)计算得到的解析解对比分析，以进一步验证推导双层异材圆筒应力计算公式的正确性。

工程算例：R1=10.0 m,R2=10.3 m,R3=10.4 m,q=-100 N/m2；E=3.0×1010N/m2，E′=2.0×1011N/m2，μ=μ′=0.3。

按照工程算例的基本参数，先求得双层异材圆筒应力公式(16)和(17)的系数值，即有A=169 700，C=-848.5，A′=14 310，C′=-116.2；得到工程算例双层异材圆筒沿壁厚截面上的径向应力和环向应力解析解，解析解和数值解见表1。

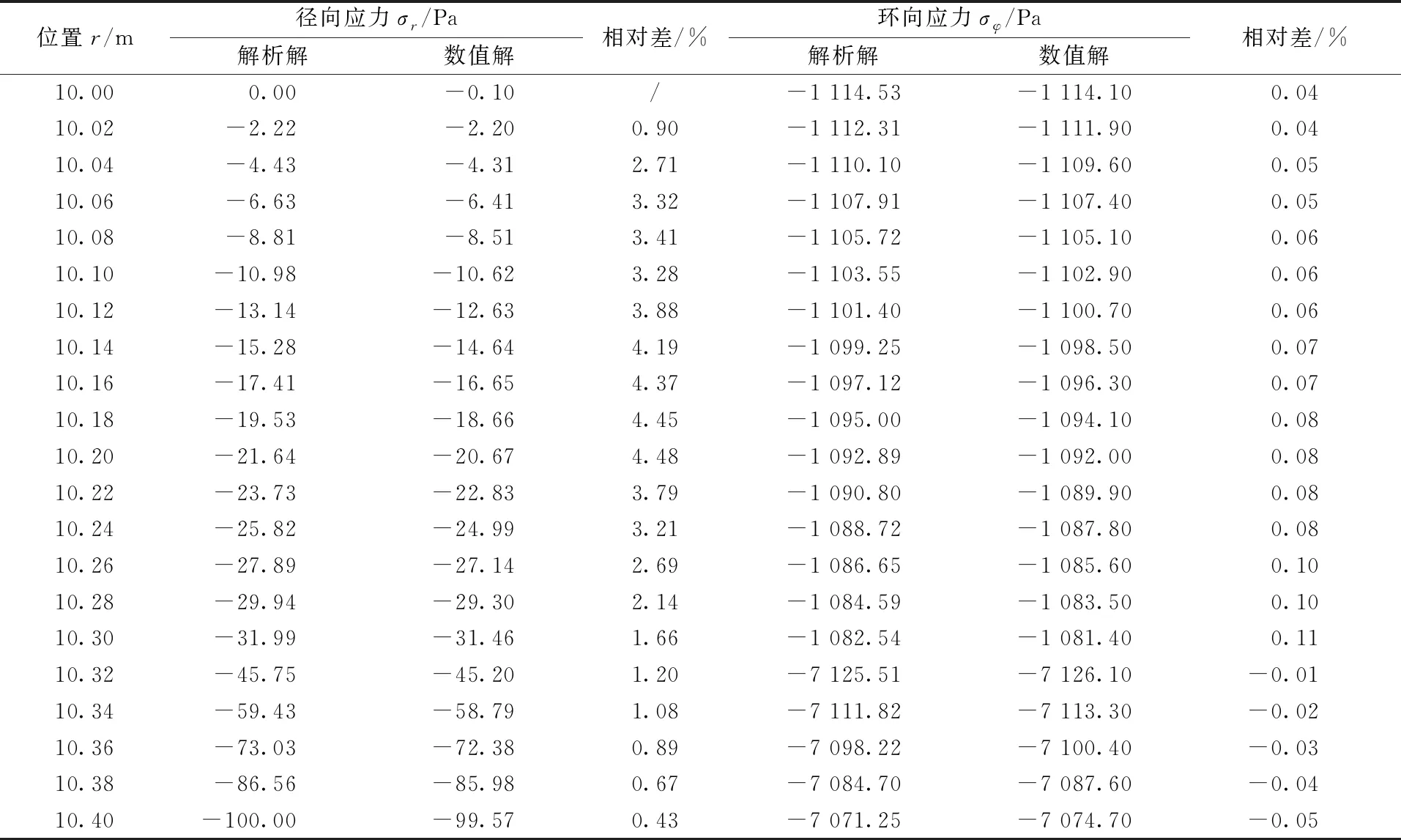
表1 径向应力和环向应力的解析解与数值解

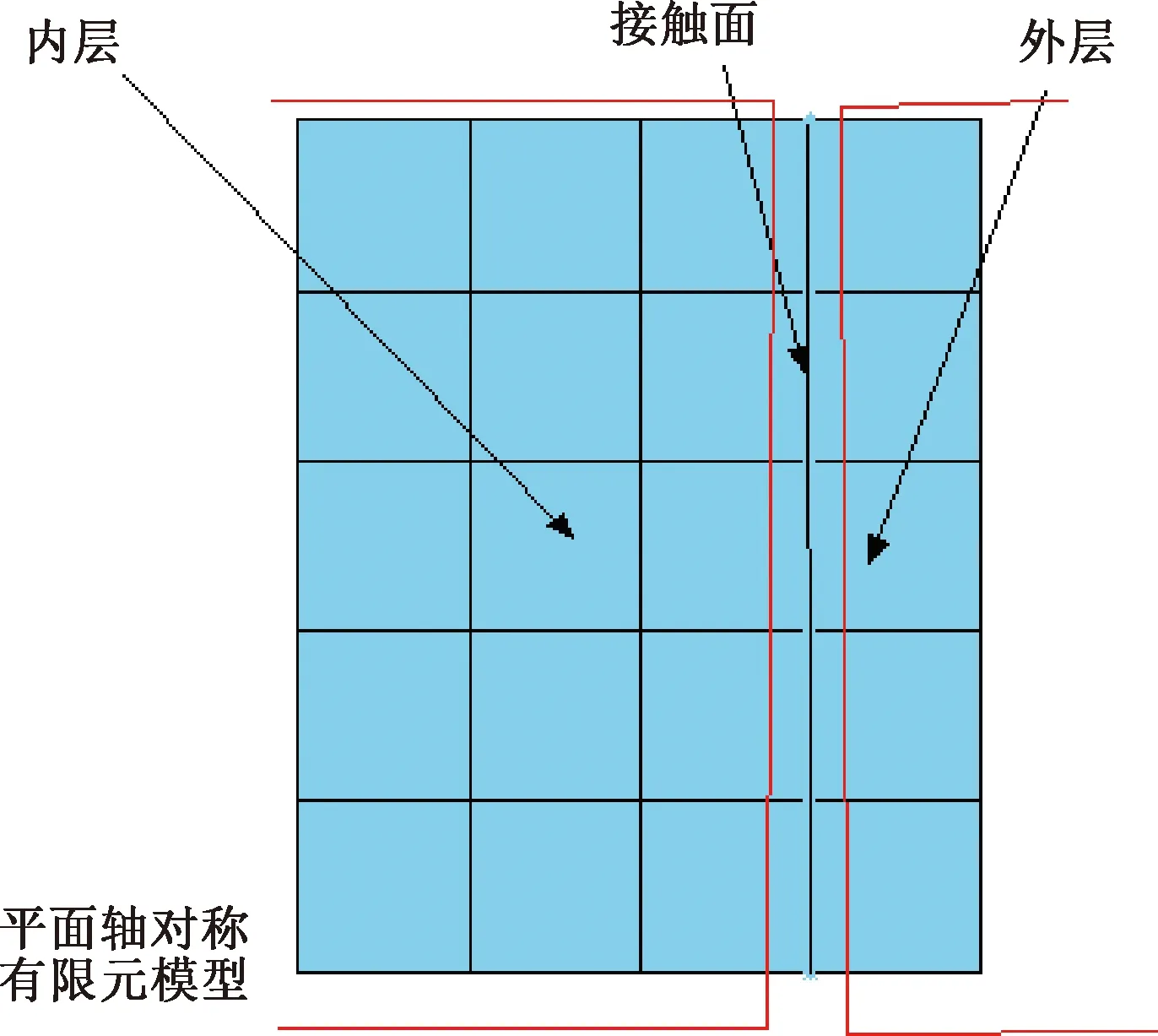
图2 异种材料双层圆筒平面轴对称有限元模型

从表1可知，径向应力最大相对差为4.48%，环向应力最大相对差为0.11%，相对差都在5%以内，特别是环向应力相对差较小，总体上吻合良好，验证了推导的受外压双层异材圆筒应力计算公式适用于钢板-混凝土组合仓壁的应力计算。

4 结论

综上所述，推导的受均匀外压双层异材圆筒弹性应力计算公式解决了地下圆形粮仓钢板-混凝土组合仓壁的应力求解问题，为类似组合结构的强度计算提供了参考。对于建立的受外压双层异材圆筒应力计算公式，分别采用弹性力学中受外压单层圆筒(同种材料)应力计算理论公式和有限元数值分析方法进行了验证分析，结果表明推导的受均匀外压双层异材圆筒应力计算公式是正确的。基于弹性力学理论推导建立的受均匀外压双层异材圆筒应力计算公式，适用于地下圆形粮仓钢板-混凝土组合仓壁的强度计算。