基于L2正则化LSTM的非线性动态系统辨识

徐宝昌 吕 爽 董秀娟 王 健

（1.中国石油大学（北京）信息科学与工程学院；2.中石油北京天然气管道有限公司）

实现良好的控制是提高工业生产过程经济效益、保障生产安全的关键，而实现良好控制的基础就是建立准确的模型。 但现有的化工过程辨识方法大多过于依赖实验获得的数据，这严重地限制了其使用范围。 随着计算机计算能力的提升，DCS在实际生产中逐渐普及，大量的生产数据被存储在本地或云端，这些数据中蕴含着生产过程的各种动静态信息， 如果能充分挖掘DCS中数据的信息，通过一定的模型结构和参数来表达非线性的动态过程，建立良好的替代模型，将能够更好地掌握过程的内在特性，便于研究出更加高效稳定的控制方法， 实现对整个流程的故障预测、控制、监督以及经济效益优化等。

为解决上述问题， 笔者引入深度学习算法中的模型——长短期记忆（Long Short-Term Memory，LSTM）［1］。 LSTM 在 循 环 神 经 网 络（Recurrent Neural Network，RNN） 的基础上引入长短期记忆结构，既考虑了过往信息的影响，也有效地解决了梯度消失或爆炸问题，在手写识别［2］、图像分析［3］及时间序列预测等方面表现出良好的效果。 Yadav A等利用LSTM对印度股票市场进行预测，通过有无状态模型和隐藏层数量对网络进行优化，结果表明LSTM在股票预测上具有可行性［4］；Gonzalez J和Yu W则利用LSTM与神经网络的结合，证明了改进后的方法对于只使用测试输入、不利用以往测试输出的模型而言具有更好的效果［5］；Joohyun W等利用LSTM进行无人水面车辆（SUV）模型的建立，该方法相比传统的线性动态模型降低了浪涌预测误差、偏航率预测误差等，表现出良好的性能［6］。 针对基本结构对数据契合不高的问题，学者们对其结构进行了改变或采用与其他模型、方法相结合的思路，如韩恒贵利用LSTM的变体GRU和混合模型进行绝缘双极性晶体管的故障预测，实验结果表明新方法进行故障预测的均方根值为0.075 6，预测效果有了很大的提升［7］；Yu R等提出一种基于序列相关特征的LSTM-EFG模型用于风力发电预测，该方法对遗忘门功能进行了增强，提高了预测的效果［8］。

在实际应用中，LSTM基础网络由于结构和输入数据不足等问题， 往往会出现模型过拟合、泛化能力低等问题，为此笔者结合常用于解决过拟合现象的正则化［9，10］方法提出基于L2正则化LSTM辨识策略， 并利用非自衡系统TE过程（Tennessee Eastman Process）进行方法有效性的验证。 通过实验表明，该方法具有更快的收敛速度，模型泛化能力更强，对所需辨识数据要求更低，辨识得到的模型可以很好地反映系统的阶跃响应过程，预测系统的输出。

1 L2正则化LSTM模型

1.1 LSTM模型

LSTM 是由RNN 发展而来的重要结构，由Hochreiter S和Schmidhuber J于1997年提出［1］，它在RNN的基础上增加了输入门、输出门、遗忘门和记忆单元4个门限， 能够对长距离依赖问题进行处理，避免梯度消失或爆炸的问题。 LSTM内部结构如图1所示。

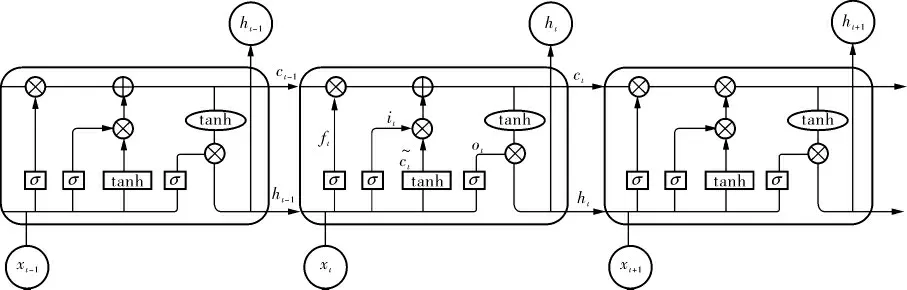
图1 LSTM内部结构

在LSTM的结构中，以t时刻的输入xt和前一时刻的状态信息ht-1作为输入信息，通过内部细胞进行状态单元的填充或移除完成信息更新。 原始的LSTM结构的门限由sigmoid函数与矩阵点乘组成，由于sigmoid函数的输出为0～1之间的数字，因此可以描述信息的通过程度， 其中0代表移除，1代表全部信息通过。 LSTM网络的前向传播可以表示为：

1.2 基于L2正则化LSTM模型

为增强辨识模型的泛化能力，笔者采用可以对参数进行稀疏化的L2正则化方法对LSTM基础模型进行优化，即在原损失函数上加上L2范数正则化项，得到的损失函数J公式如下：

其中，λ为正则化系数，用于权衡正则项与原始函数的比重；n为训练集样本大小；J0为原始的损失函数；ω为权重；yi为模型实际输出；为模型预测输出。

根据上述公式，权重ω的更新为：

其中，η为学习率。

根据式 （7）、（8）， 可以得到基于L2正则化LSTM辨识策略的权值更新公式：

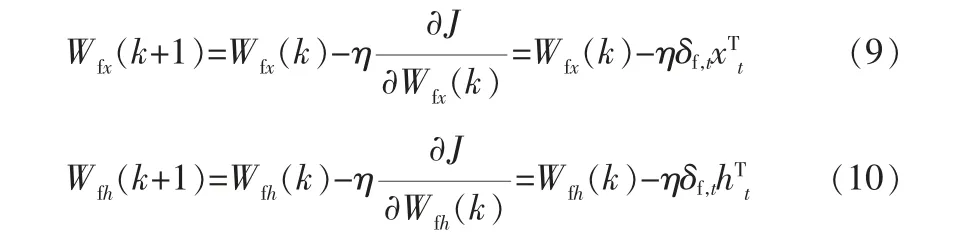
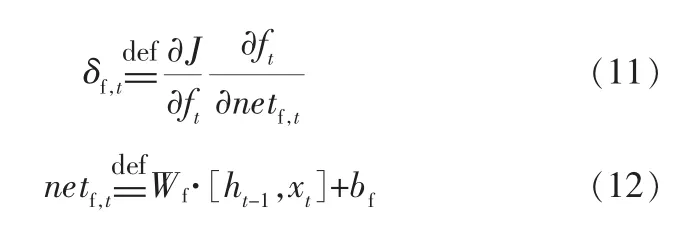
其中，Wfx、Wfh分别为遗忘门更新时输入信息和上一层状态所对应的更新权重；k为时刻；δf，t为损失函数J对于Wf·［ht-1，xt］+bf的偏导数。

其余权值更新公式同理。

2 实验及结果分析

2.1 数据来源及预处理

笔者采用非自衡系统TE过程作为辨识对象。TE过程是一个实际化工过程的仿真模拟，它是由美国Tennessee Eastman化学公司过程控制小组的Downs J J和Vogel E F提出的［11］，被广泛地应用于过程控制技术的研究［12］。整个TE过程可以被用来进行各种各样的过程研究，主要包括装置的控制策略设计、多变量控制、过程优化及预测控制等。

TE过程包含12个操纵变量和41个测量变量，所给出的已知数据集中包含21个预先设定好的故障，其中16个为已知故障（包含阶跃、随机变量等），5个为未知故障。 每一种故障对应两组数据，分别为具有498个数据的训练集和948个数据的测试集。 文中笔者选取12个操纵变量作为输入，产品分离器温度XMEAS11的测量值作为输出，具体的训练集、测试集、验证集来源见表1。

表1 实验中涉及的几组数据集组合

TE过程所提供的数据集来自仿真实验，需要进行时序处理才能符合L2正则化LSTM网络的输入形式。 同时，为消除不同量纲和数量级带来的影响，需将数据集进行0～1标准化处理。 笔者选用以下几种模型评价指标来对辨识效果进行评估，包括ACC （精确度）、MAPE （平均相对百分比误差）、RMSE（均方根误差）及R2（拟合优度）等。 其中，MAPE和RMSE的值越小， 说明模型建立的效果越好；R2衡量的是回归方程整体的拟合度，R2的值越接近1，说明模型的拟合效果越好。 具体评价指标如下：

其中，y-为实际输出的平均值。

2.2 LSTM网络结构设定

文中用前n步时间状态的11个操纵变量数据预测后m步产品分离器温度XMEAS11，即网络输入X={X1（t），X2（t），…，X11（t），…，X1（t-n），X2（tn），…，X11（t-n）}，输出Y={Y（t），…，Y（t+m）}。

利用L2正则化LSTM辨识策略和表1中的第4组数据集进行TE过程辨识，根据网格搜索法确定标准LSTM辨识时的最优参数组合为：隐藏层参数为25，学习率η为0.3，时间步长time_step为2，迭代次数为1 000次。 从［0，10］中选取正则化系数λ的值，观察训练集、测试集和验证集的评价指标变化，其中验证集变化曲线如图2所示。

图2 验证集偏差随正则化系数λ的变化曲线

根据仿真结果可以得到：验证集偏差随正则化系数λ的增加先减小后增大，当正则化系数λ=2时，验证集偏差最小，正则化方法使用前后的评价指标见表2。

表2 正则化方法使用前后评价指标的对比

2.3 实验对比分析

现利用支持向量回归（SVR）、BP和基于L2正则化LSTM的网络（L2-G-LSTM）对TE过程进行辨识与比较，得到的训练结果如图3、4所示，评价指见标表3～6。 所采用的数据集为表1中的4组数据集。

图3 测试集各个样本预测误差百分比

图4 基于第2组数据集各算法的预测结果

表3 基于第1组数据集的评价指标

（续表3）

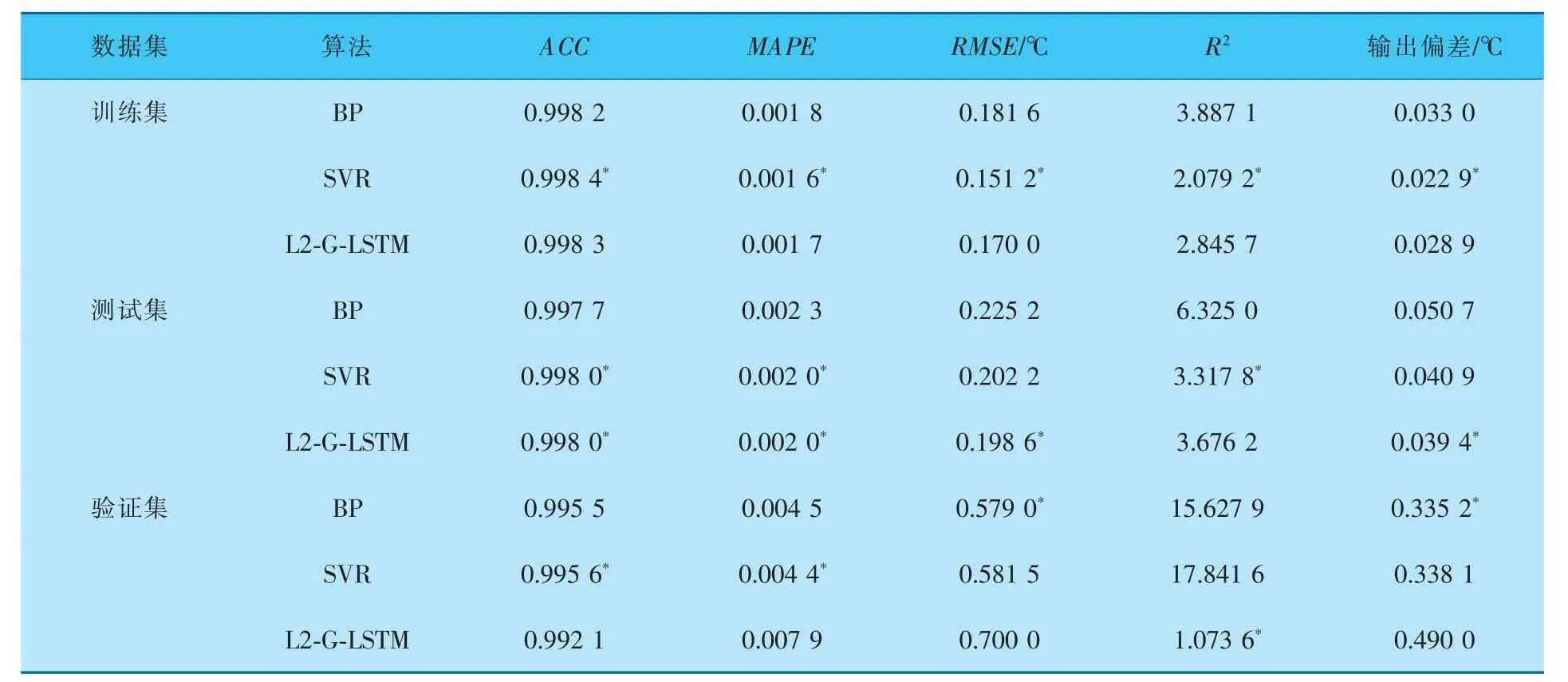
表4 基于第2组数据集的评价指标

表5 基于第3组数据集的评价指标

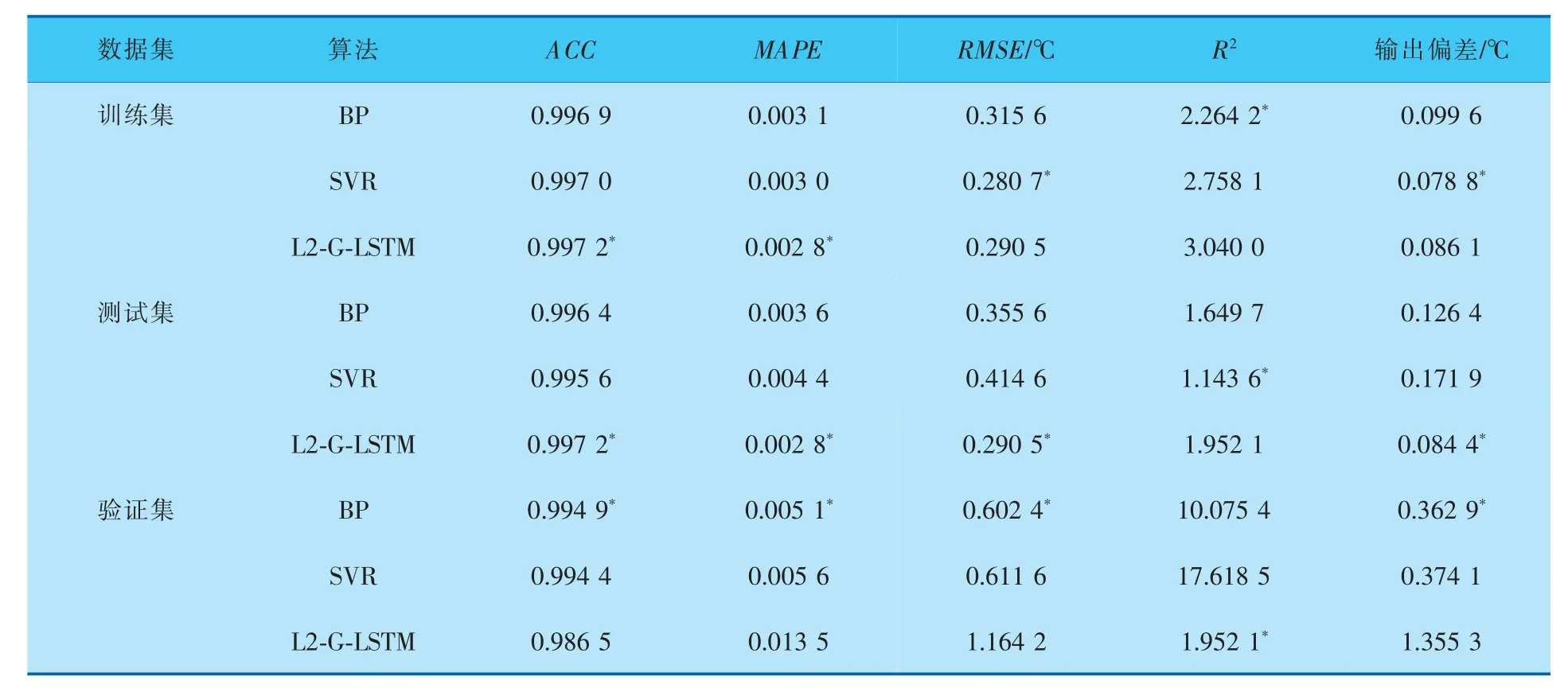
表6 基于第4组数据集的评价指标

从表3～6的结果可以看出， 相较于BP和SVR而言，L2-G-LSTM对TE过程进行辨识时，在训练集和测试集上得到的RMSE、MAPE相对较小，R2和ACC更接近于1，得到的拟合模型更加接近真实模型。 同时根据预测结果和实际输出的对比，L2-GLSTM在验证集上进行验证时，能够更好地反映出系统阶跃响应的各项指标，综合评价指标和预测结果对比结果， 可以充分说明L2-G-LSTM具有更高的泛化能力和更高的辨识精度，能够更好地对非线性动态系统进行建模。 实验中的4组数据集分别对应4种情况，无论在哪种情况下L2-G-LSTM网络基本都能得到综合评价下的最优结果，基于这一点说明基于L2正则化的LSTM对于输入数据的要求较低，为化工实际生产过程的建模提供了更多可能。

3 结束语

笔者提出的基于L2正则化的LSTM辨识策略，能够有效地避免过拟合现象的发生，完成对非线性动态系统的辨识。 与BP、SVR方法相比，具有更快的收敛速度和辨识精度，在测试集上的误差控制在0.15%左右； 在训练集和测试集上的输出偏差控制在0.5℃以下； 拟合优度R2控制在3以内，表明对实际数据的动态走势预测良好。 从对不同数据集的辨识结果来看， 基于L2正则化的LSTM辨识策略能够降低对辨识数据的要求，对含有少量噪声的正常工况数据 （表1中的第1组数据）辨识时，仍然得到了良好的辨识效果，为离线辨识，得到“孪生”模型提供了可能。 将来应考虑利用其他优化算法对LSTM进行优化，以进一步提高辨识精度。