微波加热固体颗粒类矿物的过程控制分析
2021-03-19王银双曾德明
王银双 杨 彪, 杜 婉 成 宬 曾德明
(昆明理工大学a.信息工程与自动化学院;b.非常规冶金教育部重点实验室)
微波加热具有整体加热、低温快烧、高效节能、安全无污染和改善组织性能的优势[1]。 微波技术作为一种转化率高效、节能环保的技术,正适应当今世界的潮流。 随着人们对环保、能源利用要求的日益增强,对微波技术应用的研究也日趋深入。
微波加热系统中的温度控制具有非线性、大时滞和参数时变的特点[2],而且这类系统相对复杂,难以建立精确的温度数学模型,因此传统的PID控制很难达到最佳控制效果[3]。并且微波加热这一过程中存在纯滞后环节,很难使系统趋于稳定,不利于系统的性能控制。 为了弥补传统PID控制在应对微波加热这一非线性过程时的缺陷,笔者选择采用大林算法作为控制策略。
1 微波加热钛精矿过程控制分析
1.1 数据采集与分析
为了获得微波加热系统的传递函数,笔者采用实验的方法获得相关数据。 此次实验在昆明理工大学非常规冶金教育部重点实验室完成。 微波加热设备选择功率可调的箱式微波高温反应器[4],设置微波反应器输出功率为600W(其最大输出功率可达到6kW); 选取半径为47.5mm的球状钛精矿为被加热物料。实验每10s采集一次温度数据,具体见表1。

表1 实验采集的温度数据
根据表1可绘制出温度随加热时间变化的飞升曲线(图1)。
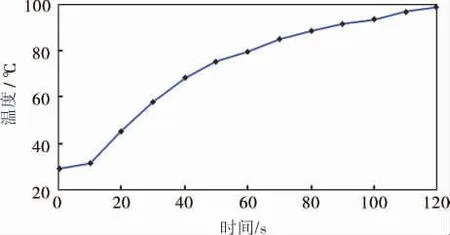
图1 微波加热钛精矿温度飞升曲线
根据图1分析被控对象(温度)的特征,可将系统传递函数近似看作一阶惯性纯滞后系统[5],用公式表示为:

式中 K——放大系数;
T——时间常数;
τ——迟延时间。
1.2 系统分析与模型确定
在工业控制流程中,大都是在控制对象上加入一个阶跃输入信号,根据阶跃响应来分析对象的动态特性。 为了得到精准的数学模型,则需要分别对放大系数、 时间常数和迟延时间进行求解。
1.2.1 求解放大系数
求解放大系数的公式为:
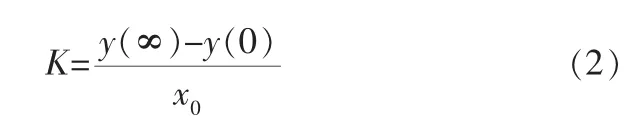
其中x0为对象输入信号的阶跃幅值,y(0)为初始设定值,y(∞)为阶跃响应的稳态值。
1.2.2 时间常数T和迟延时间τ的确定
采用两点法进行计算。 将一阶迟延对象(式(1))转换为:

其中,y(t)为阶跃响应,y*(t)为y(t)的量纲形式。
在阶跃输入作用下,y*(t)的解为:

先选定两个时刻t1和t2,其中t2>t1≥τ,从测试结果中读出y*(t1)和y*(t2)并写出下列联立方程:
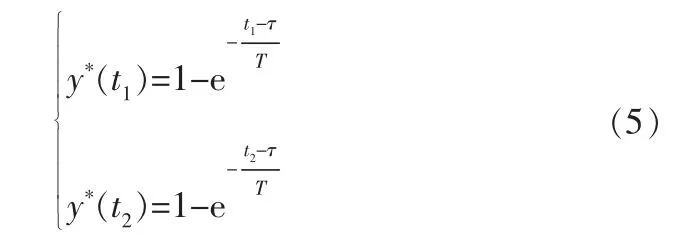
对式(5)两边取对数,并求出T和τ。
采用两点法, 根据表1中的数据可以求出微波加热系统的近似模型:

2 控制策略
通过对系统的分析和建模可得出, 传统的PID控制已满足不了微波加热物料过程的控制要求。 对于存在纯滞后环节的系统而言,若采用传统的PID控制,系统的超调量会增大,调节时间更长,系统的控制效果较差。 因此,为了消除纯滞后环节,笔者采用大林算法进行控制,并对两种控制方法的效果进行仿真对比分析。
大林算法是一种针对工业生产过程中含有纯滞后被控对象的控制算法[6,7]。大林算法的目标是设计一个合适的数字控制器[8,9],将一个惯性环节和一个延迟环节相串联构成闭环控制系统[10],即:

其中,Tτ为系统的时间常数;τ=NT′,N为正整数[11],T′为采样周期。
当闭环系统中带有零阶保持器时,传递函数为:

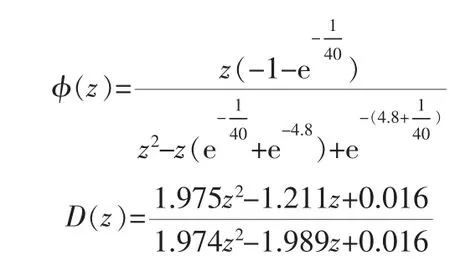
3 仿真与分析
3.1 传统PID控制仿真
通过MATLAB中的SIMULINK建模和软件环境进行计算机仿真。 温度设定值为100℃,初始值为29.1℃。 当比例系数Kp=1.8,积分系数Ki=0.061,微分系数Kd=8.5时,传统PID控制的仿真结果如图2所示。 其中上升时间为110.606s, 调节时间为319.697s,超调量为2.557%。

图2 传统PID控制仿真结果
3.2 大林算法控制仿真
仿真过程中温度设定值为100℃, 初始值为29.1℃。 仿 真 结 果 如 图3 所 示, 调 节 时 间 为237.879s,几乎无超调。

图3 大林算法控制仿真结果
3.3 仿真对比
对传统PID控制的参数取不同的值, 通过仿真实验将两种控制的仿真结果进行对比(图4)。
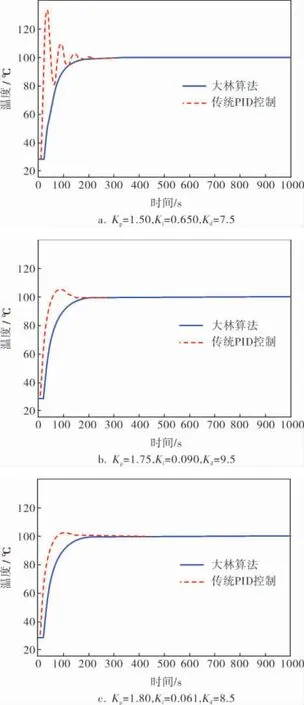
图4 仿真结果对比
根据3组不同参数的仿真图比较, 可以清楚地看出,大林算法控制比传统PID控制效果更优,具有更短的调节时间。 同时,选择不同的参数时,调节时间也会不同。 因此在实际应用中,需要根据系统的控制要求来对参数进行整定,获得最优的性能指标,达到最优的控制效果。
4 结束语
微波加热物料的过程是一个非线性、大时滞和参数时变的系统, 采用传统的PID控制满足不了该过程控制中所提出的要求。 因此,笔者采用大林算法进行控制,仿真实验结果表明,大林算法可以很好地消除纯滞后,并获得较好的控制效果。
