RV减速器传动系统动力学分析与试验研究

张圆东 肖正明 吴利荣

（昆明理工大学机电工程学院）

符 号 说 明

b——单齿变形区的宽度，b=12mm；

Cbx1qj——摆线轮1与曲柄轴阻尼系数；

Cbx2qj——摆线轮2与曲柄轴阻尼系数；

Cbx1s——摆线轮1与太阳轮阻尼系数；

Cbx2s——摆线轮2与太阳轮阻尼系数；

Chp1qj——行星轮1与曲柄轴阻尼系数；

Chp2qj——行星轮2与曲柄轴阻尼系数；

Chp3qj——行星轮3与曲柄轴阻尼系数；

Chps——行星轮与太阳轮阻尼系数；

Cis——输入轴与太阳轮阻尼系数；

Co——输出轴阻尼系数；

Cqjbx——曲柄轴与摆线轮啮合处的阻尼系数；

E——摆线轮与针齿的弹性模量， 本项目RV 减速器为

RV320E， 针齿和摆线轮的材料一样， 均为

GCr15，故E=2.06×105MPa；

F1——输入端等价啮合力；

Fi——摆线轮与针齿的啮合力；

Fmax——摆线轮在特定位置的最大啮合力；

Fo——输出端等价啮合力；

k0——平均啮合刚度；

k1——齿轮刚度谐波项；

k（t）——时变啮合刚度；

ki——摆线轮单齿啮合刚度；

km1——双齿啮合刚度；

km2——单齿啮合刚度；

K——啮合刚度；

K1——短幅系数；

K（t）——系统时变啮合刚度；

Kbx1qj——摆线轮1与曲柄轴刚度系数；

Kbx2qj——摆线轮2与曲柄轴刚度系数；

Kbx1s——摆线轮1与太阳轮刚度系数；

Kbx2s——摆线轮2与太阳轮刚度系数；

Khp1——行星轮1刚度系数；

Khp2——行星轮2刚度系数；

Khp3——行星轮3刚度系数；

Khp1qj——行星轮1与曲柄轴刚度系数；

Khp2qj——行星轮2与曲柄轴刚度系数；

Khp3qj——行星轮3与曲柄轴刚度系数；

Khpqj——行星轮与曲柄轴刚度系数；

Khps——行星轮与太阳轮刚度系数；

Kis——输入轴与太阳轮刚度系数；

Kit——摆线轮与针齿时变啮合刚度；

Ko——输出轴刚度系数；

Kqjbx——曲柄轴与摆线轮啮合处的刚度系数；

li——中心距；

m——啮合轮齿个数的最大值；

M——质量矩阵；

M1——输入端的当量质量；

Mbx1——摆线轮1的当量质量；

Mbx2——摆线轮2的当量质量；

Mhp1——行星轮1的当量质量；

Mhp2——行星轮2的当量质量；

Mhp3——行星轮3的当量质量；

Mo——输出端的当量质量；

Ms——太阳轮的当量质量；

n——啮合轮齿个数；

n′——啮合轮齿个数的最小值；

N——啮合总个数；

rc——摆线轮的有效半径；

rhp——行星轮的有效半径，rhp=5mm；

s——啮合线长度；

S——摆线轮上的位移；

t——啮合时间；

T——添加在摆线轮上的扭矩；

x¨——振动加速度；

x¨1——输入轴振动加速度；

x¨bx1——摆线轮1的振动加速度；

x¨bx2——摆线轮2的振动加速度；

x¨hp1——行星轮1的振动加速度；

x¨hp2——行星轮2的振动加速度；

x¨hp3——行星轮3的振动加速度；

x¨o——输出轴振动加速度；

x¨s——太阳轮的振动加速度；

X——振动位移；

Xbx1qj——摆线轮1与曲柄轴相对振动位移；

Xbx2qj——摆线轮2与曲柄轴相对振动位移；

Xhp1——行星轮1振动位移；

Xhp2——行星轮2振动位移；

Xhp3——行星轮3振动位移；

Xhp1qj——行星轮1与曲柄轴相对振动位移；

Xhp2qj——行星轮2与曲柄轴相对振动位移；

Xhp3qj——行星轮3与曲柄轴相对振动位移；

Xhps——行星轮与太阳轮相对振动位移；

Xo——输出轴振动位移；

Xs——太阳轮振动位移；

zp——啮合齿宽；

ω——角速度；

ωi——第i阶固有圆频率；

ωm——齿轮啮合频率；

φ——齿轮刚度谐波相位；

ε——重合度；

μ——摆线轮的泊松比，μ=0.3；

δmax——摆线轮的接触变形（最大应力处）；

Δ（φ）i——单齿啮合间隙；

φi——摆线轮与针齿啮合间隙；

θ——初始相位角；

Ψ——啮合角；

ψi——各构件相应的第i阶振型矢量。

工业机器人已在机械、航空及工业等领域广泛使用，随着工业机器人功能的改进，其优势逐渐显现出来。RV减速器新型两级小齿差速闭式行星减速器具有传动比大、传动效率高、承载能力强和回程误差小的优点，被广泛应用于工业机器人领域。 RV减速器在传动效率、传动精度和动态性能方面对工业机器人行业具有重大影响。 为了确保RV减速器的有效传输效率、承载能力和稳定性， 在工业机器人应用中充分利用一系列优势，对RV减速器传动系统的振动机理与特征进行分析研究十分必要，工程意义重大。

张大卫等基于Hertz公式和石川公式分别建立摆线轮传动副和渐开线传动副的啮合刚度模型，用惯性盘作工作负载，建立考虑负载影响的5自由度扭转动力学模型，并分析了曲柄轴的扭转刚度和齿轮的啮合刚度对系统固有频率的影响，得出双曲柄轴的扭转刚度主要决定系统的一阶固有频率［1］。 因此要提高RV减速器的性能，选择合理的曲柄轴材料和结构至关重要。 何卫东等利用石川方法和改进的弹塑性力学方法，获得了RV减速器主要影响因素的渐开线行星传动和摆线轮传动的等效扭转刚度数学模型［2］。 刘继岩和孙涛通过建立RV减速器的系统动力学模型，利用集中质量法推导出系统的动力学方程，并通过刚度分离方法将啮合刚度分解，同时将时变方程转换为具有固定参数的二阶微分方程，以获得整体固有频率［3］。 在此基础上，仍可保证整体速比。 增加针齿的齿数，发现固有频率随着齿数的增加而增加，并且使振动恶化。 韩林山和闪修洋考虑了接触变形、载荷、侧隙及制造等因素，用等效模型法分析主要部件的受力， 并根据D’Alembert原理建立传动系统的非线性动力学模型［4］。 以上研究大多数集中在固有特性方面，对振动响应的研究涉及较少，并且考虑因素也比较少。

笔者以RV320E 传动系统作为研究对象，建立扭转动力学模型，运用数值方法求解系统的固有特性和振动响应， 以期为RV减速器传动系统的动力学精细化建模和结果优化奠定基础。

1 RV减速器扭转动力学建模

笔者以RV320E传动系统为研究对象。 第1级是渐开线圆柱齿轮减速机构， 第2级是摆线轮减速机构。 主要构成部件有针齿壳、针齿、摆线轮、曲柄轴、输入轴、输出轴、渐开线行星轮及行星架等，其结构如图1所示。 太阳轮由电机驱动，行星轮由太阳轮驱动，这时它也沿着与太阳轮相反的方向自转。该速度用作第2级减速的输入速度。行星轮的转速由曲柄轴传递到摆线轮，摆线轮做偏心运动。 同时摆线轮和针齿围绕中心轴做旋转运动。 该旋转速度通过曲柄轴两端的轴承传递到行星架，最终达到减速的目的。

图1 RV减速器结构简图

笔者采用集中参数法进行建模。 将有旋转自由度的组件视为具有各自旋转自由度的集中质量。 RV减速器系统中的6个组件各自具有旋转自由度，将它们视为集中质量。 另外，渐开线行星轮和曲柄轴整体自转同时绕其轴线做轨道转动，可以认为是具有旋转和平动自由的集中质量。 摆线轮的运动类似于行星轮的运动，摆线轮可以被视为具有旋转和平动自由度的集中质量。 因此可以看出，RV减速器传动系统是具有8个旋转自由度的传动系统。 建立模型时根据传动系统中各个部件的啮合性质的不同，考虑影响因素也不同。

利用集中参数法建立的系统扭转动力学模型如图2所示。

图2 RV减速器扭转模型

根据上述所建力学模型，利用集中参数法建立RV减速器扭转力学方程表达式如下：

2 RV减速器传动系统固有特性分析

2.1 齿轮啮合刚度计算

用傅里叶级数表示渐开线齿轮时变啮合刚度k（t）为：

2.2 摆线轮的啮合刚度计算

摆线轮的单齿啮合刚度是与角度有关的函数，在计算整体啮合刚度时不能简单叠加单齿啮合刚度。 首先要计算出单齿的啮合刚度，然后将单齿啮合刚度转化为等效扭转刚度，最后将等效扭转刚度叠加就可以得到摆线轮的等效扭转刚度。

齿轮的啮合刚度随时间发生变化，动力学方程就变为可变参数微分方程，因此无法对方程直接求解。 可以使用分离刚度的方法，将啮合刚度分解为平均刚度和波浪刚度。 由于平均刚度对应于静态啮合期间啮合力产生的变形，因此可以从方程等式中消除静态位移。 这样该方程式被转化为固定参数的二阶方程，其中刚度波动作为周期激励，位移波动作为求解变量。

单个齿啮合刚度计算。 根据文献［5］可知，摆线轮单齿啮合刚度ki为：

设当摆线轮与针齿啮合时有i（i=n～m）个齿与针齿上相应的齿进行传递，则有：

根据文献［5］和RV320E相关参数可得啮合刚度K=1.569×108N/m。

根据所建立的RV减速器传动系统扭转动力学模型，忽略阻尼的影响，得到自由振动方程：

将式（12）代入式（11），整理后可得主振型方程：

RV传动系统动力学模型中的啮合刚度随时间变化而具有时变性，这使得固有频率的求解变得复杂。 为了简化计算，首先简化随时间变化的啮合刚度。 笔者使用的方法是在系统运动的周期中选择啮合刚度的平均值，以替换系统随时间改变的啮合刚度。 系统的固有频率仅与系统的刚度有关， 因此可以首先忽略系统中的齿隙和误差，以便获得仅含刚度的动力学方程。 其基本频率分量可以在求解时得到。

RV减速器传动系统中， 其振动模式分为3个类别：刚体运动模式、轮系振动模式和扭转振动模式。 求解系统固有频率见表1。

表1 RV减速器传动系统固有频率 Hz

RV减速器的每种振动模式都反映了系统的振动模式。笔者采用归纳法解释RV减速器传动系统的振动模式。 不同振型矢量元素和前7阶固有频率的系统振型矢量见表2。

表2 不同振型矢量元素和前7阶固有频率的系统振型矢量

图3是RV减速器的结构简化图。太阳轮、行星轮和摆线轮由椭圆形代替。 为了直观显示，将3个曲柄轴简化为1个，并用轴代替输出机构。 图4显示了每个阶次的振型。

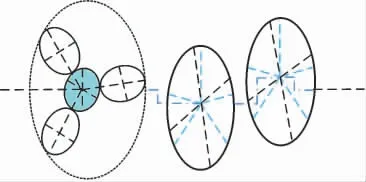
图3 RV减速器结构简化图

图4 不同阶次的振型

3 RV减速器传动系统振动响应分析

根据试验设备选取转速分别为500、800、1 000r/min，首先选取阻尼系数为0.03，运用龙格-库塔法对振动微分方程求解，得到关键部件的振动位移和速度。再改变阻尼系数为0.06，通过求解结果对比阻尼对其振动的影响。 图5为不同转速下的振动位移。

图5 不同转速下的振动位移

输入转速相同时， 太阳轮的振动比行星轮的大。 当输入转速为500、800、1 000r/min时，振动位移呈增大趋势，说明转速越高，振动位移越大，但影响不明显。 图6为不同转速下的振动速度。

图6 不同转速下的振动速度

求解结果表明： 通过使用Matlab的数值方法可以得到每个部件在额定速度下的振动位移。 根据振动位移图，可以清楚地看到振动位移的峰值按太阳轮、偏心轴、针齿和行星轮的顺序排列。 太阳轮、偏心轴、针齿和行星轮的振动位移为4.94、3.27、1.60、1.44μm。 太阳轮有相对较大的振动位移， 是因为太阳轮在计算过程中是作为输入轴，质量也相对较大，并且是系统第1级。 针齿的质量相对较小，在啮合过程中，摆线轮和多个针齿啮合，因此振动较小。 因此设计过程中要注意输入端的振动。 图7为不同转速下重要部件的振动位移有效值。

图7 重要部件振动位移有效值

由图7可以看出，在500r/min时各部件振动较为明显，应避免在实际工作条件下使用此转速和相近转速，以避免由于相对较大的振动而造成的损坏；同时在1 200r/min时各部件振动较小，符合设计要求。

4 试验验证

根据试验方案，使用已建立的测试台对系统的振动特性进行测试。 使用的传感器是加速度传感器。 首先收集到的是振动加速度信号，可以通过Matlab软件编程求解所需的振动速度。 因为RV减速器的结构是对称的，传感器的安装位置为减速器的顶部。 测试转速分别为500、800、1 000、1 200、1 500r/min。 图8为不同转速下的振动加速度。

试验结果表明： 以振动的峰值为研究参数，500、800、1 000、1 200、1 500r/min对应的加速度分别为0.12g、0.24g、0.59g、1.21g、1.60g。 可见，随着转速的增加，系统的振动加速度也呈现增大趋势。

图8 不同转速下的振动加速度

5 结论

5.1 在考虑时变刚度、 各级间耦合等因素下，建立RV减速器传动系统扭转动力学模型。

5.2 通过求解微分方程， 首先得到RV减速器传动系统的固有特性，并采用归纳法得出传动系统的振型矢量，通过振型矢量绘制在相应频率下的振型图。 其次得到各个部件在不同速度下的振动位移和加速度，在第1级中，太阳轮的振动大于行星轮。 不同转速下的同一部件随着转速的提高振动总体呈增大趋势，在500r/min时振动最为明显，在500～1 500r/min呈现波动增大的趋势。

5.3 转速和阻尼系数对系统振动大小有影响，转速越高，振动相对越大。 振动随着阻尼系数的增大而减小，而转速达到一定程度时对振动影响比较明显。