锂离子电池隔膜在压缩过程中的流固耦合效应

2021-03-19马德正李培超张恒运

储能科学与技术 2021年2期

马德正，李培超，张恒运

（上海工程技术大学机械与汽车工程学院，上海201620）

锂离子电池隔膜可使锂离子通过而不能使电子通过，从而达到隔离正负电极防止电极短路的作用。隔膜的性能直接影响着电池界面结构和内阻，从而影响电池容量、功率和循环寿命[1]。在电池充放电过程中电池内部组件体积变化会压缩隔膜变形，导致隔膜孔隙的收缩甚至关闭[2-3]。因此隔膜结构除了必须具备良好的化学稳定性、热稳定性和平整性之外还应具有良好的机械强度和结构稳定性[4-5]。随着近年来对锂离子电池充电速率的需求，对高应变率变形下隔膜应力机制的研究具有重要意义。

目前，已有不少通过实验方法对隔膜力学性能进行研究的工作。例如，Cannarella等[6]在对隔膜进行高应变率的压缩中观察到孔隙弹性效应所导致的速率依赖性，同时还发现碳酸二甲酯(DMC)溶液导致隔膜力学性能的降低。Yan等[7]建立了一种基于电容原理的薄膜位移测量装置，研究隔膜在厚度方向压缩下应力-应变曲线，发现隔膜厚度方向的压缩变形受到电极的影响。Chen等[8]对聚丙烯隔膜在不同电解液条件下的拉伸测试、热收缩、动态力学分析以及断裂进行了研究，发现液体电解质对高温下的尺寸稳定性和力学性能，特别是对聚合物隔板的抗裂性具有明显的负面影响。Yu等[9]对不同制造工艺下的隔膜进行了压缩实验，发现压缩是影响隔膜微孔结构、电解质吸收和电化学性能的关键因素。Ding等[10]通过二维小角X射线散射，二维广角X射线衍射和扫描电子显微镜研究了在不同温度下压缩的聚丙烯隔膜的应力应变行为和结构变化，发现压缩导致隔膜中孔隙率和孔连通性的降低将增加锂离子电池的内阻，并在高温工作时降低电流均匀性。

同时，也有一些学者利用数值模拟方法对隔膜的力学性能进行了研究。Xiao等[11]建立了一个多尺度模型对隔膜应力进行分析，结果表明隔膜中的应力随电池循环过程中的相变而改变。Shi 等[12]建立了袋式电池的多物理场模型对隔膜应力机制进行研究，发现当电池充满电时，隔膜中的最大应力总是出现在包裹着阳极的内角区域附近。Wu 等[13]建立了多尺度模型对隔膜原位应力进行分析发现，锂离子的嵌入和温度对隔膜应力的影响不是简单的求和。Gor 等[14]发现了压缩浸在流体中的隔膜时，其响应由聚合物骨架的黏弹性和孔隙弹性共同决定。

本文提出一种更能准确描述电池隔膜在压缩过程中流固耦合效应的模型，模型同时考虑了隔膜孔隙度和渗透率的动态变化，同时结合文献[14]中的实验数据和数值模拟结果对本文模型进行了验证；然后利用验证后的模型研究了隔膜内部孔隙压力、孔隙度以及渗透率的分布，并探讨了隔膜的渗透率、尺寸、杨氏模量、泊松比、液体体积模量以及黏度对隔膜流固耦合效应的影响。

1 模型

1.1 物理模型

隔膜在扫描电子显微镜下的微观结构如图1(a)[14]所示。当隔膜受压时多孔介质固体骨架受力变形，进而挤压孔隙内的电解液产生孔隙压力，孔隙压力会反作用于多孔介质固体骨架变形。因此，电池隔膜受到挤压变形的过程实际涉及多孔介质流体流动和固体变形耦合的机制。

本文以商用大孔半结晶聚丙烯隔膜(Celgard 3501)材料为例进行分析，模型由32 层直径为1 cm的隔膜样本堆叠而成[14]，如图1(b)所示。通过在模型上表面施加不同的应变率，研究隔膜分别被浸在水，DMC 以及电解液(1 mol/L LiPF6溶解于1:1 EC/DMC 混合物)条件下的应力-应变曲线。将有效杨氏模量定义为应力-应变曲线中2%应变对应的曲线斜率的大小[14]。仅对应变小于3%的情况进行数值模拟分析以确保隔膜材料处于线弹性变形阶段。本文模型采用了轴对称模型来进行分析，如图1(b)所示，其中H = 0.8 mm 和R = 0.5 cm 分别表示隔膜叠加后的厚度和半径。

图1 隔膜微观结构[14]和模型原理图Fig.1 Microstructure of the separator[14]and schematic diagram of the model

1.2 数学模型

由多孔介质有效应力原理[14]和有效应力应变本构关系方程[15]可得

式中，σ'ij为多孔介质固体骨架有效应力，Pa；E为多孔基质杨氏模量，Pa；v为多孔基质泊松比；εv为多孔基质体积应变，εv= ε11+ ε22+ ε33；p 为孔隙压力，Pa；b为Biot系数，定义如下[14]

式中，K和Ks分别表示多孔介质的体积模量和固体骨架的体积模量，K = E 3(1- 2v)，Pa。

孔隙压力p求解方程[16]如下

式中，Kf表示流体的体积模量，Pa；φ为孔隙度；κ为渗透率，m2；μ为黏度，Pa·s。

同时，模型中引入隔膜孔隙度φ 和渗透率κ 的动态模型[15]，表达式如下

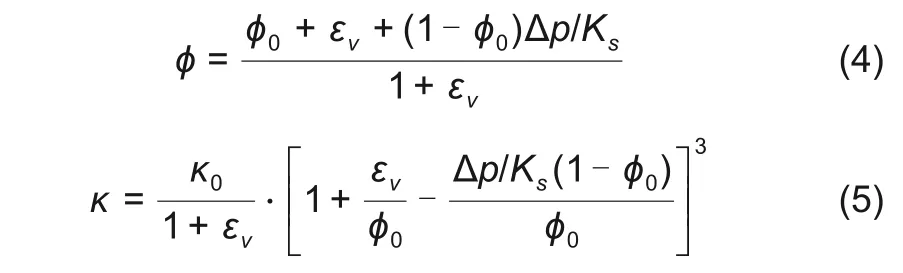
式中，κ0，φ0分别表示隔膜孔隙结构初始渗透率和孔隙度。

模型边界条件如下

式中，u 表示位移；ε 为拉力机施加的应变率，s-1。

文献[14]中实验是通过在模型上表面施加不同的应变率ε测得隔膜应力-应变曲线。在图1(b)模型中，孔隙压力仅随径向坐标r 变化，不随厚度z 和切向φ而改变，隔膜在z方向的应力为

实验中所测得有效杨氏模量可表示如下

2 模型参数

表1 给出了模拟涉及的参数。Gor 等[14]通过对干燥隔膜压缩实验数据的拟合得到了隔膜杨氏模量E随应变率ε变化的公式

式中，E0为隔膜在低应变率（ε = 10-5s-1）下的杨氏模量，常数CE= 23.2 MPa。

同时DMC 和电解液LiPF6对隔膜有软化作用，对浸在DMC和电解液LiPF6隔膜进行求解时分别对杨氏模量进行减小44 MPa 和36 MPa 的处理[14]。采用文献[14]中的方法对渗透率进行数量级估计，计算式如下

Gor等[14]观察到隔膜泊松比为v = 0，这与以往实验和文献结果[11-13]不符，因此在求解渗透率时使用文献[12]中泊松比值v = 0.35，求得渗透率值κ ～3.17× 10-17m2。

表1 模型参数Table 1 Model parameters

3 验证

使用COMSOL Multiphysics 5.4 软件中的达西定律和固体力学模块通过瞬态求解器对本文模型进行求解。图2 中，圆形点线图为实验数据[14]，矩形点线图为文献[14]的模拟结果。本文先用Gor 等[14]提出的模型和参数进行模拟，我们的结果与文献[14]模拟结果一致，如图2 中星形点线图所示。之后，我们对本文所建立轴对称模型进行求解，结果对应图2中三角形点线图。结果发现，模拟结果比文献中模拟结果更接近实验数据，且随着应变率的增大我们的结果更符合实验数据的趋势。当隔膜被浸在电解液LiPF6时的结果在高应变率时与实验数据差距明显，这可能是电解液体积模量未知用DMC 的值代替的结果。由图2(a)可知，当隔膜应变率小于10-2s-1时，隔膜强度主要受黏弹性的影响。当隔膜应变率大于10-2s-1时，隔膜强度同时受到骨架黏弹性和孔隙弹性的影响。

4 结果和讨论

下文我们以隔膜浸在水中为例，对本文建立的轴对称流固耦合模型进行结果讨论和参数分析。

图2 隔膜有效杨氏模量随应变率的变化Fig.2 Variation of the separator's effective Young's modulus with strain rate

4.1 孔隙压力分布

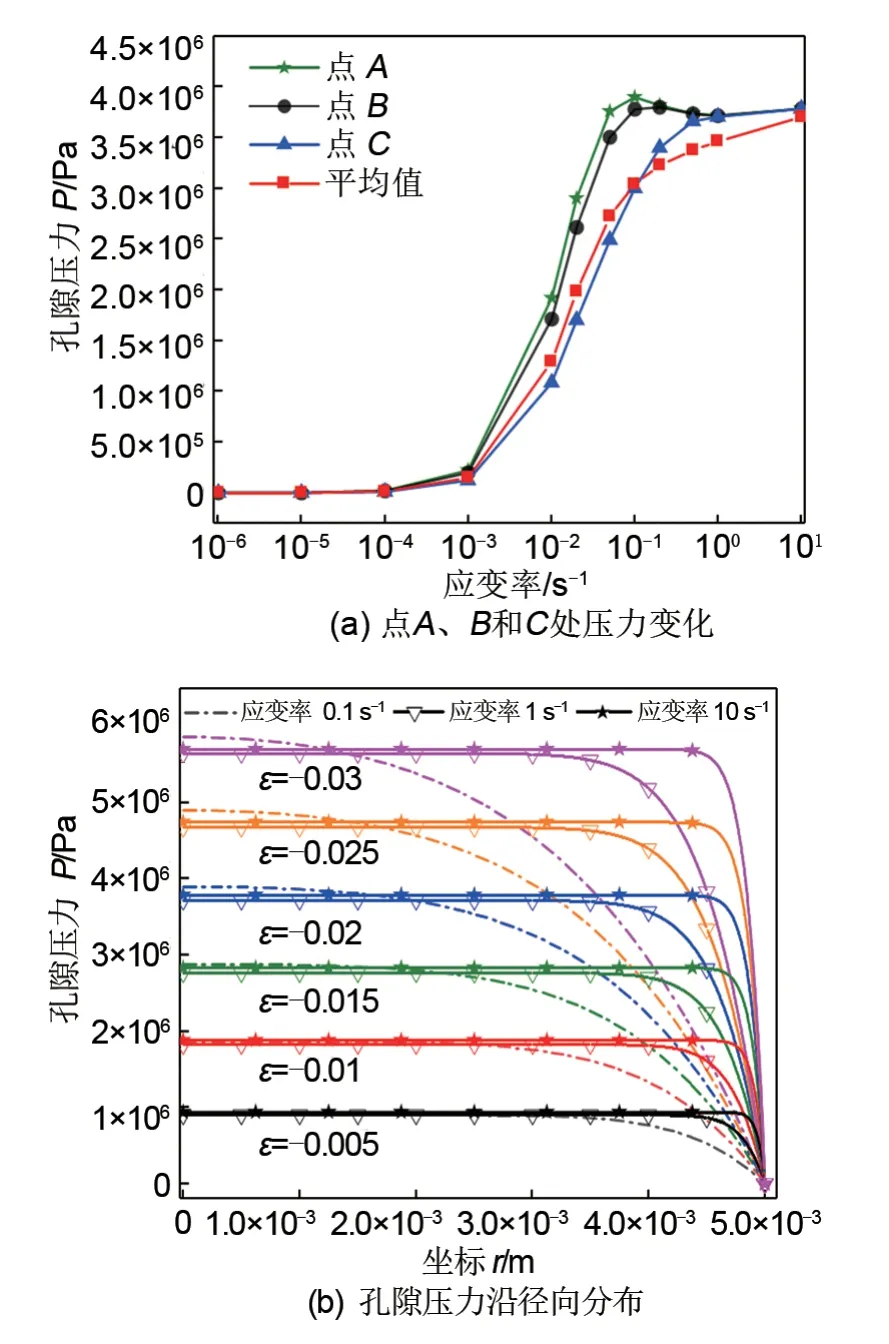
图3 孔隙压力的变化Fig.3 Evolution of pore pressure

图3(a)为点A、B 和C(图1)在εz= -0.02 时不同应变率下的孔隙压力随应变率的变化，矩形点线图为隔膜平面内孔隙压力的平均值的变化。结果发现，各点孔隙压力在低应变率下的值很小，随着应变率的增大而快速增加，这与实验中孔隙弹性响应明显的阶段对应。随后发现A 和B点处的孔隙压力随应变率的增加存在一个减小的趋势，C 点孔隙压力逐渐升高且增速降低，隔膜平面内孔隙压力的平均值在高应变率阶段曲线斜率降低(孔隙压力增速变缓)，这对应实验数据中在高应变速率下有效杨氏模量增速减缓阶段。图3(b)为不同应变率条件下隔膜内孔隙压力的分布随应变(时间)的变化。在应变率为0.1 s-1时孔隙压力沿坐标r 值的增大逐渐降低，并随应变的增加而逐渐升高。随着应变率的增加，隔膜内靠近对称轴处的孔隙压力会首先趋于均匀，这一区域随应变率的增加逐渐向外扩展的同时孔隙压力值缓慢增大。

4.2 孔隙度和渗透率变化

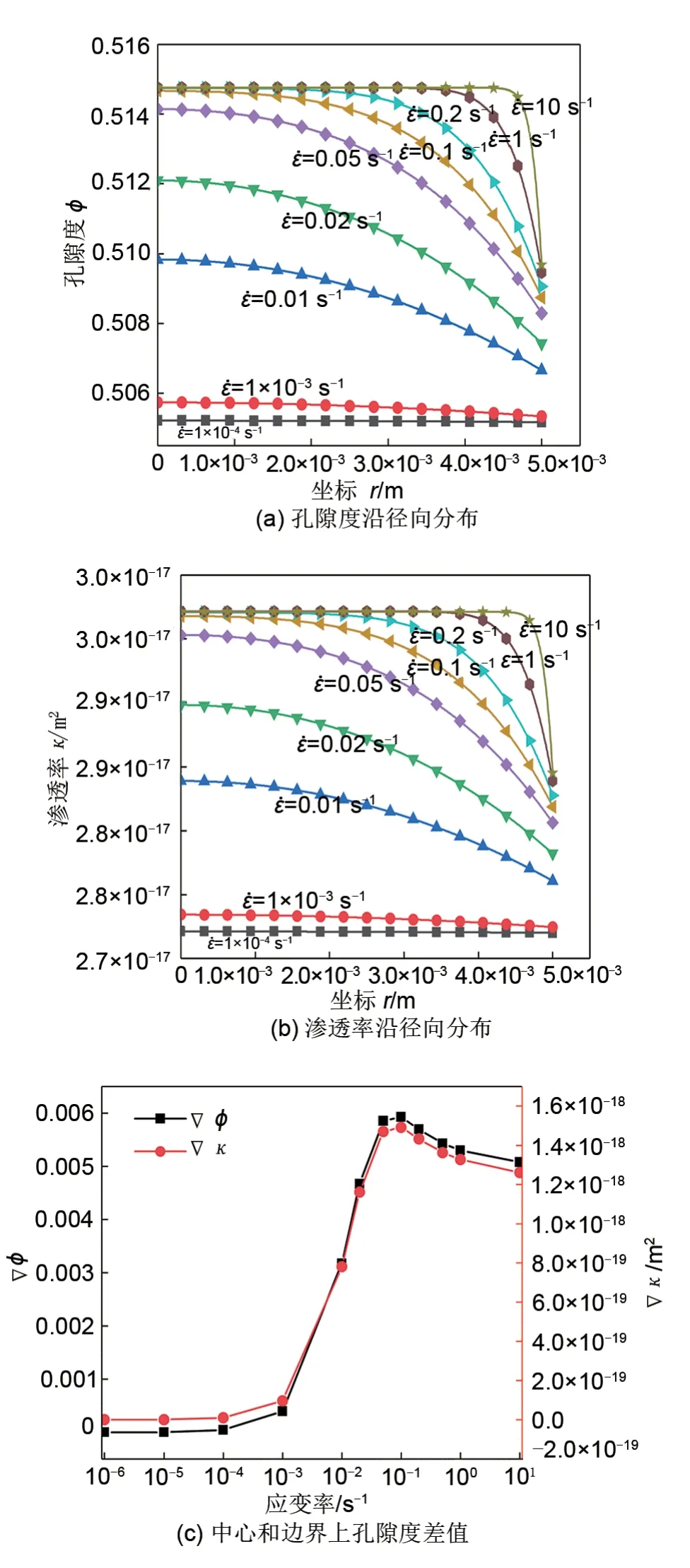
图4 孔隙度和渗透率分布Fig.4 Distribution of porosity and permeability

图4(a)和(b)分别为隔膜在不同应变率下εz=-0.02 时的孔隙度和渗透率沿径向坐标的分布。由图4(a)可知，当应变率较小时隔膜孔隙弹性效应不明显，隔膜孔隙度较小且沿半径方向的分布较均匀。随着应变率的逐渐增加，孔隙弹性导致隔膜中心孔隙压力增加，孔隙度将有所增加。在高应变率时，隔膜孔隙度将会率先在中心区域趋于均匀并沿径向方向逐渐向外延伸。观察图4(b)渗透率分布具有相同的趋势。电池隔膜孔隙度的分布不均将导致电化学反应的不均匀，进而导致电极受力不均匀。图4(c)为不同应变率下应变εz= -0.02 时隔膜中心和边界孔隙度和渗透率的差值曲线，发现这一差值在ε = 10-1s-1时达到最大，随后差异逐渐降低。此时，隔膜中心和表面孔隙度和渗透率差值的增大导致隔膜挤压液体流出受阻，致使隔膜中心处孔隙压力偏高(即图3 中隔膜中心区域孔隙压力在ε ＞10-1s-1时存在一个明显降低趋势)，这一影响随着内外孔隙度和渗透率差值的减小以及孔隙度和渗透率的增加逐渐消除。

4.3 参数分析

4.3.1 渗透率的影响

图5为不同渗透率下隔膜有效杨氏模量随应变率的变化。结果可知，随着渗透率的减小，有效杨氏模量产生突变时对应的应变率降低，即渗透率的减小导致隔膜孔隙弹性作用在低应变率时变得明显。这是由于多孔基质渗透率的降低导致液体不易流出，使流体在孔隙内产生孔隙压力。因此，应尽量选取渗透率较高的隔膜材料以抑制孔隙弹性效应。由图中曲线可知，不同渗透率在高应变率时对应的有效杨氏模量将趋近相同，并随应变率的增加缓慢增加。这一结果是由于在高应变率时孔隙压力在隔膜内部趋于均匀并缓慢增加造成的。同时观察到曲线在应变率为10-6～10-4s-1和1～10 s-1区间斜率相近，可知高应变率下隔膜孔隙弹性效应增速减慢。

4.3.2 厚度和直径的影响

图5 渗透率的影响Fig.5 Influence of permeability

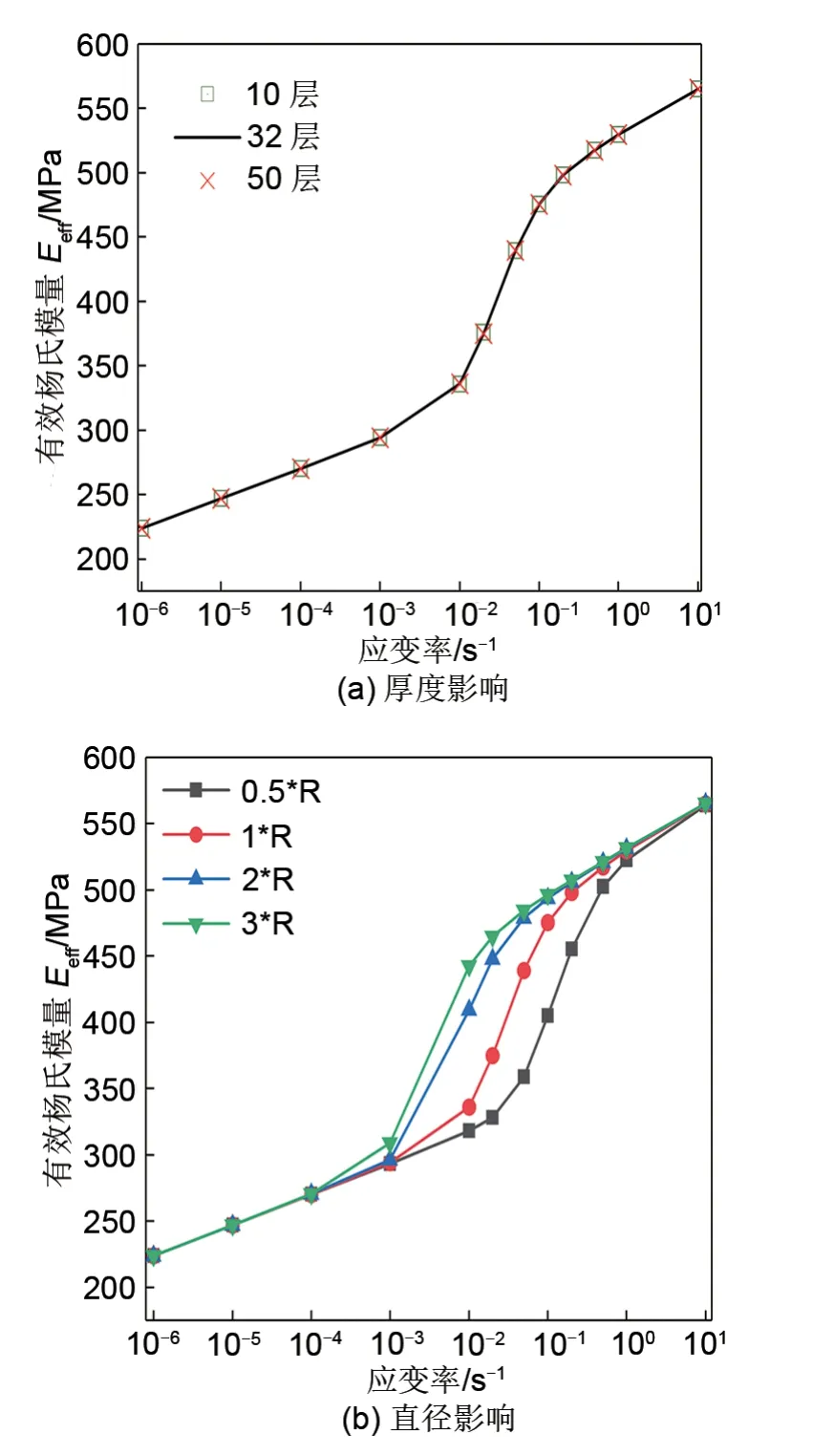
图6 隔膜厚度和直径的影响Fig.6 Influence of separator thickness and diameter

图6为厚度和直径的尺寸变化分别对隔膜孔隙弹性效应的影响。分析模型及边界条件可知隔膜内部流体孔隙压力和固体变形不随厚度方向变化，仅随径向坐标而变化，因此模型厚度变化对孔隙弹性无影响，如图6(a)所示。由图6(b)中有效杨氏模量随应变率的变化可得，随着半径的增大隔膜孔隙弹性开始响应时对应的应变率变低。但在高应变率下的内部孔隙压力分布变得均匀(如4.1 节所述)，不同直径下的有效杨氏模量值将会统一并随应变率增加而缓慢增加。

4.3.3 杨氏模量和泊松比影响

图7 中(a)和(b)分别为杨氏模量和泊松比的变化对隔膜在不同应变率下压缩有效样式模量的影响。由图7(a)可知，随着隔膜材料杨氏模量的增加，隔膜在不同应变率下的有效杨氏模量整体增加，对孔隙弹性响应时对应的应变率无显著的影响。由图7(b)可知，随着隔膜孔隙基质泊松比的增加隔膜在不同应变率下的有效杨氏模量将会减小，且泊松比越大将对有效杨氏模量的降低作用更明显。同时，通过曲线斜率的变化可知，当隔膜孔隙基质泊松比增加时，隔膜的孔隙弹性效应将会降低，因此，隔膜宜选用泊松比较大的材料。

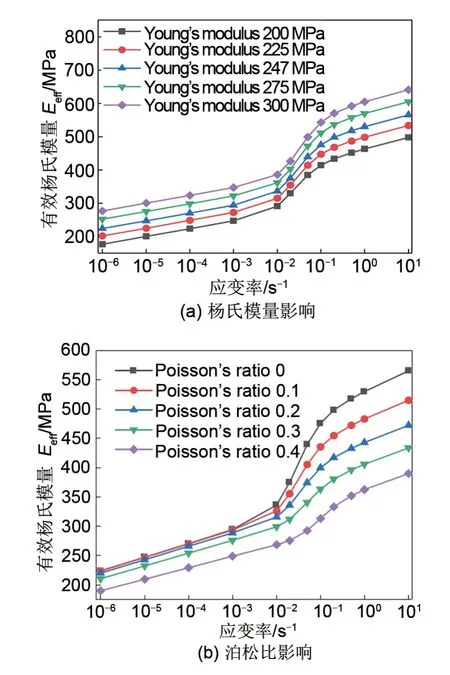
图7 杨氏模量和泊松比的影响Fig.7 Influence of Young's modulus and Poisson's ratio

4.3.4 液体体积模量和黏度的影响

图8(a)和(b)分别为液体体积模量和黏度对隔膜在不同应变率压缩下有效杨氏模量的影响。图8(a)可知，当液体体积模量增加时隔膜有效杨氏模量将会得到增强，即导致隔膜孔隙弹性效应增强。由于液体的可压缩性与体积模量成倒数关系，体积模量越大则液体更难被压缩，导致孔隙弹性会越明显。由图8(b)可知，液体的黏度越高将导致隔膜孔隙弹性更明显，孔隙弹性开始响应时对应的应变率也越低。这是由于液体黏度的升高导致液体的流出受阻碍，孔隙压力增强所导致。因此，应选用液体体积模量和黏度较小的电解液材料。