逗号刮刀涂布流场理论分析与数值模拟
2021-03-19梁卫华吴大勇舒均国
梁卫华,吴大勇,舒均国
(1中国科学院理化技术研究所,北京100190;2湖南中锂新材料有限公司,湖南 常德415001)
20 年来,锂离子电池逐步成为应用最广泛的储能器件,为消费电子产品和电动汽车提供动力。中国已建成完整的锂离子电池产业链,根据中国电子显示:2019 年中国锂离子电池产量为157.2 亿只,同比增长12.4%;按容量计算,锂离子电池产量148.0 GW·h,同比增长19.2%。其中,动力电池产量为85.4 GW·h,同比增长21%;消费型电池产量56.2 GW·h,同比增长15.4%[1]。中国已经成为世界上最大的锂离子电池生产国,且市场需求仍在不断扩大[2]。虽然我国已经在锂电池制造工艺和装备制造业方面都取得了长足的进步,但是在涉及卷对卷制造工艺领域的基础研究几乎是停滞的。在锂电池极片生产过程中应用卷对卷工艺包括涂布、辊压、分切、卷绕等工序。其中涂布工艺,涉及涂布浆料的均质与输运、流体力学和表面张力控制下的润湿与铺展、浆料的薄膜干燥与固化等化工单元过程和多台电机电气控制和基膜张力控制等单元控制过程。因此涂布工序被认为是锂电池生产中最为复杂和重要的工序。作为生产极片的工程技术人员,即使并不需要深入了解各种涂布设备制造的技术细节,至少也需要掌握各种涂布参数的意义和设置方法。但是,各种关于涂布技术的专业书籍和文章,由于涉及流体力学,阅读起来深奥难懂,致使我国产业界理论与技术水平和美国、日本等存在巨大差距。
涂布有多种方式,如顺辊涂布、逆辊涂布、刮刀涂布、挤压涂布、坡流涂布、凹版涂布等。基于涂布浆料的性质和涂布厚度精度的要求,往往可以选出2~3 种涂布方法。例如,适用于电池极片涂布的方法有刮刀涂布、挤压涂布等。条缝挤压涂布是一种重要的涂布方式,其涂布量由计量泵设定,对涂布厚度/面密度的控制比较精确[3],生产效率也很高。因此,条缝挤压涂布正逐渐替代逗号刮刀转移涂布,成为锂离子电池极片制造的主流方法。但是,条缝涂布也有不足,即高速工作时不能进行间歇涂布留出焊接极耳的空白。逗号刮刀转移涂布是另一种应用广泛的极片生产方式[4](图1),它的结构简单,制造成本较低,清理方便,特别适用于极片的分段涂布,因此在消费电子型锂电池极片制造和超级电容的极片制造中,仍被普遍采用。但是在锂电池极片涂布生产过程中,操作工人通常需要凭借经验多次调整涂布缝隙H0来获得需要的涂布厚度和面密度,难以避免的试涂工作浪费了大量的物料并降低了生产效率。
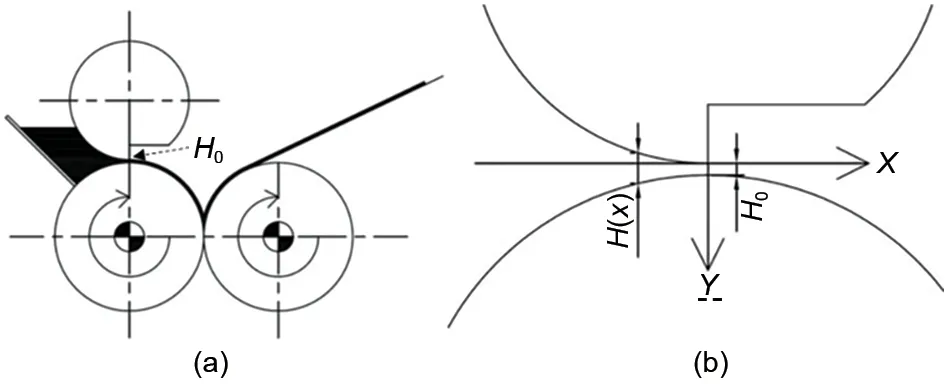
图1 (a)逗号刮刀转移涂布;(b)涂布缝隙放大图及坐标系Fig.1 (a)Schematic diagrams of comma-roll coating;(b)enlarged view of coating gap and coordinate system
从20世纪80—90年代起,国际上涂布技术的研究主要集中在顺流对辊涂布和逆流对辊涂布方式上[5-6],而关于逗号刮刀涂布的理论分析和实验研究较少。近年来,包能胜等[7-8]从雷诺润滑方程出发,结合涂膜的成型机理,建立双辊涂布的理论模型求解涂布厚度并与流体仿真结果进行了对比得到比较吻合的结果,并预测了双辊涂布的涂布厚度。刘正士等[9]从材料力学的角度出发计算了流场压力引起刮刀变形对涂布横向精度的影响。不过,该研究没有求解关于涂布最关心的问题——涂布厚度/面密度。本文作者认为,非常有必要针对逗号刮刀涂布建立模型,开展理论分析并结合流体力学专业软件进行数值模拟;探究刮刀辊、涂布辊径、缝隙高度等上游形状因素对流场和涂布最终厚度影响,导出涂布湿厚度与涂布缝隙的关系式,将模拟数值与理论值、实际涂布结果相对照,从而揭示涂布湿厚度与涂布刮刀缝隙之间的关系,提高涂布工艺的效率和水平。
根据表观黏度与剪切速率的关系,常把涂布浆料分成3种:剪切变稀型流体、剪切变稠型流体和牛顿型流体。锂离子电池极片涂布浆料是复杂的混合体系,包括溶剂、黏合剂、活性材料和导电添加剂等。它通常表现为非牛顿剪切变稀材料,其流变特性包括黏度剪切变稀、黏弹性、屈服应力和时间依赖性[10]。涂布过程是一个连续稳态过程,浆料的黏弹性、屈服应力等对涂布的影响较小,可忽略不计。浆料加工设备和工艺条件会影响浆料的黏度。当浆料所含黏结剂较少时,呈现牛顿型流体特性;由球磨机和3D 混合器制备的浆料也呈现牛顿型流体特性[10-11]。由于浆料体系实际情况比较复杂,所以在涂布研究和涂布装置的设计中往往将浆料视为均质流体。对于非牛顿流体的浆料也可以在一定的剪切率范围内将其近似为牛顿型流体,取特征剪切率下的黏度进行分析和计算。这种处理方法在文献中已有报道[3,8,12-13]。
1 刮刀涂布理论分析与求解
1.1 刮刀涂布数学模型的推导
逗号刮刀转移涂布如图1(a)所示,常用于锂电池极片涂布。涂布辊以速度U*顺时针转动将涂布浆料带出刮刀缝隙H0在涂布辊上形成稳定涂布湿厚度Hw;橡胶背辊顺时针转动并与涂布辊负间隙接触,将浆料完全转移到铝箔或铜箔上。上下移动刮刀可以改变涂布缝隙H0,从而改变涂布最终湿厚度Hw。如何确定H0与Hw的关系,是技术人员十分关心的重要问题。
特定浆料涂布的特性是流体力学研究的范畴。纳维-斯托克斯方程是流体力学的基本方程
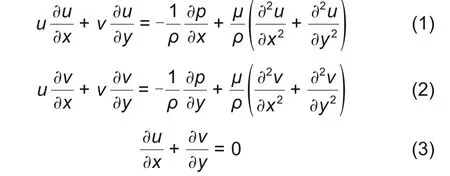
式中,u为流体在x方向的速度;v为y方向的速度;p为流体静压力;μ和ρ分别为流体的黏度系数和密度。
根据远场理论,远离刮刀缝隙处的流场流动对刮刀缝隙处的流动影响很小,可以忽略不计。因此将研究重点放在逗号刮刀涂布缝隙附近的区域,建立以逗号刮刀圆弧与垂直线交点为坐标原点、坐标体系如图1(b)所示的研究区域。在该区域内,即刮刀-涂布辊缝隙范围内,按雷诺润滑理论Y 方向的速度很小可以近似v=0,从式(3)可得∂u/∂x=0、∂2u/∂x2=0,代入式(1)、式(2)中,得到

式(4)和式(5)即为一维形式的雷诺润滑方程,由此两式可知流场压力只关于x 的一维函数p(x),速度u是只关于y的一维函数u(y)。
对式(4)进行y坐标方向上的一次积分
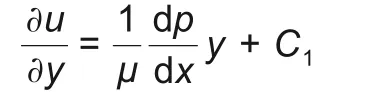
二次积分为
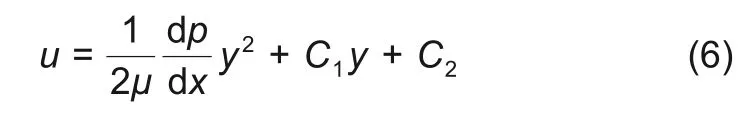
式中C1和C2未知。这时需要引入边界条件:刮刀圆弧处速度为零即y=0 时u=0;涂布辊速度为U*,即y=H(x)时u=U*,U*为涂布速度。
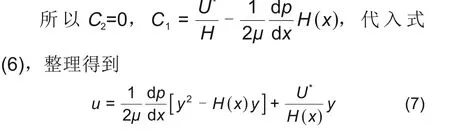
式中H(x)为刮刀与涂布辊之间的缝隙高度,是关于x 的形状函数。在图1(b)坐标体系下,定义刮刀缝隙最小高度为H0,则刮刀与涂布辊之间的缝隙高度H(x)为

式中当量半径R=RcRr/(Rc+Rr),式(7)是关于y的显函数,同时也是关于x 的隐函数,因为式中dp/dx和H(x)都是关于x的函数。目前来看,dp/dx关于x的函数是未知的。此时需要引入系统的质量守恒定律,假设Q是涂布浆料在单位宽度上的体积流量,那么沿x方向的流量是恒定的都为Q。

式中,Hw为最终涂布湿厚度,未知。将式(7)代入式(10)中
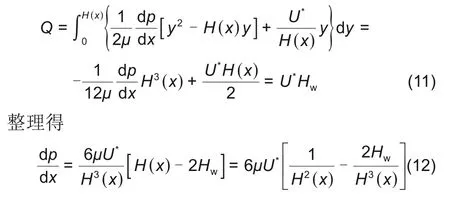
至此,式(12)推导出了基于雷诺润滑理论的刮刀缝隙涂布理论模型。
1.2 理论模型的求解
结合边界条件例如压力导数边界条件或压力边界条件和几何形状函数H(x)可以对上述模型进行求解,最终求出最终涂布厚度Hw。如图1所示,刮刀和涂布辊的左侧安装有涂布料槽。在进行刮刀涂布的过程中,料槽内充满涂布浆料,并且人工或液面跟踪系统保持涂布液面稳定。又因为在式(1)~式(3)中忽略重力因素对流场的影响,可以假设在-∞≤x≤0区域内充满涂布浆料。那么在x=-∞处,压力为外界空气压力,即

在x=0处,压力为外界空气压力。

将式(9)代入式(12)整理得
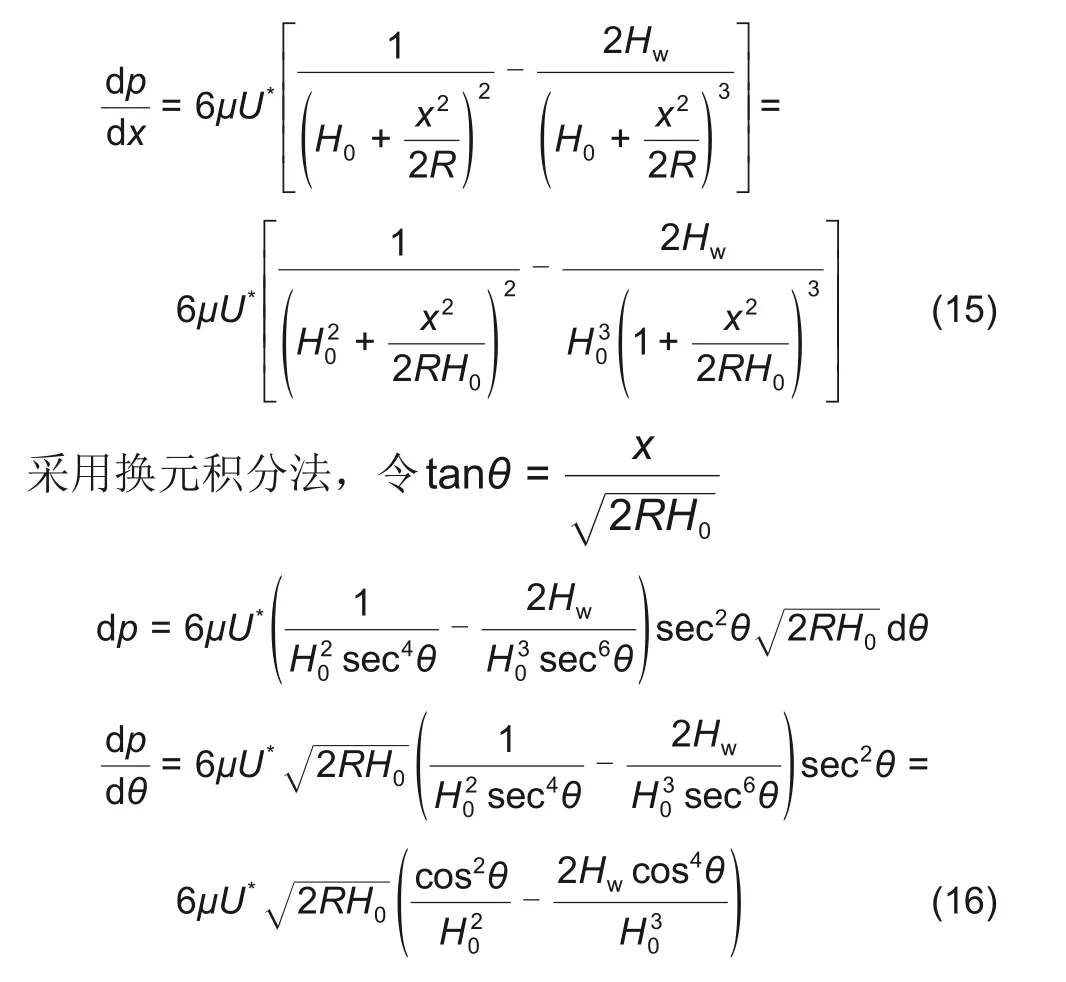
对式(16)进行积分,

在上述边界条件中,假设p(-∞)=0,显然这个假设与涂布料槽的实际情况不符。那么提出另外一种假设,边界条件为x=-R 当量半径处的压力为零,即

其中x=-R=-RcRr/(Rc+Rr),该点所处流场的位置见附录1。

为简化起见,令R/2H0=K,这是一个关于流场轮廓几何形状的参数,得

至此推导出了基于雷诺润滑方程理论的逗号刮刀几何形状参数对涂布厚度影响的关系式(23)。在已知刮刀辊、涂布辊当量半径R和刮刀缝隙H0时,可以通过该式计算最终涂布湿厚度Hw。另外在计算出Hw/H0后,可以得到流场压力随位置θ变化的函数
其中式(23)与文献[14]中的刮刀涂布厚度公式特定条件下(刮刀倾斜角度为0)得到的公式相同,只是我们的推导过程主要针对逗号刮刀,而不是文献[14]中的通用型刮刀。
2 基于Fluent 软件的逗号刮刀流场模拟
上述的刮刀涂布理论分析与求解是建立在刮刀缝隙附近小区域内,流场符合润滑理论假设的基础上,并在设定p(0)=0和p(-R)=0的边界条件下求解得出的。进而,我们希望利用专业软件建立流场范围更广、更接近逗号刮刀涂布流动实际情况的2D模型;通过设定适当的边界条件,用CFD 方法求解流场模型。可以通过两者结果的比较来判断刮刀涂布理论边界条件是否合适,并分析前者的适用范围。因此,采用Fluent软件进行了逗号刮刀流场模拟。对逗号刮刀流场进行流体力学数值模拟计算,首先使用Fluent 软件的网格模块Gambit 建立浆料料槽和刮刀涂布辊组成的2D 模型,并定义边界条件。如图2涂布辊边界条件定义为moving wall,逗号刮刀边界条件定义为wall,料槽顶端边界条件设为Pressure-inlet,刮刀缝隙出口的边界条件设为Pressure-outlet,其他的边界设为wall 条件。因为不考虑重力对涂布厚度的影响,所以在操作条件中未激活重力因素选项。
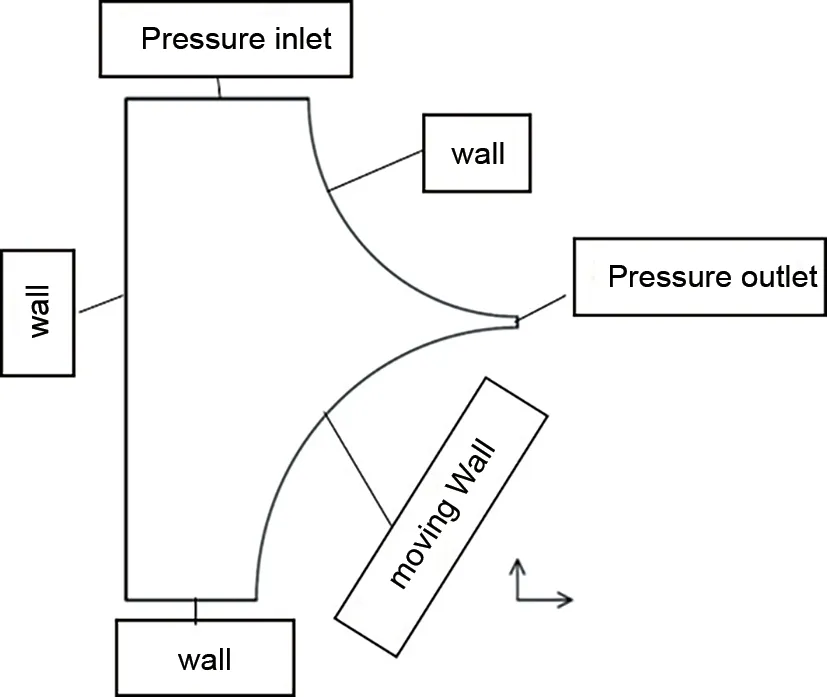
图2 刮刀涂布流场边界条件Fig.2 Physical model of 2D and boundary conditions
其次,是2D 模型网格的划分。以涂布辊半径Rr=20 mm,刮刀半径Rc=20 mm,涂布缝隙H0=0.2 mm 为例,采用Submap 方式,单元为Quad型,对2D 区域进行网格划分。其中,在压力出口处进行了细化,划分数为40,结果如图3所示。其中Cell 数量22400 个,Face 45200 个,Node 数量22841 个。最小网格面积5.0×10-6m2,最大网格面积5.45×10-4m2。网格验无关性验证的工作证实在压力出口处划分大于等于40,整体面网格大于等于45200个后压力出口处的流量已经不随网格数量的变化而发生变化了。
再者,设定涂布浆料密度ρ=1000 kg/m3,浆料黏度μ=5 Pa·s,涂布速度U*=0.1 m/s,料槽顶端边界条件设为Pressure-inlet,刮刀缝隙的边界条件设为Pressure-outlet,两者的数值都设为0。计算该区域的雷诺数Re=H0U*ρ/μ=0.004,因此在Fluent V6.3.26 软件中,采用层流模型,忽略重力因素,用有限体积法求解控制方程,选择采用压力隐式稳态定常求解器。控制方程压力离散采用标准式,动量离散采用一阶迎风格式,压力速度耦合方程组采用Simple 算法及欠松弛因子迭代求解。
迭代次数及收敛标准:本算例中采用,连续方程和速度方程的残差要求控制在小于10-6和10-7迭代次数为6613 次。计算区域和刮刀缝隙区域流函数分布如图4所示,全流场内的压力云图和刮刀缝隙区域压力云图如图5所示。在远离狭缝的大部分区域内压力分布在-1.20×10-3~1.14×10-3Pa之间,近似为0。仅在距狭缝出口5 mm 范围内,压力先显著上升再急剧下降,表现为只与x相关的一维函数p(x)几乎不随y 变化。这与前文雷诺润滑方程的推论相同。需要指出的是,在图5中负压出现在涂布辊刚刚进入料槽处,液体速度急剧上升引起压力下降,成为全流场静压最低点。压力出口处的速度沿y轴分布如图6所示。
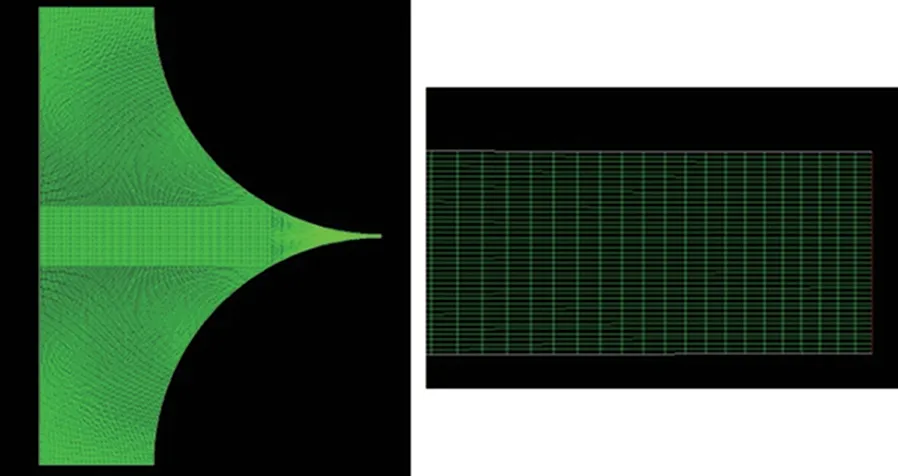
图3 刮刀涂布流场的网格划分Fig.3 Grid of comma-roll coating model
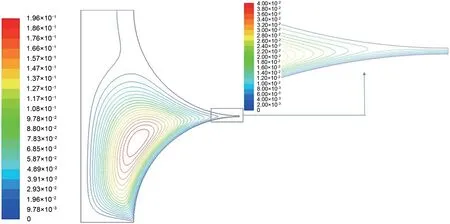
图4 逗号刮刀流场的流函数Fig.4 Stream function distribution
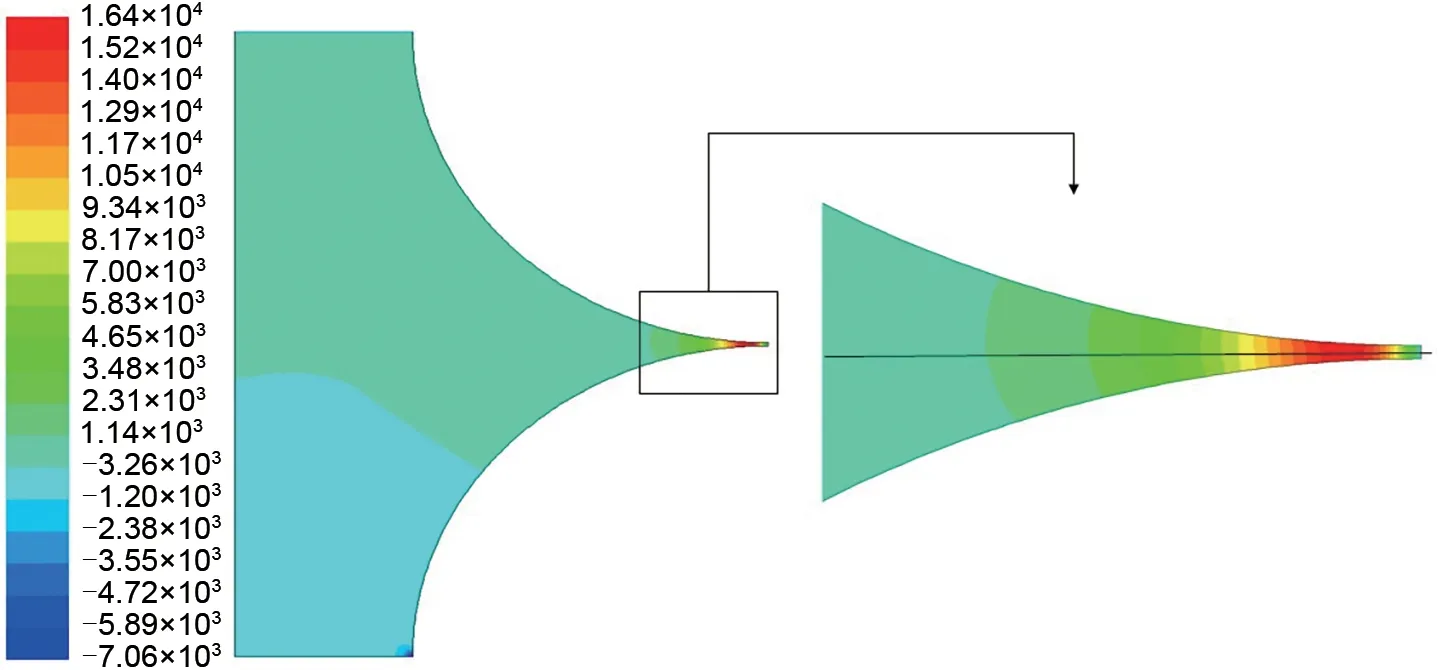
图5 刮刀缝隙处的压力分布Fig.5 Pressure distribution at coating gap
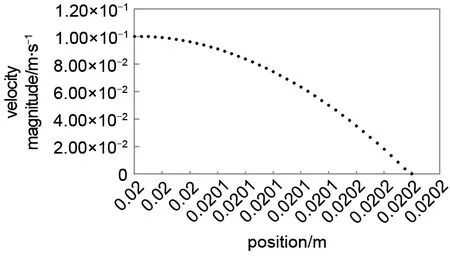
图6 缝隙出口截面(x=0)速度曲线Fig.6 Velocity distribution curve at x=0
最后,根据计算结果中涂布缝隙H0处输出的质量流量m=0.013280711 kg/s,计算涂布湿厚度与涂布缝隙的比值Hw/H0=m/ρU*H0=0.6640。
采用与以上算例类似的方法和过程,分别用软件模拟了不同辊径、缝隙高度、黏度和速度下流场情况,并计算Hw/H0数值,结果列入表1、表2和表3。
3 结果与讨论
3.1 刮刀缝隙带出率Hw/H0与几何形状参数K 的关系
通过对逗号刮刀涂布流场雷诺润滑理论建模和求解,得到了关于刮刀辊、涂布辊辊径、缝隙高度等上游形状因素对流场和涂布最终厚度湿厚度的关系式(23)。求解公式(23),得到了K与Hw/H0的函数关系(图7),并将表1 中流体模拟结果Hw/H0引入图7。结果表明,逗号刮刀涂布的湿厚度Hw与刮刀缝隙高度H0呈正比关系,同时受到上游当量半径与缝隙高度比值R/2H0=K 影响。K 越大,Hw/H0的比值越大。当K 趋向于+∞,即涂布缝隙趋近于0 时,Hw/H0→2/3。这意味着牛顿流体的逗号刮刀流场流出率的极限值Hw/H0=2/3。
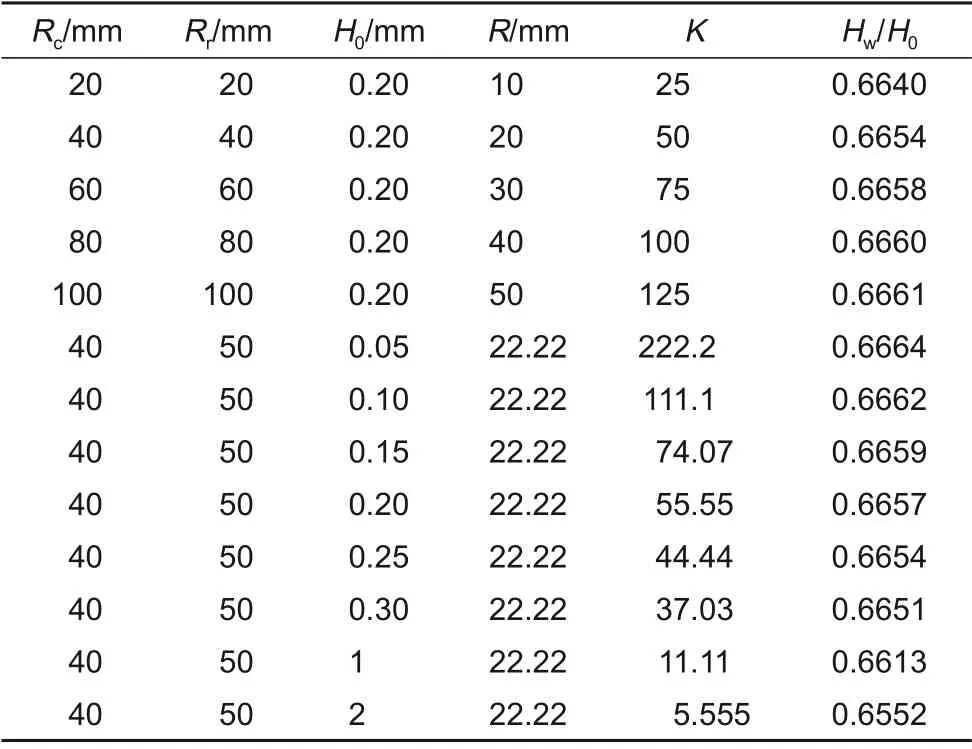
表1 辊径大小和缝隙高度对涂布厚度影响Table 1 Simulation results of different geometric parameters

表2 浆料黏度对涂布厚度的影响Table 2 Simulation results of different viscosity

表3 速度对涂布厚度的影响Table 3 Simulation results of different velocity
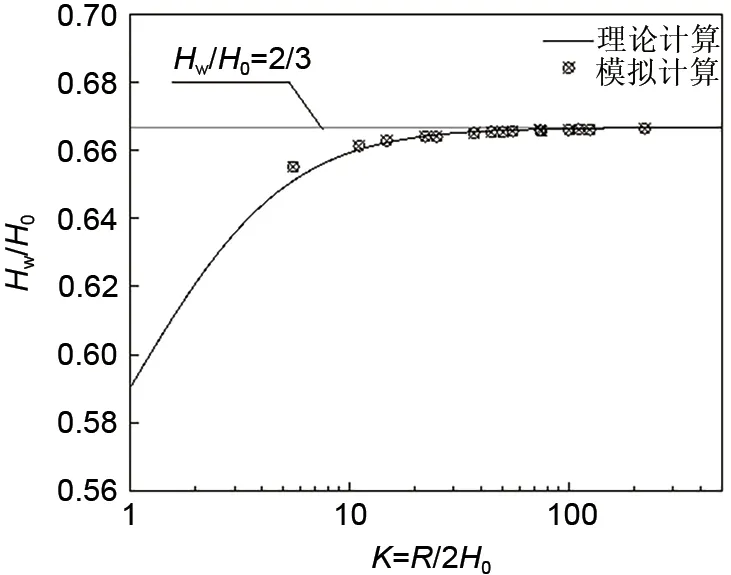
图7 Hw/H0关于几何参数K的函数图Fig.7 Comma roll coater flow rate predicted by lubrication theory,with comparison to numerical model
由于在实际应用中K=R/2H0的取值范围一般在10~2000范围内,所以Hw/H0的取值范围,多在略小于2/3 的0.66 附近。图7 所示,润滑理论计算结果和表1 中2D 流体力学软件模拟计算的结果在K值(10~2000)范围内高度吻合,说明逗号刮刀涂布模型是合理的。涂布工程师和操作技术人员可以使用该公式来设定合适涂布间隙H0来进行第一次试涂。
3.2 流场中的压力分布
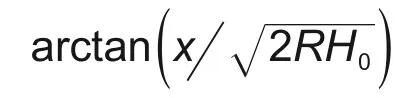

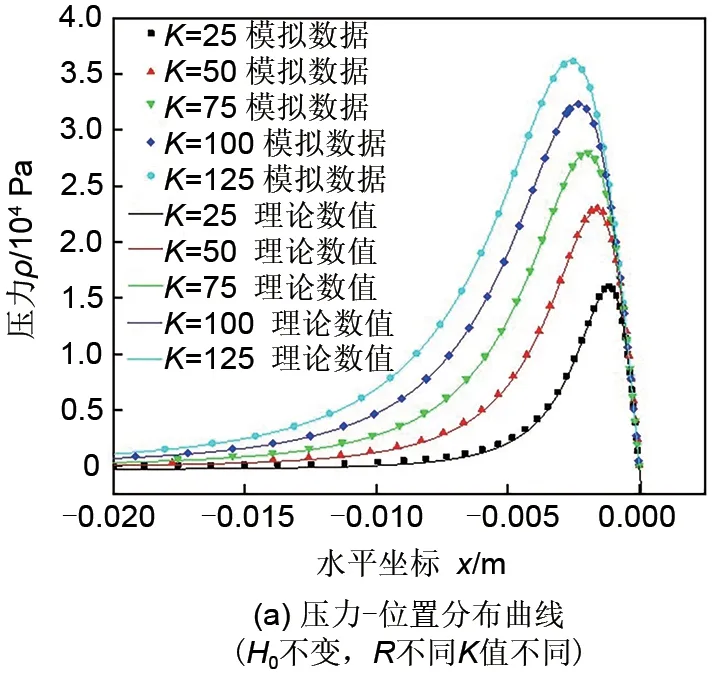
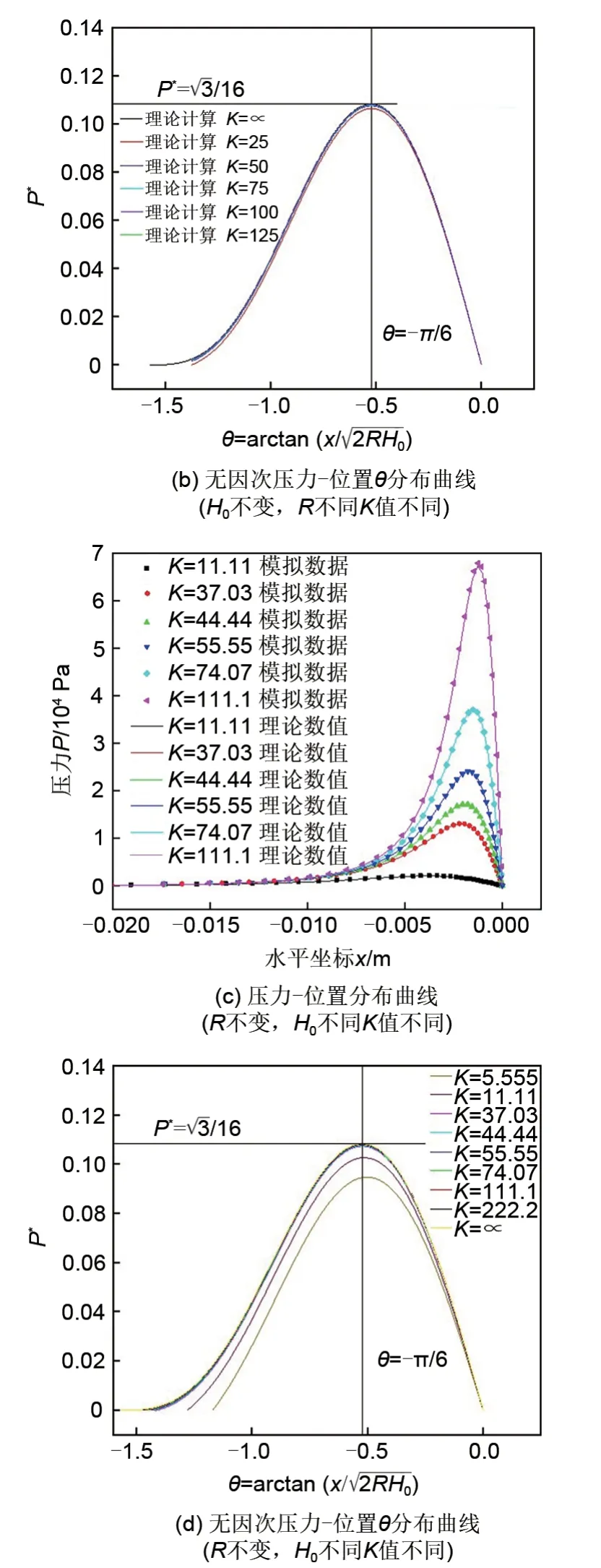
图8 不同K值时流场压力与位置关系图Fig.8 Relationship between flow field pressure and position at different K values

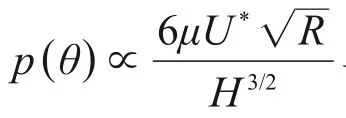
理论推导过程中边界条件p(-R)=0的假设是否成立,可以通过软件计算来验证。在表1不同几何参数的软件模拟结果压力分布云图(图5)中取坐标(-R,0)点的压力p(-R,0),代入式(25),考察此处的无因次压力P*(-R,0),结果列于表4。可见,除了K=5.55的无因次压力P*(-R,0)=0.0154外,在其他K值条件下P*(-R,0)与P*max相比都可以近似为零。因此,p(-R)=0的边界条件假设基本合理。

表4 不同几何参数K条件下的-R处的无因次压力Table 4 Dimensionless pressure at point of(-R,0)
3.3 浆料黏度和涂布速度对涂布厚度的影响
由式(23)可知,作为牛顿流体涂布浆料的黏度对涂布厚度没有影响。这一点通过Fluent软件模拟也得出相同的结论,表2 中浆料黏度在0.1~10 Pa·s 的变化,引起的厚度变化不到千分之一,说明浆料黏度变化对厚度几乎没有影响。同样地,在Fluent模拟结果中(表3)涂布速度从0.005 m/s变化到0.4 m/s,涂布厚度只有万分之一的变化。这表明速度对涂布厚度没有明显的影响。在式(11)中涂布流量与涂布速度U*和dp/dx有关
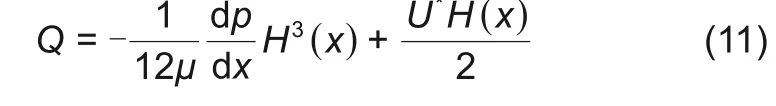
把式(16)代入(11)中,则可以消除黏度项μ。因此,涂布厚度与浆料黏度并不相关。又因为Hw=Q/U*,在计算过程中又消除了涂布速度U*。因此,涂布厚度也不受涂布速度大小的影响。
3.4 重力作用产生的水力压头对涂布厚度的影响
在理论模型的建立和求解中忽略了重力作用对涂布厚度的影响。这是因为刮刀涂布方向为水平方向,与重力方向不一致,其水力压头沿水平方向x的偏微分∂pg/∂x不能求出解析解。为了进一步分析重力作用对涂布厚度的影响,将上述公式中的静态压力p 由其静压和水头压力组成的等效压力pe=p+pg代替,其中在刮刀缝隙处x 轴的水头压力pg=ρgRc,Rc为刮刀辊半径。考虑重力因素后,式(17)的边界条件应该改为p(θk)=ρgRc和p(0)=0。求解该方程可得

式(27)中第1 项与式(23)相同,是未考虑重力时的涂布带出率;第2 项为狭缝进出口水头压力差对涂布厚度的影响,定义为Δ Hg。因为θk=arctan( - R 2H0)∈(-π/2,0),所以第2 项分母为负值。涂布厚度在考虑水力压头时会比不计水力压头时有所增大。根据式(27)计算如表1 的各参数时水力压头对涂布厚度的影响ΔHg,见表5。
同理也可以计算出表3 和表4 条件下水力压头对涂布厚度的影响,见表6。
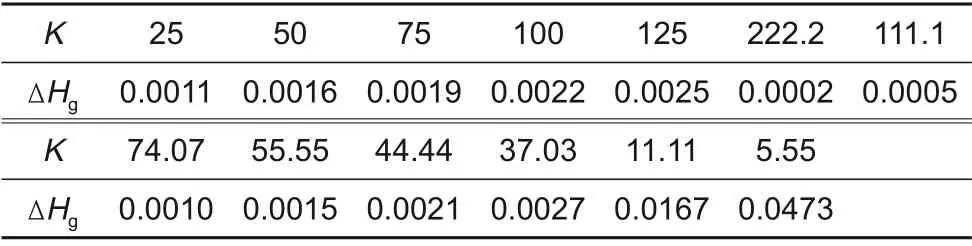
表5 不同几何参数K条件下的水头压力产生对涂布厚度影响Table 5 Influence of hydraulic head on coating thickness at different K

表6 不同黏度或涂布速度时,水力压头对涂布厚度的影响Table 6 Influence of hydraulic head on coating thickness at different viscosity and speed
观察表5和表6发现只有在几何参数K=11.11、5.555 即刮刀间隙很大时(H0=1 mm、2 mm)水力压头才会对涂布厚度产生0.017和0.047的增量,其他缝隙小于等于0.5 mm 情况下,黏度μ∈[0.1,10] Pa·s 和涂布速度U*∈[0.005, 0.4] m/s 范围内,水力压头对涂布厚度的影响可以忽略不计。通过改变Fluent软件操作条件增加重力因素的方法也可以模拟水力压头对涂布厚度的影响,得到的结果也演证了式(27)和表5、表6 的结果。由于篇幅所限,不再赘述。分析表明,常用锂电池极片刮刀涂布工况下重力产生的水力压头对涂布厚度的影响可以忽略不计。
3.5 表面张力对逗号刮刀涂布厚度的影响
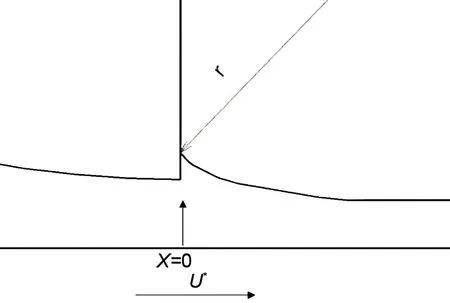
图9 刮刀缝隙出口自由液面形状Fig.9 Free surface after coating gap
在式(14)中,假设压力出口(x=0)处涂布浆料的压力p(0)等于外界大气的压力,即表压p(0)=0,是雷诺润滑方程边界条件的常用设置。在使用Fluent 软件设置边界条件时也可以把出口压力设为0。但在实际涂布工作中,浆料流出压力出口后形成了由液体表面张力、黏性力和液体压力的合力控制自由表面流动。Coyne经过研究得出了涂布自由液面高度h(x)与湿厚度hw之比的关系式h(x)/hw=1+kexp(-λx)[11-12]。如图9所示,在x=+∞处h(x)=hw,p(+∞)=0;在x=0 处p(0)=-σ/r<0。其中,σ 为涂布浆料的表面张力,r 为x=0 处的液面弯曲半径。虽然σ 可以测量,但r 是未知量,所以p(0)也是未知量。因此,能否简单地把p(0)设置为0来应用,需要按不同的条件进行讨论。Kistler 等[14]认为,在刮刀(刚性刮刀和片式刮刀)涂布流场中设置入口和出口压力为零的润滑理论,可以准确地预测涂布厚度和液体压力。Kawabata[15]测量了高黏度浆料(μ=4~6 Pa·s)刮刀流场压力,证实刮刀缝隙出口处压力为0。Sullivan等[16]通过有限元法数值计算和实验证实,刮刀缝隙出口处p(0)的数值与峰值压力相比小至可以忽略不计;在毛细准数不是很大(Ca=μU/σ=3.7和0.9)时,表面张力的影响也可以忽略不计。通常,锂电池极片涂布的黏度在1~10 Pa·s范围,水性负极浆料表面张力0.04~0.05 N/m[3],NMP 浆料体系的表面张力约0.04 N/m(20 ℃)。逗号刮刀涂布速度为0.05~0.2 m/s,由此可以计算出电池浆料的毛细准数Ca>1。毛细准数Ca体现了液体黏性力与表面张力之比,Ca 越大,表面张力对流动的影响也越小。在这种情况下,刮刀缝隙出口处的压力为零的假设成立。在锂电池极片涂布速度较高的工况下,表面张力对涂布厚度的影响可以忽略不计。
4 结 论
本文通过对N-S方程的合理简化,得出刮刀缝隙附近流场的雷诺润滑方程。应用该方程在合理边界条件下求解逗号刮刀涂布流场适用于牛顿流体的力学行为发现,尽管逗号刮刀上游几何尺寸差距明显,但是它的无因次压力-位置曲线几乎重合;涂布湿厚度Hw与刮刀缝隙高度H0的比值在K=R/2H0的取值范围(10~2000)内约等于2/3,而且不受涂布浆料黏度变化和涂布速度变化的影响。通过刮刀涂布理论模型的得出的涂布湿厚度Hw以及压力-位置关系等计算结果与Fluent软件模拟的二维涂布流场的CFD结果高度吻合。
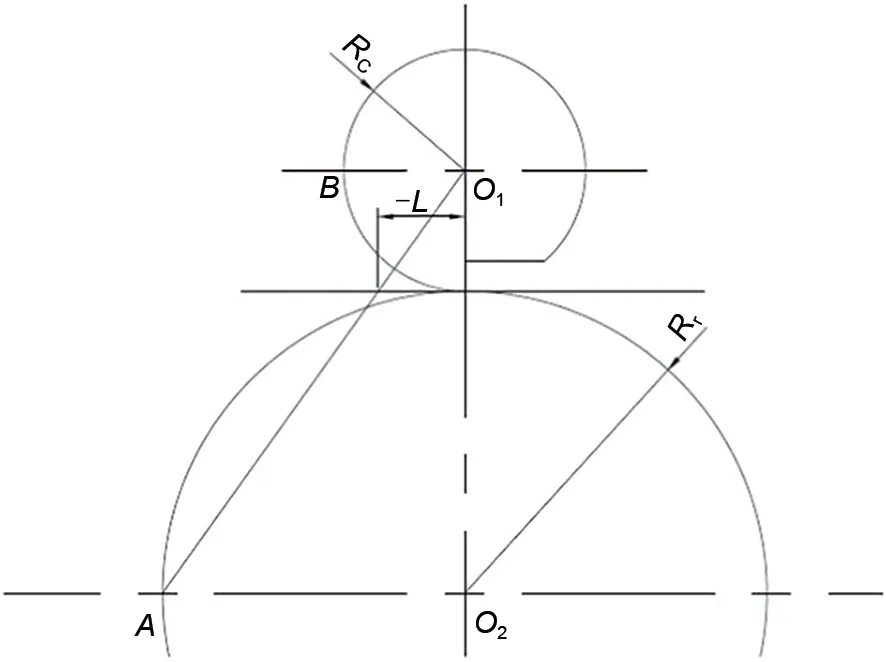
图A1 (-R,0)处于流场中的位置
Fig.A1 Geometrical parameters of comma-roll coating system
