踞数学思想高地,促学科素养提升
2021-03-19李捷生
李捷生


[摘 要] 文章以“简单几何体外接球”为例,借助数学转换思想,通过图形转换、思维转换等方式,培养学生的模式化思维和载体化意识,培养学生的直观想象素养,促进学生实现深度学习,深化学生对知识的理解,提升学生的迁移能力.
[关键词] 数学思想;核心素养;直观想象素养;简单几何体;外接球
引言
数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的[1]. 对此,部分教师在教学中进行了尝试,并取得了一定的成果. 比如培养学生的直观想象素养,朱贤良通过特殊几何体的结构特征来确定外接球球心的位置,梳理了部分规则几何体的解题思路[2];李健通过一节课堂实例,呈现了如何借助一个立体几何问题,提升学生的数学思维品质的具体范例[3];符强如在高三复习中,尝试通过将多面体外接球问题“模式化”,助力学生深度学习[4]. 这些尝试,在解决简单几何体外接球问题的技巧上提供了很好的借鉴方案,也为提升学生的直观想象素养提供了很好的范例.
在这些优秀同行的研究基础上,文章尝试从数学思想统领整个教学过程的角度出发,以“简单几何体外接球”教学为例,谈谈如何在转换思想[5]的引领下,培养学生的模式化思维和载体化意识,为提升学生的数学直观想象素养展示一条实施路径.
教學设计
1. 以圆柱为载体的外接球
教学中,引导学生分别从题4-1、题4-2的几何体棱长和底面垂直的特征中“萃取”线面垂直模型,从题4-3的几何体一个底面与其中一个侧面垂直的特征中“萃取”面面垂直模型,培养学生对知识的概括能力. 通过“问题链”的方式,引导学生寻求这两个特殊模型的解决方案,并通过类比推理,搭建起空间与平面思维的通道,实现思维的转换. 在教学过程中,教师启发学生思考并提出问题:“平面几何中,确定圆心的位置是解决圆的问题的关键,我们是如何确定圆心的?”“找圆心的方法可以类比到找球心的方法吗?”“圆中的弦该类比到球中的哪个几何元素呢?”通过一系列“问题链”的引导,类比新旧知识,进行思维转换的训练,构建获得新知的科学路径,引导学生注重知识之间的联系,渗透转换思想;通过新旧知识的类比,将解决平面几何问题的方法迁移至立体几何问题上,实现从空间到平面的转换,有助于学生对球问题的深度理解. 将条件特殊化后的两个模型的外接球问题(面面垂直、线面垂直)与平面中圆的两条垂直弦的模型进行类比,加深学生对前一次类比的理解. 通过数学思想的引领,提升学生的知识理解能力和迁移能力.
教学思考
1. 由图形转换提升学生的直观想象素养
学生直观想象素养的提升落实到“简单几何体外接球”的教学环节中,教师需要有意识地引导学生认识并理解图形之间的关系,借助图形的特性,将复杂图形的问题转换为简单图形的问题,将陌生的图形转换为熟悉的图形,帮助学生进行深度理解,培养学生的模式化思维和载体化意识.
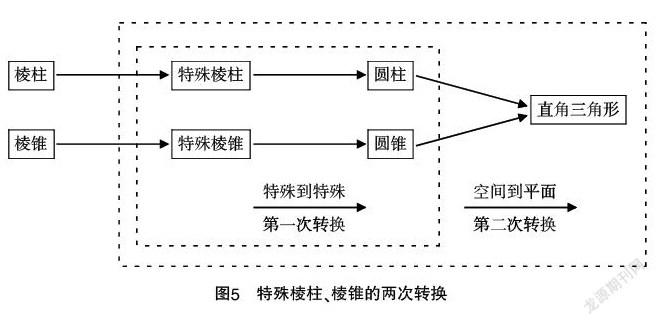
在“以圆柱、圆锥为载体的外接球”的教学中,整个教学围绕“如何进行转换”展开,目的是让学生充分体会两次转换(见图5)的意义,引导学生借助图形的对称性及图形之间的转换,实现将特殊棱柱、棱锥问题转换为圆柱、圆锥问题,提升直观想象素养.
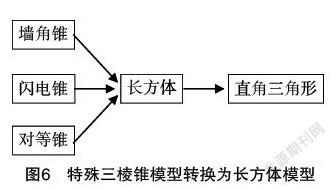
在“以长方体为载体的外接球”的教学中,以转换思想引领学生观察特殊三棱锥的特性,联想到长方体的棱垂直多、对角线相等的几何特性,将特殊三棱锥还原为长方体,实现特殊三棱锥模型与长方体模型的转换(见图6). 一方面,教师应该培养学生关注几何体特殊性质的习惯,培养学生能从一般几何体中“萃取”某一类特殊几何体的能力,并能用直观形象的名称表达出有类别的特殊性质,这实际上就是学生直观想象素养在“能用数学的眼光看世界”“能用数学的语言表达世界”的一种具体表现形式. 另一方面,教师不仅要引导学生从多个视角去看待同一个几何体,而且还要引导学生用联系的眼光去看待多个几何体,从几何体之间的联系这个角度去直观感知几何体,掌握研究几何图形的基本方法,提升直观想象的素养[6].
2. 由思维转换提升学生的直观想象素养
史宁中认为:“几何教学,更好的教学过程应当是先讨论二维空间的情况,然后类比到三维空间的情况,最后抽象出一般n维空间.”[7]球作为圆在三维空间中的拓展,是提升学生直观想象素养很好的一个素材. 但是,由于学生原有的几何储备知识大部分属于二维平面知识,因此在实际的教学中,教师需要引导学生进行思维转换,将三维空间问题降维到他们熟悉的二维平面问题,然后调用二维平面中相应的知识进行类比并解决三维空间问题.
上述教学设计,目的是引导学生站在思想高度去看问题,培养学生高观点下思考问题的能力,通过图形转换和思维转换将简单几何体分别转化为圆柱模型、圆锥模型、长方体模型、垂直模型等四种模型,让学生参与并经历这些转化过程,促使学生更加关注图形特征、图形之间的联系,从而提升学生的直观想象素养. 另一方面,通过数学思想的引领,让学生感悟从整体的视角关注知识之间的联系,感悟从模型的视角去整合知识,有利于促进学生进行深度学习,深化学生对知识的理解,培养学生的模式化思维和载体化意识,提升学生的迁移能力.
结束语
张奠宙教授指出:“每一门数学学科都有其特有的数学思想,赖以进行研究(或学习)的导向,以便掌握其精神实质. 只有把数学思想掌握了,计算才能发生作用,形式演绎体系才有灵魂.”素养的培养不可能一蹴而就,学生从理解到感悟需要一个过程,需要教师进行有意识的引导. 因此,教学活动需要数学思想作为引领,借助具体的知识作为载体,提升学生的数学核心素养,培养学生的知识理解、迁移、应用的能力.
参考文献:
[1] 中华人民共和国教育部制定.普通高中数学课程标准(2017年版)[S]. 北京:人民教育出版社,2018.
[2] 朱贤良. 众里寻“心”千百度 繁华落尽识真颜——确定多面体外接球球心位置的一般途径与四个特殊模型[J]. 中学数学研究(华南师范大学版),2019(21).
[3] 李健. 直观把握数学本质动态提升思维品质——从教材中一个立体几何问题例谈变式教学[J]. 数学通报,2019(10).
[4] 符强如. 巧建数学模型 助力深度学习——以模式化思想求解多面体外接球问题为例[J]. 高中数学教与学,2019(17).
[5] 吴炯圻,林培榕. 数学思想方法:创新与应用能力的培养[M]. 厦门:厦门大学出版社,2009.
[6] 宋建辉. 基于学科核心素养的2019高考全国卷立体试题分析[J]. 数学通报,2020(01).
[7] 史宁中. 数学思想概论(第4辑)——数学中的归纳推理[M]. 长春:东北师范大学出版社,2010.
2711501186206
