“必要探路”中的“路”从何而“探”

黄昌毅

[摘  要] “必要探路”是破解含参函数不等式恒成立问题的重要策略. 将函数不等式问题转化为两函数图像的位置关系，通过观察函数图像，直观得到临界状态，是寻找必要条件的关键步骤.

[关键词] 必要探路;恒成立问题;直观想象

函数不等式恒成立问题是高考考查的热点、难点. 为寻找解决这类问题的突破口，往往需要先利用必要条件探路（通过取自變量一特殊值使不等式恒成立），得到参数的取值范围，随后验证其充分性，这就是“必要探路”解题的思想方法. 因此，如何合理正确地得出必要条件是解决这类问题的关键，那么这个必要条件（特殊值）该选取谁？选取的依据是什么？

下面笔者以2020年两道高考试题为例，探索“必要探路”中的“路”从何而“探”.

题1 （2020年高考山东卷第21题）已知函数f（x）=aex-1-lnx+lna.

（1）当a=e时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积;

（2）若f（x）≥1，求a的取值范围.

分析：（1）略;

（2）f（1）≥1，得a+lna≥1. 设φ（a）=a+lna，易知φ（a）=a+lna单调递增，又φ（a）=a+lna≥1=φ（1），可得a≥1.

下面证明a≥1满足条件：f（x）=aex-1-lnx+lna≥ex-1-lnx. 易证lnx≤x-1，即x≤ex-1，当且仅当x=1时取等号，则ex-1-lnx≥x-（x-1）=1，当且仅当x=1时取等号. 综上，a≥1.

这种解法简洁直观，让教师和学生眼前一亮，但在惊讶感叹后，却带来了很大的疑惑：“为什么取x=1呢？为什么不取x=2呢？”有些人说“只有取x=1时，得到的a的取值范围较简洁”，看似有道理，但数学逻辑上却缺乏严谨性，所以关键还是要探究“为什么要取x=1”.

因为函数y=f（x）的解析式中包含ex，lnx，而y=ex与y=lnx互为反函数，即图像关于直线y=x对称，所以是否能从图像对称的角度去探究呢？

探究：f（x）=aex-1-lnx+lna≥1⇔·ex≥ln

·x，易知y=·ex与y=ln

·x互为反函数，即图像关于直线y=x对称，则·ex≥ln

·x⇔·ex≥x≥ln

·x. 转化为ex-1≥x恒成立，即y=ex-1的图像恒在y=x的上方. 由图1可知，≤1，即a≥1. 当y=ex-1与y=x相切于点（1，1）时a=1，即a≥1取等号的条件为x=1.

此时豁然开朗，原来x=1不是随便取的，y=·ex，y=ln

·x同时与y=x相切时，如图2所示，切点的横坐标即为x=1，所以x=1为临界值.

题2 （2020年高考全国Ⅰ卷理科第21题）已知函数f（x）=ex+ax2-x.

（1）当a=1时，讨论f（x）的单调性;

（2）当x≥0时，f（x）≥x3+1，求实数a的取值范围.

分析：（1）略;

（2）ex+ax2-x≥x3+1，即ex-x3+ax2-x-1≥0. 设g（x）=ex-x3+ax2-x-1，依题意得g（2）≥0，解得a≥.

下面证明a≥满足条件：g（x）=ex-x3+ax2-x-1≥ex-x3+x2-x-1，即证明ex-x3+x2-x-1≥0，即证明

x3+x2+x+1

e-x≤1.

设h（x）=

x3+x2+x+1

e-x，则h′（x）=-x（x-2）

x+

e-x. 易求得y=h（x）在

0，

，（2，+∞）递减，在

，2

递增，则hmax（x）=max{h（0），h（2）}=1，即h（x）≤1.

这题取x=2就更让人感到困惑了，那么x=2从何得来的呢？

探究：①当x=0时，上述不等式显然成立，符合题意，此时a的取值范围为一切实数;

②当x>0时，可得ex+ax2-x≥x3+1⇔≥x-a，即y=的图像恒在y=x-a的上方.

设φ（x）=，对其求导，得φ′（x）==

ex+1

.

设m（x）=ex+1，对其求导，得m′（x）=ex>0，则m（x）>m（0）=0.

所以φ′（x）>0，所以φ（x）在（0，+∞）上单调递增.

设y=与y=x-a的切点为P（x，y），则φ′（x）=，代入化简得（x-2）

e-x-x-1

=0，易证明e-x-x-1>0，所以x=2，此时a=.

如图3所示，即y=与y=x-a相切时，切点的横坐标为x=2. 故先取特殊值x=2. 当然也可以这样转化：ex+ax2-x≥x3+1⇔≥-ax+1，如图4所示，当y=与y=-ax+1相切时，切点的横坐标为x=2.

“必要探路”解题方法中由必要条件得到的范围是必须满足的范围，而如果同时又证明了这个范围内所有的数都可以取到，那么这个过程在逻辑上就是严密的，这体现了数学的逻辑推理素养;而寻找这个“必要条件”，则体现了数学的直观想象素养. 史宁中教授说：“数学知识的形成依赖于直观，数学知识的确定依赖于推理，也就是说，在大多数情况下，数学的结果是看出来的而不是证出来的.”[1]将函数不等式恒成立问题转化为两函数图像的位置关系，通过观察函数图像，直观得到临界状态，虽然严谨性不足，但却能提供解题方向.

历年高考对函数恒成立问题的考查频繁，其中有不少试题均可使用“必要探路”解题方法破解，例如：

题3 （2019年高考全国Ⅰ卷文科第20题）已知函数f（x）=2sinx-xcosx-x，f′（x）为f（x）的导数.

（1）证明：f′（x）在区间（0，π）存在唯一零点;

（2）若x∈[0，π]时，f（x）≥ax，求a的取值范围.

分析：（1）略;

（2）依题意，f（π）≥aπ，解得a≤0.

下面证明a≤0满足条件：

由（1）知，f′（x）在（0，π）只有一个零点，设为x，且当x∈（0，x）时，f′（x）>0;当x∈（x，π）时，f′（x）<0. 所以f（x）在（0，x）上单调递增，在（x，π）上单调递减. 又f（0）=0，f（π）=0，所以，當x∈[0，π]时，f（x）≥0≥ax.

因此，a的取值范围是（-∞，0].

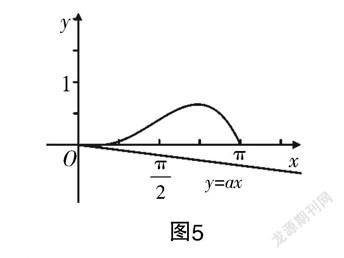
探究：f（x）≥ax，即x∈[0，π]时，y=f（x）的图像始终在y=ax的上方. 由（1）可大致作出函数y=f（x）的图像，如图5所示，由图可知a≤0.

题4 （2012年高考新课标卷文科第21题）设函数f（x）=ex-ax-2.

（1）求f（x）的单调区间;

（2）若a=1，k为整数，且当x>0时，（x-k）f′（x）+x+1>0，求k的最大值.

分析：（1）略;

（2）（x-k）f′（x）+x+1=（x-k）（ex-1）+x+1>0. 取x=1，代入得k<1+;取x=2，代入得k<2+，即k≤2.

下面证明k=2满足条件，即证（x-2）ex+3>0成立，下略.

探究：（x-k）（ex-1）+x+1>0⇔> -x+k.

即当x>0时，y=的图像始终在y=-x+k的上方.

令g（x）=，则g′（x）=<0.

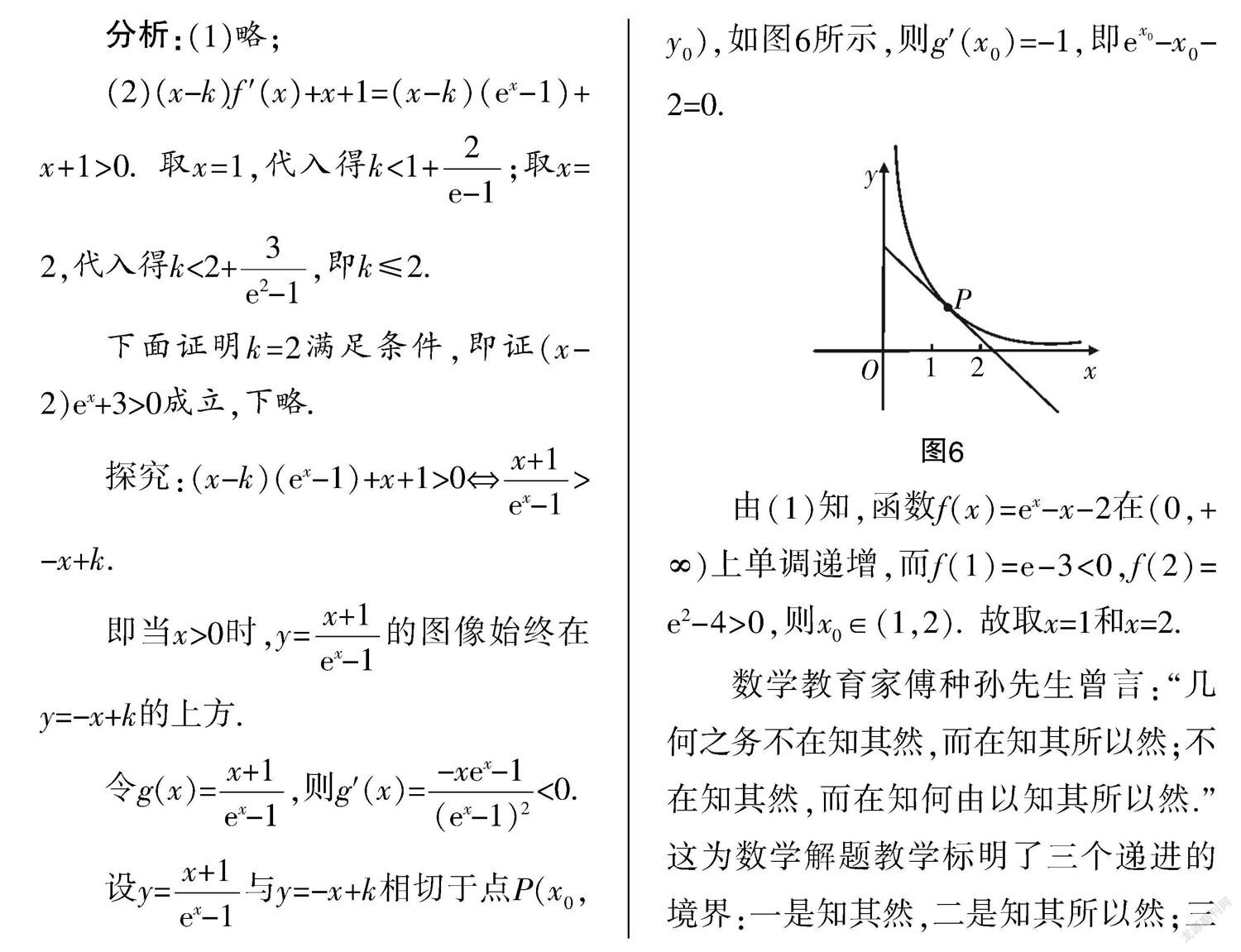
设y=与y=-x+k相切于点P（x，y），如图6所示，则g′（x）=-1，即e-x-2=0.

由（1）知，函数f（x）=ex-x-2在（0，+∞）上单调递增，而f（1）=e-3<0，f（2）=e2-4>0，则x∈（1，2）. 故取x=1和x=2.

数学教育家傅种孙先生曾言：“几何之务不在知其然，而在知其所以然;不在知其然，而在知何由以知其所以然.”这为数学解题教学标明了三个递进的境界：一是知其然，二是知其所以然;三是知何由以知其所以然[2]. 这告诉我们，在平常的解题教学中，我们除了传道、授业以外，解惑也是一个非常重要的环节，将问题分析清楚，厘清解答背后的数学思维，把握数学问题的本质，教会学生用数学思维思考问题、解决问题，这才是教学的最终目标.

参考文献：

[1]  盛国平. 让数学抽象在概念教学中落地生根——以“函数的奇偶性”为例[J]. 中学数学教学参考，2019（18）.

[2]  牟庆生. 知其然、知其所以然、知何由以知其所以然——由2016年浙江理第19题引发的数学解题教学的思考[J]. 中学数学，2016（23）.

3129500589290