异面直线所成角问题的解法探究

盛锦星

[摘  要] 异面直线所成角问题的难度中等，求角方法较为多样，可直接通过平移变换将异面直线转换到同一平面，也可依托空间向量法来求解. 文章深入探究异面直线所成角问题的解法，并反思总结，提出几点建议.

[关键词] 异面直线;角度;平移法;空间向量

异面直线所成角问题是立体几何常见问题类型，解题核心是构建异面直线所成的平面角，常用的方法也较为丰富，下面深入探究.

[⇩] 引例探究

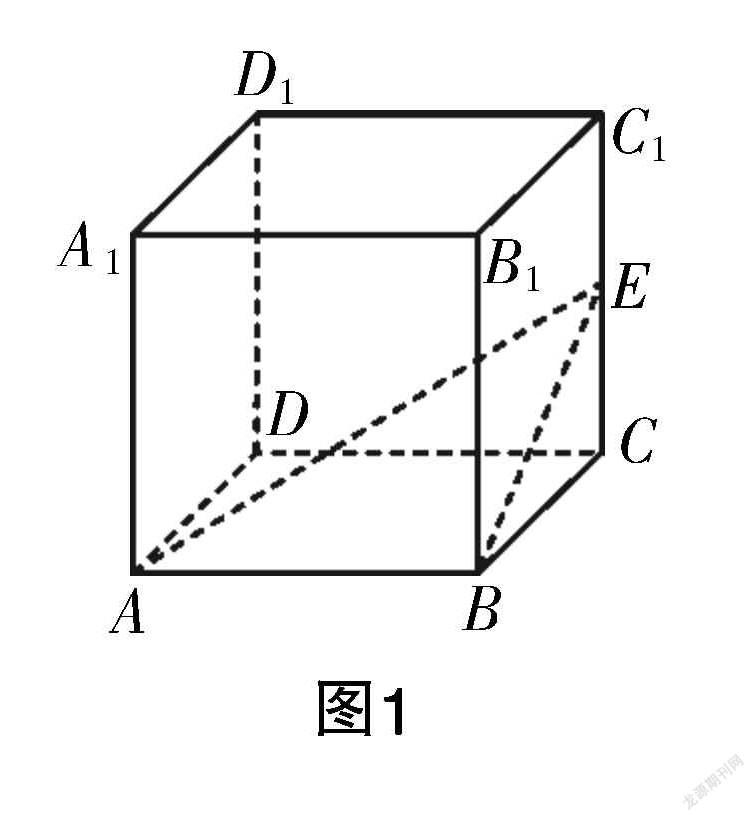
例题：在正方体ABCD-ABCD中，已知点E是CC的中点，则异面直线AE和CD所成角的正切值为________.

分析：充分利用正方体的特性，可得CD∥AB，通过平行或平移将异面直线问题转化为共面直线AB与AE之间的问题. 要求两者所成角的正切值，将其放置在△ABE中进行.

详解：在正方体ABCD-ABCD中，可知CD∥AB，所以异面直线所成的角为∠EAB，如图1所示. 可设正方体的边长为2a，点E是CC的中点，则CE=a，进一步可求得BE=a. 在Rt△EAB中，有tan∠EAB===，即异面直线AE和CD所成角的正切值为.

[⇩] 方法总结

上述是一道异面直线考题，主要考查异面直线所成角的相关知识，对学生的空间想象和运算能力要求较高. 上述采用了求异面直线问题常用的平移法，掌握方法的解题策略十分重要. 平移法求异面直线所成角的基本思想是平移转换，核心内容是直线平移或探寻平行直线，以及依托三角形构造夹角，一般分三步进行，过程总结如下.

第一步，对异面直线进行平移或平行转换，有两种策略：一是固定一条直线，平移另一条;二是将两条直线同时平移到某一特殊位置，构成同一平面.

第二步，构建异面直线所成角，或者证明图形中某一夹角为所求角.

第三步，依托所求角构造三角形，通过解三角形完成求解.

另外，对于异面直线所成角问题，需要关注角度的取值范围，即取值范围为

0，

，故完成角度求解后，还需对其验证.

[⇩] 强化拓展

实际上可将平移法细分为三种，分别为中位线平移、直接平移、补形平移，上述引例的平移过程可视为直接平移，下面结合实例进一步探究其他两种平移.

1. 平移破异面——中位线平移

中位线平移，即把握图形的中位线，利用中位线的平行特性完成平移，解题时需要关注图形中的中点，依托中点构造中位线.

例1 已知点A和B在以PC为直径的球O的表面上，并且AB⊥BC，AB=2，BC=4. 若球O的表面积为24π，则异面直线PB和AC所成角的余弦值为________.

分析：本题目较为特殊，依托球考查异面直线所成角、球体的相关计算. 可作出图，取线段的中点，利用中位线性质来实现异面直线平移. 将异面直线放置在三角形中，利用余弦定理得到所求角的余弦值.

详解：设球O的半径为R，球的表面积为24π，则半径R=.

根据题意构图，分别取PA，AB，BC的中点M，N，E，连接MN，ME，NE，AE，如图2所示.

分析可知，PC=2R=2，PA⊥平面ABC. 因为AB⊥BC，由勾股定理可得AC==2，PA=2，PB=2. 因为点M和N分别为PA和AB的中点，由中位线性质可知MN∥PB，并且MN=PB=. 同理可得NE∥AC，且NE=AC=. 进一步可推得AE=2，ME=3.

因为MN∥PB，NE∥AC，所以异面直线PB和AC所成角为∠MNE或其补角. △MNE中，已知MN=，ME=3，NE=，由余弦定理可得cos∠MNE==-，所以异面直线PB和AC所成角的余弦值为.

2. 平移破异面——补形平移

补形平移法的核心是“补形”，即通过补充图形来实现平移转换，其中“补形”的目标是为了后续的平移相交，“补形”时要注意依托图形固有特征，顺势生成.

例2 如图3所示，在正方体ABCD-ABCD中，已知点M为AB的中点，点N为DD的中点，则异面直线BM与CN所成角的大小为________.

分析：本题目同样依托正方体构建异面直线，在原有正方体内难以直接构建平行直接完成平移，可在正方体的右侧“补”一个正方体，再进行平移相交转换，后续通过解三角形来求角度.

详解：如图4所示，在正方体的右侧“补”一个边长相等的正方体. 取CE的中点为P，由于点M为AB的中点，连接CP，则有CP∥BM，则∠NCP或其补角为异面直线BM与CN所成的平面角.

再連接NP，设正方体的边长为a，可求得CN=CP=a. 由勾股定理可得NP=a. 由于△NCP的三边满足关系CN2+CP2=NP2，所以∠NCP=90°，即异面直线BM与CN所成角的大小为90°.

[⇩] 解法另探

上述深入探究了求异面直线所成角问题的平移法，从建模角度来看，还可采用空间向量法来求解. 下面解读方法原理，并结合实例探究.

空间向量法，即依托所求图形构建空间坐标系，分别求出异面直线的向量坐标，然后利用向量之间的角度关系来求解，基本原理如下：设直线l，m方向的向量分别为a和b，则两直线所成角θ的余弦值为cosθ=.

例3 如图5所示，已知四边形BCCB为正方形，且AB=BC=2，平面BCCB⊥平面ABC，∠ABC=120°，则异面直线BC与AC所成角的余弦值为________.

解析：本题直接构建了两个相交平面，求异面直线所成角的大小，可以使用空间向量法.

可以点B为坐标原点，BC为y轴，BB为z轴，在平面ABC中，作x轴⊥y轴，建立图6所示的空间直角坐标系.

由题意知∠ABC=120°，AB=BC=2，所以点A（，-1，0），点B（0，0，0），点C（0，2，0），C（0，2，2）. 所以向量=（-，3，0），=（0，2，2），则异面直线BC与AC所成角的余弦值cos〈，〉==.

评析：上述在求异面直线所成角的余弦值时采用了空间向量法，该方法通常分三步进行：第一步是建坐标系，求关键点坐标;第二步，求所涉异面直线的向量坐标;第三步，利用定理求夹角的余弦值. 从解题过程来看，空间向量法的程序性更强，思维难度较低，只需根据方法流程求解即可.

[⇩] 总结思考

上述充分探究了求异面直线所成角的两种解法，平移法是基于平移变换所构建，空间向量法更侧重几何体系的构建，程序性更强，两种解法各具特色，实际解题时可根据问题情景灵活选取.

异面直线所成角的解法探究教学中，建议关注以下几点：

关注解法本质，理解方法原理. 开展解法探究，要立足方法本质，让学生充分掌握方法原理，如平移法的知识本质就是平行线的性质，通过平移来实现线段代换.

关注方法的构建思路，应重点教学方法的使用过程，引导学生合理使用，严谨论证，如空间向量法分三步进行解题构建，每一步环环相扣.

倡导方法拓展，提升学生思维的灵活性. 上述仅列举了该类问题的两种常用方法，但不局限于此. 教学中要注重培养学生的思维，合理拓展解法，可利用“一题多解”进行解法探究，促进学生的思维发展.

3254500589276