截止波导管在腔体屏蔽中的应用研究
2021-03-18刘志坚涂志章罗灵琳陈潇雅王畅
刘志坚,涂志章,罗灵琳,陈潇雅,王畅
截止波导管在腔体屏蔽中的应用研究
刘志坚1,涂志章1,罗灵琳1,陈潇雅2,王畅1
(1. 昆明理工大学 电力工程学院,云南 昆明 650500;2. 安徽金寨抽水蓄能有限公司,安徽 六安 237300)
依据波导管的高通滤波性能,设计了一种带有波导管结构的金属屏蔽腔体。采用HFSS有限元仿真软件,分别仿真了矩形孔和加了一段矩形波导管的腔体模型,分析了在1.0~2.0 GHz频率范围内屏蔽效能和电磁场强度变化。并进一步研究了平面波不同极化方向以及波导管长度对腔体屏蔽效能的影响,得出0沿轴(沿短边)极化整体屏蔽效能最好,波导管长度与腔体屏蔽效呈正相关。研究结果表明,加装波导管能够提高带孔腔体的屏蔽效能,在波导长度为6 mm时,金属腔体截止频率从原有1.16 GHz提高至1.5 GHz,并且腔体谐振频率明显减小、谐振次数也相对减少。
波导管;屏蔽效能;截止频率;腔体谐振
0 引言
现如今,电气产品种类繁多,已经深入到人们生活的各个领域。这些电气产品改善了日常生活,同时也带来了大量的电磁污染。机箱电磁屏蔽是一种非常直观且有效地防止电磁辐射的方法,在机箱设计过程中为散热、通风、连接线端口等设置的孔缝是机箱电磁屏蔽效能降低的主要原因[1-2]。通过对腔体屏蔽效能研究,一方面能够对不同设备采取最合理的屏蔽措施;另一方面能够尽早发现问题,缩短研发周期,节省人力物力[3]。
目前,腔体屏蔽特性研究多以开孔的矩形屏蔽空腔为研究模型,通常采用实验测试、数值仿真和解析分析3种方法[4]。相对于实验分析的局限性、离散性等缺陷,数值分析方法能灵活有效地反映腔体随外界磁场环境变化后屏蔽效能的变化趋势,从而能够更好地为各类型屏蔽腔体屏蔽性能顶层设计提供理论与技术支撑[5-6]。Robinson基于波导理论和等效电路原理推导出计算带孔腔体谐振频率和宽频带屏蔽效能的等效电路算法[7]。文献[8]利用TLM数值方法研究孔缝腔体分别在近场和远场情况下,影响SE的关键因素并对实际机箱屏蔽特性进行研究。文献[9]研究了频率、孔径以及孔阵列对泡沫铝材料屏蔽效能的影响。
本文基于Robinson数值方法将孔缝腔体模型等效的原理,通过HFSS建模,在小孔上增设一节波导管,利用波导管的高通滤波特点,对射入波导管内的电磁能量进行反射、吸收损耗,从而达到提升屏蔽效能的作用。
1 开孔腔体数值模型分析
1.1 屏蔽效能定义
屏蔽性能的衡量标准是屏蔽效能(shielding effectiveness,SE):在电磁干扰源下,屏蔽体安放前后电场强度或磁场强度的比值[10]。
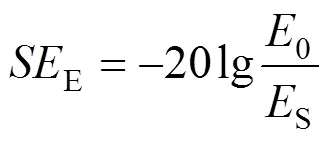
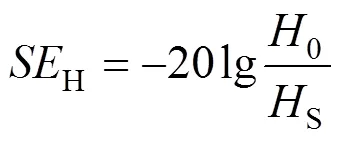
1.2 Robinson方法
该方法的总体思想是将带矩形孔的腔体等效为终端短路的波导,将孔等效为左右两端短路的共面带状传输线,利用等效电路的原理解决电磁场耦合问题[11-12],如图1所示。
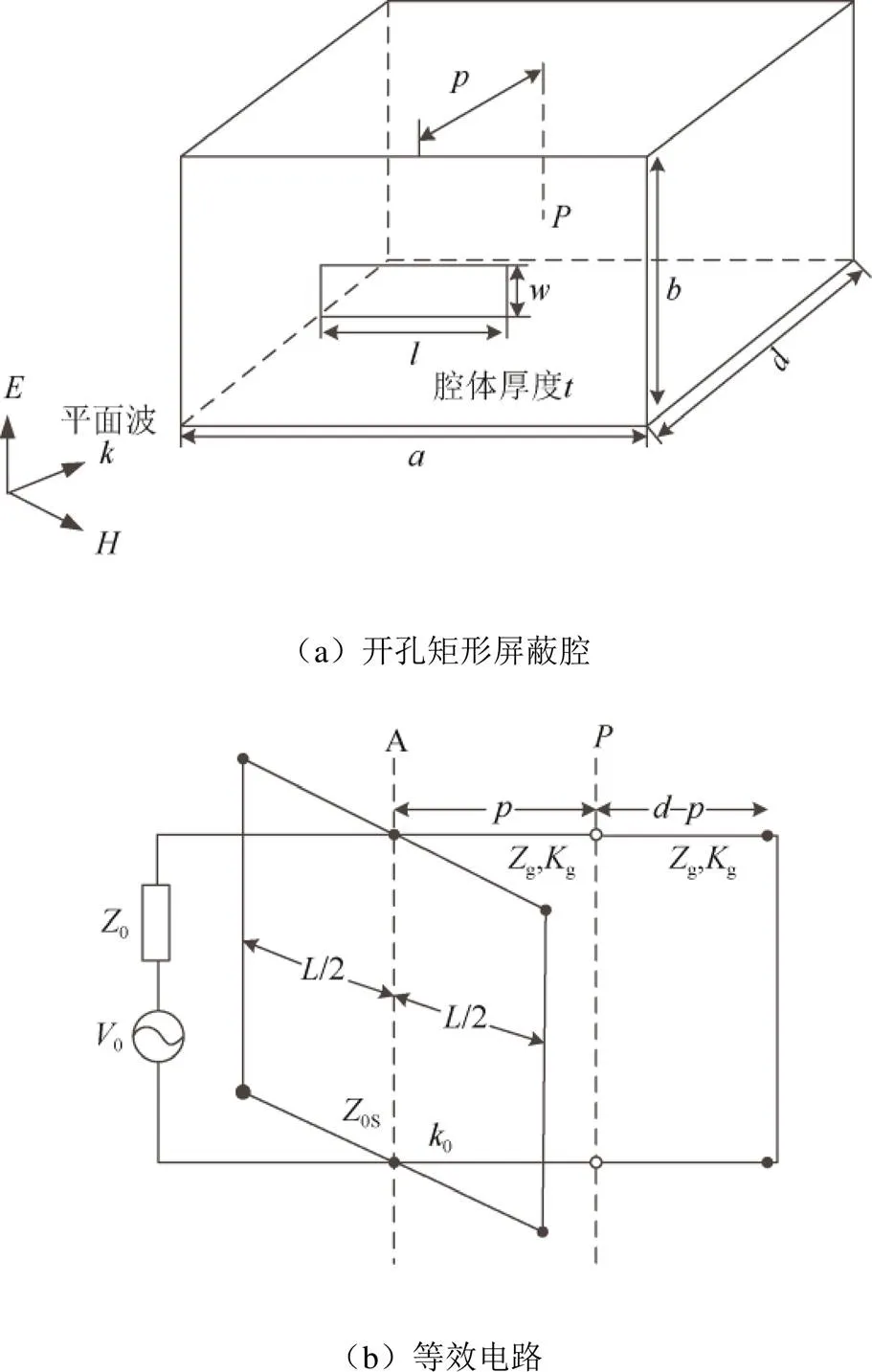
图1 等效电路研究模型
如图1所示,激励被等效成电压源0,自由空间波阻抗≈377 Ω。传播系数和特征阻抗分别为g和g,自由空间波数为0=2π/,矩形开孔被等效为两端短路的共面带状传输线[12-14],根据Gupta理论,其特征阻抗为:
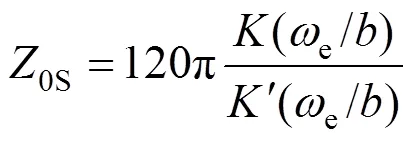
式中:e为孔的等效宽度;和′为椭圆积分,即:

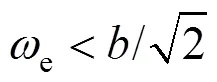
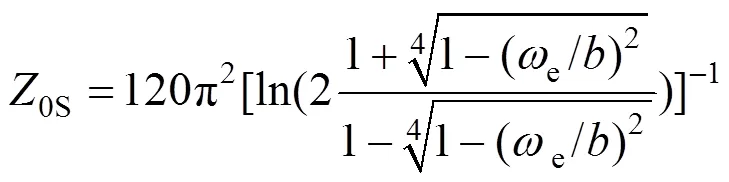
通过对矩形孔终端阻抗进行/2变化至中心位置,结合孔与腔体耦合系数,得孔的等效阻抗为:
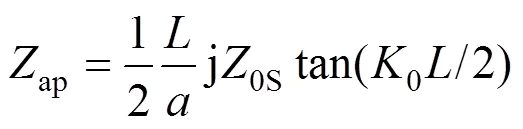
根据戴维南定理,可得矩形孔处的等效电压1=0ap/(0+ap)以及等效阻抗1=0ap/(0+ap)。根据特性阻抗和传播系数g,g,可得观测点处的等效电压、源阻抗以及负载阻抗分别为:
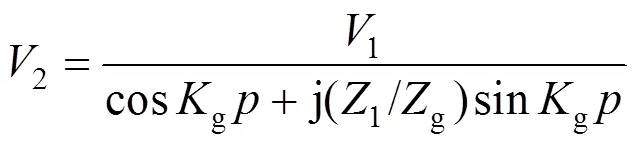
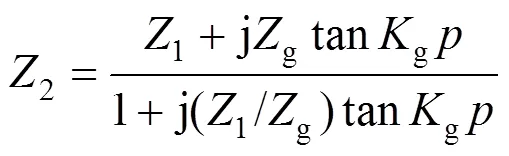
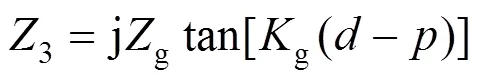

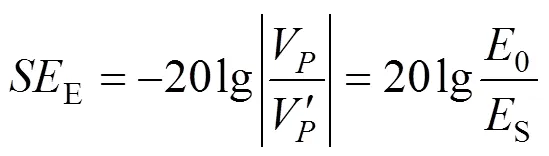
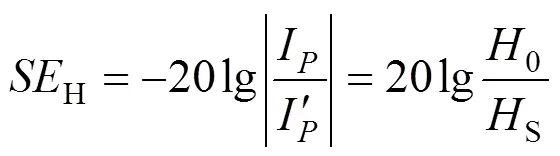
式中:0和S分别为屏蔽前后的电场强度;0和S分别为屏蔽前后的磁场强度。
2 截止波导管的屏蔽效能
当电磁波通过波导管时,截止波导管利用其高通滤波的特性,使电磁波频率在波导截止频率以下时被截止或者衰减,通常要求其长度要比横截面积直径或最大线性尺寸至少大3倍[15]。金属波导管的最低截止频率c只与波导管横截面积内尺寸有关[15-16],其中矩形波导管最低截止频率为:
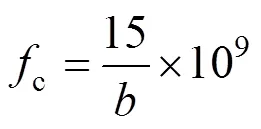
式中:表示矩形波导管横截内直径,cm。对应为:
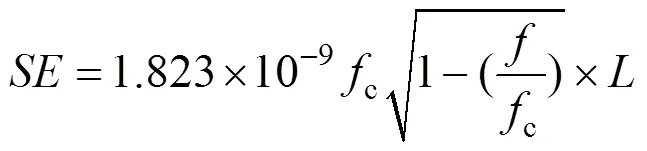
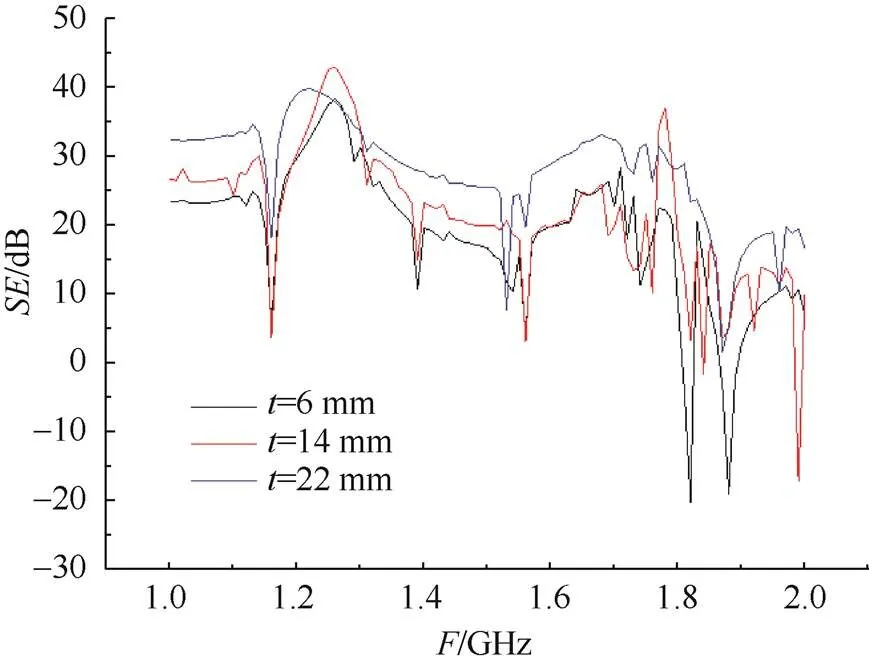
当< 通常在设计截止波导管时,以干扰源max确定波导管c的值,应使< 带孔屏蔽腔体的几何模型如图2所示。屏蔽腔体尺寸为462 mm×212 mm×488 mm,壁厚2 mm,材料为铝,激励设置为平面波,开孔位于前侧中心,矩形孔尺寸90 mm×10 mm,孔辐射边界尺寸为800 mm×500 mm×850 mm。场强监测点位于腔体中心,电场强度为1 V/m,求解频率为1.5 Hz,扫描频率设置1.0~2.0 GHz,求解步长设置10 MHz。 图2 矩形波导孔腔体三维模型 在腔体正面开设一小孔,分别对加/不加波导管两种情况进行讨论,0沿轴方向,波导管厚度=1 mm,长度=6 mm。 由图3(a)可知,加装矩形波导管腔体的屏蔽效能明显高于矩形孔腔体。在1.0~2.0 GHz整段频率范围下,加装矩形波导管的曲线基本位于矩形孔曲线的正上方。 图3 腔体中心SE/电磁场强度图 由电磁场曲线图3可知,加装矩形波导管后腔体监测点电磁场强度要更低。因为波导管具有高通滤波性,能使电磁波频率在波导截止频率以下时被衰减,在1.5 GHz之前,几乎没有电磁波能量进入矩形波导管腔体中(监测点处电磁场强度几乎均为0)。但是,矩形孔腔体在1.16 GHz时发生腔体谐振,监测点电场强度急剧增大,屏蔽效能值也低于–15 dB。 加装矩形波导管的腔体在频段1.0~2.0 GHz内,腔体谐振次数明显较少。同时,也可以看到两者所发生谐振频率点是基本一致的,这是因为腔体谐振是由腔体本身尺寸决定,与是否加入波导管无关。 从图4中可以看到,在频率1.16 GHz时矩形波导管腔体内部发生明显谐振,电磁波能量通过小孔耦合进入腔体内部。而加装矩形波导管的腔体内部电磁波能量明显较弱,大多集中在腔体外部。 图4 1.16 GHz下XY平面电场强度分布图 通过矩形孔与波导矩形孔腔体对比仿真研究,验证了加装波导管能够提高带孔腔体的屏蔽效能,为下面分析波导矩形孔腔体屏蔽效能影响因素做铺垫。 为了进一步验证平面波不同极化方向对屏蔽效能的影响,采取3种平面波极化方向:0沿轴方向;0沿轴方向;0沿45°方向,其它条件不变,仿真分析如图5所示。 图5 不同极化方向下SE图 由图5可以看出,矩形波导在1.7 GHz前,0沿轴(沿短边)极化的绝大部分屏蔽效能值是高于0沿轴(沿长边)和45°方向极化,说明在1.0~1.7 GHz时,平面波0沿轴极化通过小孔耦合进入机箱内部的能量最少。在1.7~2.0 GHz内,0沿轴极化的屏蔽效能相对较好。相比较而言,当0沿45°方向极化时,电磁波能量(相当于沿着矩形孔斜边进入)最容易进入腔体内部。因此,电磁波能量沿着长边方向最容易进入腔体内部,极化方向可作为设计矩形孔尺寸的依据。 为了研究波导管长度对屏蔽效能的影响,选择6 mm,14 mm,22 mm 3种不同长度矩形波导管。0极化方向默认沿轴,其它条件不变,仿真分析如下: 由图6可知,当波导管从6 mm增长至22 mm时,整体上看是波导管越长腔体屏蔽效能越好。但考虑到腔体开孔主要是为了散热,波导管长度过长会影响腔体的散热效果。所以在设计波导管长度时,应考虑设备所需的屏蔽效能等级,在不影响散热效果情况下适当增加波导管长度。 图6 不同矩形波导长度下SE图 通过上述研究表明,加装波导管的腔体屏蔽效能明显优于矩形孔腔体,随着波导管长度增加屏蔽效果也逐渐变好。但是,由于腔体开设小孔要考虑散热效果,因此波导管的长度应在不影响散热前提下适当增加。因为矩形波导管滤波性,波导矩形孔腔体相比于矩形孔腔体的截止频率c有所提高,腔体谐振强度也在一定程度上被削弱,在性能上优于矩形孔腔体。 [1] 路宏敏, 余志勇, 李万玉. 工程电磁兼容[M]. 西安: 西安电子科技大学出版社, 2010. LU HONGMIN, YU ZHIYONG, LI WANYU. Engineering electromagnetic compatibility[M]. Xi’an: Xidian University Press, 2010(in Chinese). [2] 李杰, 杨志华, 王应芬, 等. 基于孔缝箱体屏蔽效能的研究[J]. 电力科学与工程, 2020, 36(5): 69-74. LI JIE, YANG ZHIHUA, WANG YINGFEN, et al. Research on shielding effectiveness of box with aperture[J]. Electric Power Science and Engineering, 2020, 36(5): 69-74(in Chinese). [3] 陈岳承, 刘树中, 傅庆丰. 孔缝对金属机箱的屏蔽效能影响分析[J]. 电子世界, 2019(11): 24-26. CHEN YUECHENG, LIU SHUZHONG, FU QINGFENG. Analysis of influence of apertures on shielding effectiveness of metal chassis[J]. Electronics World, 2019(11): 24-26(in Chinese). [4] 郝建红, 公延飞, 蒋璐行, 等. 开有介质封堵环状孔缝的双金属腔体屏蔽效能的解析研究[J]. 电工技术学报, 2018, 33(1): 131-139. HAO JIANHONG, GONG YANFEI, JINAG LUXING, et al. Analytical formulation for the shielding effectiveness of a cascaded double metallic enclosures with an annular aperture sealed by conductive material[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 131-139(in Chinese). [5] 罗名祺, 金华标, 王卓, 等. 船用屏蔽箱体孔腔耦合谐振的仿真分析[J]. 舰船科学技术, 2018, 40(11): 124-127. LUO MINGQI, JIN HUABIAO, WANG ZHUO, et al. Simulation analysis of cavity coupling resonance in marine shielded box[J]. Ship Science and Technology, 2018, 40(11): 124-127(in Chinese). [6] 高雪莲, 马士杰, 杨凯, 等. 考虑高次模的孔缝腔体屏蔽效能计算方法[J]. 高电压技术, 2017, 43(10): 3344-3350. GAO XUELIAN, MA SHIJIE, YANG KAI, et al. Method for shielding effectiveness of enclosure with apertures including high-order mode[J]. High Voltage Engineering, 2017, 43(10): 3344-3350(in Chinese). [7] REN DAN, DU PING’AN, HE YIN, et al. A fast calculation approach for the shielding effectiveness of an enclosure with numerous small apertures[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(4): 1033-1041. [8] 吴贤. 电子设备机箱的电磁屏蔽特性研究[D]. 成都: 电子科技大学, 2011. WU XIAN. Research on electromagnetic shielding characteristics of enclosures of electronic equipment[D]. Chengdu: University of Electronic Science and Technology of China, 2011(in Chinese). [9] 王录才, 张淑凯, 王艳丽, 等. 基于CST泡沫铝通风窗屏蔽性能的有限元模拟[J]. 新技术新工艺, 2015(3): 59-63. WANG LUCAI, ZHANG SHUKAI, WANG YANLI, et al. Simulation of ventilation window shielding performance of aluminum foam based on CST[J]. New Technology & New Process, 2015(3): 59-63(in Chinese). [10] 刘洪, 尹力, 蔡科, 等. 基于有限元方法的探针台屏蔽箱屏蔽效能分析[J]. 计算机仿真, 2018, 35(9): 229-232. LIU HONG, YIN LI, CAI KE, et al. Shielding effectiveness analysis of shielding enclosure for prober system based on FEM[J]. Computer Simulation, 2018, 35(9): 229-232(in Chinese). [11] 曹张帅, 刘强, 闫丽萍, 等. 细缝算法在细缝结构屏蔽效能计算中的应用[J]. 强激光与粒子束, 2017, 29(7): 50-57. CAO ZHANGSHUAI, LIU QIANG, YAN LIPING, et al. Application of thin-slot formalism methods in calculating shielding effectiveness of thin-slot structure[J]. High Power Laser and Particle Beams, 2017, 29(7): 50-57(in Chinese). [12] 安静, 吴一辉. 开缝腔体场强增强效应抑制方法研究[J].微波学报, 2018, 34(6): 93-96. AN JING, WU YIHUI. Study on the inhibition method of field enhancement effect for the slotted cavity[J]. Journal of Microwaves, 2018, 34(6): 93-96(in Chinese). [13] 郝建红, 蒋璐行, 范杰清, 等. 内置介质板的开孔箱体屏蔽效能电磁拓扑模型[J]. 电工技术学报, 2017, 32(9): 101-111. HAO JIANHONG, JIANG LUXING, FAN JIEQING, et al. Electromagnetic topology model for the shielding effectiveness of an apertured enclosure with a lossy dielectric layer[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 101-111(in Chinese). [14] 方小星, 朱志宇, 张明新, 等. 雷达波对孔缝腔体内复杂传输线耦合影响[J]. 西安电子科技大学学报, 2016, 43(6): 135-140. FANG XIAOXING, ZHU ZHIYU, ZHANG MINGXIN, et al.Coupling influences of the radar electromagnetic field on the complex transmission line in an aperture cavity[J]. Journal of Xidian University, 2016, 43(6): 135-140(in Chinese). [15] 谢金明, 谭博, 王瑞林. 高速数字电路设计与噪声控制技术[M]. 北京: 电子工业出版社, 2003. XIE JINMING, TAN BO, WANG RUILIN. High speed digital circuit design and noise control technology[M]. Beijing: Electronic Industry Press, 2003(in Chinese). [16] 刘益才, 杨智辉, 刘振利, 等. 热声热机谐振管截止频率选择机理[J]. 中南大学学报(自然科学版), 2006(4): 759-762. LIU YICAI, YANG ZHIHUI, LIU ZHENLI, et al. Mechanism of cutoff frequency of resonator tube in thermoacoustic engine[J]. Journal of Central South University (Science and Technology), 2006(4): 759-762(in Chinese). [17] 焦重庆, 李顺杰. 导电板覆盖的开孔矩形腔体电磁屏蔽效能的比较研究[J]. 电工技术学报, 2016, 31(1): 112-118. JIAO CHONGQING, LI SHUNJIE. Shielding effectiveness comparison of a rectangular box with an aperture covered by conductive sheet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 112-118(in Chinese). [18] 夏艳君. 高屏蔽通风波导新型结构研究[D]. 成都: 电子科技大学, 2018. XIA YANJUN. Study on new structure of highly shielding ventilated waveguide[D]. Chengdu: University of Electronic Science and Technology of China, 2018(in Chinese). Application Research of Cut off Waveguide in the Shielding Cavity LIU Zhijian1, TU Zhizhang1, LUO Linglin1, CHEN Xiaoya2, WANG Chang1 (1. Faculty of Electrical Power Engineering, Kunming University of Science and Technology, Kunming 650500, China; 2. Anhui Jinzhai Pumped Storage Co., Ltd., Lu’an 237300, China) Based on the high pass filter performance of waveguide, a metal shielding enclosure with waveguide structure is designed. The HFSS finite element simulation software is used to simulate the rectangular holes andcavity models with a section of rectangular waveguide respectively, and analyzes their shielding effectiveness and electromagnetic field strength changes in the frequency range of 1.0~2.0 GHz. Furthermore, the effects of different polarization directions of plane wave and waveguide length on the shielding effectiveness of the cavity are studied, and it is found that0polarization along theaxis (along the short side) has the best overall shielding effectiveness, and the waveguide length is positively correlated with the cavity shielding effectiveness. The results show that the shielding effectiveness of the cavity with holes can be improved by adding waveguide. When the waveguide length is 6mm, the cut-off frequency of the metal cavity is increased from 1.16 GHz to 1.5 GHz; the resonant frequency of the cavity is obviously reduced, and the resonant times is relatively reduced as well. waveguide; shielding effectiveness; cut-off frequency; cavity resonance 10.3969/j.ISSN.1672-0792.2021.02.010 TM15 A 1672-0792(2021)02-0073-06 2020-07-01 刘志坚(1975—),男,教授,主要研究方向为电力系统运行与控制; 涂志章(1992—),男,硕士研究生,主要研究方向为电磁兼容与机箱电磁屏蔽; 罗灵琳(1983—),女,讲师,主要研究方向为电力系统自动化。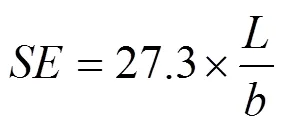
3 基于HFSS有限元方法仿真
3.1 腔体仿真模型

3.2 矩形波导管与矩形孔对比仿真分析


3.3 极化方向对矩形波导管腔体仿真分析
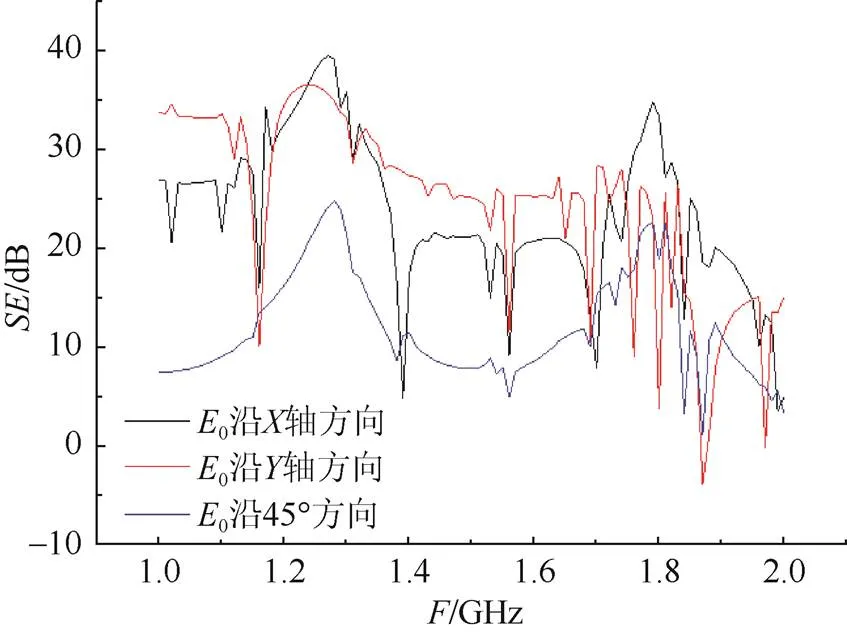
3.4 不同长度的波导管腔体仿真分析
4 结论
