三维模塑互联器件中耦合波导管机械行为的仿真研究
2021-07-03彭煌祁黎揭敢新王俊张志勇郭力
彭煌,祁黎,揭敢新,王俊,张志勇,郭力
(中国电器科学研究院股份有限公司,工业产品环境适应性国家重点实验室,广州 510663)
前言
根据国际数据公司IDC统计和预测,到了2025年,全球每年产生的数字化的数据总量将达到175十万亿亿字节(175 ZB)[1]。如果把175 ZB全部存在DVD光盘中,那么这些光盘叠加起来的高度将是地球和月球距离的23倍,或者绕地球222圈。目前中国的宽带平均下载速度为120.92 Mb/s,一个人要下载完这175 ZB的数据,需要3.75亿年。因此,数据传输速率必须迅速增加,这将通过铜线的电传输推至极限;另一方面,光在光导纤维的传导损耗比电在电线传导的损耗却低得多,而且光纤具有重量轻,抗干扰能力强,工作性能可靠等优点[2]。所以,使用光纤代替铜线是最合理的,这就是为什么越来越多的元器件要在板上和组件上建立光纤连接进行通信的主要原因[3]。然而,光学短程连接目前还不能替代成熟的铜线,特别是由于缺乏与集成波导管的内外耦合的标准SMT(表面安装技术)工艺兼容的简单且稳健的耦合技术,因此,在如今的工业应用中(如工业4.0或物联网)需要新的封装技术[4]。
1 技术原理
光学短程连接的关键应用场景是智能传感器网络,尤其是在航空航天和汽车领域,它们都会使用到结构元件中的集成光学器件,因此,需要将光纤集成到碳纤维增强聚合物(CFRP)中[5]。使用这些波导管的关键是在任意位置上的双向波导耦合,以将不同的传感器模块连接到光子网络上,然而,实现嵌入式的波导管的输入和输出耦合是极具挑战性的,目前最通常的方法是在结构的边缘或者切口处通过碰撞对接实现波导管的耦合[6,7]。但这种方法对于现场组装来说是效率很低的,并且波导管的切口会影响碳纤维增强聚合物结构的完整性;另外,这种对接耦合方法的另一个缺点是需要中断两个波导的传输[8]。
基于以上的分析,为了克服这些缺点,现阶段有一种更为科学的方法对这类双向波导管进行耦合,该技术名为波导管的不对称芯-芯耦合(ACCC)技术,原理就是通过使两个不对称的波导管(一根为刚性波导管,一根为柔性波导管)的芯的上底面和下顶面进行接触,从而实现两个波导的双向连接而不会中断[9]。为了确保将多个模块耦合到总线,重要的一点是在总线到模块方向上具有适度的耦合比,以在总线中保持足够的能量以进一步耦合,同时还希望从模块到总线耦合尽可能多的能量,以确保对于传感器信号的低衰减;另外,这种耦合的方式没有固定的耦合比,也就是说它可以根据需要来调整两根波导管的接触长度来实现不同的耦合比[10]。
2 仿真需求
图1 是不同接触面积下两根波导管中光信号耦合状态的区别——沿着接触区域,由于缺少折射界面,光从一个波导管耦合到另一个波导管中,以确保全反射[11]。由图可知,接触面积决定了波导宽度和接触耦合长度,通过增加接触长度,可以有较高概率将较低阶信号耦合到第二根波导管中;同时,可以通过调节该处耦合长度来调整耦合比,将不同信号电平的不同传感器模块连接到总线波导。因此,也需要通过在耦合点处弯曲耦合配对来实现不对称耦合比,以增加波导管耦合后输出的光量。
图2 是波导管的不对称芯-芯耦合技术的原理图,该技术同时存在柔性和刚性的两种耦合波导管,可以在基板上或者模块层面上实现[12]。刚性波导管用作总线,可嵌入电光印刷电路板或碳纤维增强聚合物作为元件;而另一根波导管搭建在柔性基板(例如PEN箔)上,并且可以安装在电光收发器模块上[12,13]。在耦合点处,需要去除两个波导的包层以使芯接触,通过使用箔(具有适应的折射率)作为包层来确保任意的耦合位置,其可以被临时移除用于耦合。通过在耦合点上施加预定义的力,可以根据耦合长度的变化调节耦合比[14,15]。这里所提出的耦合概念确保了不对称的双向连接,而且没有任何波导的中断;此外,根据信号强度,可以由单个波导提供多个模块和连接,虽然光信号部分地耦合到模块,但它也保留在主波导中以实现进一步耦合[12-15]。
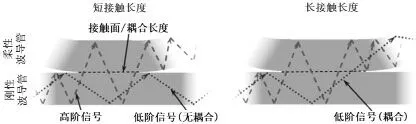
图1 不同接触面积下两根波导管芯的耦合[11]
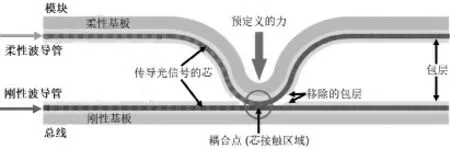
图2 波导管的不对称芯-芯耦合技术原理图[15]
综上所述,耦合长度的变化会直接影响到耦合比的变化,进而影响到耦合波导管中光信号的传输。因此,我们有必要研究在波导管耦合的过程中,有哪些因素会影响到耦合长度。这些因素可能包括,波导管的材料,波导管的形状或者是波导管耦合的竖直位移等等。同时也需要知道在耦合的过程中是否会对波导管的芯造成损害。为了对上述问题进行探究,需要对多种不同外型的波导管模型进行研究,同时还需要利用控制变量法研究不同的影响因素,因此实验式的研究会产生巨大的花费。基于这个原因采用计算机的方式模拟真实的模型,进而再对一系列不同的模型进行仿真分析,能够更加经济和有效地研究上述问题。另一方面,基于计算机方式的研究还提供了更为细致不同区域离散度的耦合结果,这些结果可以随着时间的推进和条件的不同进行逐步地影响的观察。这些都是实验式的研究所无法带来的结果,因此本次工作将采用计算机对柔性和刚性波导管的耦合进行仿真分析,以期能得到合理的分析结果。
3 仿真过程
本研究先使用NX软件对所要进行仿真的波导管进行三维建模,之后将建模文件导入ANSYS软件进行仿真分析。
3.1 模型创建
首先需要简化模型,模型中有些不必要的部件或者是生产工艺所需的结构造型是可以简化的。比如模型中波导管的芯的外壳就可以在仿真中省去,因为这部分并不会影响仿真结果。通过简化模型,可以使得仿真的过程更加快速,并且能在仿真中更好地关注重点的区域。
其次,需要建立几个模型的对照组进行仿真研究,如图3所示,在本次仿真研究中,利用NX三维建模软件创建了四个不同的波导管不对称芯-芯耦合模型的对照组,它们分别是:
1)刚性波导管是平直的,柔性波导管为曲率半径为5 mm的弯曲波导管;
2)刚性波导管是平直的,柔性波导管为曲率半径为10 mm的弯曲波导管;
3)刚性波导管是平直的,柔性波导管为曲率半径为20 mm的弯曲波导管;
4)刚性波导管是任意弯曲的,柔性波导管为曲率半径为5 mm的弯曲波导管。
3.2 网格剖分
在本次仿真中,整个模型的最小尺寸是0.1 mm,只有两个主要部件。首先是波导管的基板,是直接与研究对象波导管芯接触的,且为规则的模型,因此可采用单元边长为0.03的六面体对其进行网格的映射划分。然而,映射划分只适用于规则的几何图素,对于裁剪曲面或者空间自由曲面等复杂几何体难以控制。自由网格划分用于空间自由曲面和复杂实体,采用三角形,四面体进行划分,采用网格数量、边长及曲率来控制网格的质量。在本次仿真中,波导管芯的模型就是一个复杂的几何体,而且是主要的研究对象,因此采用了边长为0.01 mm的四面体来对其进行网格的剖分。
3.3 材料定义
在本次仿真中,需要定义两种材料。首先波导管的基板所采用的是聚甲基丙烯酸甲酯(PMMA),具有高透明度,密度比玻璃低大约是1.15~1.19 g/cm3,强度较高,抗拉伸和抗冲击能力比普通玻璃高7~18倍,熔点约为130~140 ℃;波导管的芯采用的是特定的由高分子组成的呈胶状物质的光敏树脂材料,在紫外线照射下,这些分子结合成长长的交联聚合物高分子。在成键时,聚合物由胶质树脂转变成坚硬物质,具体参数如表1。
3.4 边界条件设置
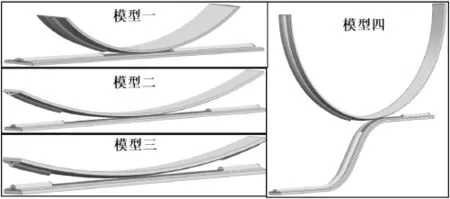
图3 四组不同的波导管不对称芯-芯耦合模型图
首先是模型的受力设置,波导管的不对称芯-芯耦合模型主要是柔性波导管的基板上表面受到一个竖直向下的预定义的力,这个力控制着柔性波导管在竖直方向上的位移,从而改变两根波导管芯之间的接触面积。其次是约束设置,在刚性波导管的基板的下表面添加一个固定约束,使得整根刚性波导管为零自由度;另外,在实际运作中,柔性的波导管只会进行向下的运动,并不会在水平方向上产生位移也不会在任意方向产生旋转。所以,应当对柔性波导管的六个自由度当中的五个自由度进行固定约束,使得它们只能在竖直方向进行运动,并且位移距离也不能超过波导管芯的半径的距离。
3.5 求解仿真结果
在设置完一系列的条件之后,最后设定仿真所需的输出结果,例如模型的形变结果,模型的应变结果以及模型的应力结果等等。图4是模型一的应变云图的变化过程。从图中可以直观地看到两根波导管的芯在接触过程中的应变变化,以及形变发生的过程。另外,除了进行这样纵向的对比,由于设置了对照组,还能够进行横向的对比,图5是模型一、模型二、模型三的刚性波导管的应变云图的结果。
4 结果分析
在得到所有对照组的波导管不对称芯-芯耦合模型的仿真结果之后,对研究数据进行整理和绘制对应的曲线图进行比较和分析。
如图6所示,横坐标代表柔性波导管与刚性波导管在竖直方向的耦合深度,纵坐标代表柔性波导管与刚性波导管接触区域的长度。可以明显地看出,在同样的耦合深度的情况下,曲率半径为5 mm的柔性波导管与刚性波导管的接触长度最短;而曲率半径为20 mm的柔性波导管与刚性波导管的接触长度最长。但是另一方面,随着柔性波导管的曲率半径增大并且耦合深度增大,大曲率半径的柔性波导管与刚性波导管的接触长度增长的优势也在减弱:如图6所示,比如在耦合深度大于0.04 mm之后,曲率半径为20 mm的柔性波导管的接触长度与曲率半径为10 mm的柔性波导管的接触长度已经相差无几了。综上所述,如果只考虑要得到更大的耦合比的情况下,选用曲率半径较大的柔性波导管与硬性波导管耦合无疑是最合适的。在同样的耦合深度的情况下,曲率半径大的柔性波导管与硬性波导管的接触长度更长。所以可以调节的接触长度更多,也就是说能得到更多更大的耦合比。
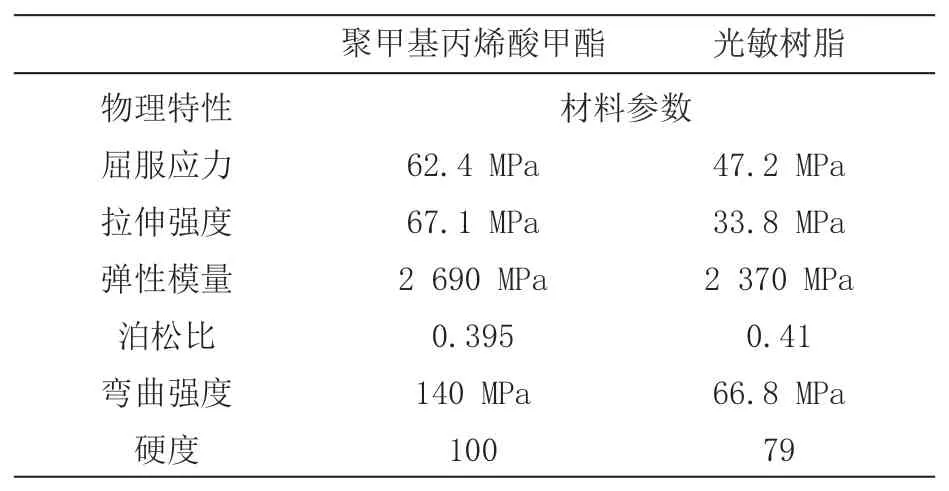
表1 波导管中各部件的材料参数

图4 模型一的应变云图的变化过程

图5 模型一/二/三中刚性波导管的应变云图的比较
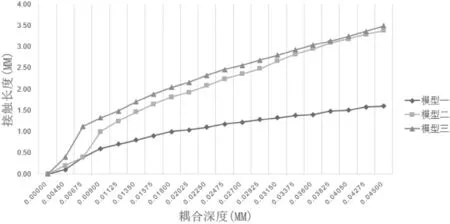
图6 模型一/二/三接触长度与耦合深度的关系曲线
如图7所示,横坐标代表柔性波导管与刚性波导管在竖直方向的耦合深度,纵坐标代表柔性波导管与刚性波导管接触区域的长度。可以明显地看出,在同样的耦合深度的情况下,直线型的刚性波导管与柔性波导管的接触长度更长;而弯曲的刚性波导管与同样的柔性波导管的接触长度更短。而且,随着耦合深度的加大,直线型的刚性波导管与柔性波导管的接触长度的增长优势更加明显。如图所示,比如,在耦合深度只有0.009 mm的时候,直线型的刚性波导管的接触长度只比弯曲刚性波导管的接触长度长大约0.4 mm;但是在耦合深度达到0.045 mm的时候,直线型的刚性波导管的接触长度就比弯曲刚性波导管的接触长度长大约0.8 mm。综上所述,如果只考虑要得到更大的耦合比的情况下,选用直线型的刚性波导管与柔性波导管耦合无疑是最合适的。在同样的耦合深度的情况下,直线型的刚性波导管与柔性波导管的接触长度更长。因此可以调节的接触长度更多,也就是能得到更大的耦合比。
如图8所示,横坐标代表柔性波导管与刚性波导管在竖直方向的耦合深度,纵坐标代表柔性波导管与刚性波导管耦合时产生的应变。图表三条曲线分别代表波导管的芯耦合时的应变随着耦合深度的增加而增大。可以明显地看出,在同样的耦合深度的情况下,曲率半径为5 mm的柔性波导管与刚性波导管耦合产生的应变最小;而曲率半径为20 mm的柔性波导管与刚性波导管耦合产生的应变最大。但是另一方面,随着柔性波导管的曲率半径的增大,波导管耦合时产生的应变的差异在减小。比如在耦合深度同为0.045 mm时,曲率半径相差为5 mm的模型二和模型一分别在耦合时产生的应变相差大约为0.5 mm/mm;而曲率半径相差为10 mm的模型三和模型二分别在耦合时产生的应变相差大约只有0.2 mm/mm。如果波导管的芯在耦合时应变过大,就可能会导致芯产生塑性形变,进而造成波导管的永久性的结构损害,从而影响光在波导管中的传播。综上所述,在满足耦合比的情况下,选用曲率半径较小的柔性波导管更为合适。因为在同样的耦合深度的情况下,曲率半径较小的柔性波导管与硬性波导管耦合时产生的应变更小,这样子可以提高波导管的使用寿命和稳定性。
如图9所示,横坐标代表柔性波导管与刚性波导管在竖直方向的耦合深度,纵坐标代表柔性波导管与刚性波导管耦合时产生的应变。图表两条曲线分别代表波导管的芯耦合时的应变随着耦合深度的增加而增大。可以看出,在同样的耦合深度的情况下,直线型的刚性波导管与柔性波导管耦合时产生的应变,和弯曲的刚性波导管与同样的柔性波导管耦合时产生的应变相差无几。比如在耦合深度小于0.029 25 mm,两个模型的应变变化曲线几乎重叠在一起。综上所述,对于相同的柔性波导管,刚性波导管的形状对于耦合过程中产生的应变的影响不大。
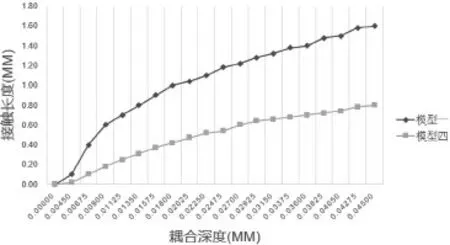
图7 模型一/四接触长度与耦合深度的关系曲线
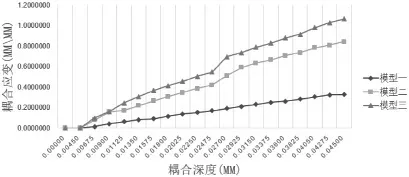
图8 模型一/二/三耦合应变与耦合深度的关系曲线
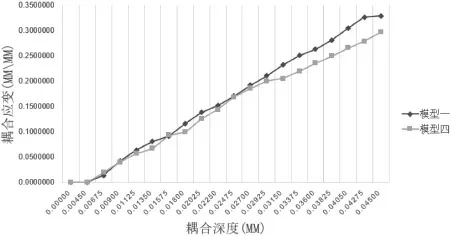
图9 模型一/四耦合应变与耦合深度的关系曲线
5 结论
通过以上的仿真研究,可以得出以下总结和建议:
在波导管的不对称芯-芯耦合技术中,如果要获得尽可能大的芯的耦合比的话,就需要选择曲率半径更大的柔性波导管进行耦合;但是如果在已经满足了最大耦合比的情况下,可以尽量选择较小曲率半径的柔性波导管,这样可以减小波导管耦合时的应变和应力,从而增加波导管的使用寿命和稳定性。最后,应尽量避免使用非直线型的刚性波导管作为总线进行耦合。
