基于机会约束的微电网混合整数规划优化调度

晏开封，张靖，何宇，张英，刘影，李兴莘

基于机会约束的微电网混合整数规划优化调度

晏开封1，张靖1，何宇1，张英2，刘影3，李兴莘1

（1. 贵州大学 电气工程学院，贵州 贵阳 550025；2. 贵州电网公司 电力科学研究院，贵州 贵阳 550002；3. 贵州电网公司 电网规划研究中心，贵州 贵阳 550002）

为解决微电网短期及超短期优化调度问题，考虑微电网运行过程中不确定因素的影响。以最小化微电网运行成本为目标，综合考虑功率平衡、机会约束等约束条件，提出了一种基于机会约束的微电网混合整数规划优化调度模型。针对模型中机会约束确定性转化问题，采用基于采样的机会约束条件确定性转化方法，将机会约束变为混合整数线性约束。同时，为了提高计算速度，将目标函数中的非线性函数进行分段线性化。算例结果表明，基于机会约束的微电网混合整数规划优化调度模型具有较好的可行性和有效性。

不确定因素；机会约束；采样确定性转化；分段线性化；混合整数线性规划

0 引言

当前全球能源安全、环境污染等问题日益严重，优先开发利用风能、太阳能等可再生能源是保护环境，减少对化石能源依赖的重要途径[1-4]。与此同时，微电网作为由分布式能源、储能装置、负荷等构成的小型电力系统，可以实现本地能源协调，减少能源损耗，使其成为电网的重要组成部分，其经济运行与优化调度是重要的研究内容[5-6]。

由于微电网运行过程中受多种不确定因素的影响[7]，使微电网优化调度面临严峻的挑战。因此，如何应对微电网中的不确定性成为微电网优化调度亟待解决的问题。当前微电网中考虑不确定因素的调度方法有很多种，应用最广泛的分别是随机优化和鲁棒优化。鲁棒优化是寻求最恶劣场景下的优化调度方案[8-10]，所得的调度方案过于保守。随机优化是利用不确定变量的概率分布函数进行优化求解[11-13]，能够较好地满足方案的经济性和鲁棒性。其中机会约束是一种解决含有不确定因素的微电网优化调度较好的方法[14]，但在模型求解过程中机会约束的处理耗费时间过长，导致整个模型求解速度较慢，通常无法在指定时间内得到调度结果。

将机会约束转化为确定性约束可以提高模型的求解速度，可以采用的转化方法有很多种，比较常用的有随机模拟法和解析法。随机模拟法计算速度较慢，通常无法满足微电网的超短期优化调度。解析法一般只能解决单个随机变量，当含有多个随机变量时，解析法不能解决此类问题。因此，一般采用估计方法对多个随机变量和的累积分布函数进行估计。文献[15]采用Copula函数求出预测误差和的概率密度函数，进而完成确定性转化。文献[16]通过Copula核估计函数将联合概率约束转换成确定性约束，进一步减少估计过程中产生的误差。文献[17]通过求取随机变量分布和的前3阶矩得到累计概率分布函数，然后用两点估计法对其进行估计。上述方法虽然能够解决含有多个随机变量的问题，但是求解过程中存在估计函数，估计函数的选择通常依赖经验会产生误差，如果估计函数选择不当，对求解结果会造成较大的影响，无法保证结果的准确性。

本文基于采样理论将机会约束转化为混合整数约束，可以更好地解决包含多个不确定变量的机会约束转化成确定性约束的问题，由于该模型中的随机变量与优化变量可以分离，故对模型进一步简化。为了提高模型计算速度，将模型中柴油发电机燃油成本函数分段线性化，使整个模型由混合整数非线性规划（mixed integer nonlinear programming，MINLP）问题转化为混合整数线性规划（mixed integer linear programming，MILP）问题求解。算例结果表明，在保证计算精度合理的情况下，基于机会约束的微电网混合整数规划优化调度模型具有较快的计算速度。

1 分布式电源数学模型

1.1 不可控分布式电源模型

由于风光出力的不确定性，故一般测得的预测值具有较大预测误差[18]。风电与光伏输出功率的预测误差一般采用正态分布[18-19]。

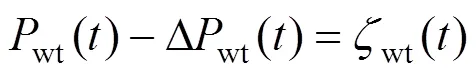
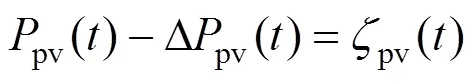
式中：Δwt()、Δpv()分别为风、光出力与负荷在时段的预测误差；wt()、pv()分别为两者的预测值；wt()、pv()分别为两者的实际值。

1.2 可控分布式电源模型

1.2.1 柴油发电机

柴油发电机在运行过程中产生的燃料成本如下所示：

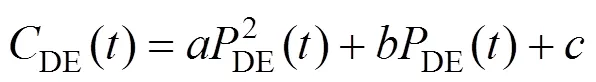
式中：DE()为时段柴油发电机燃油成本；DE()代表柴油发电机在时段的输出功率；为柴油发电机相应的系数。

1.2.2 蓄电池模型

蓄电池作为储能设备，在可再生能源不足的情况下将储存的能量释放出来充当稳定电源，保证系统的稳定运行。其充放电过程如下：

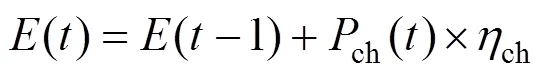
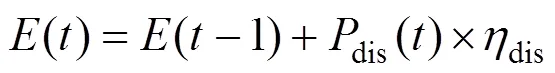
式中：ch()和dis()为蓄电池在时段的充、放电功率；()为蓄电池时段的剩余容量；ch和dis为充放电效率。

2 基于机会约束的微电网优化调度模型

2.1 目标函数

风力发电、光伏发电无法控制，其运行成本难以调整，可忽略不计。故在并网模式下，微电网运行成本包含柴油发电机的运行和维护成本、微电网与大电网购售电成本、蓄电池维护成本、系统旋转备用成本以及污染物处理成本。

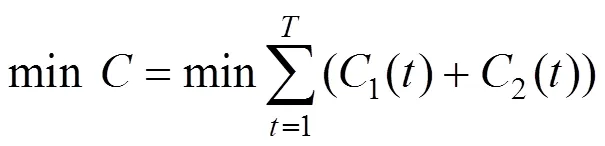
式中：为微电网系统总运行成本；1()和2()分别为微电网在时段的经济成本和环境成本。

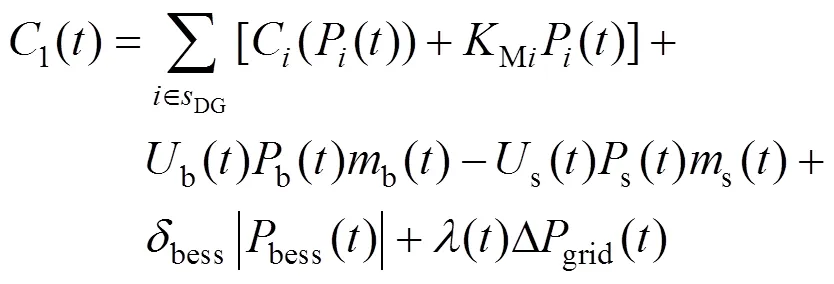
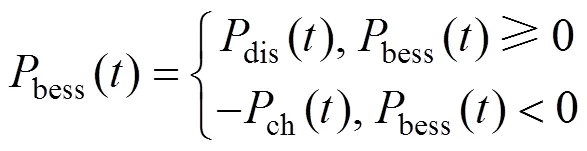
式中：为柴油发电机编号；DG为柴油发电机集合；P()为柴油发电机的输出功率；C(P())为柴油发电机的燃料成本；Mi为柴油发电机的运维系数；b()和s()分别为微电网在时段向大电网的购售电功率；b()和s()分别为微电网在时段向大电网的购售电状态；b()和s()分别为微电网在时段与大电网购售电价；bess为蓄电池的折旧系数；bess()为蓄电池在时段的出力，视其充放电状态而定；Δgrid()为微电网在时段向大电网购买的旋转备用容量；()为在时段大电网旋转备用电价。

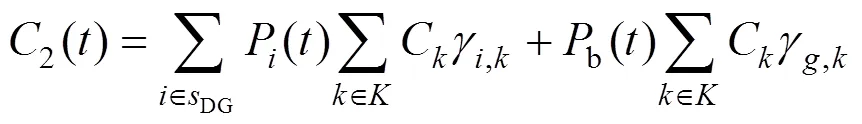
式中：为污染气体集合；,k(g/kW·h)为微电网中柴油发电机生产单位电能时第类污染物的排放系数；C为第类污染物的环境治理成本；,k(g/kW·h)为微电网中可控机组生产单位电能时污染物的排放系数。

2.2 约束条件

功率平衡约束：

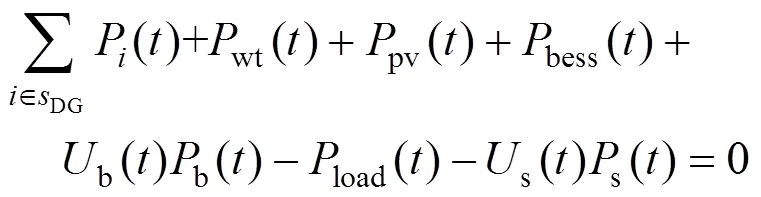
柴油发电机输出功率上下限约束：

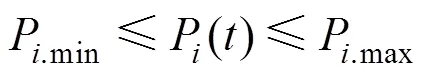
式中：P.min、P.max为柴油发电机输出功率的上下限。

微电网与大电网传输功率约束：

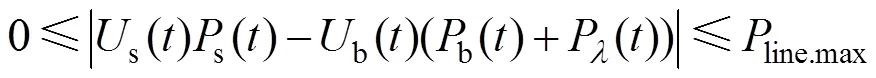
式中：line.max为微电网与大电网间最大传输功率。

购电及售电状态约束：

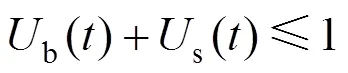
柴油发电机爬坡率约束：

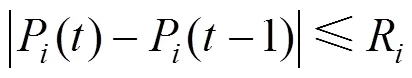
式中：P(–1)为上一时段柴油发电机的出力；R为柴油发电机爬坡率上限。

蓄电池约束：

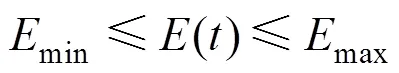
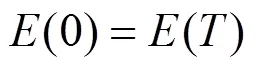
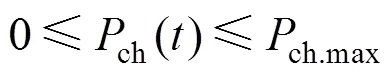
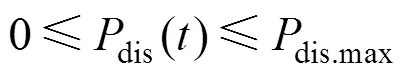
式中：min、max分别为蓄电池容量的上下限；ch.max、dis.max分别为蓄电池充、放电功率的上限。

旋转备用约束：

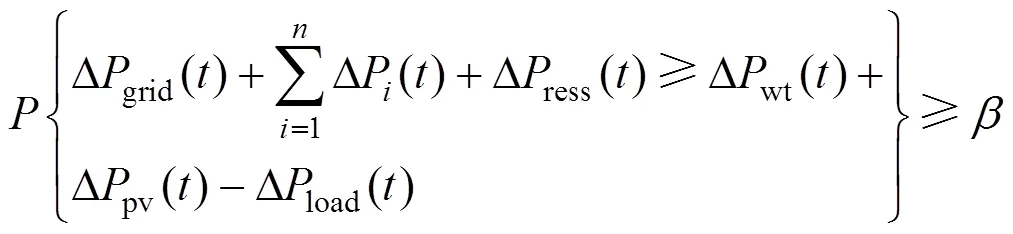
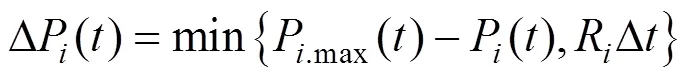
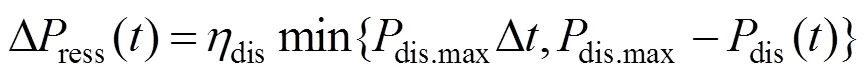
式中：DP()代表柴油发电机在时段可以提供的备用容量，其值由柴油发电机在时段剩余可发电量与其分钟级爬坡速率共同决定，Δ取5 min；Δress()为微电网内蓄电池在时段可以提供的备用容量，由该蓄电池分钟级最大放电额度与其在时段的剩余可放电量共同决定。

3 模型求解

为了加快模型计算速度，减少模型求解时间，本文采用分段线性化对模型中的非线性部分进行处理，将MINLP模型转化为MILP模型进行求解。

3.1 柴油发电机燃料成本的线性化

由于本文目标函数中的柴油发电机成本是其出力的一元二次函数，因此，采用分段线性化函数对其线性化[20]，将其分成段进行线性逼近，然后再引入一个状态变量()和个连续变量P()表示线性化函数，如图1所示。

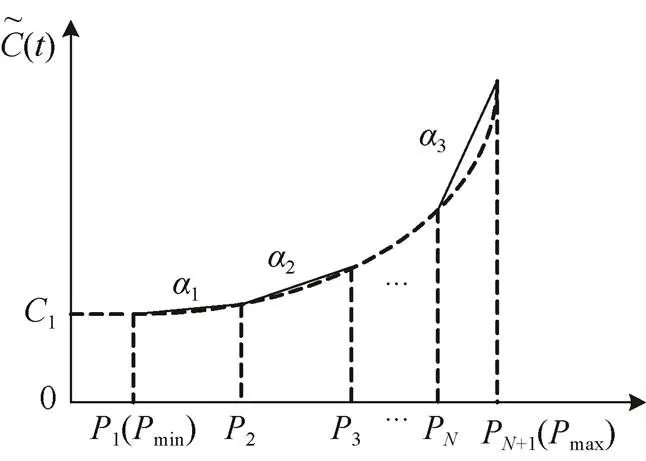
图1 柴油发电机燃料成本线性化

线性化后的函数表达式如下：

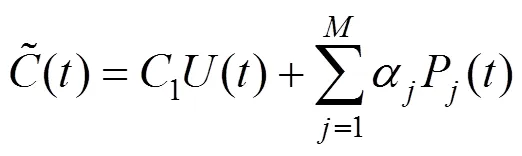
其中，

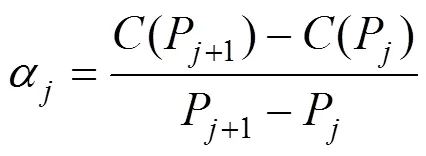
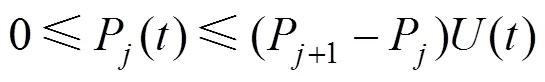
3.2 机会约束条件转化

机会约束在求解过程中需要先进行采样，再将采样样本代入式中进行判断约束条件是否成立，判断过程过于耗时，导致模型求解速度很慢。因此，将机会约束进行确定性转化可以减少求解时间。本文采用基于采样的机会约束规划条件确定性转化方式[21]，这种方法在转化过程中不需要使用累积概率分布函数，直接可以将机会约束进行确定性转化，模型求解时无需对机会约束成立与否进行判断，因此计算速度有较大地提升。

利用蒙特卡洛模拟处理式（19）的机会约束条件时，需要从随机变量的概率分布函数中采取大量样本，用这些样本验证式（25）是否成立，对成立的次数进行统计。若机会约束条件式（25）验证次数与置信度的乘积大于或等于成立次数，则式（25）成立；反之式（25）不成立。

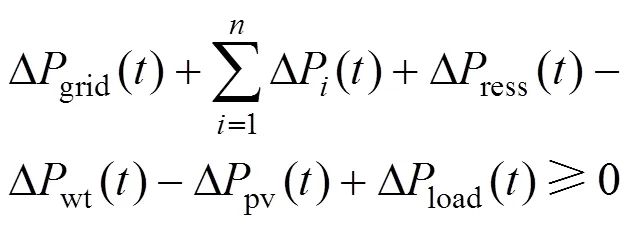
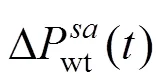
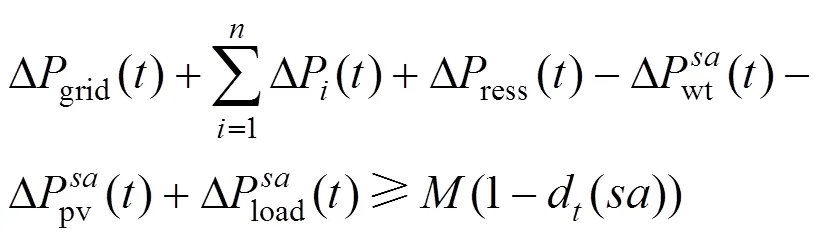
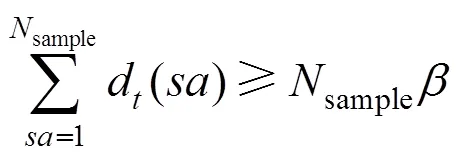
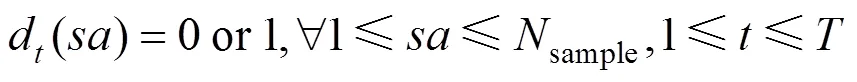
式中：取一个比较小的负数。

当d()=1时，对于采样的第个样本，式（29）成立；当d()=0时，对于采样的第个样本，式（29）不成立。

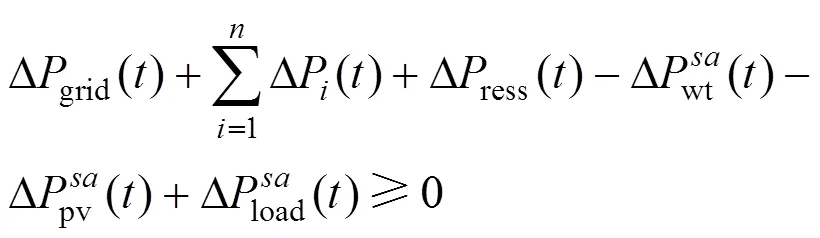
由式（27）的约束可知，如果采样sample次，则式（29）至少成立sample次，即转化后的约束条件式（26）~（28）与机会约束条件式（19）等价。如果采样样本足够大，对所有的机会约束条件都满足式（19）与式（26）~（28）的确定性转化条件，即把机会约束转化为混合整数线性约束。此时，把原来的个机会约束条件转化为sample个混合整数约束条件，同时引入sample个[0-1]变量。结合模型特点，式（19）中的随机变量和优化变量可以进行分离，所以按照影响式（26）成立程度的大小对采样所得的样本值重新进行排序，可以使式（26）~（28）进一步简化，得到的等效约束条件如式（30）~（32）所示。

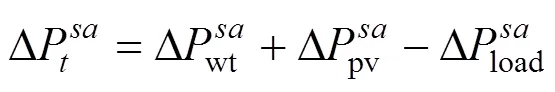
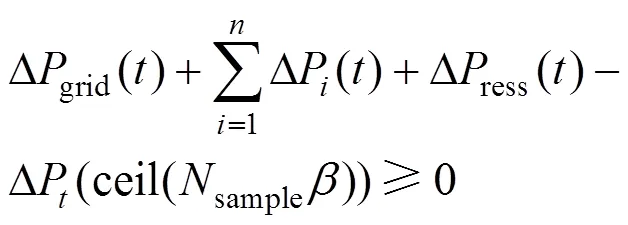
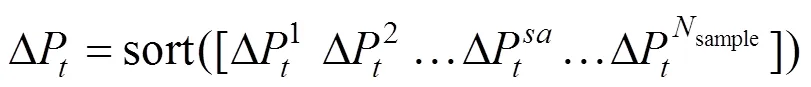
式中：ceil(*)和sort(*)分别表示为向上取整函数和升序排列函数，即ceil(*)可以得到大于或等于*的最小整数，sort(*)可以将相量*从小到大进行排列。

3.3 模型求解步骤

综上，本文模型中部分非线性函数全部转化为线性函数，该优化问题由一个MINLP问题变成MILP问题，对此问题，基于MATLAB利用YALMIP建模工具，调用CPLEX进行求解，步骤如下：

（1）输入数据，包括微电网购售电价、旋转备用电价，风机、光伏、负荷出力预测值等。

（2）将非线性的柴油发电机燃料成本函数通过分段线性化变成线性函数，对机会约束进行确定性转化。

（3）采用YALMIP对目标函数与约束条件进行建模。

（4）调用CPLEX求解，输出最优的调度结果。

4 算例分析

4.1 算例介绍

本文选取一个实际微电网作为算例，其中包含两台柴油发电机，光伏、风电、蓄电池各一台。微电网的典型日风、光和负荷预测数据如图2所示；分布式电源运行参数见表1；污染物排放系数及成本见表2；储能参数见表3；微电网与大电网交易电价见表4。

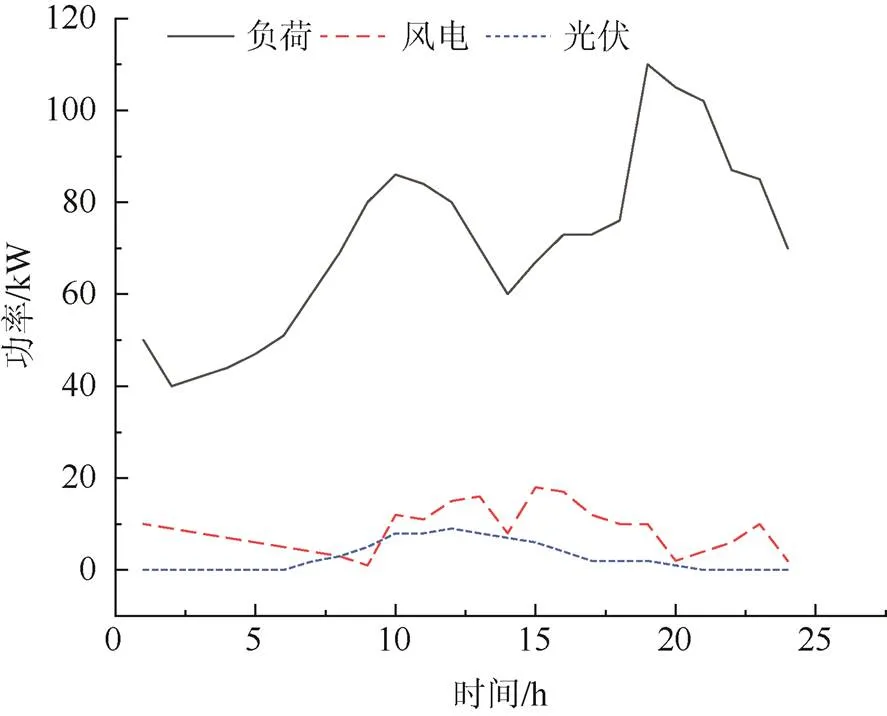
图2 风电、光伏发电和负荷曲线

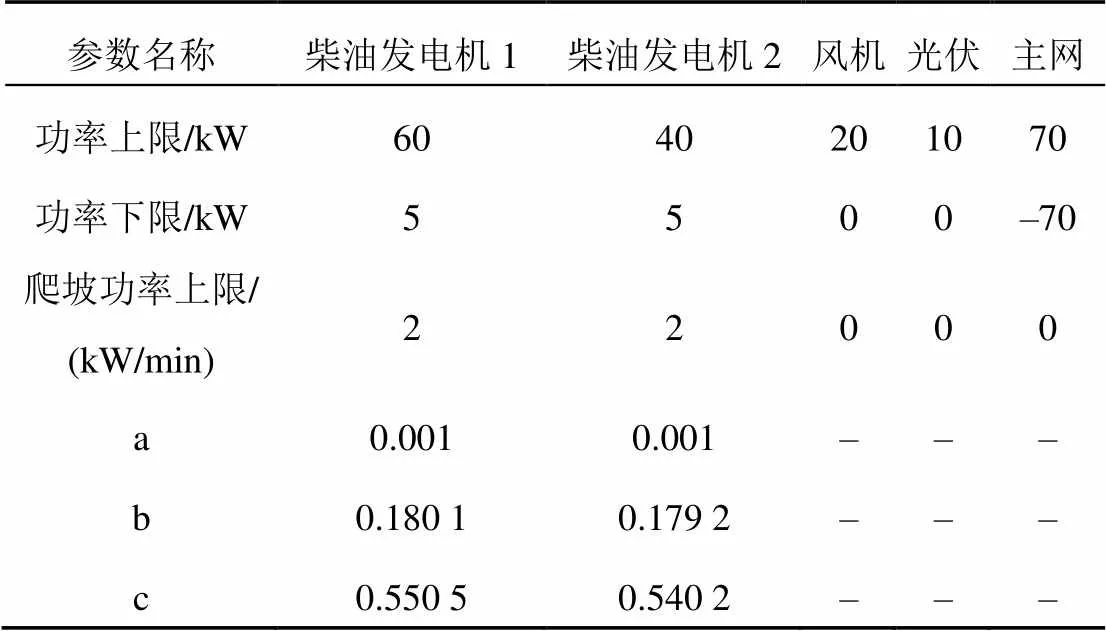
表1 分布式电源参数

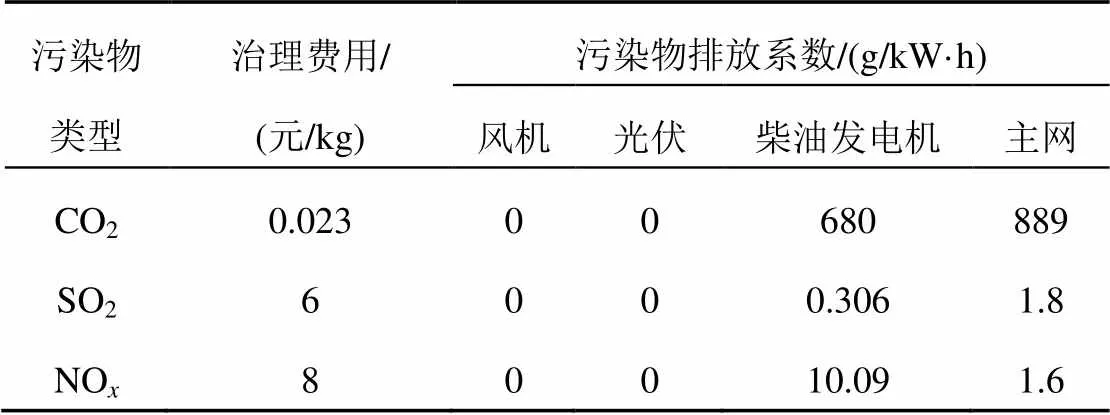
表2 污染物排放系数及成本

本文算例实行分时电价政策，峰时段为11:00—15:00和18:00—21:00，平时段为8:00—10:00和16:00—17:00以及22:00—23:00，谷时段为24:00—7:00，分时交易电价如表4所示。

表3 储能参数

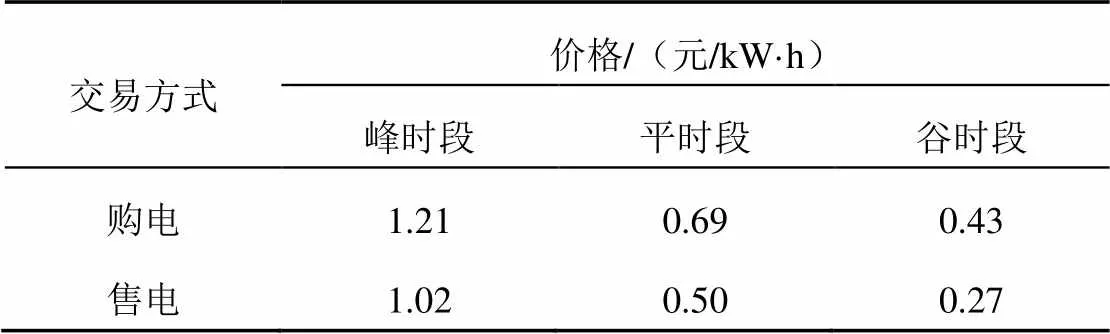
表4 微电网购售电分时电价表

4.2 计算结果分析

采用YALMIP和CPLEX求解线性化后的MILP模型和MINLP模型，计算结果如表5所示，可控分布式电源的出力曲线分别如图3、图4所示。

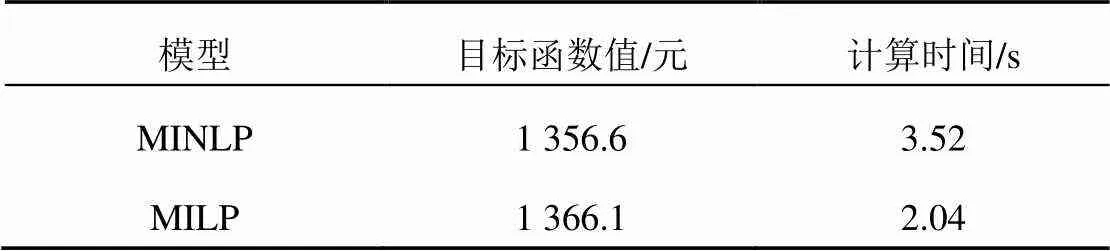
表5 两种模型求解结果对比

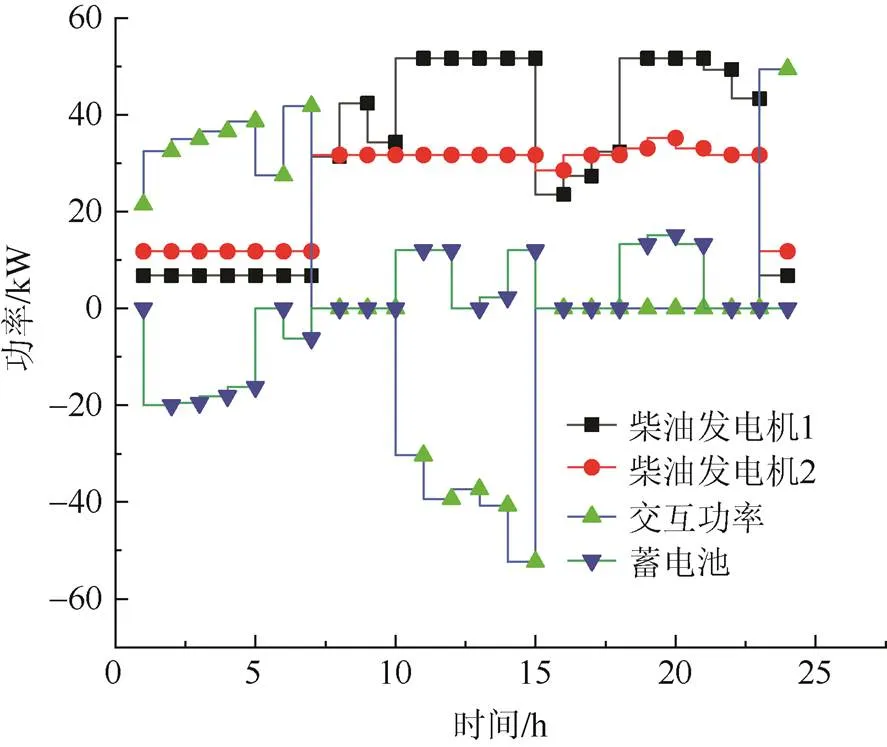
图3 MINLP模型可控电源的调度出力

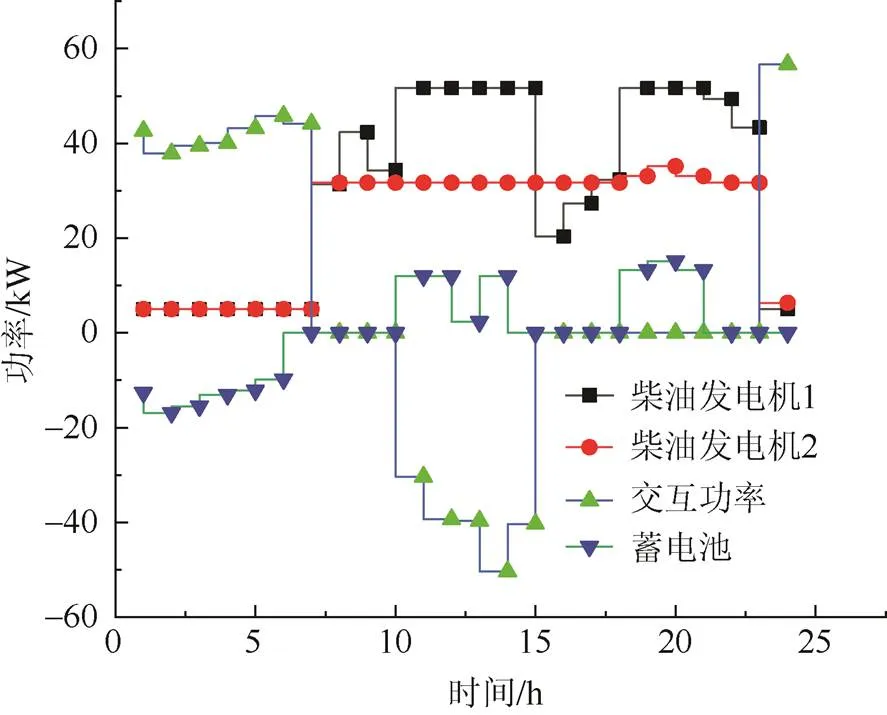
图4 MILP模型可控电源的调度出力

由表5可以看出，从两种模型目标函数值方面对比，MILP模型虽略高于MINLP模型，但准确度很高。从计算时间方面对比，MILP模型明显少于MINLP模型，求解速度快。

总之，用线性模型代替非线性模型，虽然计算精度略差一些，但大幅提升了求解速度，适用于微电网的短期和超短期调度。

从图3和图4可以看出，MILP和MINLP两种模型求解得到的出力曲线变化趋势基本一致。柴油发电机在丰时段尽量发电满足负荷需求，多余的电量卖给大电网。微电网在谷时段进行买电，峰时段进行卖电。蓄电池在谷时段进行充电，峰时段进行放电，利用峰时段和谷时段电价的差值减少微电网的运行成本。MILP和MINLP两种模型的求解结果完全符合微电网经济运行的和优化调度的规律，也进一步验证了本文模型具有较好的可行性和有效性。

4.3 计算性能分析

为了比较本文采用的基于采样的机会约束确定性转化方法和分段线性化方法的可行性和优越性，故用所提方法与粒子群算法（partical swarm optimization，PSO）作对比，结果如表6所示。为能更好地体现微电网系统的动态调度，以1天内的24个时段为调度周期，每个时刻采样1 000次，所设PSO相关参数如下：种群规模设定为1 000，迭代次数设定为300，使用动态变化的惯性权重，惯性权重随着迭代次数线性减小，初始值0.9，终止值0.4，自知学习因子、社会学习因子均取2.05，取10次运行结果的最好值，算例使用MATLAB R2014b编程寻优。两种方法的性能比较如表6所示。

表6 计算性能对比

从表6可以看出，在精度方面本文方法所得结果比采用PSO得到的结果低，但是结果很接近，误差较小，这是由于采用PSO方法寻优，当采样规模足够大时，可以认为机会约束条件的求解过程不存在原理性的误差。而在计算速度上本文方法显著优于PSO，这是由于模型求解最耗时的部分是机会约束条件的成立与否的判断过程，而PSO方法由于每次判断需要先产生样本再做统计，因而模型求解时间最长。综合考虑以上两个方面可知，在保证最优解精度合理的前提下，本文方法比PSO更加具有优势，能够准确快速地去求解微电网的超短期优化调度问题。增加采样样本数可以降低机会约束条件的转化误差，由于简化过程的存在，增加采样数量对计算时间不会有显著影响。

5 结论

在考虑微电网运行过程中不确定因素的影响下，本文建立了基于机会约束的微电网混合整数规划优化调度模型，主要针对机会约束条件中不确定因素的处理和非线性模型进行线性化进行研究。选取了一个实际微电网作为算例，将本文方法与PSO进行了对比，对比结果显示，本文采用基于采样的机会约束确定性处理方法以及分段线性化方法在保证合理精度的前提下，计算速度具有很强的优势，为微电网的超短期调度问题提供了快速有效的方法。

[1] 舒印彪, 薛禹胜, 蔡斌, 等. 关于能源转型分析的评述(一)转型要素及研究范式[J]. 电力系统自动化, 2018, 42(9): 1-15. SHU YINBIAO, XUE YUSHENG, CAI BIN, et al. A review of energy transition analysis: Part one elements and paradigm[J]. Automation of Electric Power Systems, 2018, 42(9): 1-15(in Chinese).

[2] 舒印彪, 薛禹胜, 蔡斌, 等. 关于能源转型分析的评述(二)不确定性及其应对[J]. 电力系统自动化, 2018, 42(10): 1-12. SHU YINBIAO, XUE YUSHNEG, CAI BIN, et al. A Review of energy transition analysis: part two uncertainties and approaches[J]. Automation of Electric Power Systems, 2018, 42(10): 1-12(in Chinese).

[3] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904. ZHOU XIAOXIN, CHEN SHUYONG, LU ZONGXIANG, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904(in Chinese).

[4] 舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J]. 中国电机工程学报, 2017, 37(1): 1-8. SHU YINBIAO, ZHANG ZHIGANG, GUO JIANBO, et al. Study on key factors and solution of renewable energy Accommodation[J]. Proceedings of the CSEE, 2017, 37(1): 1-8(in Chinese).

[5] 马天祥, 贾伯岩, 张智远, 等. 基于二层规划的能源互联微电网能量优化调度方法[J]. 电力系统自动化, 2019, 43(16): 34-43. MA TIANXIANG, JIA BOYAN, ZHANG ZHIYUAN, et al. Energy optimal dispatching method of micro-energy internet based on bi-level programming[J]. Automation of Electric Power Systems, 2019, 43(16): 34-43(in Chinese).

[6] 丁明, 楚明娟, 潘浩, 等. 交直流混合微电网运行优化建模与不确定性分析[J]. 电力系统自动化, 2017, 41(5): 1-7. DING MING, CHU MINGJUAN, PAN HAO, et al. Operation optimization modeling and uncertainty analysis for hybrid AC/DC microgrids[J]. Automation of Electric Power Systems, 2017, 41(5): 1-7(in Chinese).

[7] ZIA M F, ELBOUCHIKHI E, BENBOUZID M. Microgrids energy management systems: a critical review on methods, solutions, and prospects[J]. Applied Energy, 2018(222): 1033-1055.

[8] LIU F, BIE Z, WANG X. Day-ahead dispatch of integrated electricity and natural gas system considering reserve scheduling and renewable uncertainties[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2): 646-658.

[9] 戴璐平, 吴薇, 黄蓓雯. 考虑不确定性的分布式家庭并网光伏系统鲁棒优化能量调度[J]. 电力系统保护与控制, 2019, 47(3): 48-55. DAI LUPING, WU WEI, HUANG BEIWEN. Optimal energy scheduling for family grid-connected photovoltaic systems considering uncertainty[J]. Power System Protection and Control, 2019, 47(3): 48-55(in Chinese).

[10] DING T, WU Z, LV J, et al. Robust co-optimization to energy and ancillary service joint dispatch considering wind power uncertainties in real-time electricity markets[J]. IEEE Transactions on Sustainable Energy, 2016, 7(4): 1547-1557(in Chinese).

[11] 李志伟, 赵书强, 刘应梅. 电动汽车分布式储能控制策略及应用[J]. 电网技术, 2016, 40(2): 442-450. LI ZHIWEI, ZHAO SHUQIANG, LIU YINGMEI. Control strategy and application of distributed electric vehicle energy storage[J]. Power System Technology, 2016, 40(2): 442-450(in Chinese).

[12] 赵书强, 王扬, 徐岩, 等. 基于机会约束目标规划的高风电接入比例下大规模储能与火电协调调度[J]. 中国电机工程学报, 2016, 36(4): 969-977. ZHAO SHUQIANG, WANG YANG, XU YAN, et al. Coordinated dispatch of large scale energy storage system and thermal generation in high wind power penetration level system based on chance constrained goal programming[J]. Proceedings of the CSEE, 2016, 36(4): 969-977 (in Chinese).

[13] 杨明, 罗隆福. 计及风电与负荷不确定性的电力系统无功随机优化调度[J]. 电力系统保护与控制, 2020, 48(19): 134-141. YANG MING, LUO LONGFU. Stochastic optimal reactive power dispatch in a power system considering wind power and load uncertainty[J]. Power System Protection and Control, 2020, 48(19): 134-141(in Chinese).

[14] 江岳春, 邢方方, 庞振国, 等. 基于机会约束规划的微网运行备用优化配置[J]. 电力系统保护与控制, 2016, 44(14): 100-106. JIANG YUECHUN, XING FANGFANG, PANG ZHENGUO, et al. Optimization configuration of operating reserve in microgrid based on chance- constrained programming[J]. Power System Protection and Control, 2016, 44(14): 100-106(in Chinese).

[15] 段偲默, 苗世洪, 李力行, 等. 计及预测误差动态相关性的多风电场联合出力不确定性模型[J]. 电力系统自动化, 2019, 43(22): 31-37. DUAN SIMO, MIAO SHIHONG, LI LIXING, et al. Uncertainty model of combined output for multiple wind farms considering dynamic correlation of prediction errors[J]. Automation of Electric Power Systems, 2019, 43(22): 31-37(in Chinese).

[16] 徐玉琴, 陈坤, 李俊卿, 等. Copula函数与核估计理论相结合分析风电场出力相关性的一种新方法[J]. 电工技术学报, 2016, 31(13): 92-100. XU YUQIN, CHEN KUN, LI JUNQING, et al. A new method analyzing output correlation of multi-wind farms based on combination of copula function and kernel estimation theory[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 92-100(in Chinese).

[17] 周玮, 姜汀, 胡姝博, 等. 基于两点估计法的交直流混合系统电压稳定概率评估[J]. 电力系统保护与控制, 2015, 43(5): 8-13. ZHOU WEI, JIANG TING, HU SHUBO, et al. Probabilistic assessment on voltage stability of AC/DC hybrid systems based on two-point estimate method[J]. Power System Protection and Control, 2015, 43(5): 8-13(in Chinese).

[18] 张俊涛, 程春田, 申建建, 等. 考虑风光不确定性的高比例可再生能源电网短期联合优化调度方法[J]. 中国电机工程学报, 2020, 40(18): 5921-5932. ZHANG JUNTAO, CHENG CHUNTIAN, SHEN JIANJIAN, et al. Short-term joint optimal operation method for high proportion renewable energy grid considering wind-solar uncertainty[J]. Proceedings of the CSEE, 2020, 40(18): 5921-5932(in Chinese).

[19] 吕梦璇, 娄素华, 刘建琴,等. 含高比例风电的虚拟电厂多类型备用协调优化[J]. 中国电机工程学报, 2018, 38(10): 2874-2882. LV MENGXUAN, LOU SUHUA, LIU JIANQIN, et al. Coordinated optimization of multi-type reserve in virtual power plant accommodated high shares of wind power[J]. Proceedings of the CSEE, 2018, 38(10): 2874-2882(in Chinese).

[20] 陈泽兴, 张勇军, 许志恒, 等. 计及需求价格弹性的区域能源中心建模与日前优化调度[J]. 电力系统自动化, 2018, 42(12): 27-35. CHEN ZEXING, ZHANG YONGJUN, XU ZHIHENG, et al. Modelling and optimal day-ahead dispatch of district energy centre considering price elasticity of energy loaddemand[J]. Automation of Electric Power Systems, 2018, 42(12): 27-35(in Chinese).

[21] 李志伟, 赵书强, 李东旭, 等. 基于改进ε-约束与采样确定性转化的电力系统日前调度机会约束模型快速求解技术[J]. 中国电机工程学报, 2018, 38(16): 4679-4691. LI ZHIWEI, ZHAO SHUQIANG, LI DONGXU, et al. Fast solving of day-ahead power system scheduling chance-constrained model based on improved ε -constrained and deterministic transform by sampling[J]. Proceedings of the CSEE, 2018, 38(16): 4679-4691(in Chinese).

The Optimal Dispatching of Mixed Integer Programming Based on Opportunity Constraint of Microgrid

YAN Kaifeng1, ZHANG Jing1, HE Yu1, ZHANG Ying2, LIU Ying3, LI Xingshen3

(1. The Electrical Engineering College, Guizhou University, Guiyang 550025, China;2. Power Science Research Institute, Guizhou Power Grid Corporation, Guiyang 550002, China;3. Power grid Planning Research Center, Guizhou Power Grid Corporation, Guiyang 550002, China)

In order to solve the short-term and super-short-term optimal dispatching problems of microgrid, the influence of uncertain factors in the operation process of microgrid is taken into consideration. In order to minimize the operating cost of microgrid, a hybrid integer programming optimization dispatching model based on opportunity constraint is proposed in this paper, taking power balance, opportunity constraint and other constraints into comprehensive consideration. Aiming at the deterministic transformation of opportunity constraints in the model, a deterministic transformation method of opportunity constraints based on sampling is adopted to transform the opportunity constraints into mixed integer linear constraints. At the same time, in order to improve the calculation speed, the nonlinear function in the objective function is piecewise linearized. The results show that the hybrid integer programming optimization dispatching model based on opportunity constraint is feasible and effective.

uncertainty factor; opportunity constraint; sampling deterministic transformation; piecewise linearization; mixed integer linear programming

10.3969/j.ISSN.1672-0792.2021.02.003

TM73

A

1672-0792(2021)02-0017-08

2020-11-16

国家自然科学基金（51867005）

晏开封（1995—），男，硕士研究生，研究方向为微电网优化调度；

张 靖（1979—），男，教授，研究方向为电力系统稳定、运行与控制等；

何 宇（1978—），女，副教授，研究方向为电力系统规划、电力系统稳定与运行等；

张 英（1978—），女，教授级高级工程师，研究方向为高压电气设备绝缘在线监测及故障诊断、绝缘材料应用以及大气压等离子体；

刘 影（1978—），男，高级工程师，主要研究方向为电力系统规划；

李兴莘（1995—），男，硕士研究生，研究方向为电力系统运行与控制。

张 靖