基于AdaBoost-Elman算法的锂离子电池荷电状态估计方法

谢旭，高晗,2，毕贵红，蒲娴怡，王凯

基于AdaBoost-Elman算法的锂离子电池荷电状态估计方法

谢旭1，高晗1,2，毕贵红1，蒲娴怡1，王凯1

（1. 昆明理工大学 电力工程学院，云南 昆明 650500；2. 云南电网有限责任公司 昆明供电局，云南 昆明 650011）

工作状态下的电池是一个动态的非线性系统，基于数据驱动的机器学习是锂离子电池估计建模的一类重要方法，其中基于神经网络的学习方法是典型代表。针对单一前馈型神经网络（如BP神经网络）预测过程中存在泛化能力低、局部极小化、预测精度低及动态性不足等问题，提出基于AdaBoost-Elman算法的锂离子电池估计方法。该方法充分利用了Elman神经网络的动态特性和AdaBoost算法提高弱预测器精度的特性，使组合后的强预测器具有较强的泛化能力、估计精度和动态特性。与BP神经网络和Elman神经网络的估计精度进行比较，AdaBoost-Elman神经网络的估计精度高、动态特性好，为锂离子电池估计提供了一种新的途径。

锂离子电池；估计；神经网络；集成学习

0 引言

电池值用于计量当前状态下电池剩余可用电量，不能直接使用测量手段获取，从而不满足实时监测的要求。工作状态下，电池系统时刻工作于非线性状态。目前电池管理系统针对的估计方法主要是通过监测电池组的电压、电流和温度等参数，借助经验查表法、电池机理模型等方法完成[1]。基于数据驱动的机器学习和统计方法，如神经网络、支持向量机等通过电池系统的输入和输出建立表征电池外部特性的非线性关系模型，精确再现了锂离子电池的非线性特征，同时考虑了外界温度、老化条件等环境干扰因素，模型具有较强适应性。神经网络是基于数据驱动的重要学习方法之一，具备自组织、自适应、自学习等功能，可以对复杂非线性对象建模和模拟，适合用来捕捉电池系统的非线性、动态性等特征[2]。

BP神经网络是神经网络中的代表算法，该算法的网络结构使用误差反向传播学习，在电池估计应用范围较广。文献[3]提出的方法解决了卡尔曼滤波法依赖精准电池模型的问题，运用神经网络优化EKF建立模型，同时修正EKF测量噪声协方差，经过仿真实验结果表明，本文中提出方法对于预测结果具有良好的收敛效果并具备一定的鲁棒性，应用价值较高。文献[4]通过将卡尔曼滤波器与神经网络算法融合组成估算方法，有效地降低了神经网络估算误差。文献[5]将遗传算法经过改进，结合到BP神经网络算法当中，构建了基于GA-BP的锂离子电池估计算法。经过仿真实验证实该方法有效地改善神经网络存在的最小值问题，同时保障一定的收敛速度。

由以上内容可知，随着机器学习技术的发展，BP神经网络在估计时仍存在算法上的缺点，如局部极小化、预测精度有限、过拟合等，而且前馈型神经网络缺乏记忆机制，动态适应性较差[6]。针对以上问题，本文使用Elman神经网络对锂离子电池进行估计，其拓扑结构比前馈型静态BP神经网络多了一个承接层作用延迟反馈，该反馈节点可以记录隐含层节点若干个时间延迟的输出值，能够表达输入与输出间的时间延迟，使网络结构具有记忆功能，方便系统动态过程的建模[7]。同时，基于传统神经网络精度不高、泛化性不好的问题，文中使用集成学习AdaBoost算法将若干个Elman预测器经过结合策略构成一个强预测器，进一步提高神经网络的估计精度[8]。本文提出的方法，充分利用Elman神经网络与AdaBoost算法的优势，使组合后的强预测器具备较好的估计精度和泛化能力，同时还具备了动态特性，经过NASA锂离子电池数据集实验验证，证明方法的有效性。

1 AdaBoost-Elman算法原理

1.1 Elman神经网络

BP神经网络是一个静态前馈型网络，在复杂情况下，该算法存在预测精度有限、局部极小化等问题，使误差在反向传播过程中无法准确纠错。本文使用Elman神经网络，通过在结构中构建承接层，作用储存、反馈隐含层神经元上一时刻的输出值，此举使Elman网络能够满足数据的动态反馈，是一种时延算方法。其结构如图1所示[2]。

Elman神经网络的数学模型可表示为：

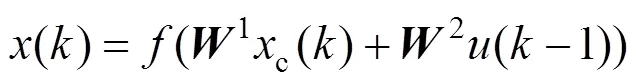
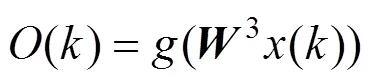
式中：1为承接层与隐含层的连接权矩阵；2为输入层与隐含层的连接权矩阵；3为隐含层与输出层的连接权矩阵；()为隐含层输出；c()为承接层输出；()为输出层输出；为自连接反馈增益因子；(–1)为输入；为长度。

Elman神经网络采用优化的梯度下降算法，该算法在保证训练速率的前提下也具备抑制局部极小值的能力。

1.2 自适应提升算法（AdaBoost）

本文使用的自适应提升（adaptive boosting，AdaBoost）是Boosting系列算法的一个代表，特点是提高任意给定学习算法精度，每一个个体预测器之间具有依赖性，整个学习过程通过对前一个错分的数据提高权重来提升性能，也就是说下一个预测器的构造和上一个预测器有关，实现方法如图2所示。

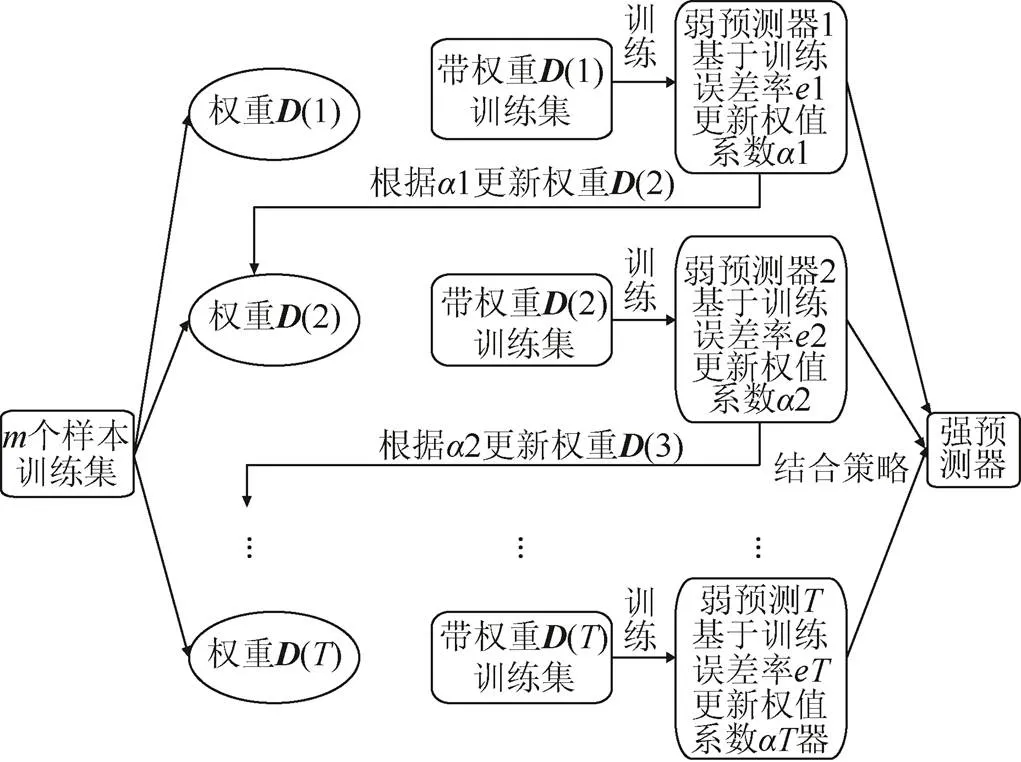
图2 AdaBoost算法

由图2可知，首先，令初始状态全部训练样本权重相等，基于此，权重分布通过训练得到一个弱预测器；然后根据本次训练误差调整权重，将误差超过阈值的样本权重提高，使用调整后的权重训练第二个预测器。依照以上步骤开始次迭代，在第（=1,2,···,，其中，为迭代次数）次迭代中，样本权重由第–1次迭代的结果而定。经过以上次循环，得到个弱预测器，将得到的所有弱预测器按照一定的权重整合，得到最终的强预测器。

为了对AdaBoost算法做进一步理论分析，使用数学化的语言描述一下AdaBoost算法的过程[8]。

步骤1 初始化的权值分布为：

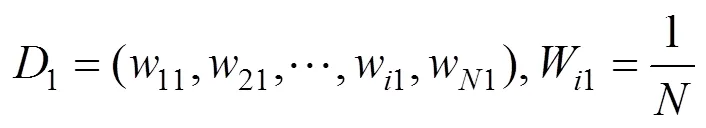
步骤2 执行轮学习，第（=1,2,···,）轮学习过程如下：

（1）在权值分布D的训练集上训练模型M()。

（2）评估M()在训练集上的错误率e：

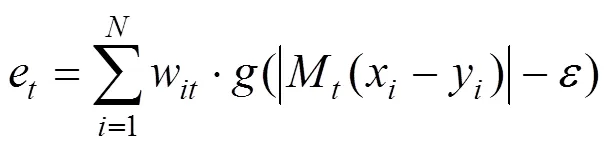
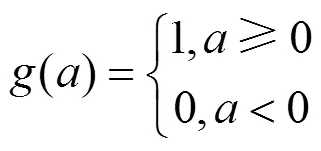
式中：为预先设置的阈值，样本x的预测值与真实值的误差小于，则x被正确预测；否则，x被错误预测。

（3）根据错误率e计算M()的权重：

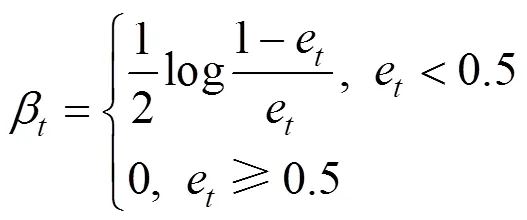
M()的错误率e大于0.5，舍弃该模型。

（4）更新训练集上的权值分布：

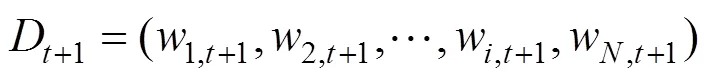
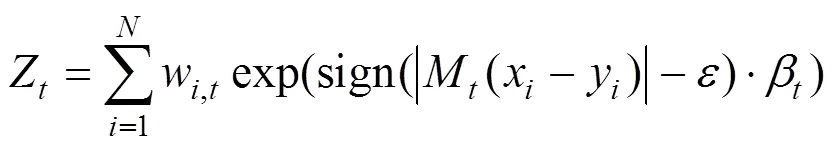
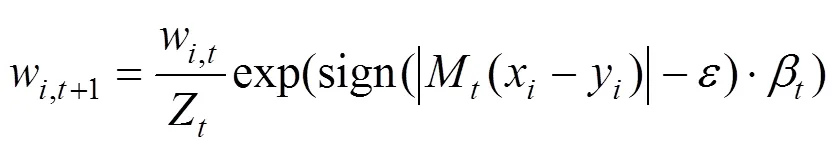
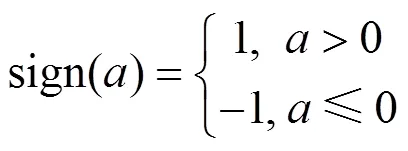
式中：Z为标准化因子，若x被正确预测，则减小x对应的权重；否则，增大x对应的权重。

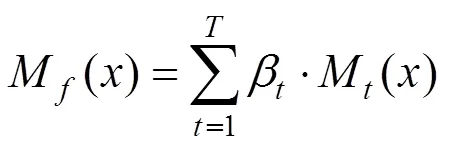
AdaBoost算法在应用上取得良好的效果，但过拟合的问题依然存在。比如，在上述算法中，样本训练集重复使用在构造模型和评估错误率这两项运算过程中，导致构建好的模型展现较好的预测性能仅仅针对训练集数据，然而通过测试集验证展现的结果不理想，泛化能力差。本文针对以上问题，在使用算法构建模型时引入一个独立评估数据集用于评估模型的错误率。该独立评估数据集中使用的样本不同于训练集中采用的样本数据[9]。

2 基于AdaBoost-Elman算法的SOC估计算法

2.1 算法估计流程

Elman神经网络具有收敛快、不易陷入局部极小值的优点，而AdaBoost算法具备串行集成学习的优点，通过弱预测器的相互依赖关系并按照一定的权重组合成为强预测器。本文结合两种算法提出了基于AdaBoost-Elman的估计算法，其核心思想是利用集成学习理论将数据层融合问题转化为决策层融合问题，估计流程如图3所示。

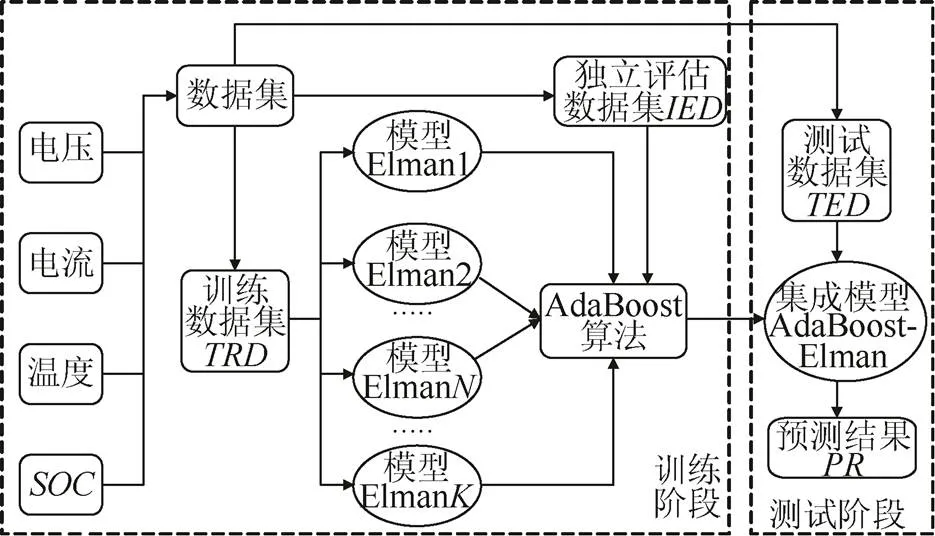
图3 基于AdaBoost-Elman算法的SOC估计流程图

根据图3，AdaBoost-Elman估计算法分为以下两个阶段。

训练阶段：

输出：集成模型AdaBoost-Elman。

步骤1 将电压、电流、温度和值构成训练数据集，将训练数据集使用初始权重训练得到Elman1预测器，计算该预测器的学习误差率，并依据误差率更新训练样本的权重，提升Elman1中学习误差率高的样本点权重。

步骤2 基于调整权重后的训练集来训练Elman2，重复上述步骤操作，直到Elman预测器数目达到事先给定的数目。

步骤3 结合独立评估数据集，利用AdaBoost算法对个Elman模型进行集成，得到集成的Elman模型，表示为：

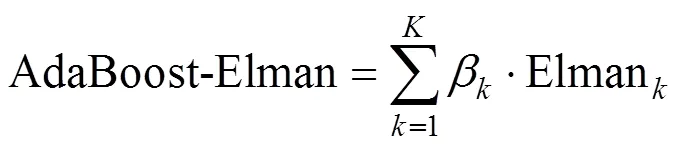
测试阶段：

输入：测试数据集；集成的Elman模型AdaBoost-Elman。

输出：预测结果PR。

步骤1 分别用AdaBoost-Elman中的每个Elman模型对测试数据集进行预测，预测结果依次表示为1,2,···,Y。

步骤2 按照如下公式计算最终预测结果：

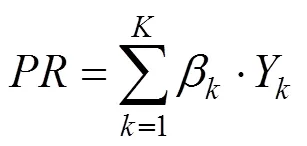
2.2 算法评价指标

为了评价建立的估计模型，将预测数据和实际数据做对比，本文选取3个统计量：平均绝对误差（mean absolute error，MAE）、平均绝对值百分比误差（mean absolute percentage error，MAPE）和均方根误差（root mean square error，RMSE）。各类误差具体计算表达式如下：

平均绝对误差（MAE）：

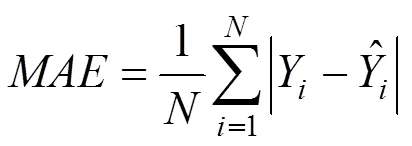
平均绝对值百分比误差（MAPE）：

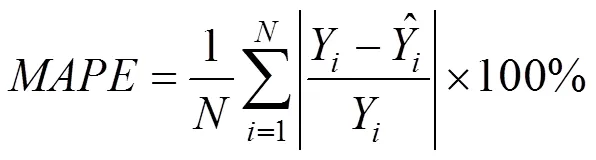
均方根误差（RMSE），计算公式为：

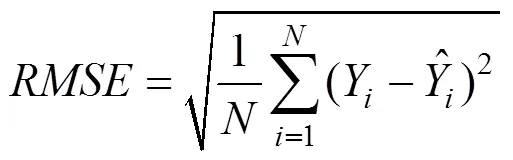
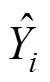
3 实验仿真与结果分析

3.1 实验数据的预处理

本文实验选择NASA PCoE研究中心的锂电池放电实验数据，从中提取部分电池组数据用于实验。根据上文仿真实验步骤，选用电池组的电压、电流、温度作为系统模型的输入值，选用值作为系统模型的输出值[10]。实验条件如表1所示。

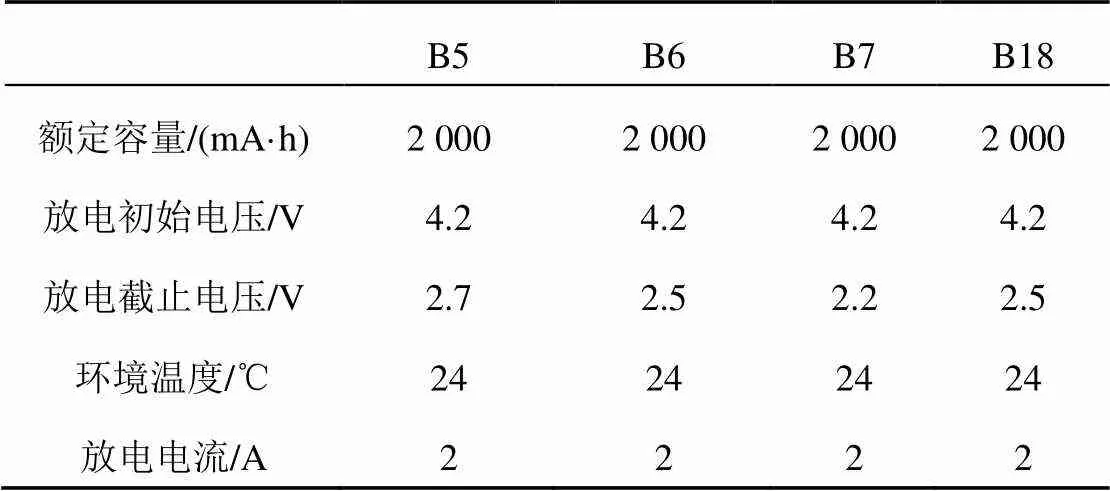
表1 锂离子电池实验条件

由于不能直接获得，本文使用安时积分法[11-12]计算电池组的值，已知该实验放电过程在实验室条件下进行，测量的电流足够精确且的初始值明确，因此根据下式计算电池的值[13]：

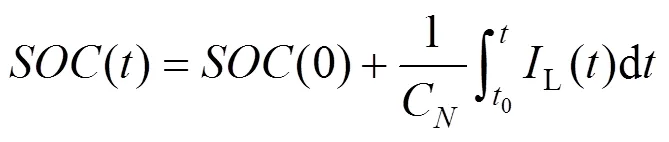
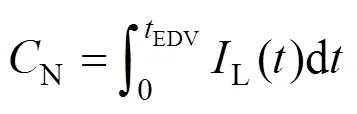
式中：()为时刻的值；(0)为0时刻的值；N为额定容量（A·h）；L()为放电电流；EDV为当放电电压达到截止电压时的放电时间。

图4所示为随放电时间的曲线图。随着放电过程的进行，值从1下降至0.358 9，下降速率接近于线性，证实了放电时间与有近似线性关系[14]。

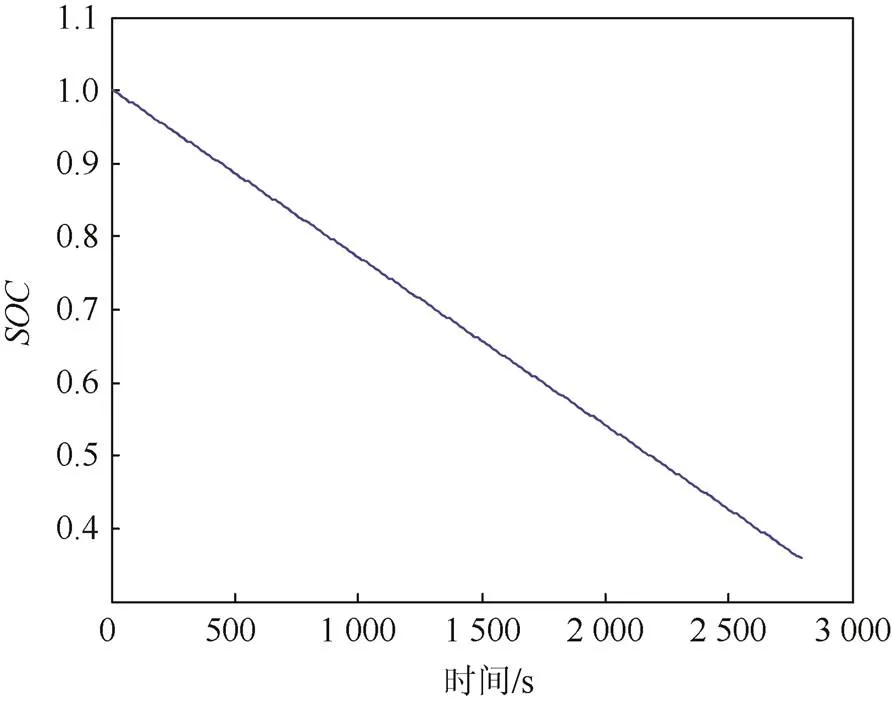
图4 SOC随放电时间的曲线图

3.2 样本数据归一化处理

考虑到神经网络运算特性，将取值较大的数据直接输入网络中的操作容易导致网络无法收敛，运算量也极其庞大。为了减缓神经网络的学习压力，本文将输入数据做了归一化处理[15]。本文数据归一化采用离差标准化，对原始数据做变化，将其映射到[0,1]范围内，公式如下：

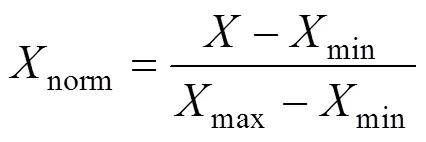
式中：norm为归一化后的值；为归一化前的样本数据值；min、max为样本数据中最小值和最大值。

3.3 实验结果分析

本文以B5、B6、B7、B18电池组为例，对提出的预测方法进行分析和验证，设置弱预测器Elman神经网络的输入层节点个数为3个，分别是电池的电压、电流和温度数据，隐含层的节点个数为7个，输出层的节点个数为1个，是电池的预测值，弱预测器的个数取10个。

（1）B5电池估计结果

B5数据集中，选用第1组、第21组、第41组、第61组数据作为模型的训练数据集；选用第11组、第31组、第51组、第71组数据作为模型的独立评估数据集；选用第81组数据作为模型的测试数据集，根据实验步骤得到的估计结果及平均绝对值百分比误差如图5和图6所示。

图5为估计结果对比图。从图5中可以看出，AdaBoost-Elman神经网络估计值与真实值拟合度最高。

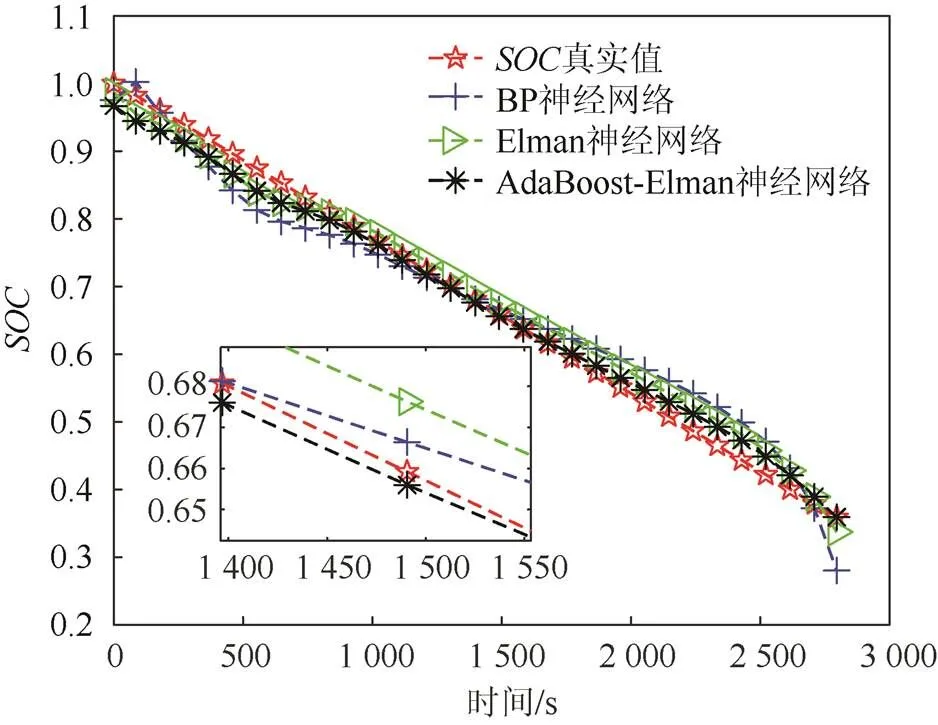
图5 B5电池SOC估计结果对比图

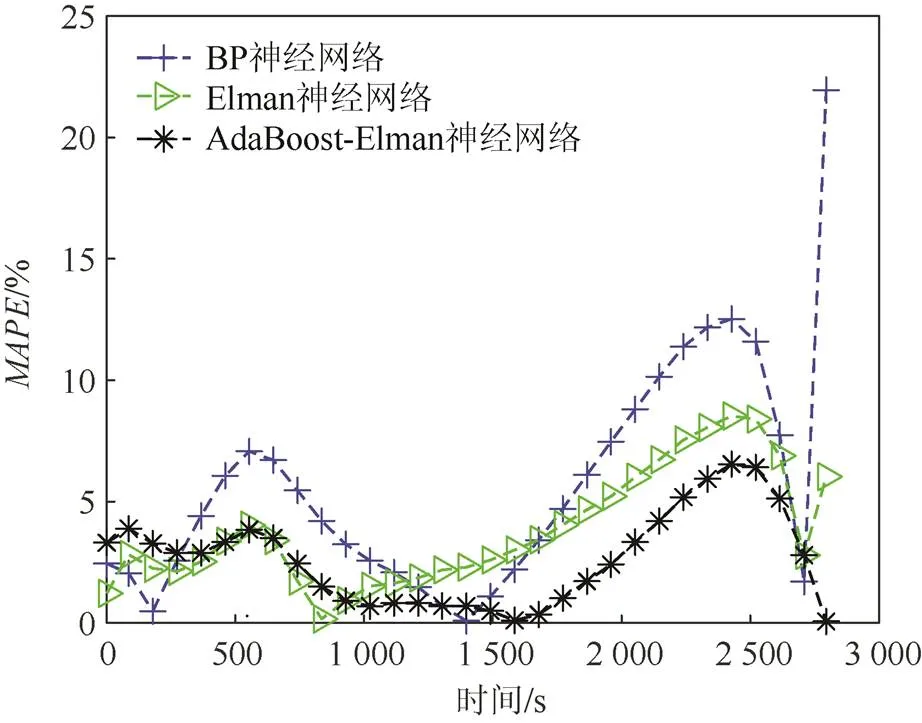
图6 B5电池平均绝对值百分比误差曲线

图6为3种估计方法的平均绝对值百分比误差曲线。从图6中可以看出，BP和Elman随着输入向量的变化，估计误差处于较大的范围，AdaBoost-Elman神经网络可以确保误差在一定范围内，平均绝对值百分比误差最大不超过6.7%。

表2所示为3种预测方法的3种误差，从表2可知，BP神经网络、Elman神经网络和AdaBoost- Elman神经网络的平均绝对值百分比误差分别为5.386 4%、3.783 8%和2.662 2%，均方根误差分别为0.037 4、0.024 9和0.020 7。

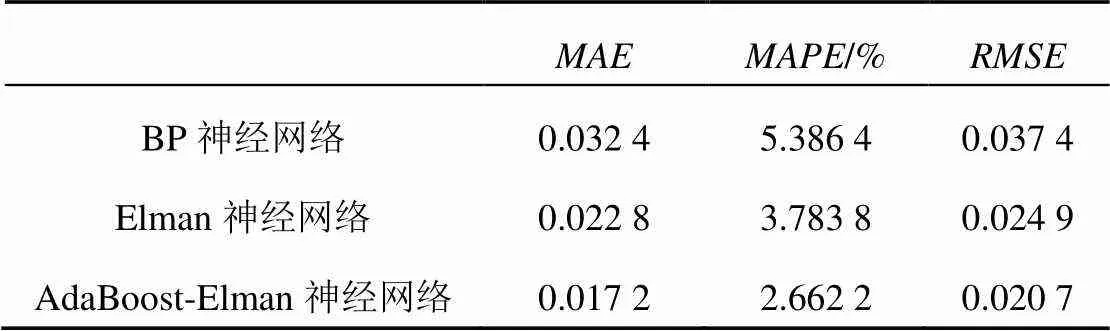
表2 B5电池预测精度对比

（2）B6电池估计结果

B6数据集中，选用第1组、第21组、第41组、第61组数据作为模型的训练数据集；选用第11组、第31组、第51组、第71组数据作为模型的独立评估数据集；选用第81组数据作为模型的测试数据集，得到的估计结果及平均绝对值百分比误差如图7和图8所示。

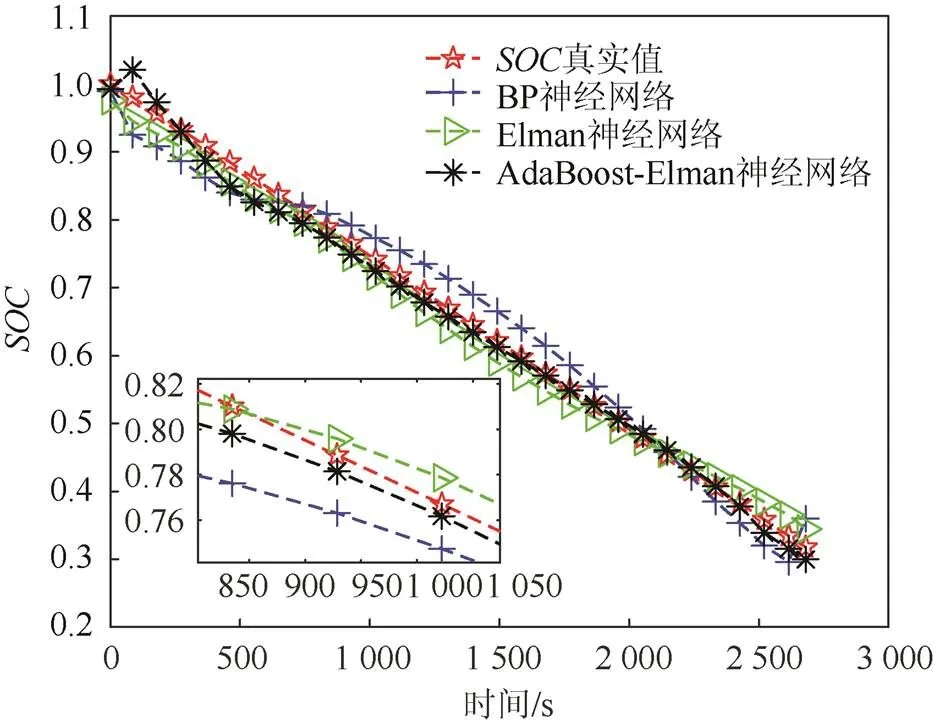
图7 B6电池SOC估计结果对比图

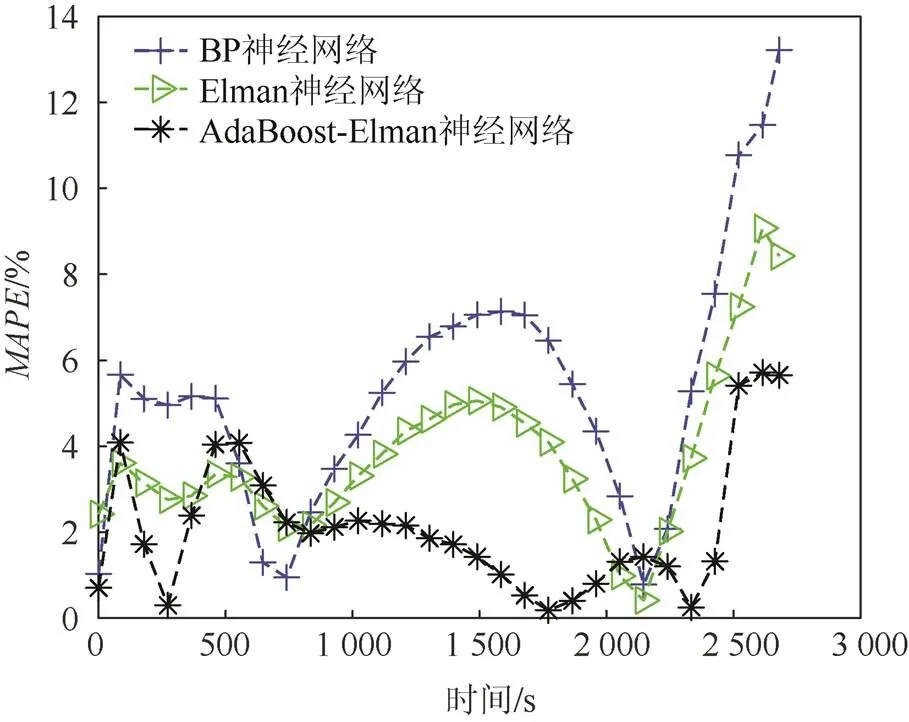
图8 B6电池平均绝对值百分比误差曲线

表3所示为3种预测方法的3种误差，从表3可知，BP神经网络、Elman神经网络和AdaBoost- Elman神经网络的平均绝对值百分比误差分别为5.096 2%、3.699 2%和2.098 3%，均方根误差分别为0.035 2、0.024 6和0.018 4。

表3 B6电池预测精度对比

（3）B7电池估计结果

B7数据集中，选用第5组、第25组、第45组、第65组数据作为模型的训练数据集；选用第15组、第35组、第55组、第75组数据作为模型的独立评估数据集；选用第85组数据作为模型的测试数据集，得到的估计结果及平均绝对值百分比误差如图9和图10所示。

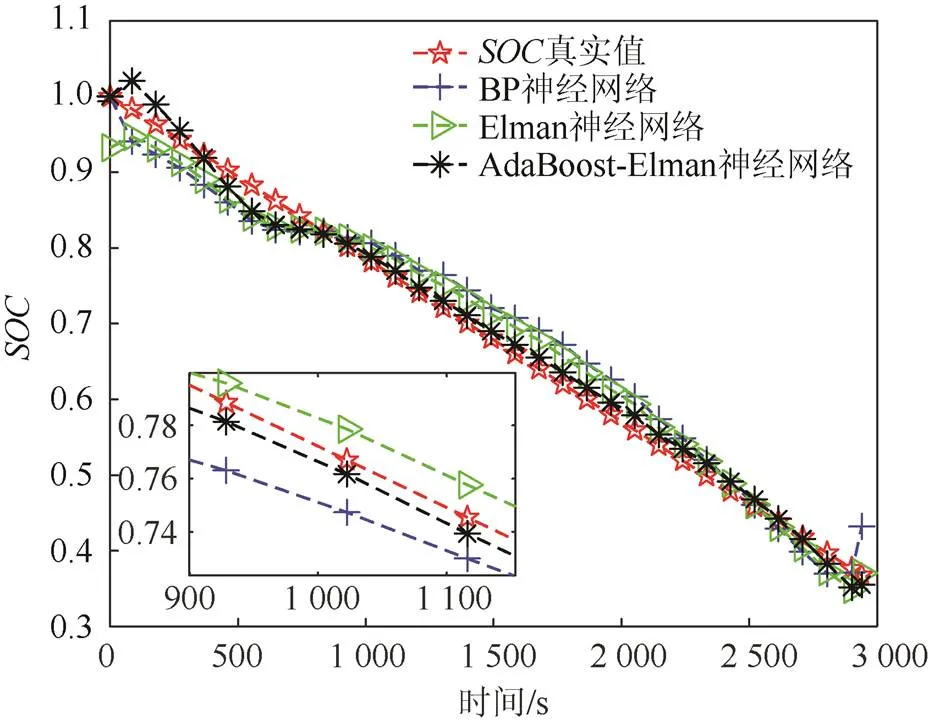
图9 B7电池SOC估计结果对比图

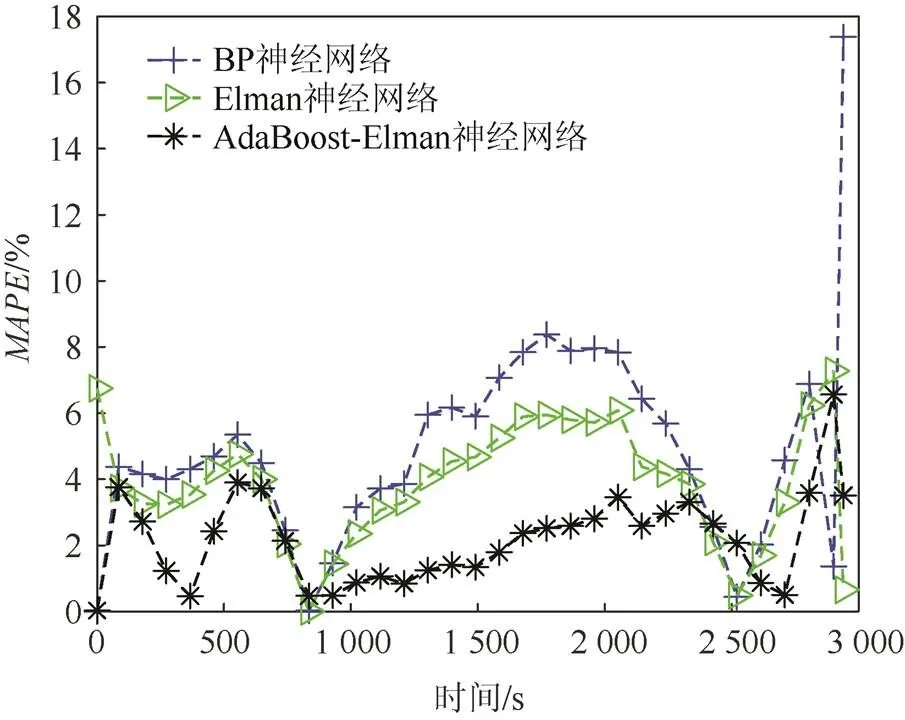
图10 B7电池平均绝对值百分比误差曲线

表4所示为3种预测方法的3种误差，从表4可知，BP神经网络、Elman神经网络和AdaBoost- Elman神经网络的平均绝对值百分比误差分别为4.775 9%、3.872 5%和2.171 0%，均方根误差分别为0.034 9、0.028 4和0.017 1。

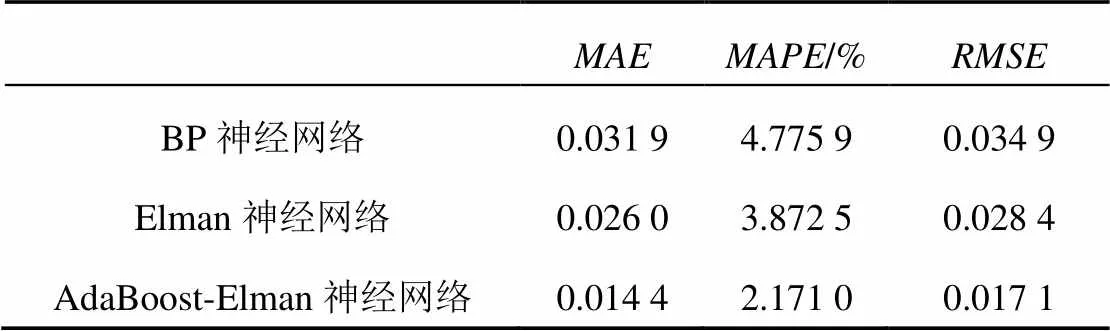
表4 B7电池预测精度对比

（4）B18电池估计结果

B18数据集中，选用第9组、第29组、第49组、第69组数据作为模型的训练数据集；选用第19组、第39组、第59组、第79组数据作为模型的独立评估数据集；选用第89组数据作为模型的测试数据集，得到的估计结果及平均绝对值百分比误差如图11和图12所示。

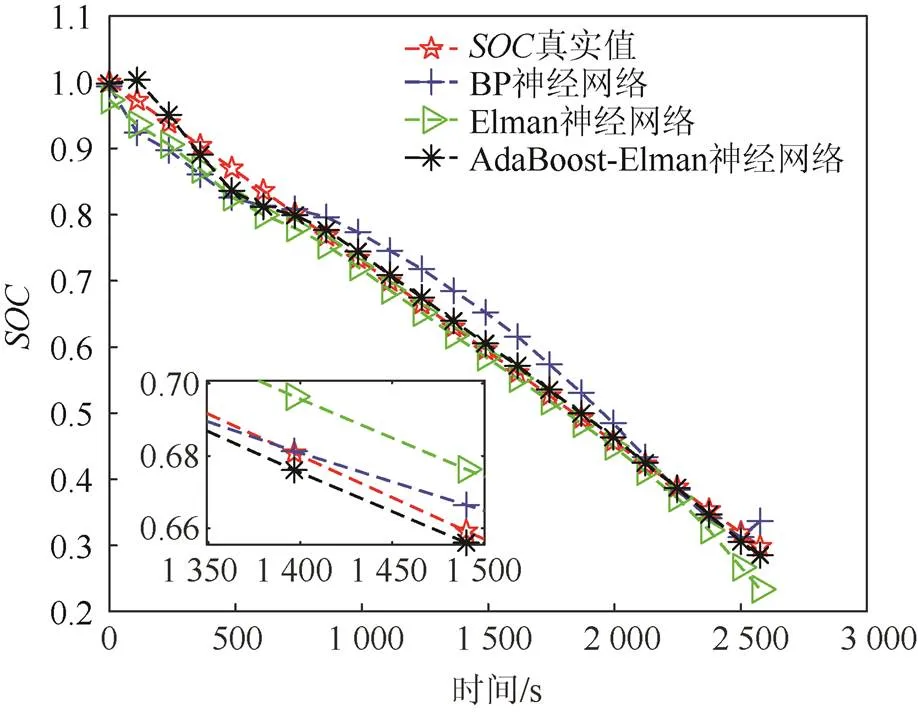
图11 B18电池SOC估计结果对比图

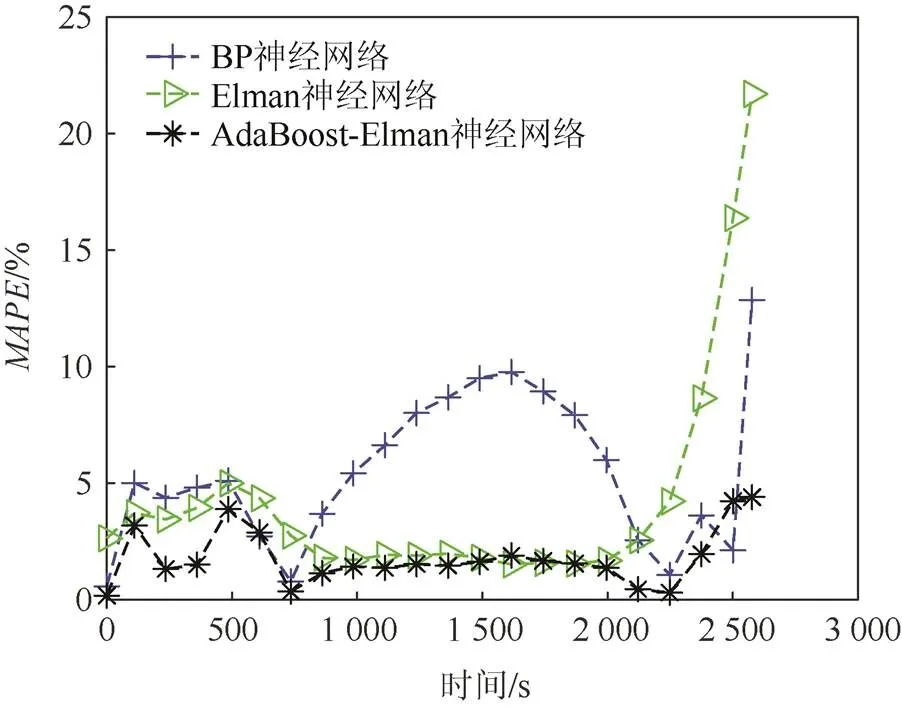
图12 B18电池平均绝对值百分比误差曲线

表5所示为3种预测方法的3种误差，从表5可知，BP神经网络、Elman神经网络和AdaBoost- Elman神经网络的平均绝对值百分比误差分别为5.407 9%、3.768 0%和1.803 8%，均方根误差分别为0.039 1、0.026 0和0.014 9。

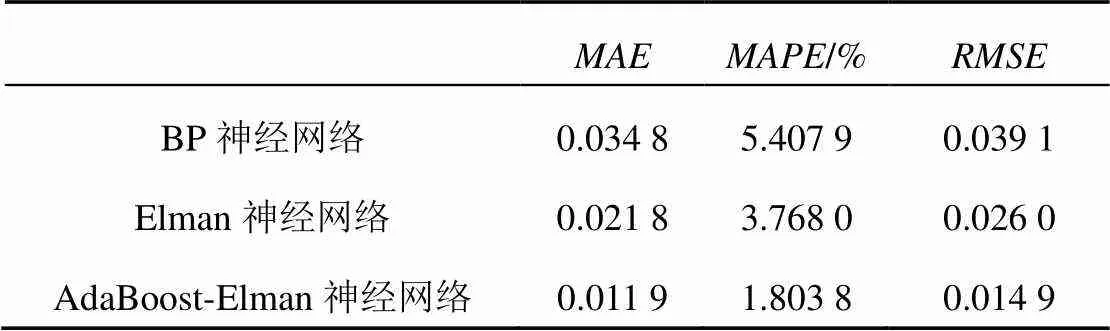
表5 B18电池预测精度对比

从以上各表数据可知，AdaBoost-Elman相比BP神经网络的估计精度提升明显，与Elman神经网络相比估计精度也有提升，说明基于AdaBoost- Elman算法的估计具有良好的估计效果。

图13以B5电池组为例，表示B5电池组Adaboost-Elman神经网络与Elman神经网络仿真误差迭代曲线图，其中横坐标为迭代次数，纵坐标为平均绝对误差。从图13可以看出，Adaboost-Elman神经网络的迭代次数为11左右，基本达到网络设置精度要求，而Elman神经网络要在22步迭代时才达到，由此可见，Adaboost-Elman神经网络表现出更加快速的收敛速度。

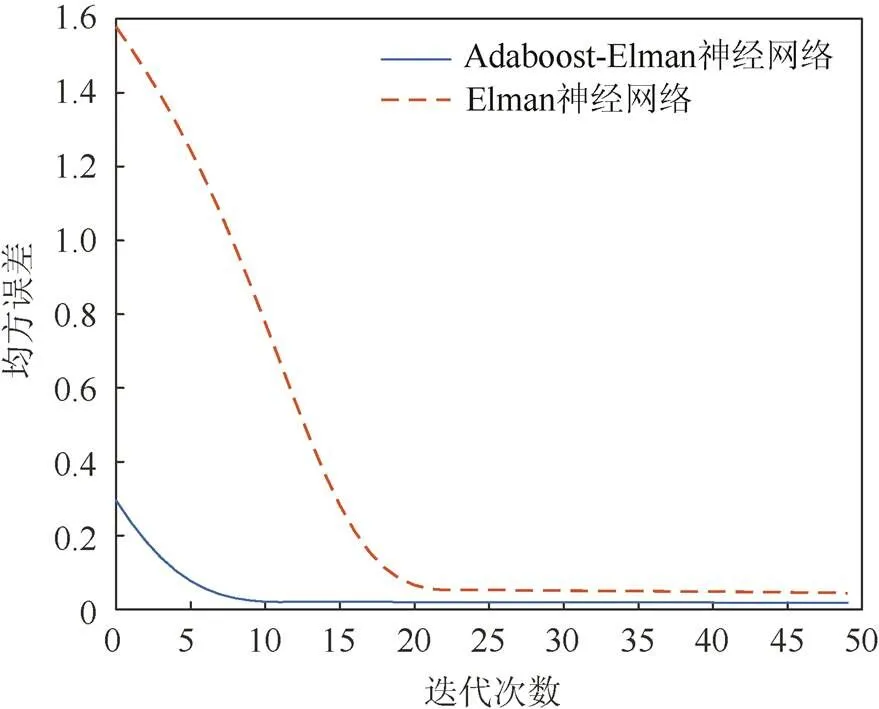
图13 B5电池组仿真误差迭代曲线

4 结论

本文采用数据驱动的方法对锂离子电池进行估计，针对单一前馈型神经网络（如BP神经网络）预测过程中存在的预测精度低、动态适应性较差等问题，采用具有记忆功能和动态信息处理能力的Elman神经网络，对锂离子电池估计进行建模。将Elman神经网络作为弱预测器，利用AdaBoost算法融合若干Elman神经网络组成一个强预测器对锂离子电池估计。以B5电池为例进行说明，BP神经网络的为5.386 4%，Elman神经网络的为3.783 8%，AdaBoost- Elman神经网络的为2.662 2%，验证了Elman神经网络的动态特性和AdaBoost算法提高弱预测器精度的特性，组合后的强预测器具有较强的泛化能力，相较于Elman预测器，收敛速度明显提升，证明了基于AdaBoost-Elman算法的锂离子电池估计的有效性。

[1] LI JIANHUA, LIU MINGSHNEG. State-of-charge estimation of lithium-ion batteries using composite multi-dimensional features and a neural network[J]. IET Power Electronics, 2019, 12(6): 1470-1478.

[2] 王小川. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013. WANG XIAOCHUAN. MATLAB neural network analysis of 43 cases[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2013(in Chinese).

[3] 商云龙, 张承慧, 崔纳新, 等. 基于模糊神经网络优化扩展卡尔曼滤波的锂离子电池荷电状态估计[J]. 控制理论与应用, 2016, 33(2): 212-220. SHANG YUNLONG, ZHANG CHENGHUI, CUI NAXIN, et al.State of charge estimation for lithium-ion batteries based on extended Kalman filter optimized by fuzzy neural network[J]. Control Theory & Applications, 2016, 33(2): 212-220(in Chinese).

[4] 刘晓悦, 杜晓. 基于神经网络与UKF结合的锂离子电池组SOC估算方法[J]. 现代电子技术, 2018, 41(2): 120-123. LIU XIAOYUE, DU XIAO.Method for lithium-ion battery pack SOC estimation based on combination of neural network and UKF[J]. Modern Electronics Technique, 2018, 41(2): 120-123(in Chinese).

[5] 于仲安, 卢健, 王先敏. 基于GA-BP神经网络的锂离子电池SOC估计[J]. 电源技术, 2020, 44(3): 337-340. YU ZHONG’AN, LU JIAN, WANG XIANMIN. SOC estimation of Li-ion battery based on GA-BP neural network[J]. Chinese Journal of Power Sources, 2020, 44(3): 337-340(in Chinese).

[6] 冷雨泉. 机器学习入门到实战MATLAB实践应用[M].北京: 清华大学出版社, 2018.

LENG YUQUAN. Introduction of machine learning to practical application of MATLAB[D]. Beijing:Tsinghua University Press, 2018(in Chinese).

[7] 游皓麟. R语言预测实战[M]. 北京: 电子工业出版社, 2017.

YOU HAOLIN. R language prediction practice[M]. Beijing: Publishing House of Electronics Industry, 2017(in Chinese).

[8] 周润景. 模式识别与人工智能[M]. 北京: 清华大学出版社, 2018.

ZHOU RUNJING. Pattern recognition and artificial intelligence[M]. Beijing:Tsinghua University Press, 2018(in Chinese).

[9] 田明光, 翟旭, 江颖洁, 等. 基于K均值聚类及高斯过程回归集成的铅酸电池荷电状态预测[J]. 软件, 2018, 39(1): 132-137. TIAN MINGGUANG, ZHAI XU, JIANG YINGJIE, et al. Prediction for state of charge of lead-acid batteries by K-means cluster with ensemble gaussian process regression[J]. Computer Engineering & Software, 2018, 39(1): 132-137(in Chinese).

[10] 韦振汉, 宋树祥, 夏海英. 基于随机森林的锂离子电池荷电状态估算[J]. 广西师范大学学报(自然科学版), 2018, 36(4): 27-33. WEI ZHENHAN, SONG SHUXIANG, XIA HAIYING. State-of-charge estimation using random forest for lithium ion battery[J]. Journal of Guangxi Normal University(Natural Science Edition), 2018, 36(4): 27-33(in Chinese).

[11] 明彤彤, 王凯, 田冬冬, 等. 基于LSTM神经网络的锂离子电池荷电状态估算[J]. 广东电力, 2020, 33(3): 26-33. MING TONGTONG, WANG KAI, TIAN DONGDONG, et al. Estimation on state of charge of lithium battery based on LSTM neural network[J]. Guangdong Electric Power, 2020, 33(3): 26-33(in Chinese).

[12] 付浪, 杜明星, 刘斌, 等. 基于开路电压法与卡尔曼滤波法相结合的锂离子电池SOC估算[J]. 天津理工大学学报, 2015, 31(6): 9-13. FU LANG, DU MINGXING, LIU BIN, et al. Estimation of lithium-ion battery SOC based on combination of open-circuit voltage and Kalman filter[J]. Journal of Tianjin University of Technology, 2015, 31(6): 9-13(in Chinese).

[13] 赵天意, 彭喜元, 彭宇, 等. 改进卡尔曼滤波的融合型锂离子电池SOC估计方法[J]. 仪器仪表学报, 2016, 37(7): 1441-1448. ZHAO TIANYI, PENG XIYUAN, PENG YU, et al. Lithium-ion battery SOC estimation method with fusion improved Kalman filter algorithm[J]. Chinese Journal of Scientific Instrument, 2016, 37(7): 1441-1448(in Chinese).

[14] 季迎旭, 杜海江, 孙航. 蓄电池SOC估算方法综述[J]. 电测与仪表, 2014, 51(4): 18-22. JI YINGXU, DU HAIJIANG, SUN HANG.A survey of state of charge estimation methods[J]. Electrical Measurement & Instrumentation, 2014, 51(4): 18-22(in Chinese).

[15] 吴海东, 任晓明, 那伟, 等. 改进安时法结合神经网络估算锂离子电池SOC[J]. 电池, 2016, 46(1): 16-19. WU HAIDONG, REN XIAOMING, NA WEI, et al. Estimating SOC of Li-ion battery by improved AH combined with neural network[J]. Battery Bimonthly, 2016, 46(1): 16-19(in Chinese).

State-of-charge Estimation Method for Lithium-ion Batteries Based on AdaBoost-Elman Algorithm

XIE Xu1, GAO Han1,2, BI Guihong1, PU Xianyi1, WANG Kai1

(1. Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming 650500, China; 2. Kunming Electric Power Supply Bureau, Yunnan Power Grid Co., Ltd., Kunming 650011, China)

Battery under working condition is a dynamic nonlinear system. Data-driven machine learning method is an important method for modelingestimation of lithium-ion batteries, and learning method based on neural network is a typical representative. Aiming at solving the problems of low generalization ability, local minimization, low prediction accuracy and insufficient dynamics in the prediction process of single feedforward neural network (such as BP neural network), this paper proposes aestimation method of lithium-ion batteries based on Adaboost-Elman algorithm. This method makes full use of the dynamic characteristics of Elman neural network and AdaBoost algorithm to improve the accuracy of weak predictors, so that the combined strong predictors have strong generalization ability, estimation accuracy and dynamic characteristics. Compared with BP neural network and Elman neural network, Adaboost-Elman neural network has higher estimation accuracy and better dynamic characteristics, which provides a new approach forestimation of lithium-ion batteries.

lithium-ion batteries;estimation; neural network; integrated learning

10.3969/j.ISSN.1672-0792.2021.02.007

TM912

A

1672-0792(2021)02-0048-09

2020-11-12

谢 旭（1996—），男，硕士研究生，研究方向为人工智能算法在电力系统中的应用；

高 晗（1995—），男，硕士研究生，研究方向为锂离子电池组状态传感与监测；

毕贵红（1968—），男，教授，研究方向为信号处理与模式识别；

蒲娴怡（1995—），女，硕士研究生，研究方向为数据分析及功率预测；

王 凯（1993—），男，硕士研究生，研究方向为风电风速和功率预测。

毕贵红