基于WPHM模型和模糊综合评估的变压器健康状态评价

郑文光，谢红玲，李燕青，王爱军，王冠，张潇文

基于WPHM模型和模糊综合评估的变压器健康状态评价

郑文光1，谢红玲2，李燕青2，王爱军3，王冠3，张潇文4

（1. 大唐国际发电股份有限公司陡河发电厂，河北 唐山 063000；2. 华北电力大学电气与电子工程学院，河北 保定 071003；3. 唐山市气象局，河北 唐山 063000；4. 唐山师范学院资源管理系，河北 唐山 063000）

针对当前变压器状态评价模糊性大、评估指标片面、指导性不强的问题，提出了一种基于WPHM模型和模糊综合评估的变压器健康状态评价方法。首先从电气、油化、油气和物理4种性质出发建立两级状态指标体系，提高了评估全面性和信息采集效率；然后以二级指标为基础构建WPHM模型来全面分析一级指标风险，并采用威布尔概率图法和极大似然估计法估算参数，提高了参量的计算速度；最后结合最优可用度理论构建隶属度函数，从而得到变压器风险度与状态的模糊关系，在变权重的作用下得出变压器整体的风险水平。经过实例分析验证，该评价方法客观准确、便捷有效，在工程中具有良好的实用性，能够为变压器的检修提供指导与帮助。

变压器；WPHM模型；模糊综合评估；健康状态评价

0 引言

变压器作为电站与电网联系的枢纽，其可靠运行同时关系到发电厂和电网的安全稳定，所以对变压器的维护与检修至关重要[1-2]。近些年来，变压器传统检修方式极易造成“过修”和“欠修”的问题日益突显[3]，为解决这一问题，状态检修技术逐步兴起，而状态检修能否取得预期效果的关键在于状态评估的结果，因此状态评估的方式方法始终是设备运行维护人员最关心的热门话题之一。

国内外诸多学者针对变压器状态评估方法和模型进行了理论和应用上的研究。文献[4-5]采用了一些性能比较优异的智能算法对变压器的状态进行评价，并通过实验证实了方法的有效性，但由于这些方法仅根据油类指标进行评估，缺少对变压器油以外指标的分析，造成了评估结果具有一定的片面性。文献[6]以油浸式变压器为研究对象，从局部评估和整体评估两个角度分别建立了有针对性的状态评估模型，但由于部分指标只能通过实验室条件下来获取，导致模型在现场推广应用方面可行性较差。文献[7-8]对变压器状态指标信息进行了全面研究，制定了较为合理有效的状态指标信息集，但由于在模型建立过程中按固定权重分析指标，忽略了权重与各指标量之间的实时关联性，在一定程度上影响了评价结果。文献[9-10]立足于各状态指标之间的模糊性，从定性和定量相结合的角度建立评价模型，但由于在指标评价过程中采用的是专家打分法，造成了评价结果的客观性不强。

针对上述情况，本文提出了一种基于WPHM模型和模糊综合评估的变压器健康状态评价方法。首先，根据指标性质建立两级状态指标体系；然后，通过威布尔概率图法和极大似然估计法构造的WPHM模型来全面分析一级指标风险度；最后，根据最优可用度理论构建岭形隶属度函数，从而得到一级指标的模糊关系矩阵，再引入变权重评价出变压器整体的状态等级。经过实例分析验证了该方法在实际工程中具有良好的效果，能够有效应用于变压器的状态检修工作。

1 变压器状态指标体系

1.1 状态指标体系的建立

建立合理有效的状态评估指标体系是进行状态评估的基础，变压器属于大型电力设备，其结构复杂，部件众多[11]，传统的状态指标体系很难包含变压器的所有指标信息，极易造成评估结果缺乏全面性和准确性，也不利于信息收集和数据监测。因此本文按照指标的性质建立评价体系，具有良好的统计学意义，能够有效解决上述问题。

本文针对SFSZ-34000/220型油浸式变压器，从电气、油化、油气、物理4种性质出发，根据文献[12-13]选择指标量，构建如表1所示的变压器两级状态指标评价体系。

表1 状态指标体系

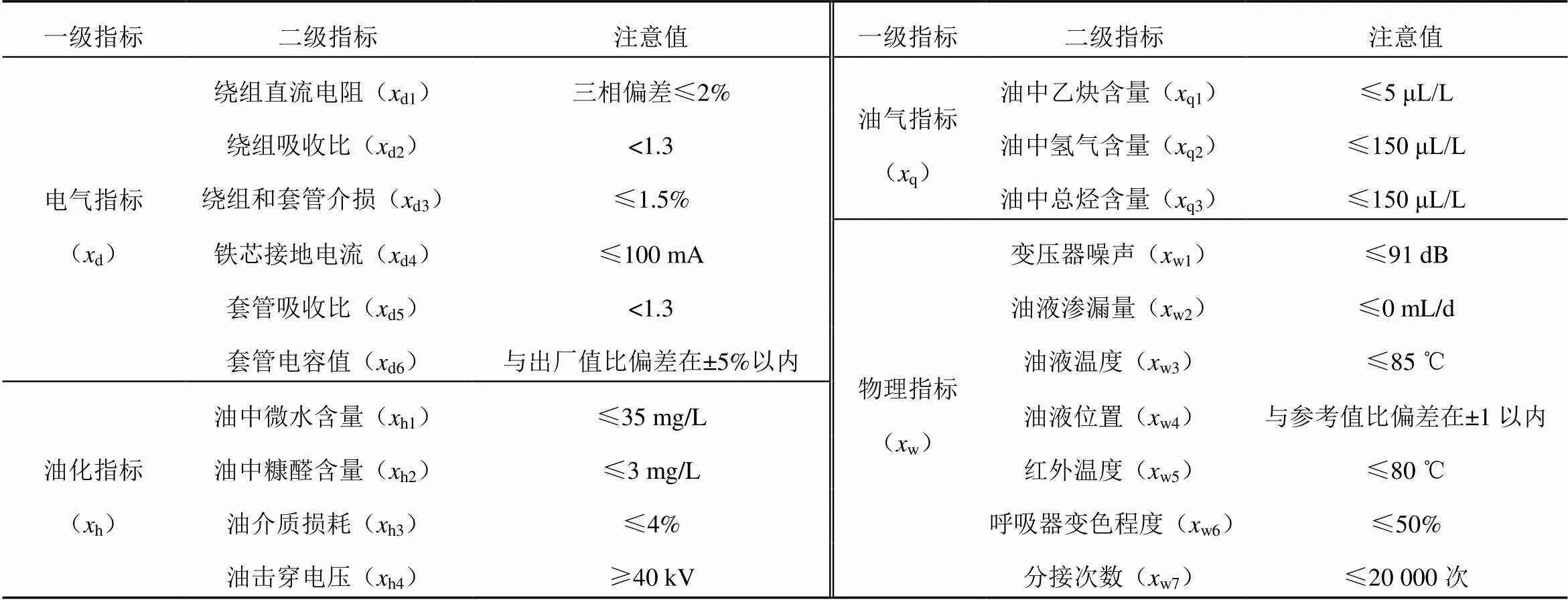
Tab.1 Condition index system

1.2 指标量的标准化处理

由于各二级指标的量纲和数量级各不相同，若直接运用监测得到的数据进行运行状态评估，则会造成评估结果的不准确[14]，因此本文采用离差标准化法对各二级指标的监测值进行标准化处理[15]，使之成为[0,1]区间内的标准化数据进行状态估计。

变压器的二级指标可分为越大越优秀型和越小越优秀型两种，其标准化公式分别如式（1）和式（2）所示。

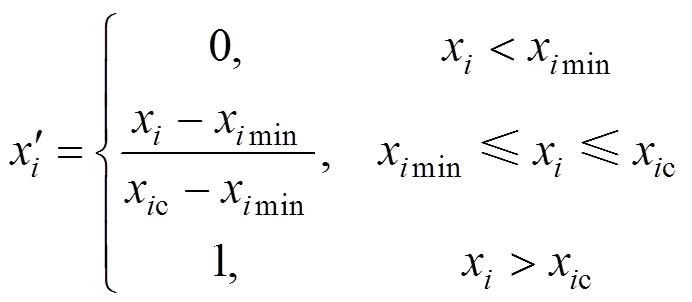
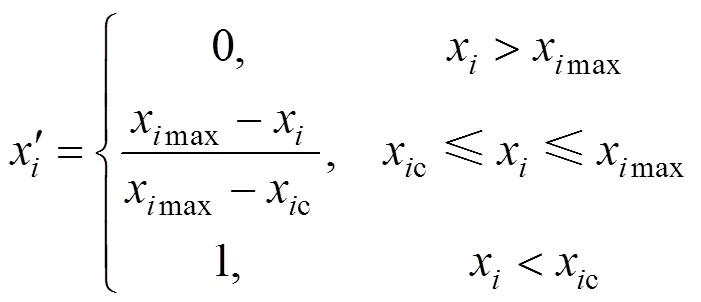
2 变压器状态评估模型

2.1 WPHM风险度模型

2.1.1 风险度模型的建立

若为随机变量，设备的风险度()是指设备在当前时刻处于正常情况下，运行时间后下一刻发生故障或失效的条件概率[16]，如式（3）所示。

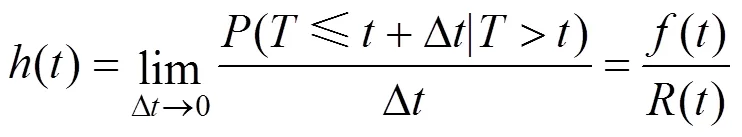
式中：()为概率密度函数。

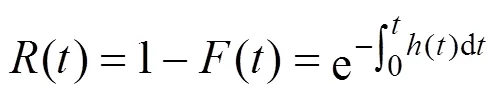
式中：()为可靠度函数；()为概率分布函数。

威布尔比例失效模型（Weibull proportional hazards model，WPHM）是一种寿命数据服从威布尔分布的设备故障风险度评估模型[17]，该模型能够综合反映自然老化程度和实时状态变化对设备风险度造成的影响。因此，在医学和工程的可靠性分析上有十分广泛的应用。本文对变压器各一级指标建立WPHM模型如式（5）所示。

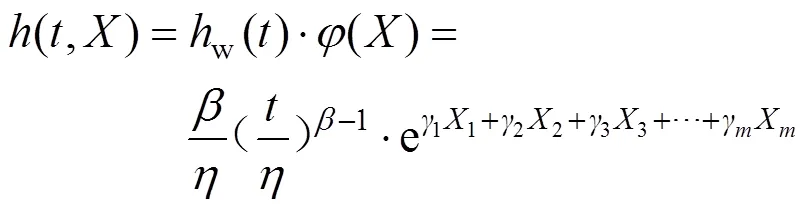
式中：w()为威布尔基本失效函数；()为状态指标函数；为设备的实际运行时间；为形状参数；为尺度参数；表示在时刻设备对应的状态指标量；(=1,2,···,)为状态指标x(=1,2,···,)的回归系数。

2.1.2 风险度模型的参数估计

构建WPHM模型的关键在于、和这3个参数的确定。为了保证在结果准确性的前提下缩短计算时间，提高运算效率，本文选用威布尔概率图法和极大似然估计法对模型中的参数进行估计。

令=η，代入威布尔分布函数w()可得到式（6）。

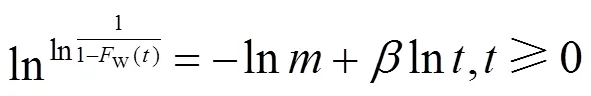
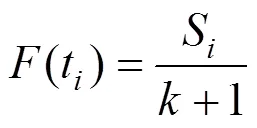
表2 由各一级指标引起的变压器部分历史故障时间统计表

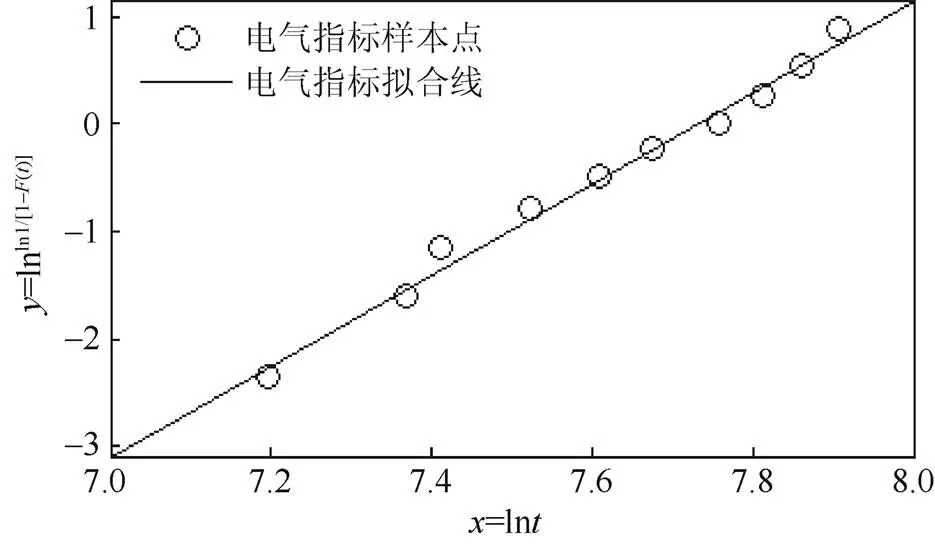
分别在时刻t(=1,2,3,···,10)对每个二级指标采集状态监测值，经标准化处理后得到如表3所示的二级指标状态量的标准化值(t)，构造极大似然估计样本。在式（7）所示的WPHM风险度模型的概率密度函数基础上，构建似然函数得到式（8）。

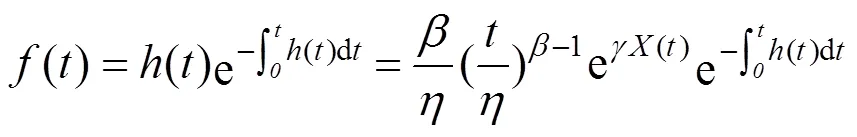
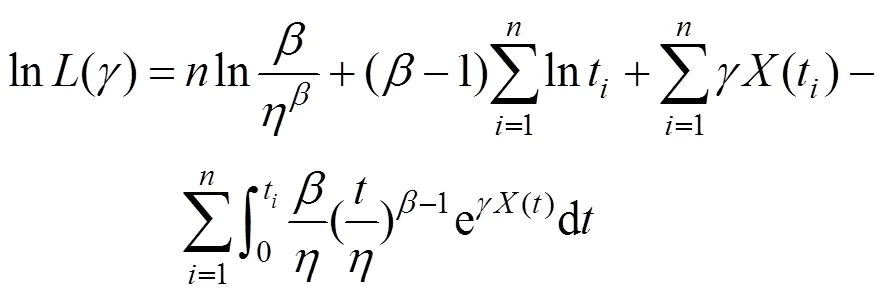
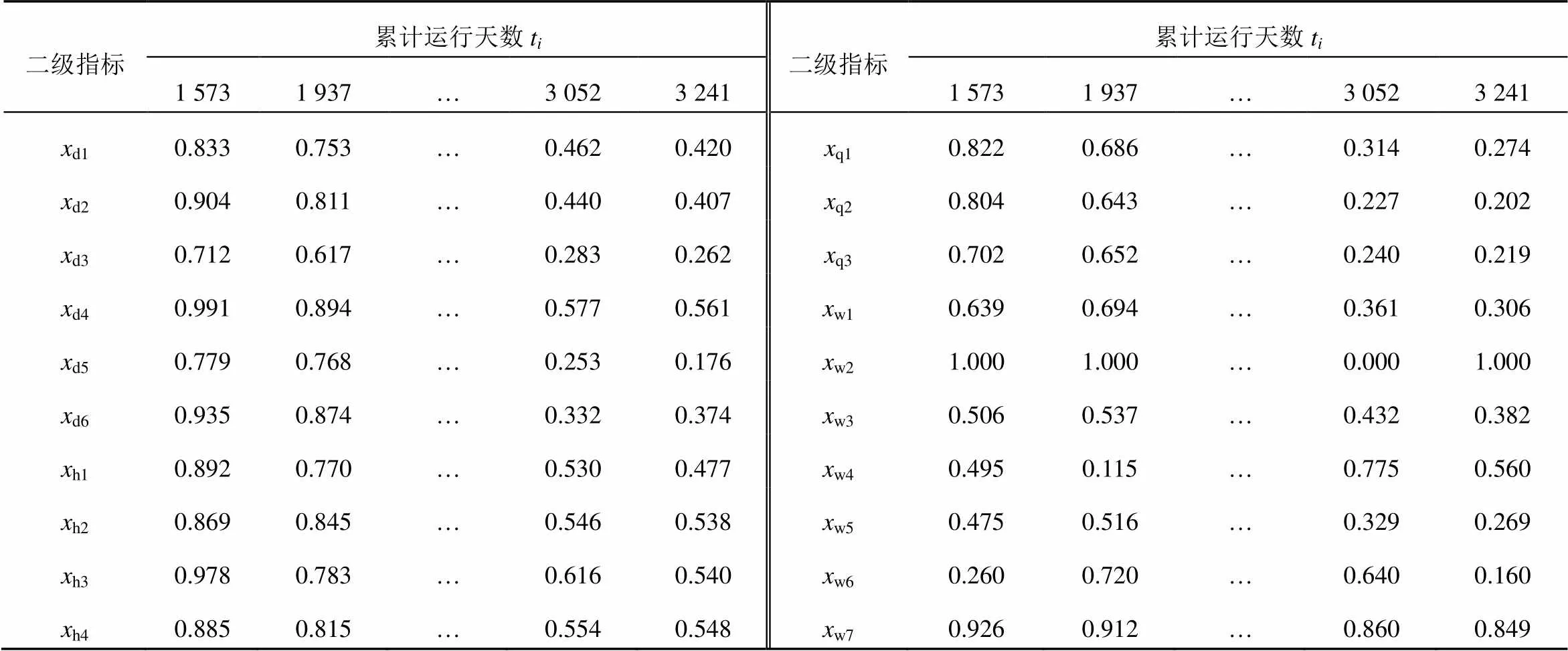
表3 二级指标状态量的标准化值（部分）

为便于计算，设在t–t+1间隔较小的时间段内，各二级指标的监测值不发生突变，结合微元法的思想将式（8）中的积分项表示为式（9）。将式（9）代入式（8）后对(=1,2,3,···,)求偏导得到式（10），令该式为0后采用牛顿–拉夫逊迭代法求解式（10）中个回归系数。

运用MATLAB软件进行计算，得到参数，和回归系数分别如表4和表5所示。经过计算表明在估计相同数量参数的前提下，该方法比极大似然估计的分步计算方法[18]快了0.3~0.5 s，比传统的极大似然估计整体计算方法快了10~21.5 s，且误差保持在0.01以内，在一定程度上提高了运算速度。

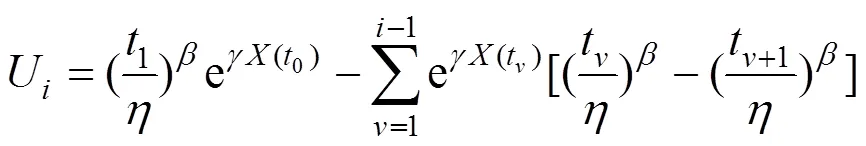
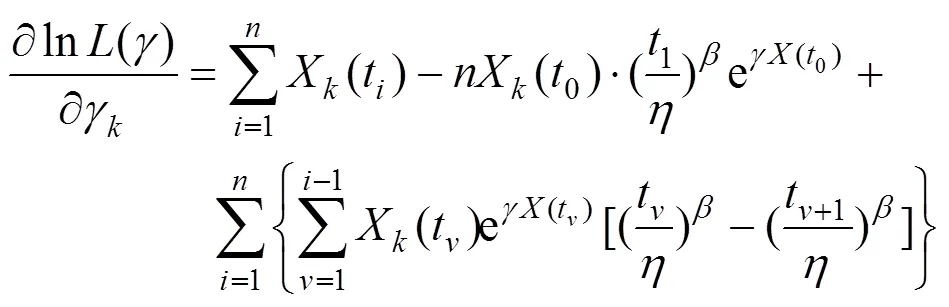
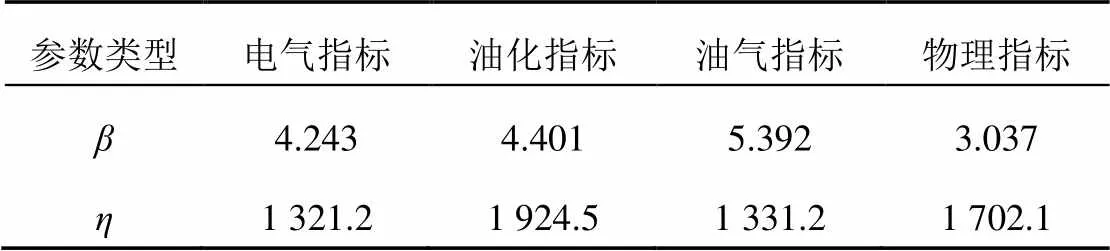
表4 各一级指标形状参数和尺度参数

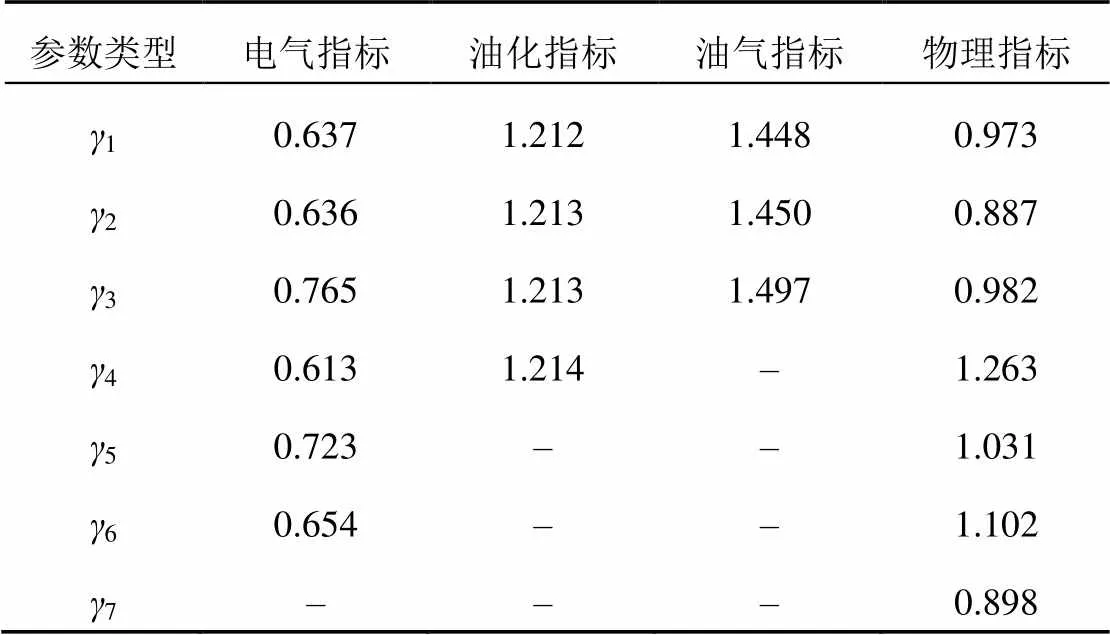
表5 各一级指标对应二级指标的回归系数

2.2 模糊综合评估模型

模糊综合评估是指利用模糊数学中的隶属度理论对不同事物所表现出的不同特性进行归一性评估的方法。结合各一级指标的风险度值，利用模糊综合评估就可以得到变压器当前所属的风险水平，进而可预测维修周期，制定相应的检修策略。

将变压器4个一级指标的风险度值作为模糊综合评价模型的指标集=(1,2,3,4)。为了更好地描述变压器的运行风险，本文采用良好、正常、警戒、危险4种状态来进行状态评价。变压器模糊综合评估的计算模型如式（11）所示。其中为权重向量，为模糊关系矩阵。

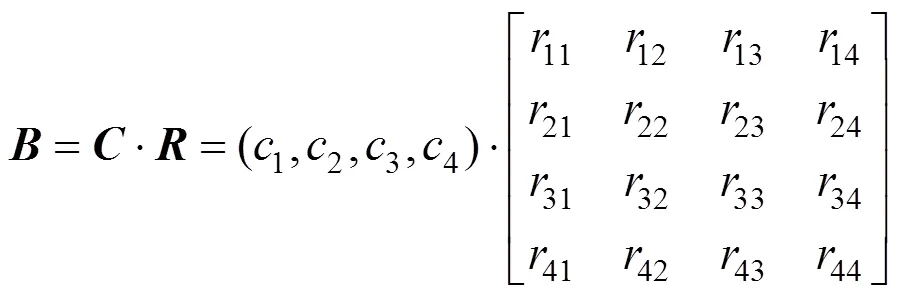
2.2.1 权重的确定

为更好地凸显异常指标对评价结果的影响，提高评估的准确性，本文采用基于变权理论的层次分析法确定变压器各指标的权重。该方法可让权重与指标实时监测值相关联，使权重随着指标监测值的变化进行动态调整。

根据各一级指标的重要程度构建如式（12）所示的判断矩阵。求得判断矩阵的最大特征根max=4，将max对应的特征向量归一化后得到各指标的初始权重向量0=[0.162, 0.243, 0.487, 0.108]。

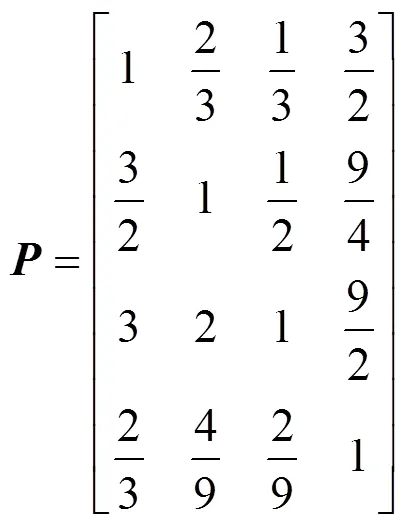
将初始权重和标准化后的一级指标按照式（13）计算，可得到实时状态下各指标的变权重。其中c为指标u的变权重，0i为指标u的初始权重，x为指标u的标准化值。

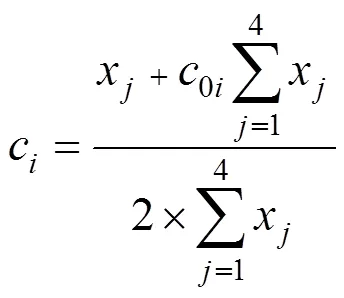
2.2.2 基于改进隶属函数法的模糊关系矩阵

为保证变压器各一级指标在评价时的模糊隶属性，本文采用如图2所示的改进岭形分布作为隶属函数构建模糊关系矩阵。其中1、2、3、4为隶属函数的边界参数，变压器健康状态()随风险值的增加而恶化。

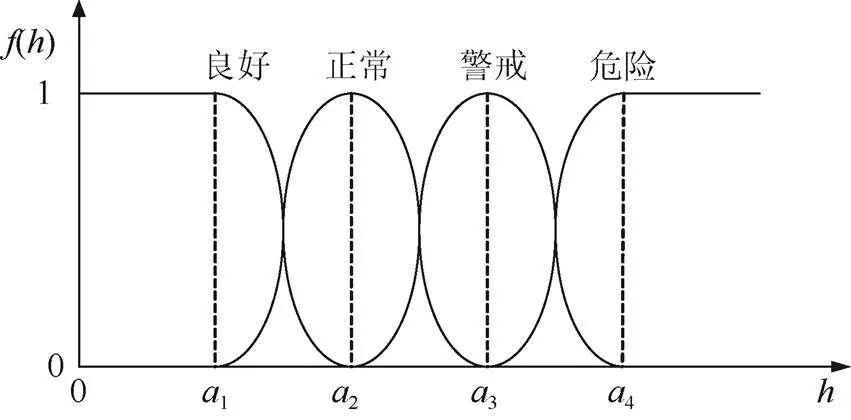
图2 改进的岭形隶属函数分布

结合图2所示的分布曲线，变压器各一级指标风险值对应良好、正常、警戒、危险4种状态的隶属函数分别如式（14）~（17）所示，将状态指标数值代入式中，即可得到变压器各一级指标风险度与健康状态的模糊关系。

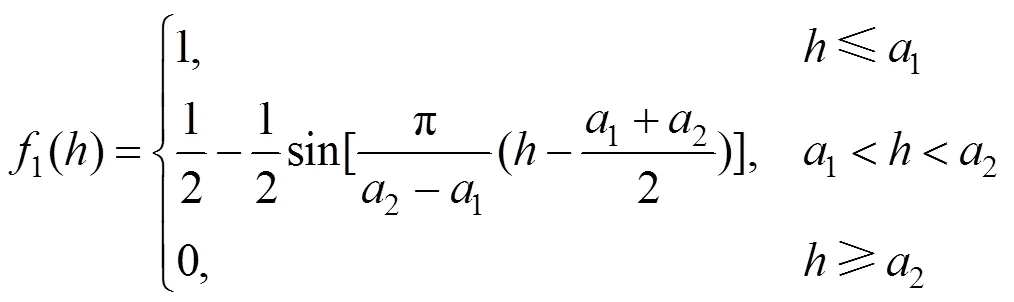
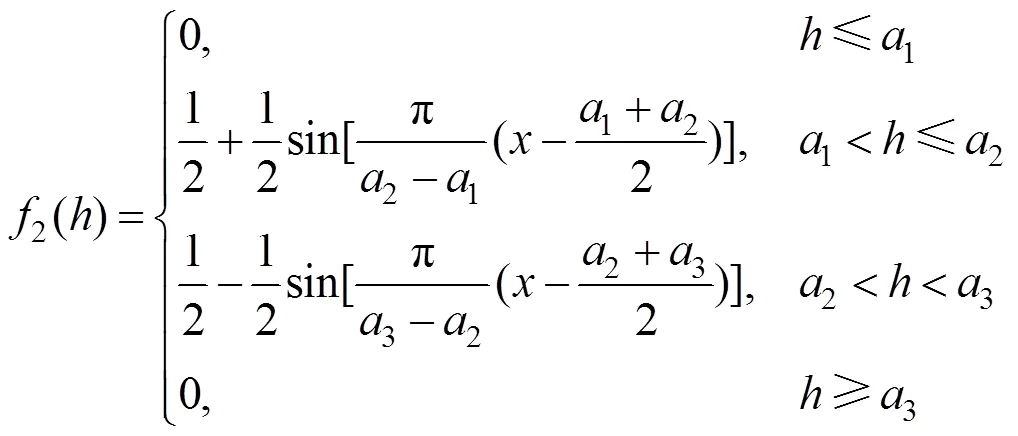
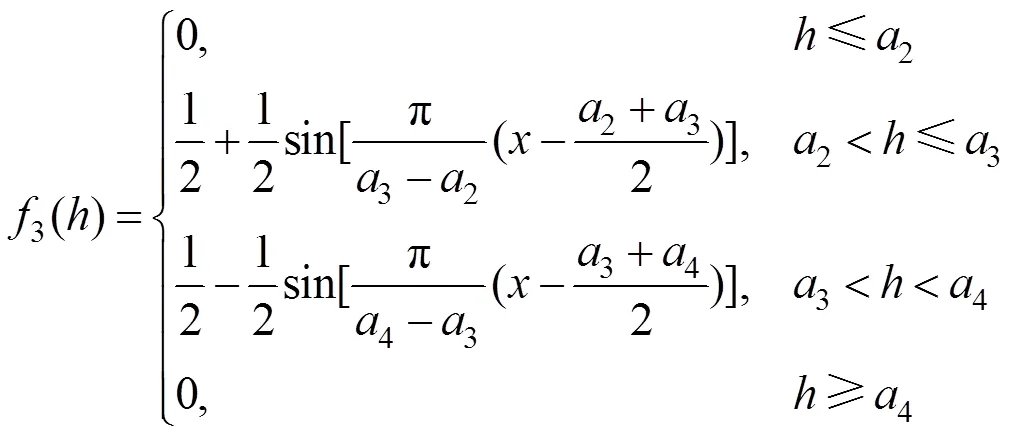
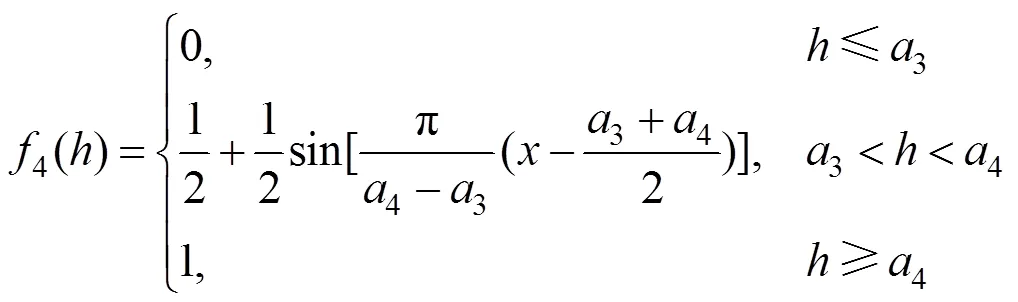
由于边界参数1、2、3、4反应各指标风险值的大小，而风险值又是可用度（可靠度）的直接体现，因此本文提出采用基于可用度最优的方法确定4个边界参数。

设备可用度指设备指定时间段内能够保持正常工作的能力，可用该时间段内保持指定能力的时间与总时间的比值来表示：

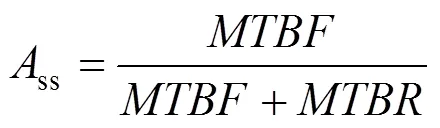
式中：ss为稳态可用度；为平均保持指定能力时间；为平均失去指定能力时间。

变压器维修有两种条件：一种是变压器运行到给定役龄，另一种是变压器未达到给定役龄的情况下发生失效。从以上两种情况可知，变压器的维修时间是一个随机变量，变压器的工作时间符合如下分布函数：

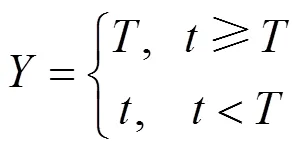
式中：为变压器运行时间；为变压器给定役龄。

变压器未维修前的时间为保持指定能力时间，其表达式如式（20）所示。

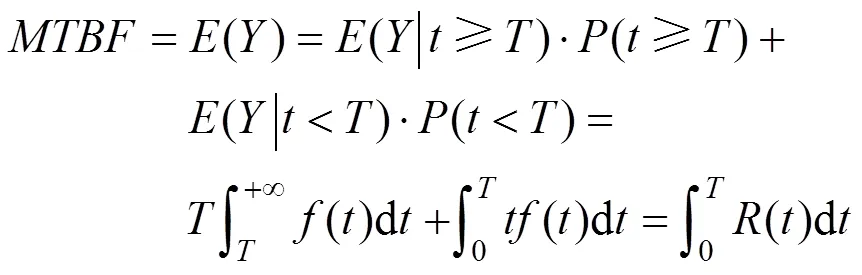
设变压器在达到指定情况进行维修需要花费的时间p为20天。变压器在良好、正常、警戒、危险4种状态下进行维修需要花费的时间f分别为2天、4天、6天、8天，将p、f代入式（21）得到平均失去指定能力时间。

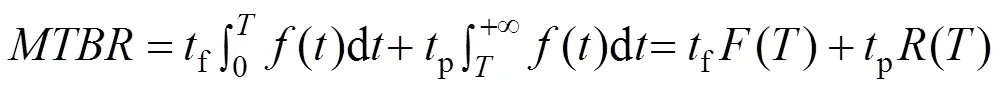
将式（20）和式（21）代入式（18）对役龄时间求偏导，令偏导数为0得到式（22），参照状态指标函数()中回归系数的估算方法，得到在给定维修方式下，保持可用度为最大值时对应的最优维修时间best，再将best及其对应的状态指标监测值代入式（5）得到该维修方式下对应的风险值。按式（18）~（22）计算可得到如表6所示的变压器在良好、正常、警戒、危险4种状态下的最优可用度ss及其对应的最优维修时间。

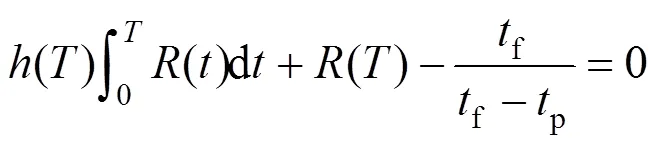
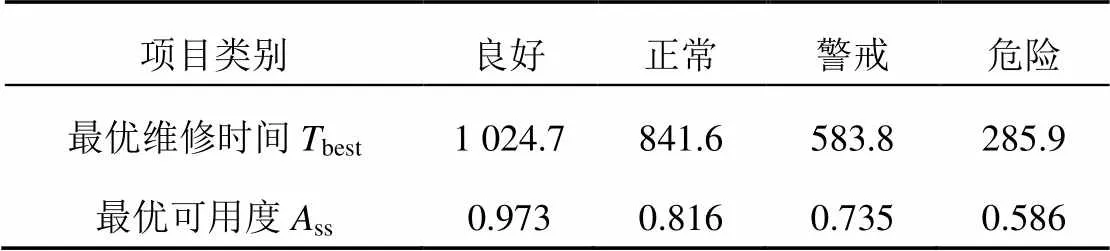
表6 良好、正常、警戒、危险4种状态下对应最优维修时间及最优可用度

将最优维修时间分别代入4个一级指标的风险函数中，可以得到如表7所示的各一级指标边界参数1、2、3、4，将各边界参数代入对应的隶属度函数，可得到如图3所示的各一级指标的隶属度函数图像。

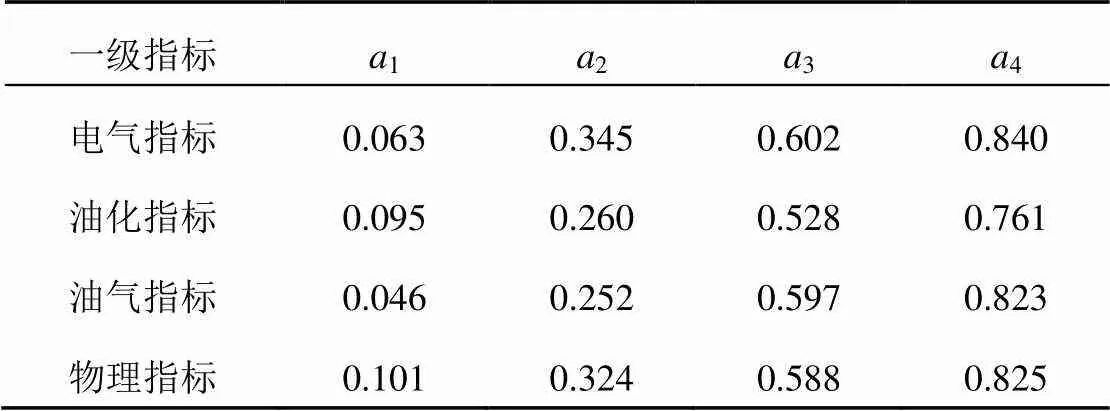
表7 一级指标边界参数

图3 各一级指标的隶属度函数图像

Fig. 3 Image of each primary index’s membership function

3 实例分析

为验证所提出状态评估方法的有效性和实用性，本文从福建、河北等地电厂中选取了5台SFSZ-34000/220型油浸式变压器进行实例分析，其中，G1为正常运行的变压器，G2~G5为4台故障变压器。对上述变压器建立状态指标体系，得到各变压器二级指标的标准化值如表8所示。

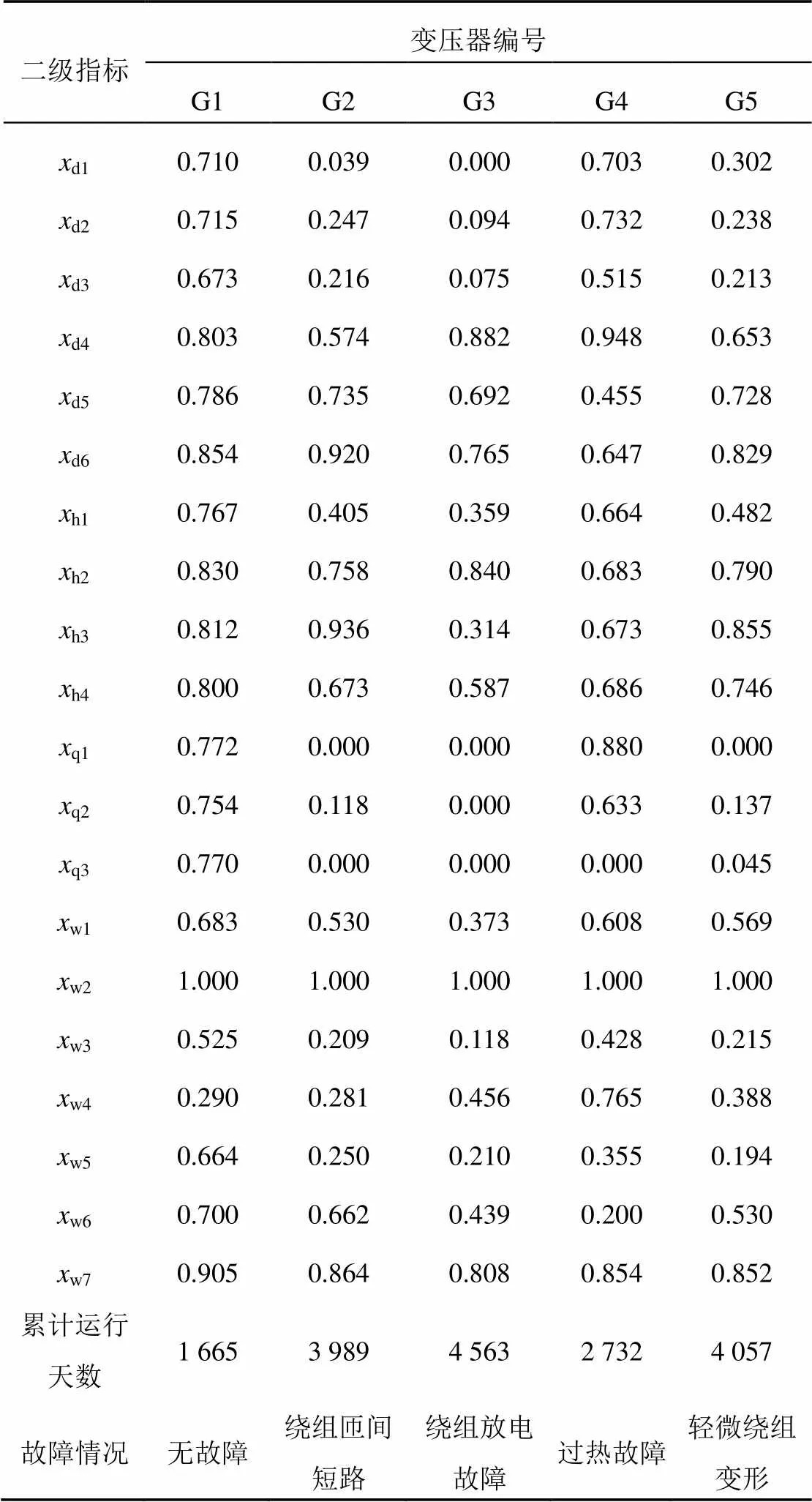
表8 实例变压器二级指标状态量的标准化值

将表8中的二级指标标准化值代入上文构建的WPHM风险度模型中，得到5台变压器各一级指标的风险度计算值如表9所示。由表中可以看出无故障运行的G1变压器4个一级指标的风险值都很低，均远小于0.5；另外4台发生故障的变压器按故障类型和故障程度的不同均含有风险值远大于0.5的一级指标，进而证明了建立的WPHM风险度模型与变压器的实际状况相符合。

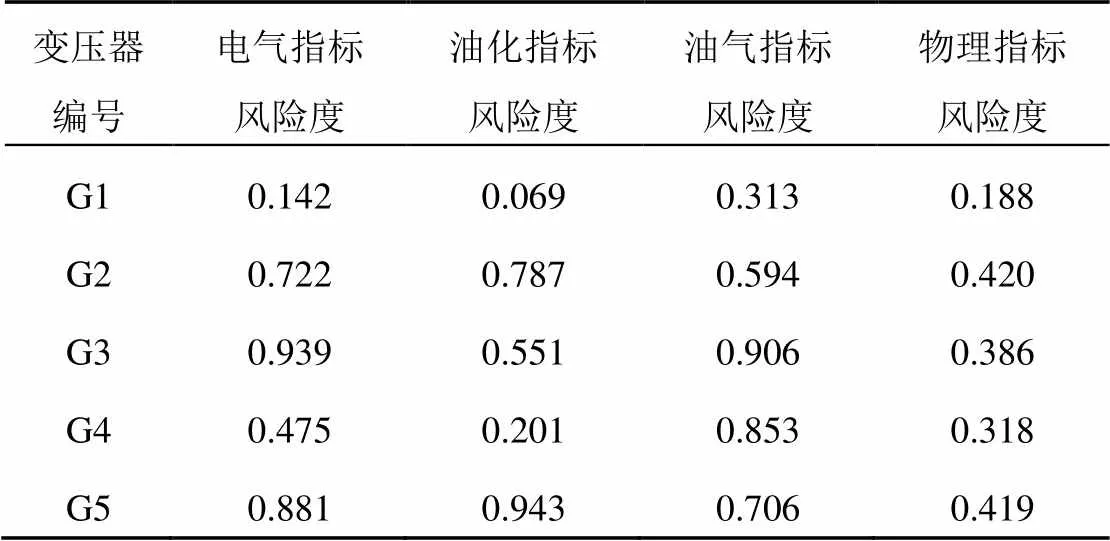
表9 各一级指标风险度计算值

由上文中提出的权重计算方法可以得到进行实例分析的5台变压器的权重向量分别为：

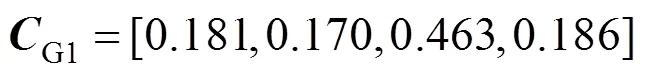
由式（14）~（17）中的隶属函数得到的5台变压器的模糊关系矩阵为：

根据式（11）中的模糊综合评估模型可以得到5台变压器整体上隶属于良好、正常、警戒、危险4种状态的比例分别为：

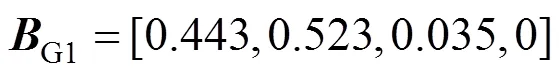
图4展现了5台实例变压器整体的状态评估情况：G1变压器处于正常状态，G2变压器处于警戒状态，G3、G4和G5变压器均处于危险状态，5台变压器的整体状态评估结果与实际状况相符，进一步验证了本文评估方法的正确性。

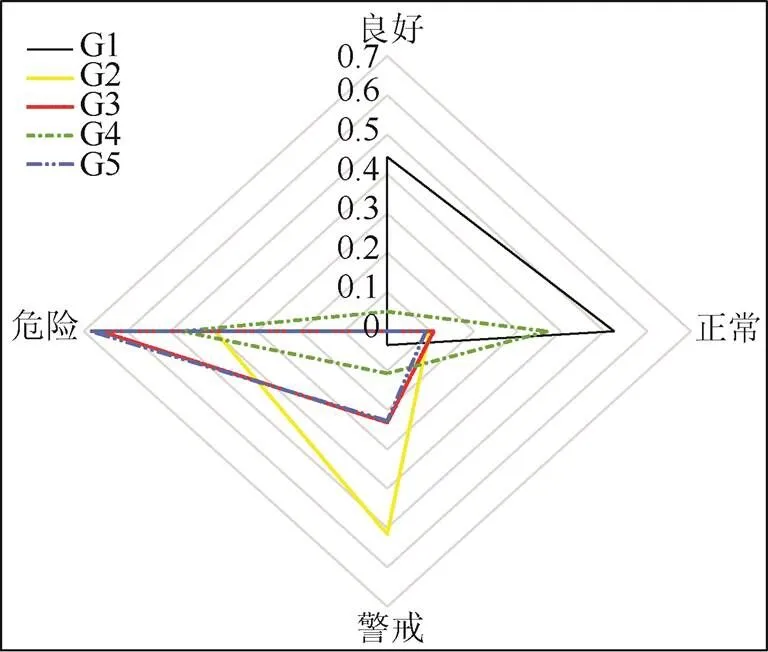
图4 5台变压器整体的状态评估分布

4 结论

本文提出了一种将WPHM模型和模糊综合评估相结合的变压器健康状况评价方法，与传统的变压器状态评估方法相比，该方法具有如下特点：

（1）从电气、油化、油气和物理4种性质上构建了两级状态指标体系，提高了信息的采集和监测效率，全面分析了变压器各种性质的风险度，在一定程度上为检修策略的的制定指明了方向。

（2）对各种性质的一级指标建立WPHM模型，提出了采用威布尔概率图法和极大似然估计法相结合的参数估算方法，在保证准确性的前提下缩短了参数计算时间，更适合工程上的实际应用。

（3）以一级指标风险度为基础，引入变权理论和最优可用度法，采用改进隶属函数法对变压器整体健康状态进行模糊综合评估。通过对5台变压器进行实例分析，评估结果与实际的工况相吻合，验证了该方法在变压器状态评价上的准确性、合理性和有效性，为发电厂变压器状态检修提供指导和支撑。

[1] 章亮, 杨俊杰. 基于多维正态云模型的电力变压器状态评估[J]. 电测与仪表, 2020, 57(4): 129-135. ZHANG LIANG, YANG JUNJIE. State assessment of power transformers based on multi-dimensional normal cloud model[J]. Electrical Measurement & Instrumentation, 2020, 57(4): 129-135(in Chinese).

[2] 朱江行, 邹晓松, 赵真, 等. 基于改进TOPSIS灰色关联分析的变压器状态评估方法[J]. 电力科学与工程, 2020, 36(8): 30-36. ZHU JIANGHANG, ZOU XIAOSONG, ZHAO ZHEN, et al. Transformer condition assessment method based on improved TOPSIS and grey correlation analysis[J]. Electric Power Science and Engineering, 2020, 36(8): 30-36(in Chinese).

[3] 郭世波. 内蒙古包头东河110 kV变电站状态检修改造方案[D]. 天津: 天津大学, 2016. GUO SHIBO. The renovation plan of condition-based maintenance for 110 kV Donghe substation in Baotou Inner Mongolia region[D]. Tianjin: Tianjin University, 2016(in Chinese).

[4] 肖艳炜, 楼平, 蒋水中, 等. 电力网络环境下的变压器故障诊断技术研究[J]. 变压器, 2019, 56(4): 46-50. XIAO YANWEI, LOU PING, JIANG SHUIZHONG, et al. Research on transformer fault diagnosis technology in power network environment[J]. Transformer, 2019, 56(4): 46-50(in Chinese).

[5] 何文林. TOPSIS法在变压器绝缘状态评估中的应用[J].浙江电力, 2019, 38(9): 69-73. HE WENLIN. Application of TOPSIS in transformer insulation state evaluation[J]. Zhejiang Electric Power, 2019, 38(9): 69-73(in Chinese).

[6] 袁志坚, 孙才新, 袁张渝, 等. 变压器健康状态评估的灰色聚类决策方法[J]. 重庆大学学报(自然科学版), 2005, 28(3): 22-25. YUAN ZHIJIAN, SUN CAIXIN, YUAN ZHANGYU, et al. Method of grey clustering decision-making to state assessment of power transformer[J]. Journal of Chongqing University(Natual Science Edition), 2005, 28(3): 22-25(in Chinese).

[7] 王文宾, 白文广, 石磊磊, 等. 电力变压器全寿命周期经济–物理综合寿命评估方法[J]. 电力系统保护与控制, 2019, 47(4): 91-98. WANG WENBIN, BAI WENGUANG, SHI LEILEI, et al. Evaluation method of power transformers full life cycle economic-physical comprehensive life[J]. Power System Protection and Control, 2019, 47(4): 91-98(in Chinese).

[8] 张博, 吴杰康, 罗伟明. 基于模糊理论和证据理论的变压器绝缘老化状态评估[J]. 广东电力, 2019, 32(8): 109-118. ZHANG BO, WU JIEKANG, LUO WEIMING. Transformer insulation aging state assessment based on fuzzy theory and evidence theory[J]. Guangdong Electric Power, 2019, 32(8): 109-118(in Chinese).

[9] 郭创新, 高振兴, 张健, 等. 油浸式电力变压器状态评估模型及方法[J]. 控制工程, 2011, 18(6): 881-885. GUO CHUANGXIN, GAO ZHENXING, ZHANG JIAN, et al. On model and approach of condition assessment of oil-immersed transformer[J]. Control Engineering of China, 2011, 18(6): 881-885(in Chinese).

[10] 王楠, 王伟, 张鑫, 等. 改进的层次分析法在变压器油纸绝缘状态评估中的应用[J]. 高压电器, 2019, 55(12): 187-192. WANG NAN, WANG WEI, ZHANG XIN, et al. Application of improved analytic hierarchy process in transformer oil-paper insulation state evaluation[J]. High Voltage Apparatus, 2019, 55(12): 187-192(in Chinese).

[11] 刘瑞英. 电力变压器状态评估方法的研究[D]. 吉林: 东北电力大学, 2017. LIU RUIYING. Research on the method of power transformer condition evaluation[D]. Jilin: Northeast Electric Power University, 2017(in Chinese).

[12] 中华人民共和国电力工业部. 电力设备预防性试验规程: DL/T596-1996[S]. 北京: 中国电力出版社, 2019. Ministry of Power Industry of the PRC. Preventive test procedure for power equipment: DL/T596-1996[S]. Beijing: China Electric Power Press, 2019 (in Chinese).

[13] 中华人民共和国国家质量监督检验检疫总局. 变压器油中溶解气体分析和判断导则GB/T 7252-2001[S]. 北京: 中国电力出版社, 2015. AQSIQ. Guide for analysis and judgment of dissolved gases in transformer oil GB/T 7252-2001[S]. Beijing: China Electric Power Press, 2015 (in Chinese).

[14] 叶清, 吴晓平, 白春杰. 一种系统状态评估方法及其应用[J]. 武汉理工大学学报, 2006, 28(5): 108-112. YE QING, WU XIAOPING, BAI CHUNJIE. An assessment method for systems’ state and its application[J]. Journal of Wuhan University of Technology, 2006, 28(5): 108-112(in Chinese).

[15] 高曦莹, 潘明明, 王志斌, 等 . 基于技术经济比较的低压用户业扩报装供电方案综合评价[J]. 供用电, 2019, 36(10): 61-66. GAO XIYING, PAN MINGMING, WANG ZHIBIN, et al. Comprehensive evaluation of power supply scheme for business expansion of low voltage users considering technical and economic comparison[J]. Distribution & Utilization, 2019, 36(10): 61-66(in Chinese).

[16] 葛晶晶. 基于Markov过程的网络控制系统冗余技术研究[D]. 大连: 大连理工大学, 2014. GE JINGJING. Research on redundancy technology in network control system based on Markov process[D]. Dalian: Dalian University of Technology, 2014(in Chinese).

[17] 喻勇, 司小胜, 胡昌华, 等. 数据驱动的可靠性评估与寿命预测研究进展: 基于协变量的方法[J]. 自动化学报, 2018, 44(2): 216-227(in Chinese). YU YONG, SI XIAOSHENG, HU CHANGHUA, et al. Data driven reliability assessment and life-time prognostics: A review on covariate models[J]. Acta Automatica Sinica, 2018, 44(2): 216-227(in Chinese).

[18] 张路朋, 王娟, 王攀, 等. 一种新的威布尔比例失效模型参数估计方法[J]. 河北电力技术, 2017, 36(5): 18-20. ZHANG LUPENG, WANG JUAN, WANG PAN, et al. A new method of parameter estimation for Weibull proportional failure model[J]. Hebei Electric Power, 2017, 36(5): 18-20(in Chinese).

Health Condition Evaluation of Transformer Based on WPHM Model and Fuzzy Comprehensive Evaluation

ZHENG Wenguang1, XIE Hongling2, LI Yanqing2, WANG Aijun3, WANG Guan3, ZHANG Xiaowen4

(1. Douhe Power Plant, Datang International Power Generation Co., Ltd., Tangshan 063000, China; 2. School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China; 3. Tangshan Meteorological Bureau, Tangshan 063000, China; 4. Department of Resources Management, Tangshan Normal University, Tangshan 063000, China)

Aiming at solving condition evaluation problems such as large fuzziness, one-sided evaluation index and weak guidance, this paper puts forward a transformer condition evaluation method based on WPHM model and fuzzy comprehensive evaluation. This method firstly establishes a two-stage condition index system from four properties of electricity, oilization, gas and physics, which improves the evaluation comprehensiveness and information acquisition efficiency. Then, WPHM model is built to comprehensively analyze the risk of primary index based on the secondary index, and the parameters are estimated by Weibull probability graph method and maximum likelihood estimation method, which improves the computational speed of the parameters. Finally, combined with the theory of optimal availability, the membership function is constructed and used to obtain the fuzzy relation between transformer risk degree and condition, and then the overall risk level of transformer is obtained under the action of variable weight. After a case study, the evaluation method is proved to be objective, accurate, convenient and effective, which has good practicability in engineering and can provide guidance and help for transformer maintenance.

transformer; WPHM model; fuzzy comprehensive evaluation; health condition evaluation

10.3969/j.ISSN.1672-0792.2021.02.005

TM41

A

1672-0792(2021)02-0032-10

2020-11-02

唐山市气象局科研开发项目（18ky02ts）；唐山师范学院博士基金（2019A10）

郑文光（1994—），男，硕士研究生，研究方向为电气设备状态检测与故障诊断、模式识别与智能系统等；

谢红玲（1973—），女，讲师，研究方向为电气设备故障诊断、高电压与绝缘技术等；

李燕青（1974—），男，教授，研究方向为电网规划、新能源发电与微电网控制等。

郑文光