水下声学超材料研究
2021-03-17曹培政
曹培政,张 宇,2,3,刁 顺,张 赛
(1.厦门大学海洋与地球学院 水声通信与海洋信息技术教育部重点实验室,福建 厦门 361005)(2.麻省理工学院机械工程系,美国麻萨诸塞州 剑桥 02139)(3.厦门大学海洋与地球学院 近海海洋环境科学国家重点实验室,福建 厦门 361005)(4.江苏大学物理系,江苏 镇江212013)
1 前 言
超材料是一种具有超常物理性质的人工复合材料,通过对其微结构的有序设计,可突破某些自然规律的限制,产生天然材料所不具备的物理性质,在某种程度上实现对光波、电磁波和声波的超常规传输。
声学超材料是人为设计的由两种或两种以上材料构成的周期性或非周期性几何结构,结构尺寸远远小于声波波长,展现出许多奇异的物理现象和超常规声学效应。近年来,声学超材料在空气中的研究十分丰富,在实现负折射、波束控制以及声定向传输等方面起到了重要的作用。
声学超材料在空气中的良好应用也让更多的研究者们聚焦到了水下声学超材料(简称水声超材料)的研究。但是,由于声波在水下的传播比较复杂,并且水下的研究涉及到流体和固体两相介质之间相互作用的影响,加大了研究的难度。水下研究的主要难题在于水下尺度大、低频性能差、不耐静水压力等,这也是目前研究者们努力突破的方向。例如,水下吸隔声是水下声学研究的重点,但要找到一种小尺寸、宽频带的设计一直是难点。经典的局域共振型超材料通过对参数进行设计,拓展了低频吸声带宽,产生了如基于多层局域共振声学超材料(LRAM)的宽带吸声板结构,在相应的共振频率下,板的每一层都可以作为一个近似独立的单元振荡,宽带吸声器的吸声性能明显优于只含一种局部共振散射体的吸声器。
水声超材料从经典的局域共振型不断延伸:超晶格超表面复合结构,实现了另一类具有广泛水下应用的超材料结构,应用领域包括噪声控制、声学通讯、目标探测等;结合仿生应用,进行了基于声速梯度的水下仿生波束控制研究,为水下亚波长声纳、医学超声等声学应用提供了参考。通过这些研究可以看出,声学超材料在水下的应用广泛,具有十分广阔的前景。
2 水下局域共振型声学超材料
传统的局域共振型超材料突破了质量-密度定律,几种理论和数值方法可以分析传统局域共振型超材料,如平面波展开法[1-3]、多重散射理论(MST)[4]、时域有限差分法(FTDT)[5]等。
水下吸隔声一直是近年来的研究重点,但要找到一种小尺寸、宽频带的设计一直是难点。而声学超材料技术可以通过亚波长人工结构设计突破普通材料的限制,其特殊的物理效应在声学领域,尤其是在水下这种要求苛刻的环境下,有着巨大的应用潜力。
初期吸声研究的是具有空气腔的水下消声涂料的优化设计[6, 7]。然而,由于共振频率依赖于腔体的体积,在无回声层厚度有限的情况下,如何提高低频吸收是一个难题。为了改善粘弹性材料的低频水声吸收性能,引入了局部共振单元[8, 9],嵌入相同单元的均匀层表明高吸收只发生在较窄的频率范围内。将不同共振频率的局部共振层结合起来,可以实现水声在低频范围内的宽带吸收,有利于消声涂料的设计。
传统的声学超材料是一种人工合成材料,其部分内含物/散射体在空间上周期性分布,嵌入基体/基体材料中,机理分析是布拉格散射和局域共振形成的能量带隙来控制声波的传输。其中局域共振型超材料比相同晶格常数的布拉格超材料带隙小近两个数量级,所以其可以在低频情况下研究声衰减等问题。
Hladky-Hennion等[10]用有限元法分析了平面声波在双层周期结构中的散射特性,结果表明,有限元法用于研究这些光栅的行为是准确可行的。
有研究表明,嵌有共振声波材料的粘弹性板的局域共振模式对该材料的吸声性能有重大影响[11]。Leroy等提出了基于等效介质理论的半解析模型,用于研究周期性空化的软弹性介质在水下的声学特性[11],Zhao等通过实验验证了局域共振在水声吸声方面的可行性[12]。进一步地,通过改变背衬材料、优化复合局域共振的驻波共振吸收[13],分析局域共振影响下的结构参数对吸声性能的影响[14]。Meng等[15]将不同的局域共振体嵌入到声学超材料中,并对局域共振型超材料结构参数进行优化,这些都可以拓展低频吸声带宽。考虑到静水压力对结构吸声性能的影响,Jiang等[16, 17]将互穿网络嵌入到传统的局域共振材料中,实现了高静水压力条件下的强宽带吸声。
综上,局域共振型超材料在水下应用有一定的限制性,为了改进局域共振型超材料在水声中的带宽局限以及受尺寸影响等问题,进行了如下探究。
2.1 局域共振二维水声超材料
局域共振型超材料在空气中的研究较多,近年来其在水下的研究也逐渐增多,但由于水中静压力、流体耦合等因素的影响,单个散射体的共振特性与基体中长波的相互作用会受影响,如何设计单个散射体共振特性以及基体长波行波特性是关键。
集合以上探索,2019年,Zhong等[18]提出了一种具有螺旋谐振腔的水下低频吸声超材料,其由粒子填充聚氨酯(PU)阻尼复合材料和方形螺旋腔构成。如图1所示,该水声超材料结构是由二维形式的三明治圆柱形板构成,包括一个薄的弹性核心层和两个相同的薄的弹性面层,且在面内周期性分布。层间为多孔软弹性颗粒填充聚氨酯阻尼复合材料,核心层材料为周期性螺旋薄弹性板。所述谐振腔具有两个面孔和一个中心构件的螺旋结构,从而形成螺旋谐振腔。
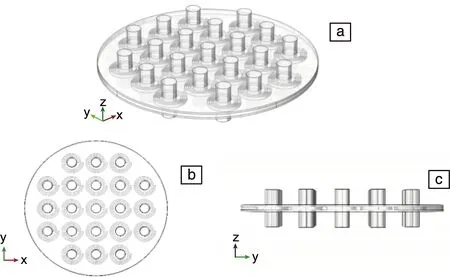
图1 包含21个周期单元的水声超材料结构示意图(a),该结构的俯视图(b)和侧视图(c)[18]Fig.1 Schematic illustration of the underwater acoustic metamaterial structure with 21 periodic cells (a), top view (b) and side view (c) of the metamaterial structure[18]
图2a为一个周期细胞在水中平面波垂直入射下的模型图。其结构复杂,吸声系数是几何参数和材料参数的非线性函数,通过参数分析很难得到理想的吸声系数。为了进一步研究周期单元的共振特性,可以将单元简化为一个弹簧-质量系统。在入射弹性波的作用下,振动在超材料结构中产生,通过一个核心层和两个面层到达圆柱体。3种振动的等效质量和刚度元素(即圆柱体、芯层和面层)分别表达为(m,Mc,Mf),(k,Kc,Kf)。然后由简谐力p0sin(ωt)激发的无阻尼系统方程可以由矩阵运算等式表示:
(1)
式中,p0为入射波的振幅,ω为声波频率,代入通解x=x0sin(ωt)和X=X0sin(ωt),可以得到振动系统的谐波响应幅值为:
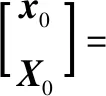
(2)
式中,ω1和ω2为固有模态频率。当圆柱体与核心层螺旋梁发生共振时,由于施加在结构上的激励受到(M-k)系统力的抵消,3层(Mc+2Mf)的位移降为零。当使用螺旋谐振器作为超材料的结构单元时,弹性波在某些频域内可能不会在所提出的超材料结构中传播,这意味着会形成带隙,带隙特性有利于提高该结构的水下吸声性能。
基于布洛赫-弗洛凯定理,将周期边界条件应用于所提出的超材料平板的周期单元之间的界面。由于超材料板在x、y方向具有周期性且周期单元具有对称性,特此引入了布洛赫(Bloch)波矢量k,并在不可约布里渊区的边界上有一个值。通过改变布里渊区的布洛赫波矢量,求解本征值问题,可以得到能带结构。如图2b所示,通过沿色散图右侧所示的布里渊区的边界线扫描约简布洛赫波矢量,计算出了所提出的超材料结构的色散图。可以看出,超材料结构在主频[2.2 kHz, 3.3 kHz]中具有完整的带隙。在谐振频率沿任意方向保持不变的全带隙中,水下声波能量不能在原材料板中传播,而是局限在单位周期单元的每个螺旋谐振腔中,然后由于机械阻尼的阻尼振荡而大大衰减。此外,从声波衰减的角度看,可以通过周期性单元的局部共振散射来提高多孔软弹性颗粒填充聚氨酯阻尼材料中入射声波纵波转化为横波的效率。由于横波在多孔软弹性颗粒填充聚氨酯阻尼材料中具有很高的耗散效率,只有少量的横波能再次转化为声波纵波,从而降低了材料的耗散效率。此外,还进行了模态分析,得到了能带结构中各支路的特征振型。
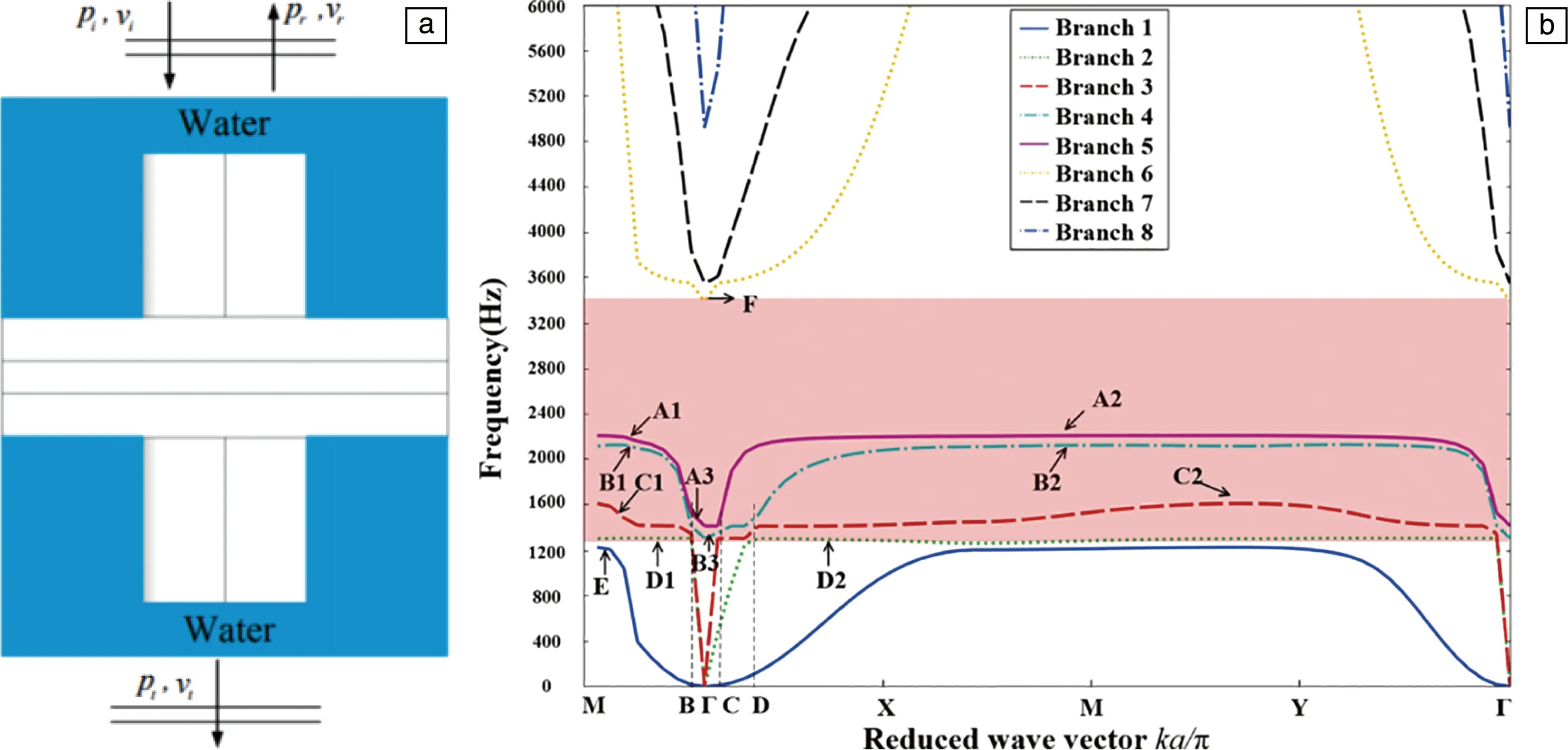
图2 在平面波垂直入射的情况下的超物质结构周期单元的理论模型(a),所提出的超材料结构的色散图(b)[18]Fig.2 The theoretical model of periodic cell of metamaterial structure under normal incidence of plane wave in the water(a), dispersion diagram of metamaterial structure(b)[18]
研究发现,该结构的局部共振带隙削弱了高静水压力对材料吸声性能的影响。所提出的超材料板为今后水下超薄声学超材料的结构设计和应用提供了指导。
螺旋谐振腔超材料提供了一种超材料在水下环境研究中的解决方式,降低了静水压力影响。但其也有有效带宽太窄、结构较复杂等缺点,如何解决此类问题,需要在结构形式等方面继续研究。
2.2 多层局部共振散射体的水声超材料的吸声性能
为了拓展水声超材料有效吸声的频率范围。Shi等[19]提出了一种具有多层圆柱散射体的新型局域共振型超材料(M-LRAMs)(图3),分析带隙特性和吸声性能,采用有限元法计算本征模型的位移场和吸声系数。此外,还研究了各种结构参数和材料参数对吸声性能的影响。
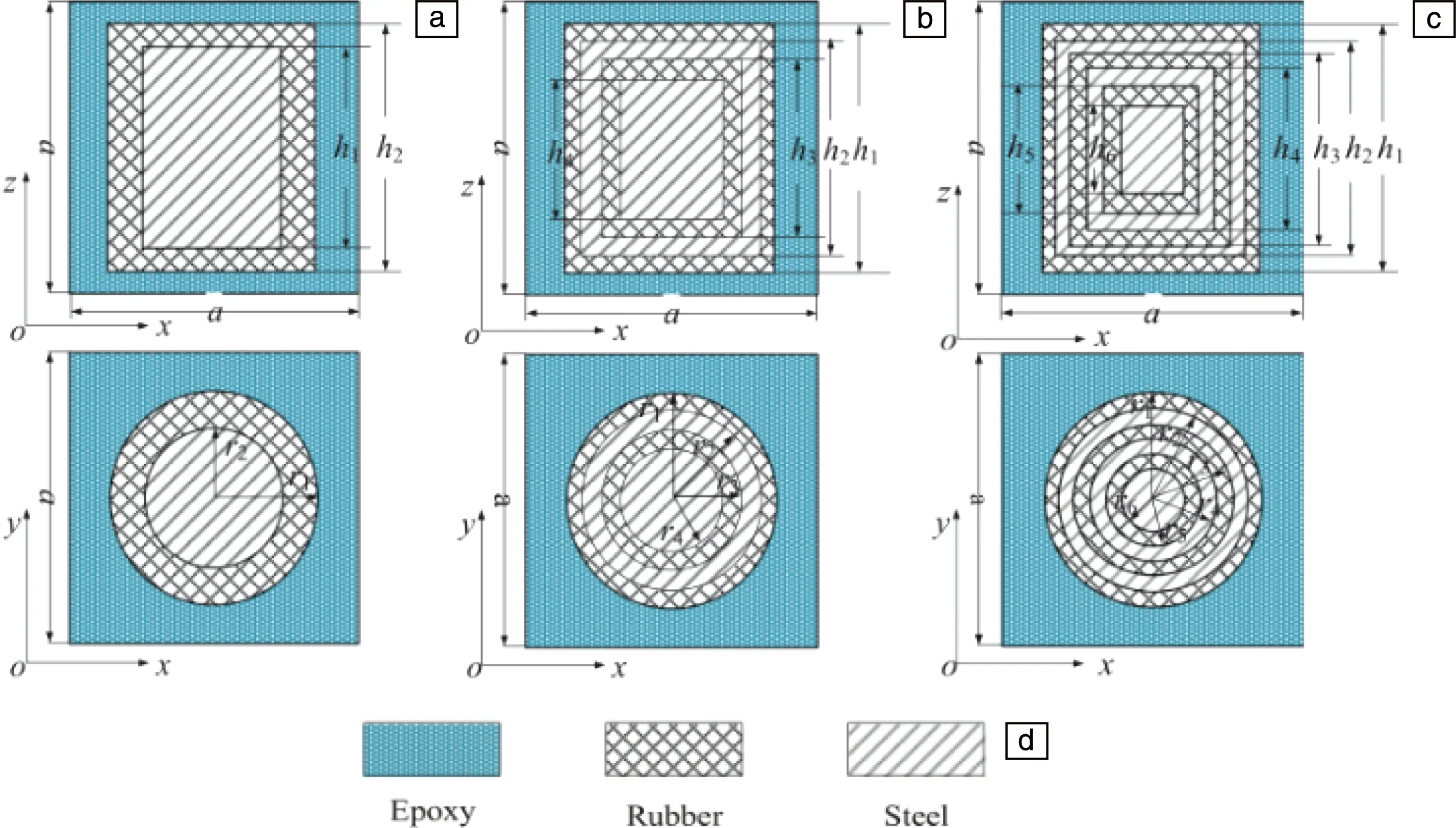
图3 3种模型单元的横截面[19]:常规LRAMs(a),具有双层(b)和3层(c)柱状散射体的LRAMs,元器件的材料示意图(d)Fig.3 The cross-section for a unit cell of the three model[19]: the conventional LRAMs (a), the LRAMs with double-layered (b) and three-layered (c) cylindrical scatterers, the schematic diagram of materials for components (d)
弹性结构控制方程见式(3)[20]:
(3)
式中,t为时间,cijkl为弹性常数,ρ表示质量密度,ui表示位移,xj代表坐标变量。
根据有限元理论,单元的特征值方程可以表示为式(4):
(K-ω2M)U=0
(4)
式中,K和M分别表示单元格的刚度矩阵和质量矩阵。U为节点的位移矢量。采用有限元法对模型的固有频率和频散关系进行分析,传输函数TF定义为式(5):
(5)
式中,ui和ut分别为流体域中的入射和透射位移,声波传输方程可以表示为式(6):
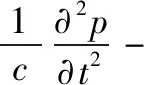
(6)
正反射系数R和透射系数T可以定义为式(7)[15]:
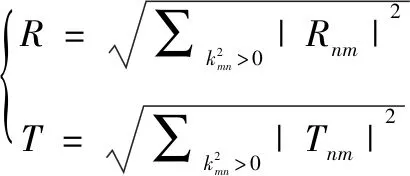
(7)
(8)
m和n分别表示平面波展开的阶数。吸声系数α可以表示为式(9):
α=1-R2-T2
(9)
数值结果表明,这种基于局部共振机理和耦合共振思想的新型超材料(图4),由于散射体间的耦合共振,M-LRAMs可以使带隙变宽并产生多个带隙,因此M-LRAMs在水下吸声方面比传统的局域共振型超材料有明显优势。但M-LRAMs也有其局限性,一方面,吸声性能与各层厚度有密切关系,随着涂层材料厚度的增加,吸收峰向低频移动。此外,随着局部共振散射体数目的增加,耦合共振将增强,其尺寸会随之增大。另一方面,该结构受材料影响较大,散射体与不同材料的组合会削弱散射体之间的耦合共振,特别是两种材料的共振频率相差很大的情况。因此,散射体的材料应选用同一材料或共振频率相近的材料。如何寻找合适的结构和材料,还需要大量研究总结。
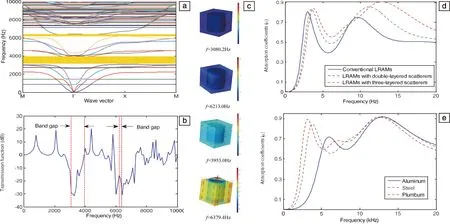
图4 具有3层局部共振散射子的LRAMs能带图和吸收系数[19]:(a)带隙,(b)透射光谱,(c)带隙下边缘和上边缘的振动模态,(d)3种LRAMs吸声性能的比较,(e)不同材料的3层散射体LRAMs吸声效果的比较Fig.4 The band diagram and absorption coefficients of the LRAMs with three-layered locally resonant scatterers[19]: (a) band gaps, (b) transmission spectrum, (c)vibration modes of lower edge and upper edge of the band gaps, (d) comparison of sound absorption of three kinds of LRAMs, (e) comparison of sound absorptions for the LRAMs with three-layered scatterers with different materials
2.3 局域共振结合优化算法的研究
除了结构形式的改变,全局优化技术可用于LRAMs的设计。基于优化的算法,如模拟退火、差分进化和遗传算法(GA)等,已经作为传统优化技术[21]的创新替代品被提出。遗传算法曾被用于解决水下材料的声传递和吸收优化问题。在这些文献中,宽频带和单频目标函数被用于涂层优化。在LRAMs的水下吸声特性的优化上,Meng等[15]采用遗传算法和一般的非线性约束算法(随机遍历选择、多点交叉和高斯变异等遗传算子),对一种多层声学超材料板进行了低频水下吸声的优化设计。遗传算法是近几十年来流行的一种全局优化方法,采用遗传算法一般能快速找到一个接近最优解的方案[22]。
单个单元可以由图5f中的虚线框架来描述,其中包含两种z方向上的局部共振单元。
理论和实验结果均表明,优化后的超材料板可以实现对水下声波的宽带(800~2500 Hz)吸收,这对消声涂料的设计具有一定的指导意义。
(10)
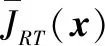
x=[ρhEhσhμhρ1E1σ1μ1ρ2E2σ2μ2r1r2R1R2]
(11)
式中,下标h表示宿主的参数:密度(ρh, 900~1100 kg/m3),杨氏模量(Eh,10~400 MPa),泊松比(δh,0.45~0.498),损耗系数(μh,0.1~1)。下标1和2表示两种局部谐振单元,和它们的参数的极限是相同的:密度(ρ1,ρ2,1000~1300 kg/m3),杨氏模量(E1,E2,0.1~10 MPa),泊松比(δ1,δ2, 0.43~0.49),损失因素(μ1,μ2, 0.1~0.3),核心半径(r1,r2, 1~7 mm),软涂层的外半径(R1,R2, 1~7.5 mm)。由于晶格常数固定,涂层的厚度等于晶格常数的两倍,即34 mm。平均密度的预赋值为2300 kg/m3。
为了验证AFC的有效性,Meng等还用经典适应度准则(CFC)[24]对上述物理模型进行了优化:
(12)
在初始种群和参数搜索空间相同的情况下,计算到了120代。图5e为两种不同适应度准则下的优化结果,纵轴为各频率吸收系数的最大值,x轴为代数。图5e中的实线为AFC的优化结果,虚线为CFC的优化结果。可以发现,在实心曲线上,吸收系数总和收敛较快,在80代后达到最大值。但虚线的强度较低,在120代内没有收敛。两个结果比较表明,遗传算法利用AFC快速搜索收敛的最优解。因此,采用AFC进行遗传算法优化LRAM平板水下吸声是可行的,且效率更高。
由表1可以发现,所有最优值都在搜索空间范围内,可以识别出两种不同尺寸的软橡胶涂层硬芯。通过遗传算法优化得到的吸收系数随频率的变化如图5g所示,也进一步验证了声学超材料中不同局部共振单元结合在水下吸声中的优势[7]。文献[7]中的计算模型是由嵌有相同散射体的两层均匀的局部共振板组成,模型的整体厚度为55 mm,与最佳涂层不同。考虑到厚度的缩放效果,频率Ω是按单元(ω/c)等比例缩小的,ω是角频率,c是声音在空气中的速度(340 m/s),L是涂层的厚度。
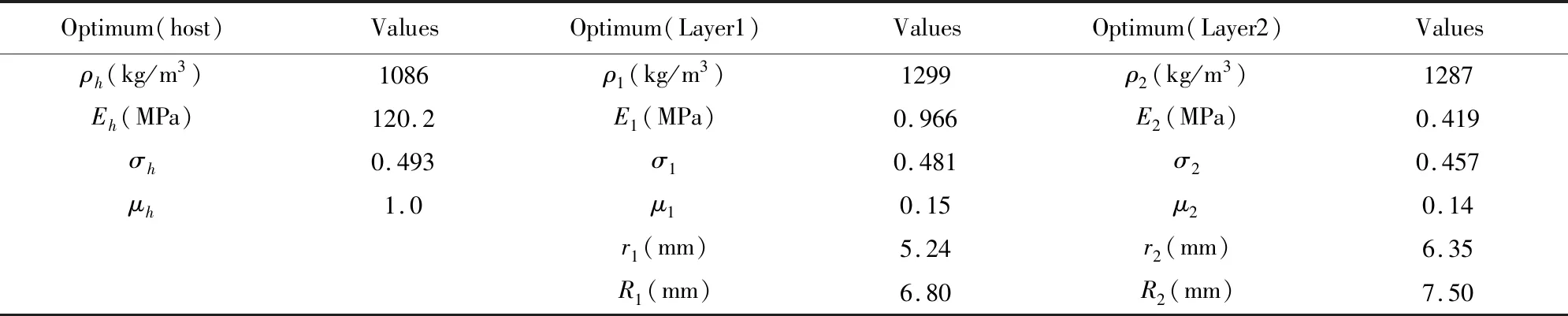
表1 橡胶涂层的物理参数(LRAM板的优化参数)Table 1 Physical parameters of rubber coating(Optimal parameters for the LRAM slab)
由图5g可以看出,在参考模型中,吸收谱中只有在Ω=0.36附近出现一个吸收峰,这是由谐振引起的两个相同的散射。可以看出,吸收系数在吸收峰后急剧衰减,有效吸收带(吸收大于0.7)出现在Ω=0.30~0.46的范围内。而从优化结果很容易发现,在Ω=0.31 (990 Hz)和Ω= 0.60 (1950 Hz)附近存在吸收峰,这两个吸收峰是由两种不同散射体的局域共振引起的。Ω=0.25~0.81波段的吸声系数均大于0.7,说明两个吸收峰的作用使有效吸声波段变宽。研究还表明,优化后的超材料板可以为水下低频吸声提供更宽的频带。
为了研究局域超材料的吸声机理,计算了在吸收谱的两个峰值频率下,zOx横截面上单个单元的位移轮廓。图5a~5d为沿正z轴运动极限的两个吸收峰的位移轮廓,其中图5a和5b为第1个吸收峰(990 Hz)的运动,图5c和5d为第2个吸收峰(1950 Hz)的运动。 图5a和5c用箭头表示位移等值线,箭头的长度缩放到位移幅值,表示zOx横截面平面上各节点的位移方向,图5b和5d给出了相应的位移幅值等值线。
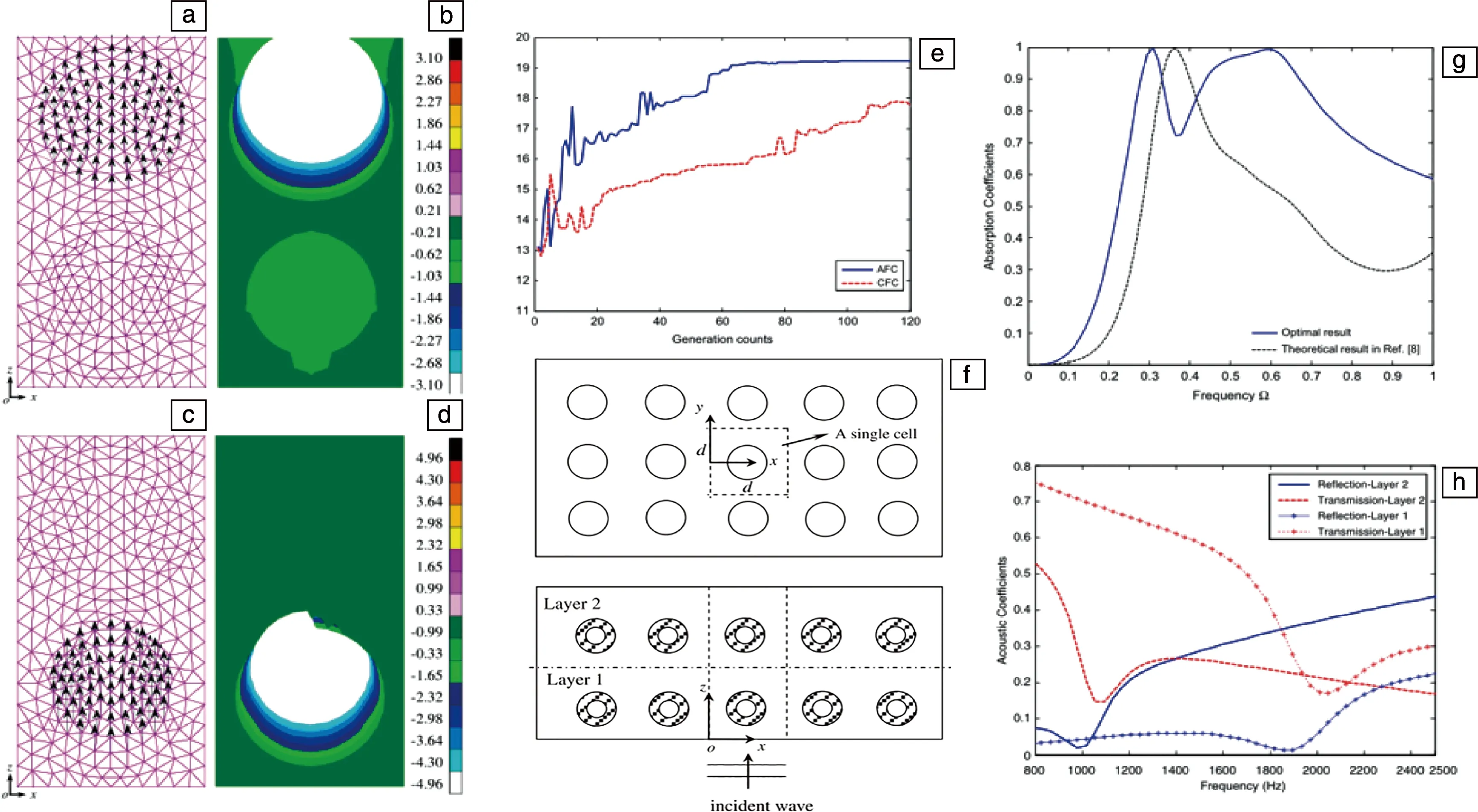
图5 在第1个吸收峰(a,b)和第2个吸收峰(c,d)的频率下,zOx截面上的单元格的总位移(×10-10 m)等值线,图5a和5c中的箭头表示zOx截面上节点的位移向量;两种遗传算法AFC和CFC的最优结果(e);LRAM平板的顶部和横截面视图(f);LRAM平板的吸收系数作为频率的函数(g);第1层和第2层的声学系数(h)[15]Fig.5 Total displacement (×10-10 m) contours of a unit cell on the zOx cross section at the frequency of the 1st absorption peak (a, b) and the 2nd absorption peak (c, d), the arrows in Fig.5a and Fig.5c denote the displacement vectors of the nodes on the zOx cross section;comparison of the optimal results by GA with AFC and CFC (e); the top and cross section views of the LRAM slab (f); absorption coefficients of the LRAM slab as functions of frequency (g); acoustic coefficients of the Layer 1 and Layer 2 (h)[15]
在图5a和5b中,振动主要局限于第2层的核心,对于振幅相等的节点,核心作为刚体振荡。由此可以推断出第1个吸收峰是由埋在第2层的散射体的振动引起的。类似的情况如图5c和5d所示,即第2个吸收峰是由嵌在第1层中的散射体的振荡引起的。可以发现芯体的位移矢量沿z轴方向,表示散射体沿入射波方向纵向振动。在吸收峰的频率处,这种局部共振单元的运动可以看作是一个质点-弹簧系统,刚性核心提供质量,软涂层起弹簧的作用。根据文献[25]中的近似方法,两种散射体的局部共振频率分别在979和1991 Hz左右,与吸收峰的频率有很好的一致性。因此,可以得出吸收峰光谱是由入射波激发的单元的共振引起的。当散射体共振时,芯体的运动引起涂层的剪切变形,使入射纵波转变为横波。横向波在粘弹性介质中很容易消散,增强了超材料板在局部共振频率范围内的吸收能力。从图5a~5d可以看出,在各吸收峰频率下,只有一种局部共振单元相对于平板其他部分具有较大的振幅。这一现象表明,每一个平板作为一个几乎独立的单位在其相应的共振频率振荡。而宿主内的振荡幅度要小得多,这意味着不同散射体之间的影响较弱。因此,有可能通过结合几个不同共振频率的LRAM板来生产宽带吸声材料。
还可以发现具有较高谐振频率的散射体排列在靠近表面的第1层,靠近波入射面,另一种类型的散射体嵌在第2层。对比表1中两种软橡胶涂层的物理参数,计算得到第1层和第2层软橡胶的纵波速度分别为82.6和37.6 m/s。虽然两种软橡胶的声阻抗都与主机的声阻抗不匹配,但两者的声阻抗相差很大,第一层软橡胶与主机的匹配度相对较好。因此,最优结果的排列可以实现过渡阻抗,从而使入射波尽可能多地撞击超材料板。为了进一步验证,计算了只有第1层和第2层浸在水中时的反射和透射系数。上述两个声学系数在一定程度上代表了介质之间的阻抗匹配条件。第1层和第2层的声学系数随频率的变化如图5h所示。比较图5h中反射系数的两条曲线,可以发现第1层在高频处具有较低的反射,这说明入射波的频率较高,比入射波从水中更容易进入第1层。从透射曲线来看,在低频处,第1层比第2层有更大的振级,说明在第1层中有更多的低频入射波在后面进入介质,这些波不能完全消散。由于第1层在低频范围具有较高的透过率,而在高频范围反射较少,因此更适合布置在靠近水面的位置。一方面,由于第1层的低频透射率较高,从第1层发射的入射波传播到第2层并最终被吸收。另一方面,高频入射波由于反射较少而直接撞击到第1层,并被散射体的共振所耗散。
基于上述研究,Meng等设计的这种基于多层LRAM的宽带吸声板,在相应的共振频率下,板的每一层都作为一个近似独立的单元振荡。采用遗传算法和一般非线性约束算法对LRAM平板在低频范围内的物理和结构参数进行优化。理论和实验结果表明,宽带吸声器的吸声性能优于只含一种局部共振散射体的吸声器。此结构将不同共振频率的LRAM层组合以达成宽频带吸声。为了在较低和更宽的频率范围内吸声,需要优化更多的参数,如晶格常数、每层厚度、局部共振散射体的形状等,涉及因素以及数据量杂多,这也是需要改进的地方。
3 水下固-液声学超晶格人工复合结构低频禁止效应研究(二极管/开关)
声波或弹性波在复合材料结构中的传播,因其在声波传播中的重要地位和在现代声学技术中的巨大应用潜力而备受关注。水下声学结构的一个研究难点在于如何实现小型化,而一维声子晶体结构具有设计简单、可以实现亚波长尺度下设计等特点,当声波透过其周期性结构后可以产生带隙,并且带隙的特征与入射角度[26, 27]以及周期性结构的材料声速[28]有关,非常适合水下声学结构的设计。
声波由流体入射固体,会发生声模转换,固体的横波声速和流体的纵波声速的相对大小会决定声波在液固传播中的模式转换问题,张赛等[29]对声波全向入射一维流固声子晶体的透射特性进行了比较研究。如图6a,声波从第一层到第N层的传播过程可描述为:
(13)
其中,φ1i和φ4i为入射波幅度,φ1r和φ4r为反射波幅度,T1,N=T1T2…TN表示声子晶体的第一层到第N层的传递矩阵。透射系数和反射系数[30]可定义为T=1/|T11|2,R=1-T。
上述方法的透射谱如图6b所示,其对角度的选择性,可以形成带隙。根据斯奈尔定律,入射声波以兰姆波的形式通过一个宽角度的板进行传播[31-33]。在实际应用中,液固结构具有如易于制造等优点,利用漏兰姆波在液固超晶格中的散射特性,可以实现超广角传播。在此基础上,研究了液体固相超晶格的全向传播,并探讨了超广角传播现象[34]。
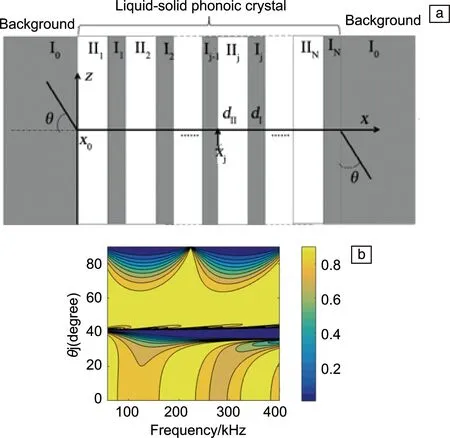
图6 有限周期一维流固声子晶体全向入射示意图(a)[29],周期为N=5“石英玻璃-水”超晶格全向透射谱(b)Fig.6 Diagram of finite periodic 1D liquid-solid phononic crystal at omnidirectional incidence(a)[29], the period is N=5 “quartz glass-water” omnidirectional transmission spectrum of superlattice (b)
图7a和7b显示了入射角对频率为376.5 kHz的单色平面波传输的影响,其中点线和星分别对应于传输矩阵法和有限元法计算的传输值。声波在均匀固体材料和相同参数超晶格中的透射如图7a和7b所示。
在均匀的固体中(图7a),在斜入射角24.9°以上发现了明显的透射下降,这表明发生了全反射。而对于超晶格(图7b),在32.3°~36.3°和63.75°~64.2°范围内的两个角度在第二临界角以上表现出高效透射,对全反射没有限制。传输矩阵法的计算结果与有限元法计算结果吻合较好,表明传递矩阵的推导是有效的。
图7c~7f是利用传输矩阵法计算的频率、入射角和透射率的三维图。当入射角大于24.9°时,没有显示出带通性质。所有高透射率的相应入射角都小于第二临界角,说明了均匀材料中全反射的限制存在。然而,在图7d~7f中显示了在填充分数不同的超晶格中产生的广角传播。如图7d所示,入射角在24.9°以上的每个通带都有大的透射率;如图7e所示,当填充分数fc增加到0.5时,带隙变宽,出现了更多的兰姆波模式;随着填充分数的增加,兰姆波模态的数量越来越多,当fc大于0.95时,0型模态下降并消失。此外,还研究了固体板厚度对超晶格透射率的影响,随着平板厚度的减小,带隙变宽,兰姆波模数相应减小,但最大入射角增大,超广角传播更易实现。可见,液体-固体超晶格的超广角传播很大程度上依赖于平板厚度的参数以及厚度与晶格间距的比值。兰姆波的布拉格散射是超广角在超晶格中传播的物理机制,是控制斜入射声传输的关键因素。通过调整固体与液体的比例,可以获得超广角传播,打破了全折射的限制。液体-固体超晶格对扩大超广角传播的频率范围和入射角具有重要作用。
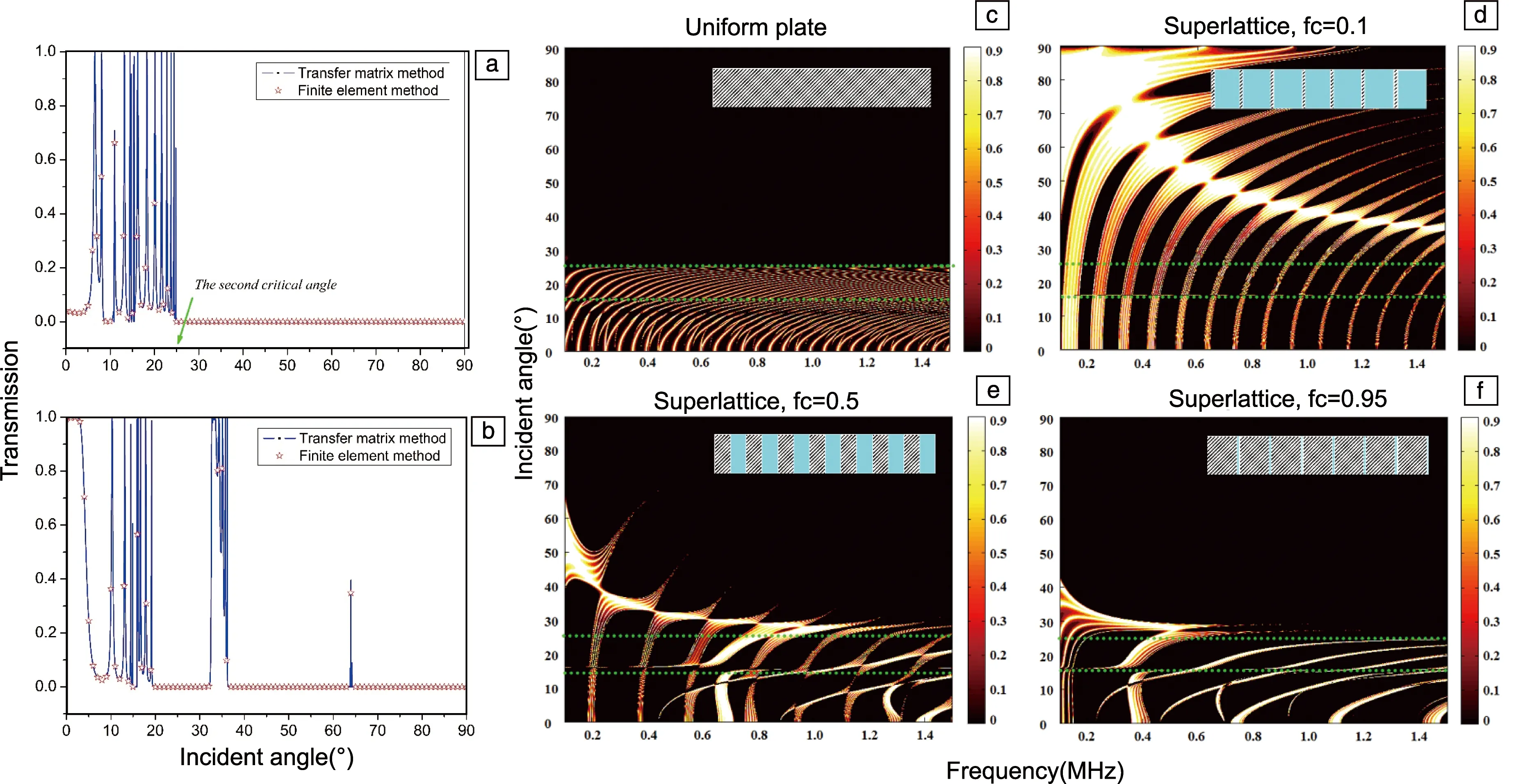
图7 通过传输矩阵法和有限元法计算的均匀板(a)和fc=0.5、N=7、f=376.5 kHz超晶格(b)中传输与入射角的关系;在均匀板(c)和N=7、fc=0.1~0.95的超晶格(d~f)中通过传输矩阵法计算的频率、入射角和透射率的函数,色谱指材料透射率,插图分别显示了均匀固体材料模型和超晶格模型[34]Fig.7 Transmissions versus incident angle, calculated by the transfer matrix method and finite element method in the uniform plate (a) and the superlattice with fc=0.5, N=7, f=376.5 kHz (b); color-scale representations of transmissions as a function of both frequency, incident angle and transmission in a uniform plate (c) and in a superlattice N=7 with fc=0.1~0.95 (d~f), the thermal bar refers to the transmission of the material, the insets show the models of the uniform solid material and the superlattice, respectively[34]
此外,利用控制变量法对角范围的变化特性进行了较为全面的研究。结果表明,填充分数、层数、波速和质量密度对夹角范围有显著影响。在此基础上,Zhang等提出了一种有效的方法来获得一个宽角度范围的低频禁带,这将有助于低频禁带效应在各种器件中的潜在应用,如低频滤波器和亚波长单向二极管[35]。不过其有效角度比较狭窄,但设计两相级联结构可以实现超宽角的低频禁带传输(图8g)[36]。这种声低频禁带材料可以在选择角度范围内制作出优良的声低频滤波器,在亚波长声学器件中具有广泛的应用价值。
Li等[37]利用二极管两端的模态跃迁构造了一个基于声子晶体的声二极管(AD)。Zhang等[38]提出了一种利用多孔超材料作为梯度指数结构的宽带非对称传输装置,这些非对称传输声子晶体受限于尺寸波长,即器件的尺寸要大于声学波长才会有多重散射,而在亚波长尺度下很难实现。由于其是基于声波在一个周期内传播时的带隙现象,因此利用这一原理无法实现单向亚波长传输。
在此基础上,Zhang等[39]设计了一个由一维超晶格作为低频禁波调节器和一个周期性矩形声栅作为波前转换器组成的结构(SAAT)(如图8a~8c)。利用液体-固体声超晶格的低频禁止传输实现了亚波长的非对称声传输。SAAT中的结构常数L和超晶格常数D分别为0.6λ和0.128λ,其中λ是波长,透射比可以达到108高整流率。这种设计突破了波长的限制,允许单向低频声波传输,这是在单向信号传输应用中集成声学设备的小型化所必需的。
4层固态流体超晶格(superlattice, SL)的亚波长传输特性如图8d所示,其中传输系数是使用传输矩阵[34]作为频率和SL入射角的函数计算的。低频禁止传输代表能量衰减,当晶格常数变得比波长小得多时,这与由布拉格散射引起的带隙(见图8d中的第一个布拉格带隙)不同。图8e和8f分别为入射角为0°和41°时,不同层数PMMA-water SL的透射系数。
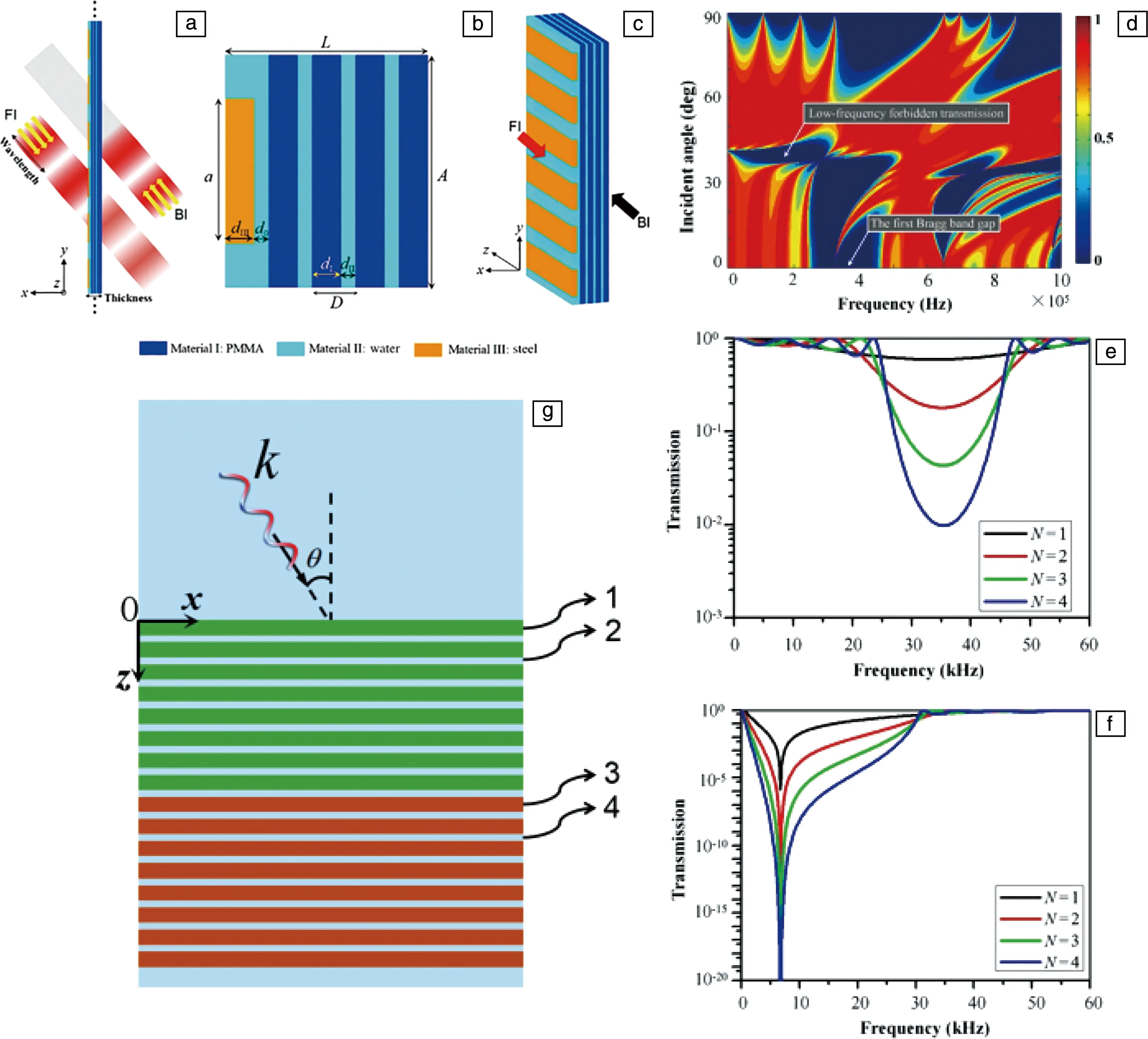
图8 SAAT装置的示意图(a);SAAT结构单位单元的示意图(b);SAAT结构的三维图解(c);4层PMMA-water SL的透射系数是频率和入射角的函数,箭头表示低频禁止透射(d);当入射角为0° (e) 和41° (f) 时,不同层PMMA-water SL的透射系数[39]; 两相级联结构示意图,由两个具有相同晶格常数D的亚固液超晶格结构(SFSLs)组成,材料1和3是两种不同的固体,材料2和4都是水(g)[36]Fig.8 Schematic illustration of the SAAT device(a); schematic of a unit cell of the SAAT structure(b); three-dimensional illustration of the SAAT structure(c); transmission coefficient as a function of frequency and incident angle of the four-layered PMMA-water SL, low-frequency forbidden transmission is indicated by the arrow(d); transmission coefficients of the PMMA-water SL with different layer when the incident angle is at 0°(e) and 41°(f)[39]; schematic of the cascade structure studied, which consists of two sub-SFSLs with the same lattice constant D, materials 1 and 3 are two different solids and materials 2 and 4 are both water(g)[36]
低频禁带传输与布拉格带隙传输的显著差异表明,低频禁带传输可以作为制作亚波长不对称声传输结构的良好选择。
该固液声波的低频禁止传输特性可用于控制声能在SAAT结构中的流动。对于入射角为41°的平面波的反向入射(BI),禁止透射。相反地,对于正向入射(FI),使用周期性排列的矩形棒组成的声光栅使波阵面进入主超晶格之前发生畸变。当衍射波的入射角度偏离41°时,会产生高透射。因此,SAAT结构导致单向亚波长响应(如图9a~9d)。
利用超声波传输技术测量声功率技术[40],验证了SAAT结构的低频禁带传输性能(图9e~9h)。
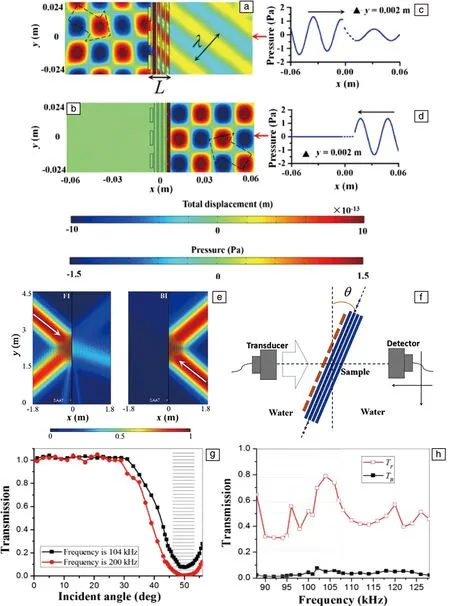
图9 频率为65 kHz时BI和FI两种情况的声压和位移分布模拟图,虚线黑色空心箭头表示传播方向(a,b);y=0.002 m时的压力分布(c,d);在FI(左)和BI(右)情况下,高斯光束通过SAAT结构的传播,白色箭头表示波的传播方向(e);实验装置示意图(f);实验测量的4层PMMA-water在104和200 kHz处的透射光谱作为入射角的函数(g);SAAT的实验透射光谱作为FI和BI的频率函数(h)[39]Fig.9 Simulated acoustic pressure and displacement distributions for the BI and FI cases at the frequency of 65 kHz, dashed black hollow arrows indicate the propagation directions(a, b);the pressure distributions at y=0.002 m(c, d);propagations of a Gaussian beam through the SAAT structure for FI (left) and BI (right) cases, white arrows indicate the wave propagation directions(e);schematic diagram of the experimental setup(f);experimentally measured transmission spectra at 104 and 200 kHz as a function of the incident angle for a four-layer PMMA-water SL(g);experimental transmission spectra of SAAT as a function of frequency for FI and BI(h)[39]
超表面薄结构是由设计的反射或透射的微结构排列在特定空间组成[41, 42]。在水下条件,超表面具有薄层的显著优势,并为薄结构的波束控制、可调谐透镜和声学隐身提供了一个有效的途径。受电子开关机理的启发,声学开关被提出通过布拉格散射或本地共振[43]来开启和关闭带隙。Babaee等[44]提出了一种用弹性变形螺旋的准声道材料来开启和关闭声波的传播。水下水声开关的研究在噪声消除、声纳探测控制和通信声波数字化等方面具有潜在的应用前景。作者[45]提出了一种用于控制波传播的超表面声开关(MAS)。该结构由声栅和双层聚甲基丙烯酸甲酯板组成,可视为水下超表面,从理论上推导了PMMA-water结构的非模态转换(如图10a~10c),用全波模拟验证了MAS的声栅的声衍射和双层PMMA禁带传输对开关机制的影响,并通过改变声栅的角度调节MAS来控制波的传播。此外,实验制作了MAS并实现了宽带作用(图10d~10g)。
该装置可用于控制水下声目标探测,也可实现二进制数字编码(图10h)。实验记录了一组开关的声音信号,将声波光栅按位序010011010100000101010011(即信息MAS)进行开关,实现声波数字化。
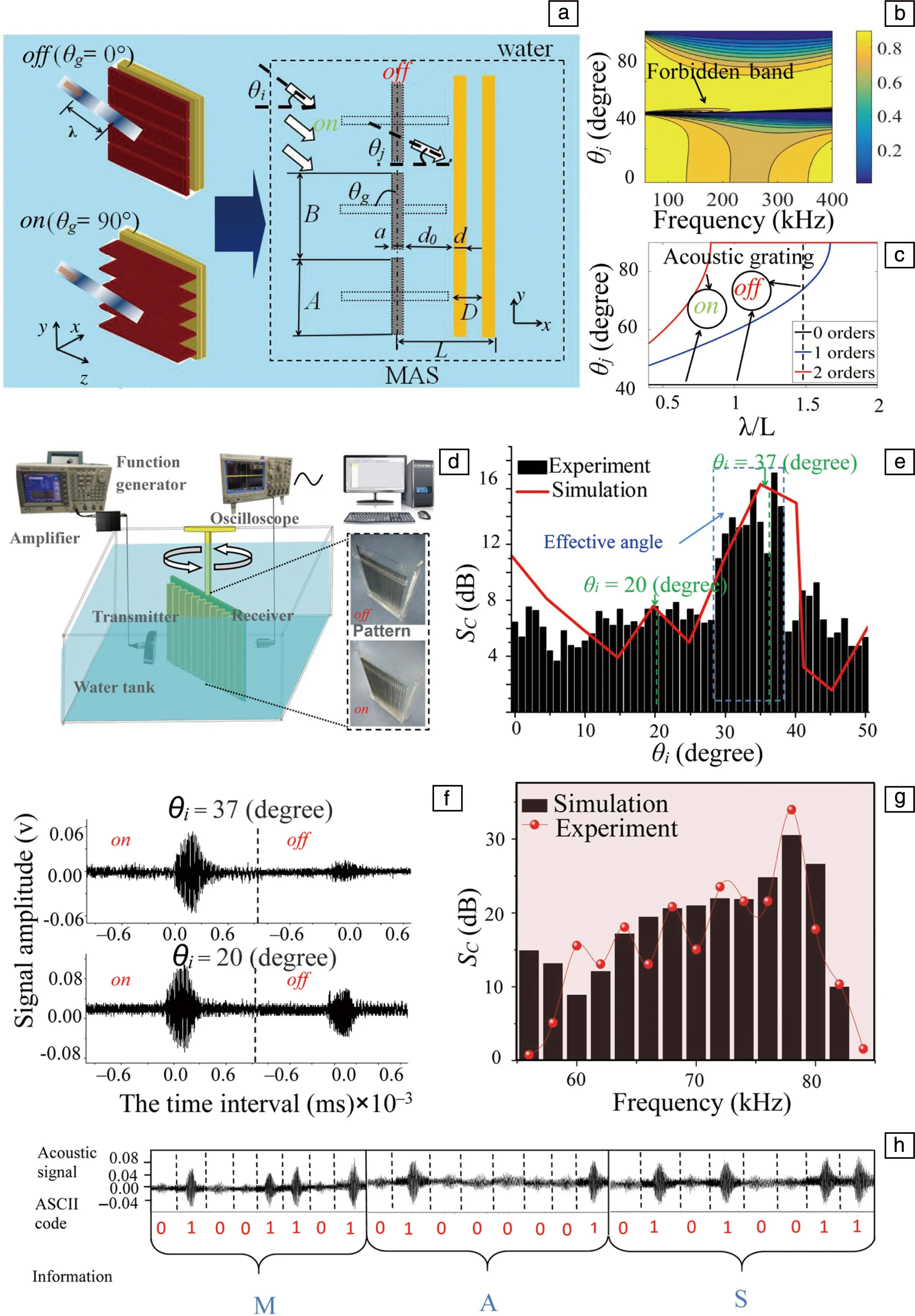
图10 水下超表面声开关:(a) 结构系统图,(b) 透射系数与频率和入射角的关系(N=2),(c) 衍射角与归一化波长的关系;声转换实验:(d)实验的系统图和MAS的开关模式,(e)在频率80 kHz下,透射比对入射角的依赖性用于实验测量和数值模拟,(f)在入射角度为37°(上)和20°(下)时MAS传输波形的比较,(g)在入射角为37°时试验测量和数值模拟的MAS的宽带切换性能,(h)将MAS声学调制成位序列“010011010100000101010011”[45]Fig.10 Underwater metasurface acoustic switcher:(a) systematic diagram of the MAS structure, (b) transmission coefficient of frequency and incident angle, where N=2, (c) relationship between diffraction angle and normalized wavelength; Acoustic switching experiments: (d) systematic diagram of the experiment and the off and on patterns of MAS, (e) dependence of transmittance on incident angle for experimental measurements and numerical simulations for frequency 80 (kHz), (f) comparison of the transmitted waveforms through MAS for incident angles θi=37°(upper) and 20°(lower), (g) broadband switching performances of MAS of experimental measurements and numerical simulations for θi=37°, (h) acoustic modulation by MAS into the bit sequence“010011010100000101010011”[45]
此外,MAS与声二极管有不同的功能。以往的研究都是利用声二极管实现单向入射方向的高透射,而在相反方向低透射[39, 46]。MAS仅通过改变声栅角来控制单方向的声传输,而不考虑反方向的声传输。特别是在off配置下,由于声栅几乎是封闭的,且禁止波的传输,MAS无法实现非对称传输。宽带MAS可作为一种薄器件用于控制噪声辐射,在器件厚度小于波长的情况下,MAS也能有效地开启和关闭水下波的传播。这种设计可提供另一类具有广泛水下应用的超表面,可用于噪声控制、声学通讯、目标探测等。
4 水下超材料其他应用研究
声学超材料的负折射、表面反常效应使其在声透镜、声发射器等方面有望取得突破性进展。Zhang等于2009年设计了基于超材料的声学超棱镜[47],可以灵活地在水中控制声波束的传播方向。随后,研究者先后提出了水声、空气声超材料的声透镜模型并实现了原理性实验验证[48]。Farhat等于2008年将声学斗篷设计理论引入到液体表面波的控制中[49],提出并通过实验验证了液体表面波隐身声斗篷的设计;2009年,他们又将该理论引入到薄板弯曲波的控制中,论证了坐标变换理论应用于弯曲波控制的可行性,推导了弯曲波斗篷的设计公式[50]。此外,中国科学院声学研究所杨军等首次制备出了水下声学隐身毯的样品(图11a)[51],其在变换声学中引入参数弱化因子,牺牲了一定的阻抗匹配,实验验证了声隐藏的功能,在未来水下反探测中具有重大应用前景。Li等[52]于2009年利用多层渐变的声学超材料设计了水声声学棱镜(图11b),该棱镜镜头由36个黄铜鳍在空气中嵌入黄铜基板组成,能将声信号中的瞬逝波分量转化为行波分量进行放大。

图11 声学隐身毯(a)[51];声学棱镜 (b)[52]Fig.11 Acoustic stealth blanket(a)[51]; Acoustic hyperlens (b)[52]
在器件小型化方面,模拟海豚生物探测器将有助于开发具有高方向性的亚波长生物发射系统,复杂的超材料几何形状和多相复合材料导致亚波长声源产生定向水下声束,作者[53]应用电子计算机断层扫描(CT)技术对江豚头部的3个主要声学要素——气囊、额隆和颅骨进行了声学参数提取,据此设计了一种用声速分布的梯度超材料模拟额隆,用空气腔模拟气囊,用钢结构模拟头骨,研究了各单元对声波束控制的影响,为开发控制水声传播的人造超材料提供了宝贵的生物启发模型。此外,这种混合超材料系统[54]具有可编程性、再现性和人工性等优点,进一步结合生物保角变换方法[55],使得人工结构的参数化声速可以根据需要进行调整,以操纵声学功能,为水下亚波长声纳、医学超声等声学应用提供参考。
5 结 语
在空气中对电磁力声光热等领域超材料的研究比较多,但在水下,由于影响因素比较复杂,光电等信号在水下衰减大,而声波在水下受影响较小,声模转换效率也比较高,故水下声学研究很重要。
本文较系统地介绍了国内外水声超材料的研究进展,空气中传统的声学局域共振型超材料在水下研究时,涉及到流固耦合效果不佳等问题,研究者通过结构以及理论算法等方面的创新,基本解决了局域共振型超材料在水下不适用的问题,并且初步实现了宽带作用。但水声超材料的缺点同样明显,结构复杂、耦合共振受材料和波长尺寸影响较大,这些都制约着水下超材料的声学应用。对复合型超材料透反射调谐机制的研究,打破了布拉格散射的限制,为水下超材料小型化提供了思路。应用方面,声学开关、基于变换声学的隐身地毯超材料、水下仿生探测器等的提出,都可以证明水声超材料在水下吸隔声的吸声器设计、噪声控制、声学通讯、目标探测等领域具有十分重要的意义。
水声超材料无论在基础理论还是工业技术方面都具有巨大的发展空间,而多方面的探索和融合发展将有效推进水下声学研究领域的发展。
