声学超构材料技术实用化的进展
2021-03-17黄唯纯钟雨豪解龙翔颜学俊卢明辉陈延峰
刘 乐,黄唯纯,钟雨豪,赵 涵,解龙翔,颜学俊,卢明辉,陈延峰
(1.南京大学材料科学与工程系固体微结构物理国家重点实验室 现代工程与应用科学学院,江苏 南京 210093)(2.南京大学 人工微结构科学与技术协同创新中心, 江苏 南京 210093)
1 前 言
声学是研究声波在不同介质中传播的物理现象的科学,是物理学的一个重要分支。声学的应用几乎存在于现代社会的各个方面(如图1[1]),在工程科学、生命科学、地球科学和人文艺术方面尤为重要。对声波进行调控的一切手段,包括主动和被动控制,都需要通过声学介质得以实现。因此,声学材料是声学研究中必不可少的一部分,特别地,要想实现对声波激发、传播、调制、转换和输出的调控,必须依赖于人们对材料声学的深刻认识,以及按需设计和制备声学材料的技术进步。虽然关于声波在常规介质中的传播规律早在19世纪末已有基本定论,但类比于电子能带理论,人们发现可以利用周期性材料中声波的能带结构实现对声波传播的调控[2],相应地,可以通过构造人工结构来调控经典波的传输。自20世纪90年代以后,通过人工设计的微结构材料对声波的能带结构进行设计剪裁,探索和发现新的声学效应、材料和器件,逐步成为一个热门的研究领域——声学超构材料。
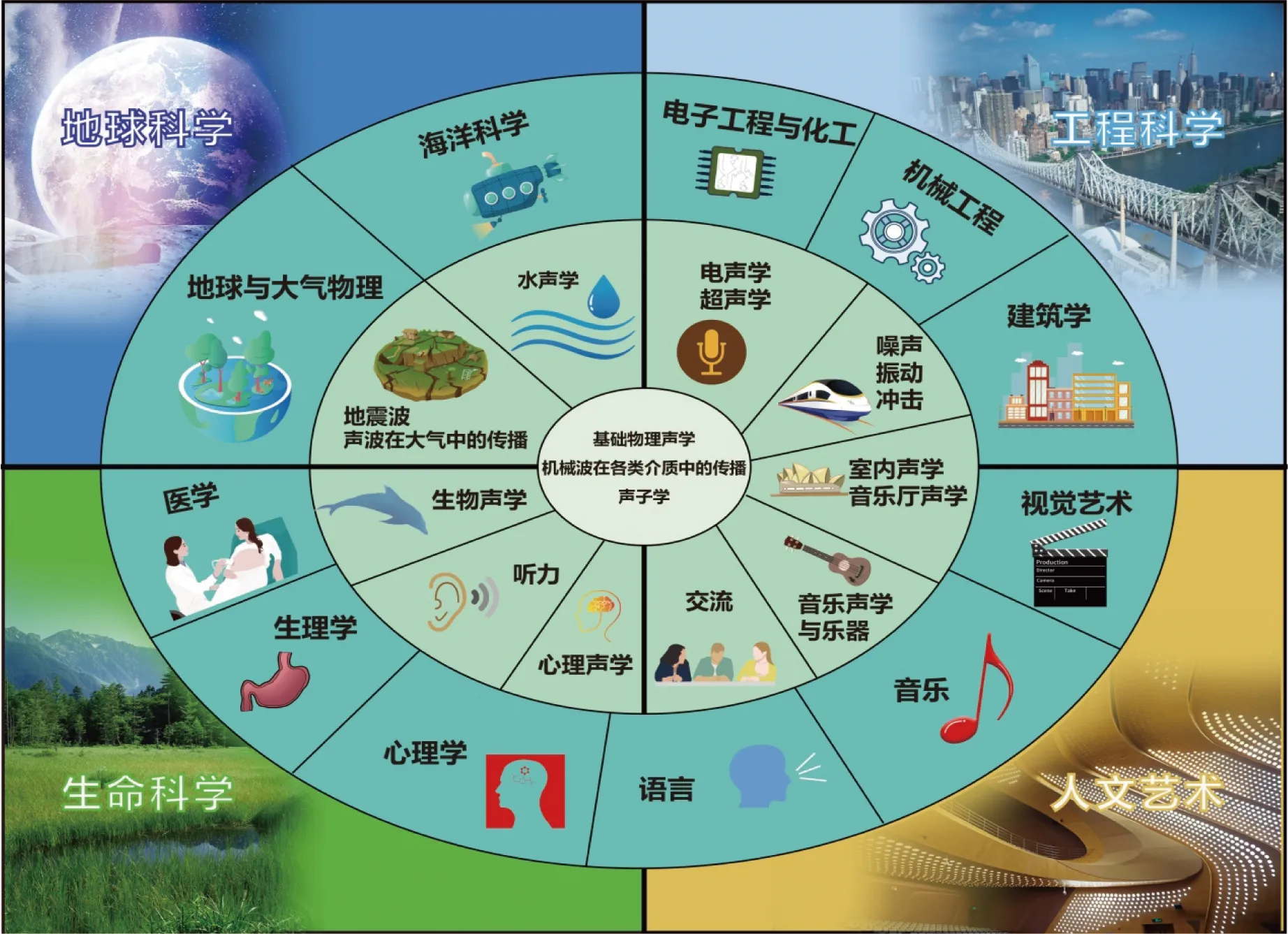
图1 声学学科环状图[1]Fig.1 Acoustics discipline diagram[1]
1.1 声学超构材料的历史
作为一种人工结构,超构材料往往由多个结构单元组成,整体上表现为具备不寻常的等效参数的连续介质材料。利用周期性结构调控波的传播行为在几十年前的固体物理中就已有研究,然而关于利用工程结构调控经典波传播特性的研究是从光子晶体[3-5]和声子晶体[6]开始。广义上第一个声学超构材料是2000年香港科技大学的刘正猷等利用硅橡胶铅球实现深度亚波长的局域共振[7],由于亚波长这一特性使得局域共振型超构材料受到了研究人员的高度重视。基于此项工作,以及受到光学、电磁学相关工作的启发,研究人员致力于利用声学超构材料对声波传播的特殊控制来实现自然界不具备的声学参数,例如声波的负折射[8, 9]、亚波长成像[10]、声学“隐身斗篷”[11, 12]、逆多普勒效应[13, 14]、单向传输[15, 16]、声完美吸收[17, 18]等等。
1.2 声学超构材料研究现状
声学超构材料可以定义为:通过对材料在特征物理尺度上进行一定序构设计,使其获得常规材料所不具备的超常声学性能的一种人工设计制造而成、具有特定结构的复合材料。
当前,声学超构材料的研究,基本形成了以功能基元序构[19]为设计理念,以多重散射理论[20]、平面波展开理论[21]等为理论方法,以等效介质理论[22]为主要评价方法的物理思想和方法论体系。同时,声学超构材料所带来的新物理思想也在悄然改变传统声学多孔材料的研究,超结构杂化声学多孔材料的研究也逐渐普及。在设计层面,随着基础理论的深化和研究实践的不断展开,研究人员已经基本归纳概括了针对特定声学功能的超构材料功能基元的基本类型与序构的基本形式,在此基础上给出了相应的解析与数值模型,为进一步引入人工智能和机器学习计算指导超构材料结构设计打下了基础[23]。
近20年来,随着增材制造技术的发展,声学超构材料的实验室加工与制备所面临的困难逐步得到解决。而在测量手段层面,适应声学超构材料特殊需求的测量手段和仪器也得到了长足发展。以阻抗管[24-27]、小容积声学混响测试系统[28, 29]、热线矢量传感器[30]为代表的一类仪器逐渐由工业领域走入科学研究领域。中小型样件的制备与测试体系基本构建完成,为下一步产业化发展打牢了研发基础。
1.3 声学超构材料应用面临的困难
在应用层面,声学超构材料仍然面临许多亟待解决的困难。作者认为主要可以归纳为以下3方面。
首先是生产工艺问题。新材料的工程应用首先要解决的是大批量生产的工艺问题。而当下的声学超构材料研究以实验室规模的加工为主,如3D打印,基本没有以超构材料工业化批量加工为目标的工程应用类研究。很多研究在设计阶段就没有考虑大批量应用的前景,也没有为传统加工工艺留下设计余量,乃至产生了一批甚至无法使用现有最先进的增材制造技术制备的超构材料设计[31]。在现有工业技术基础上,研发或改造出适用于声学超构材料批量生产的专门技术是一个亟待开展的工程科学研究方向。
其次是声学超构材料使用的理念与现实的错位。在科学研究中,科研人员总是在强调直接、单独使用超构材料,强调声学超构材料宽频带的设计方法问题,然而工程实践中往往需要综合使用多种声学材料。超构材料应该有针对性地实现工程中的极限声学性能,这可能是其应用的突破口。声学超构材料与传统声学多孔材料的结合[16, 32-34]、声学超构材料与主动控制手段的结合[3, 35-38]等面向应用的工程科学课题都亟待开启。
最终落实到应用层面,最大的困难还是成本问题。目前,声学超构材料的生产与研发成本居高不下,以吸声超构材料为例,超构材料单价是具备类似功能的多孔材料的五到十倍。高成本一部分是由于在工艺设计和使用指导思想上的偏差,另一部分在于声学超构材料主要面向诸如低频、超薄、场调控等极限功能[39-42]的实现,而适用于此类功能的基础材料成本较高,这往往是新材料普遍面临的问题。
本文将简要介绍实用型声学超构材料设计、表征与测试手段的进展,并展望了其应用前景。首先介绍几种面向不同应用场景的实用型声学超构材料,从理论和现象的角度简要概括这些材料所依据的物理思想与设计方法,着重介绍其应用前景与潜力,最后展望实用型声学超构材料在近期的应用实例与应用前景。
2 实用型声学超构材料研究进展
2.1 吸声超构材料
在各类声学材料中,需求最大的是面向减振降噪工程的吸声材料。传统吸声材料主要基于多孔材料和微穿孔板,其中多孔材料[43]在中高频段可以实现良好的吸声性能,随着频率的降低,需要材料体积显著增加;微穿孔板[44]则是通过调节背板后的空腔的体积,可以在某个需要的频率范围实现良好的吸收效果,然而由于共振的特点,微穿孔板的工作频带往往过窄难以应用。近年来兴起的超构材料可以在较小的体积下,通过对声学材料的结构设计,利用亚波长局域共振原理,实现在较宽频率范围内的高效吸声。在局域共振条件下,与传统材料质量密度和体积模量均为正值的情况不同,超构材料的质量密度与体积、弹性模量会表现出很强的色散,在共振频率附近甚至等效为负值。
大部分吸声器主要基于共振将声能转化为热能的机制,因此需要对声波在结构中传播的损失做出精确的描述。Stinson[45]基于基尔霍夫理论的近似解,在一定范围内将声传播中的热效应与粘滞效应分离开,可以描述声波在任意截面管道中传播的损失。Peng等[46]设计了一种复合蜂窝三明治面板结构,可以在600~1000 Hz实现90%的吸声性能,并构造了亥姆霍兹谐振器和微穿孔板两种解析模型来计算这种三明治面板的吸声性能。 Jiménez等[47]通过耦合多个亥姆霍兹共鸣器设计了宽频的、不对称的声吸收器,该共鸣器阵列通过级联效应,实现了300~1000 Hz的良好吸声,同时结构仅为波长的十分之一。图2a中左上图是单个的亚波长吸声单元模块,由两个亥姆霍兹器构成,可以在300 Hz处实现声波的完美吸收,右上图则是将亥姆霍兹单元模块拓展到8个,通过设定相应的代价函数进行优化得出。为更进一步了解散射问题的物理意义,可以分析图2b中复频率面中散射矩阵的本征值与本征矢量,值得注意的是,完美吸收仅限散射矩阵本征值为0的点落在频率的实轴处。
利用单元之间的耦合,可以有效地拓宽吸收器有效工作频率范围。进一步地,为获得一个“最优”的谐振器, Yang等[48]考虑到声学中吸收频率范围和材料厚度关系,得出了基于因果律的不等式,从而指出特定厚度的材料吸声频带所能达到的极限。此外,还指出低频的声吸收需要更大的材料厚度,以及在窄频带内实现吸声系数近1是完全可行的。基于这一原理约束,研究者提出一种基于目标频带范围设计原理约束下最薄结构厚度的概念。如图2c,这种超构材料由16个法布里-珀罗谐振器组成,通过折叠空间,可以进一步减少结构厚度,在结构表面增加一层海绵可以有效减少倏逝波的影响,从而减少表面阻抗在频谱内的振荡,实现良好的宽频吸声。
除了上述基于法布里-珀罗谐振器的结构外,Huang等[49]提出一种变形的亥姆霍兹器(图2d),这种结构可以进一步减小共鸣器的厚度,在吸声效果改变不大的情况下显著减少其厚度。结果还显示,吸收峰的频率与其质量因子成反比,吸收峰频率越低,其质量因子越高。同时基于这种共鸣器结构,研究者[50]也提出了一种弱吸声单元耦合的轻薄宽带结构(见图2d右图),调控原先一系列弱吸声单元之间的耦合作用,可以显著提升整体在宽频范围内的吸声性能。

图2 耦合多个亥姆霍兹共鸣腔的宽频声吸收器(a),对应吸收器的复频率面(b)[47];16个法布里-珀罗谐振器组成的吸声结构(c)[48];嵌入颈部长管的亥姆霍兹谐振器的弱吸收耦合(d)[49]Fig.2 Broadband acoustic absorber coupled with multiple Helmholtz resonators(a), complex frequency of the absorber(b)[47]; Sound-absorbing structure composed of 16 Fabry-Perot resonators(c)[48]; Coupled weak resonance of Helmholtz resonator embedded apertures(d)[49]
Liu等[51]提出一种具有多阶声吸收的超构表面,如图3所示,该超构表面在450~1360 Hz具有连续的近完美吸收,其单元是一种穿孔的复合的亥姆霍兹谐振器,多峰的现象是因为带有隔板的多自由度系统引起的,可以通过等效的声学电路进行解释。
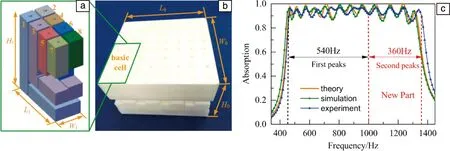
图3 超表面结构单元示意图,共有8个单元(a);对应的超表面样品(b);超表面的理论、仿真、实验吸声系数曲线,共有12个近完美吸收峰(c)[51]Fig.3 Schematic of the metasurface’s cell consisted with eight detuned units (a); The sample of the metasurface, respectively(b); The theoretical, simulated and measured absorption coefficients curve of the metasurface, which is comprised of twelve near-perfect absorption peaks (c)[51]
在经典的单一等效介质的超构材料研究之外,科研人员综合利用传统声学多孔材料制备了杂化超构材料[52-55],其中声能被约束并耗散在具有复杂几何结构的谐振器中,包括具有刚性隔板或矩形不规则结构的多孔层(如楔形设计、双孔介质等)、多孔亥姆霍兹共振器以及具有不同层厚、纤维直径和孔隙率的金属纤维材料等。与前述的声学超构材料不同,多孔杂化型超构材料克服了如薄膜型谐振器[56]和迷宫型超构材料[57]等带宽较窄的缺点。多孔材料的存在,增加了能量的消耗,并在实际应用中拓宽了工作频率范围。几种多孔杂化型声学超构材料在亚波长尺度显示了出色的吸声系数,例如具有刚性周期性矩形不规则结构的多孔材料[16]、有刚性分隔壁和内谐振器的多孔材料[58]、不同纤维直径和孔隙率的金属基多孔材料[33]。
Ji等[34]构造了一种倒楔形的平面型多孔声学超构材料(图4),这种多孔超构材料基于三聚氰胺泡沫,可以实现异常反射的现象。与传统的连续的三聚氰胺泡沫和等质量的倒楔形吸声器相比,这种多孔杂化型超构材料的吸声曲线具有更宽的频率范围和更大的入射角度范围。
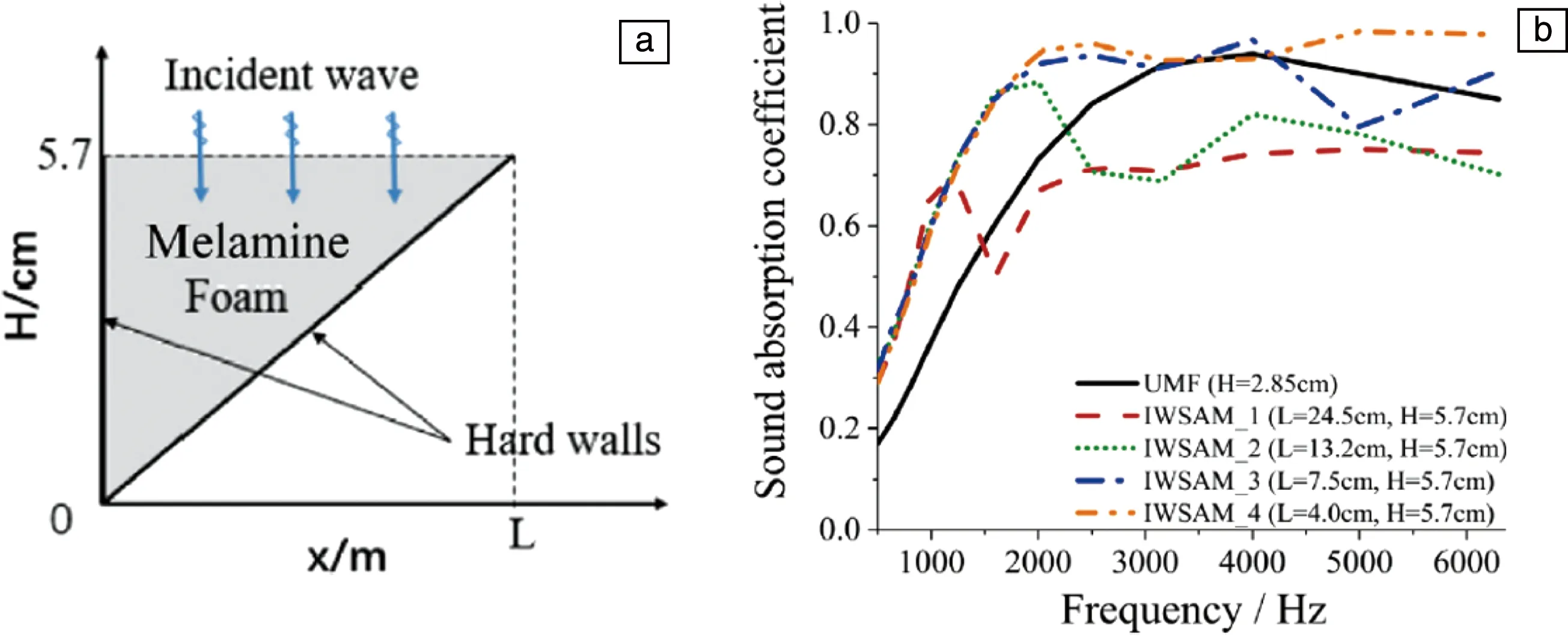
图4 倒楔形的平面型多孔声学超材料结构示意图(a);1/3倍频程下的吸声系数(b)[34]Fig.4 Schematic of plane type porous acoustic metamaterial with an inverted wedge shape (a); Sound absorption coefficient in 1/3 octave band (b)[34]
实际应用中,多孔声学超材料仍然存在许多挑战。由于结构尺寸、声学性能、成本和耐久性的限制,大多数声学超构材料未必适合于实际应用,需要新的设计和制造技术来达到性能与成本的平衡。多孔声学超材料设计还需要考虑温度梯度、外部流动等对结构和材料性能的影响。
2.2 隔声超构材料
声学材料的轻量化是实际应用中的一大需求,但是受质量定律限制,轻质材料的声传递损失很低,尤其是对低频声波而言。传统的隔声材料在高频阶段具有良好的隔声性能,但在低频阶段其隔声性能急剧下降。因此,同时满足高刚度、轻量化,并且具有良好隔声性能的超构材料是近几年的研究热点。
薄膜型超构材料因为具备轻量化、低频隔声性能好的潜在可能而引人关注。Yang等[59]首先提出薄膜型低频隔声超构材料。通过将一个小质量块附着于具有固定边界的薄膜上,在前两个共振频率间调试窄带的负动态有效质量,可以实现声学上的全反射,堆叠多个薄膜板可以拓宽频率带宽,在一定程度上实现宽频隔声。
Sui等[60]将蜂窝结构与不含质量块的薄膜结合,设计了一种蜂窝型声学超材料。将各向同性的薄膜粘在蜂窝结构顶部(图5a~5c),该结构对500 Hz以下声波的传递损耗均超过25 dB(图5d),同时,面密度仅1.3 kg/m2。此外,以蜂窝结构超材料为核心的夹心板在低频下产生的声学传递损失始终大于30 dB。

图5 一个蜂窝单元(a),蜂窝单元侧视图(b),蜂窝型声学超构材料示意图(c),传递损耗的实验/模拟结果(d)[60]Fig.5 Unit cell of honeycomb acoustic metamaterial (a), side view of the unit cell (b), prototype of the metamaterial (c), experimental and simulation sound transmission loss results (d)[60]
Ma等[61]将协同行为引入超材料设计当中,考虑系统的密集共振模式和多单元的协同耦合行为,通过9个谐振器组成的平板结构,实现剧烈的宽带声衰减,低于2000 Hz范围内的平均声传递损失高于40 dB。这种协同设计的理念可以为宽频带的声衰减提供新的自由度。目前超材料用于隔声领域主要的挑战是大尺寸结构下的隔声,然而,现有的研究工作主要集中在具有固定边界的小型单元的声传输损耗(sound transmission loss, STL)上,从而导致其隔音性能与工程应用中使用的大型结构的差异很大。Wang等[62]对大尺寸的薄板型声学超材料(plate-type acoustic matamaterials, PAMM)进行数值研究(图6),结果表明,通过在面板上负载适当的质量可以实现多单元协同的宽带隔声效果,在300~900 Hz具有平均STL高于20 dB的宽频带隔声效果。
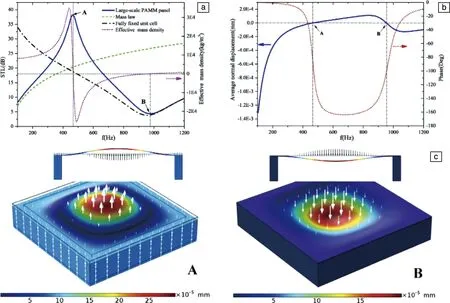
图6 大尺寸薄板型声学超构材料面板的有限元分析结果[62]:(a)声传输损失(STL)和等效质量密度,(b)平均法向位移和相位,(c)A点STL峰值和B点STL低谷时的振动情况Fig.6 The finite element analysis results for a large-scale plate-type acoustic metamaterials panel[62]:(a)the STL and effective mass density, (b)the average normal displacement and phase, (c)the vibrational profiles of point-A (STL peak) and point-B (STL dip)
传统声学屏障在隔声的同时也阻碍了空气的流动。在实际的生活中,一些场景需要在消除噪声的同时保证空气流动顺畅。以往,在设计隔音但又能保证空气流动的屏障时,通常是设计一条带有吸收性衬里或穿孔隔板的曲折气流路径。而实际上,更弯曲的路径有利于更充分的降噪,继而带来更大的压降,导致较差的通风效果。基于类法诺共振的超构材料可以在保证隔声效果的同时具有良好的通风效果,然而这种局域共振只能在狭窄的相消干涉频率附近工作[40]。Sun等[63]设计了一种平面式亚波长厚度的宽频通风的声学屏障,如图7a所示,一个隔声单元是由中央通孔和两组环绕的螺旋叶片组成,中央通孔保证了气流的充分流通,螺旋叶片保证了在所需频域内具有丰富可调的单极和偶极模式表面响应,从而实现声能的高衰减。该结构良好的隔声效果是由于等强度单极子与偶极子响应的叠加。此研究解决了现有超材料窄带降噪的局限,同时具有很好的通风性,为绿色建筑的天然通风和降噪提供了可能。
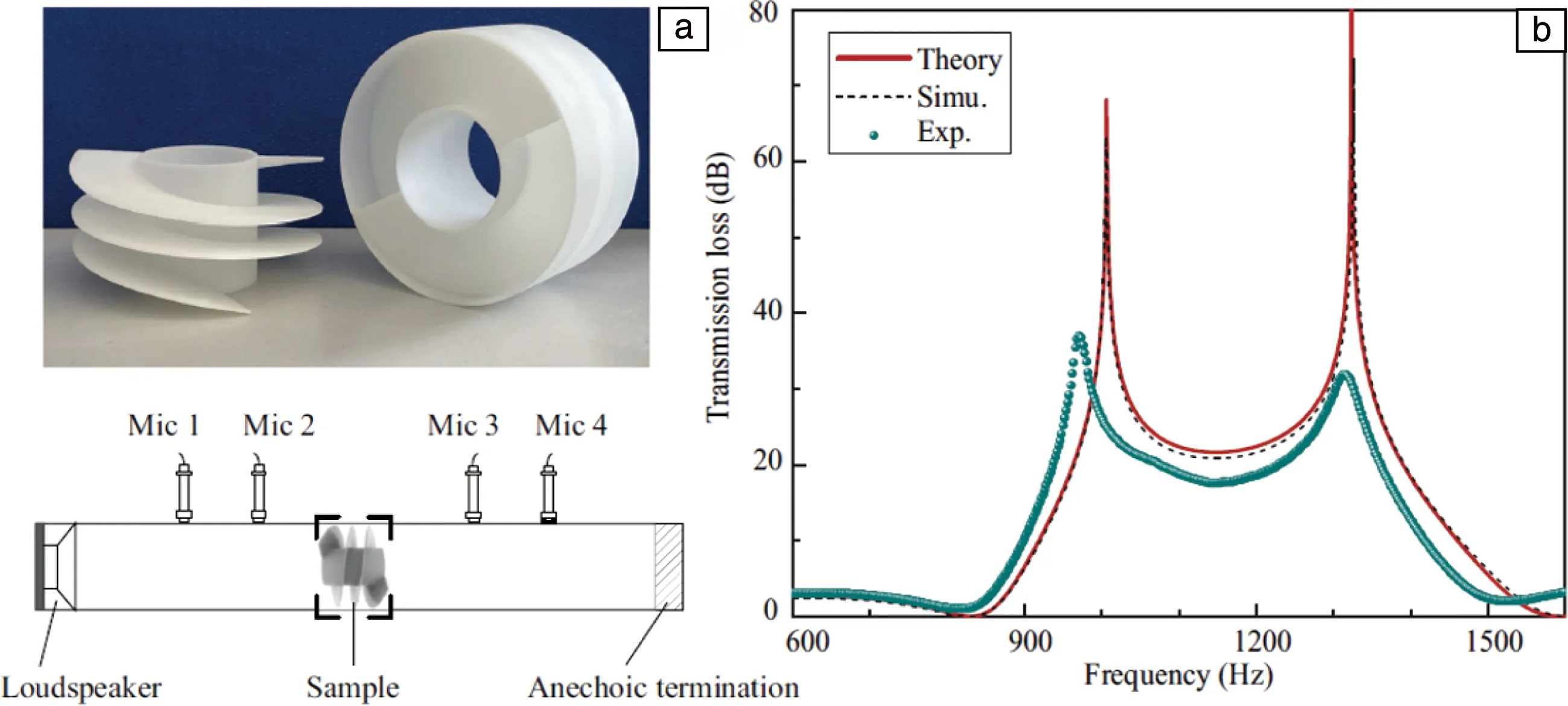
图7 3D打印样品的照片与测试传递损失的装置示意图(a);结构单元的理论、仿真、实验所得传递损失曲线对比(b)[63]Fig.7 Photo of the 3D-printed specimen of the designed unit and schematic of experimental setup for transmission loss measurement(a); Theoretical, simulated and measured transmission loss of the designed unit (b)[63]
2.3 水声超构材料
水声材料是发展海洋装备的基础和重要支撑。传统水声材料存在低频声波调控能力差、体积与重量较大,以及耐压性能差的问题。水声超构材料则为小尺度条件下水下低频噪声振动控制、声隐身、声探测等提供了解决方案[64, 65]。水声超构材料的研究可追溯到20世纪90年代Cherkaev[66]提出的弹性性质与液体相仿的五模材料(pentamode material)。此后,各种水声超构材料在各种空气声、光、电磁超材料的启发下也蓬勃涌现。
目前,水声超构材料按照实现的声功能主要分为吸声[67-69]和水下声隐身。Jiang等[64]通过将梯度的木堆结构引入局域共振型超材料中,使得一个元胞内的两个振子之间的强耦合作用产生新的共振形式,拓宽带隙,可实现水下宽频吸声。随着水下声学隐身斗篷研究的深入,五模材料[70, 71]因其自身的流体属性与固体特征而进入人们的视野。Norris[72]提出了基于五模材料的变换声学理论。Scandrett等[73]解析地研究了三维多层五模材料的声学隐身斗篷的散射,认为可以通过优化每一层的参数来实现较好的声学宽频隐身。水声超构材料的发展尚处于初期,离水下声吸收和声隐身的实际要求还有较大距离,仍存在低频宽带声波调控能力有限、加工制造工艺不足等诸多问题,且未能兼顾结构强度、耐压强度等工作环境要求。然而水声超构材料展现出许多奇特超常的声学特性, 代表了未来水声材料的发展方向。
2.4 声学“黑洞”
声学“黑洞”效应是通过在薄壁结构(通常是梁或板)中嵌入局域不均匀性结构来实现的。这种不均匀性结构的特征是根据空间幂律分布,其几何结构发生变化。Mironov[74]首先提出了这种结构是由壁厚的减小引起局部刚度降低与粘弹性层局部阻尼增强,导致波速的显著降低和衰减特性的显著增强。Krylov[75]指出:因为弹性波在传播时,其速度会平稳连续地下降,因此,在理想情况下,即当壁厚在终点消失时,波速减小为零。这种结构被命名为声学“黑洞”(acoustic black holes,ABH)。ABH典型的几何结构可以分为两大类:用楔形梁制成的典型一维ABH、螺旋形ABH、直径不断增加的分支圆盘的集合(图8a~8c)以及具有轴对称凹坑或槽的二维ABH(图8d~8f)[76]。
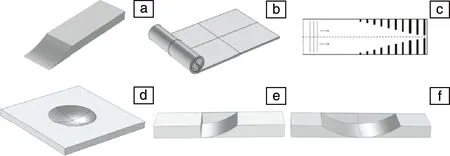
图8 基于幂律分布概念的阻尼结构示例:(a)楔形“黑洞”(acoustic black holes,ABH),(b)螺旋ABH,(c)直径不断增加的分支圆盘的集合;(d)圆形二维ABH,(e)单侧和(f)双侧的ABH槽[76]Fig.8 Examples of retarding structures based on the concept of power-law taper: (a) acoustic black holes (ABH) of tapered wedge, (b) spiral ABH, (c) tubes with axially varying impedance made with a collection of branch discs of increasing diameters; (d) two-dimensional circular ABH, (e) one-sided and (f) two-sided ABH slots[76]
实际制造的楔形件无法达到理想楔形的效果,即使已有一些方法用于改善实际楔形的截断情况(例如通过聚合物薄膜覆盖边缘附近的楔形表面,来形成锐利的边缘),始终具有截断的边缘,楔形厚度的变化对反射系数的影响巨大。Li和Ding[77]对一维ABH的声辐射开展了数值分析和实验研究。由图9数值分析结果可以看出,截断厚度的增加导致43~160 Hz的辐射声功率降低,而626~6000 Hz的辐射声功率增加。其原因是,一方面截断厚度的增加导致的负载质量和等效刚度使得共振频率左移,增强了低频的带宽。另一方面,截断厚度的增加导致ABH中反射系数的增加和波集中度的减小,因此削弱了高频下的噪声抑制。为了达到最佳的降噪性能,需要对截断厚度进行优化。
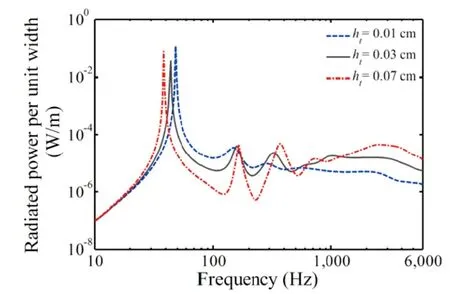
图9 不同截断厚度的声能辐射数值分析结果[77]Fig.9 Effect of the truncation thickness on the radiated sound power based on calculation[77]
对于二维 ABH,需要注意的是,除了几何参数外,ABH的空间布局、主体结构、阻尼材料、中心孔的直径以及ABH的数量也会影响其性能。 Bowyer和Krylov[78]研究了具有各种布局的ABH(图10a)的玻璃纤维复合蜂窝夹心板,并将加速度的实验结果与没有ABH板的基准夹芯板比较,结果表明,从理论上讲,图10b中的结构应该是具有最佳减振性能的布局。

图10 ABH的各种配置(a)和ABH的最佳配置(b)的横截面[78]Fig.10 Cross-section views of sample plates 1~11 (a) and the most effective ABH (b)[78]
研究表明,对于一维ABH而言,几何参数对于ABH效应至关重要。在此之外,其他变量,例如中心孔的直径、ABH阵列的空间布局以及ABH的数量等,也会影响ABH效果[79]。主体结构的材料和阻尼材料对于一维和二维ABH都很重要。几何参数的优化可以显著提高ABH的阻尼效果。ABH的数量及其空间布局可以扩展ABH的有效频率范围。对于主体结构和阻尼层而言,较高的损耗因数可以使用较少的附加阻尼来进一步改善ABH的阻尼效果。3D打印技术使制造更复杂的结构成为可能,被应用在具有ABH功能的结构制备中。需要进一步的研究,将ABH应用于实际中的结构,并对更复杂的结构进行研究。通过以上回顾和总结可以看出,ABH用于振动和噪声控制非常有效,在研究和工业应用中具有巨大的潜力。
2.5 超构声衬
声衬被广泛用于降低管道声辐射,例如空调系统、涡扇发动机等含有气体流动的场景。其中最常见的是穿孔板声衬,该结构可以被视为多个亥姆霍兹共振腔的并联。在切向流存在时,声衬的作用相当于改变流场的边界条件,将“硬边界”转变为由声阻抗描述的“软边界”[55, 80]。
非线性效应和切向流效应主导了声衬的声阻抗,是影响声衬性能的主要因素。非线性效应是由声强引起,一般情况下当声压级超过100 dB时,穿孔板的声阻抗出现明显的非线性效应,小孔处出现涡脱落现象,此时声吸收的原理为声能转化为涡能再耗散为热能。切向流效应是由声衬上方的切向流引起的,由于切向流与声波的相互作用,声衬表面的边界层中的流动存在不稳定性,经典的Ingard-Myers边界条件不再适用[81]。这种不稳定性是由于流体动力模与腔体共振的耦合使共振频率附近的声强被放大,如图11a和11b所示。随着气流马赫数的增大,声衬的声阻线性增加,而声抗略有下降。通过将声衬结构的一个周期单元设计为由两个不同深度的腔体组成,一个小的深度差就能抑制这种不稳定性 (图11c和11d)[82]。
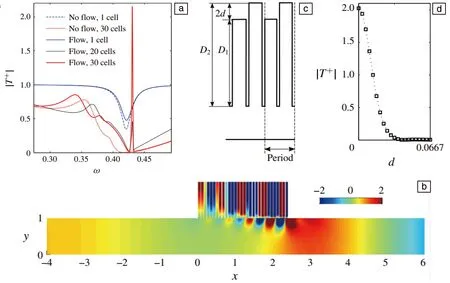
图11 等深共振腔的透射率T+,峰值出现在ω=0.4310(1573 Hz)处(a);声场分布(1573 Hz) (b);不等深共振腔单元示意图(c); T+随深度的变化(1573 Hz)(d)[82]Fig.11 Transmission coefficient T+, the peak occurs at ω=0.4310(1573 Hz) (a); iso-colour plot of the pressure for a plane sound wave (1573 Hz) (b); sketch of periodic cells, each of which consists of two cavities with different depths (c); presenting T+ as a function of depth (1573 Hz)(d)[82]
3 声学超构材料实用化的设计与表征方法
声学超构材料领域相关的基础研究方案已经基本成熟,但是,在面向工程实际情况的实用化研究领域,诸如综合使用传统材料、快速迭代设计等需求对声学超构材料的设计与表征方法提出了新的要求。在本章节,作者基于声学超构材料实用化研究中的一些案例,举例讨论一些实际工作中比较新颖、实用而目前学界较少关注的新的解决方案。
3.1 微观-宏观法
综合使用传统材料,尤其是成本较低的传统多孔材料,可能成为降低声学超构材料生产成本的有效解决方案之一。材料的宏观性能是由其微观结构决定的,即复杂介质中的宏观物理现象,是其内部微观物理现象的总和。在这种思想的指导下,容易得出一个较为简单的、可以理解的物理模型。依据这样的模型,显然划分的单元越细致,对物理现象拟合的精确度越高。而尽可能精确刻画材料的微观结构导致工作量巨大,就目前的计算能力而言,是完全不切实际的。而微观-宏观法(简称“微宏法”)的出现旨在通过有限元、边界元[83]等数值计算工具和越来越强大的计算机计算能力,解决以上两个问题[84]。Huang等[53]基于对疏松排列的秸秆束具有宽带吸声性能现象的观察,研究了基于天然材料或仿生结构的宽带吸声超构材料,将既有的声学多孔材料Biot理论的传统半经验模型与局域共振、多重散射等超构材料理论模型相结合,利用多阶渐进的微观-宏观法均质化模型统一了多孔材料声场与超构材料局域共振声场,探索了基于多孔材料理论的声学超构材料。
3.2 借助机器学习的结构优化
基于声学超构材料,为了实现精密的声学功能,需要更加复杂的结构组合,而结构愈加复杂,设计就更具挑战性。单纯依靠人工设计、甚至单一使用传统的优化设计方案,已经不能完全满足日趋复杂的声学超构材料功能基元设计。为了进一步降低研发成本,要更多地借助计算机辅助设计,在复杂的结构设计中寻找更加易于实现的设计。
传统的设计策略是基于优化算法,典型过程是先开始生成一个随机的结构,然后仿真模拟,将模拟结果与设定的目标相比较,然后改变结构计算、更新其设计,迭代这个过程得到符合要求的设计。常用进化算法[85]、水平集算法[86]、伴随算法[87]等来优化某个特定几何参数。由于每一个仿真计算资源消耗都较大,而通常需要计算数百乃至数千次才能得到可用的优化结果,基于此类方法的优化都极为缓慢。
近年来,数据驱动的机器学习[88-91]在学术界和工业界方兴未艾。与传统优化算法不同,机器学习可以通过训练人工神经网络来助力设计优化进程[92],我们可以构造一个前馈神经网络,输入层采用结构几何参数,输出层为仿真结果的表征,如传递损失,通过反向传播算法得到训练好的神经网络。用神经网络来替代具体的仿真程序,可以极大缩减计算时间,之后可以将仿真结果作为输入层,结构参数作为输出层,这种神经网络称之为逆向设计。通过训练好的神经网络来获取所需要的优化结果仅需几秒钟,因为这个过程不需要任何的迭代计算。
3.3 吸声系数测量方法
声学超构材料主要用途之一是用于实现吸声降噪。通常用于测试表征声学材料的吸声系数(阻抗)的方法主要是阻抗管法和混响室法。阻抗管法测试基于两个麦克风之间的传递函数,求解吸声系数与频率之间的函数关系[25, 26]。这种方法要求材料必须平整,大小也要符合阻抗管截面形状,从而对设计声学超构材料的结构形状有了一定的约束,同时测试频率也有相应的上下限,优点是测量较为准确。
混响室法是一种统计声学的测试方法[29],其结果没有精确解,不同实验室测试吸声系数会有差别,且在低频段测量误差会高于高频段,因为低频场混响条件更难满足,但测试时对样品形状结构并无限制,较为方便。标准混响室体积需大于200 m3,试件面积至少为10 m2,而一般超构材料所涉及的面积远远小于该尺寸。为了解决这一问题,出现了基于合成扩散声场原理的小型混响舱测试法[93]。这一方法参考混响室法的标准,混响舱体积可以缩减到6~9 m3,所需材料样品的面积也相应缩减到1~2 m2,可用于测量材料在400 Hz频段以上的随机入射场吸声系数。
与前两种方法不同,近年来兴起了基于声矢量传感器的近场阻抗测量法[30]。这种探头可以像普通麦克风测量声压一样方便地测量声质点振速。由于是近场测试,因而对材料结构形状没有限制,对频率范围、声场也没有约束,同时环境噪声及声反射对这种近场测试影响也比较小。这是一种先进的、有广阔应用前景的方法。
4 结 语
本文通过对吸声、隔声、水声超构材料以及声学黑洞等不同功能和原理的声学超构材料及相关研究实例的简要介绍,讨论了各类声学超构材料的巨大应用潜力和相关实用化研究所面临的机遇和挑战。
在此基础之上,结合我国新时期建设发展的实际需求,在此探讨、展望未来5~10年声学超构材料实用化研究的方向。在功能层面,声学超构材料能够复合更多的实用功能。例如,复合疏水疏油的表面材料,使其具备良好的抗污功能;结合光催化材料复合甲醛降解功能;附加骨架和超结构,使其具备良好力学性能,可以独立构成轻质隔墙等。在应用层面,可以利用声学超构材料不完全依赖材料本体特性的属性,发展适用于低频(100~800 Hz)、超低频(0~100 Hz)、高流速(0.5~1 Ma)、高低温(200 ℃以上、0 ℃以下)、高低压(大于0.1~0.3 MPa、小于0.03 MPa)等极端工况和面向极端使役条件的声学材料。依托声学超构材料,发展多功能声学材料,应当是声学超构材料实用化发展的一大特色。
在设计层面,依托最新发展的超级计算、云计算等高速计算技术,已经能够对声学超构材料功能基元及其序构进行比较精细化的模拟仿真。通过足够的经验数据的积累,在此基础上通过机器学习和人工智能的算法,突破传统设计方法的限制来设计声学超构材料,真正实现声学材料从微结构到生产制备工艺的全链路正向设计,最终实现依据目标性能的逆向设计。
总体来看,从声学超构材料问世之初,因其特有的新奇功能性就被寄予厚望。而近20年来的发展,使得声学超构材料的基础研究已经积累了丰富的成果。这些成果充分展示了其巨大的应用潜力。面向未来,在继续对拓扑声学、PT对称性等前沿进行攻关,发现新功能、突破极限性能的基础上,声学超构材料必须向工程化、实用化转变,解决和突破现有材料在声学工程中碰到的难题和瓶颈问题,以期在工业、国防和民生领域发挥重要作用。
