考虑应变依赖性特征的硬涂层整体叶盘非线性减振分析
2021-03-17高峰刘秀婷
高峰,刘秀婷
(1.南京信息工程大学滨江学院自动化学院,江苏无锡,214105;2.东北大学航空动力装备振动及控制教育部重点实验室,辽宁沈阳,110819;3.东北大学材料各向异性与织构教育部重点实验室,辽宁沈阳,110819)
随着航空发动机在大推力与轻量化方向的快速发展,无榫结构(通过整体加工或焊接制造)的整体叶盘得到越来越广泛的应用[1]。由于缺少榫头和榫槽的摩擦耗能,整体叶盘的系统阻尼通常较小,振动应力或响应过大,振动的不利影响比较突出。在恶劣工况下,整体叶盘容易发生共振和高周疲劳破坏,从而缩短其有效使用寿命[2]。基于此,有必要对整体叶盘附加外部阻尼器来实现结构件的阻尼减振。对于传统的榫接叶盘结构,大多数研究人员通常应用干摩擦阻尼器(叶冠[3−4]、凸肩[5−6]或缘板[7−8]等)和黏弹性材料[9−10]来消耗振动能量,达到有效减振。但是,整体叶盘的结构特征和工作环境决定了上述传统的阻尼减振措施是无法实施的。因此,迫切需要一种新型的阻尼器来抑制整体叶盘过大的振动响应。
硬涂层主要是由金属基(NiCoCrAlY等)、陶瓷基(YSZ 等)或两者混合组成的涂层材料[11−12]。与软涂层不同,硬涂层通常具有抗高温、抗摩擦、抗冲刷和抗腐蚀[13−17]等诸多优点,一般用于结构件的表面强化处理。研究发现,硬涂层材料内部颗粒的摩擦使其具有良好的系统阻尼[18−19],可以在较大温变范围内实施被动阻尼减振[20−22],而且可灵活调整附加刚度。此外,硬涂层的力学参数具有典型的非线性特征,其储能模量(弹性模量)与耗能模量(损耗因子)总是随着涂层结构件应变的变化而变化,称为应变依赖性[23−25]。目前,研究人员以板、梁和薄壁圆柱壳[25−27]为对象,对涂层复合结构的非线性振动特性展开了基础研究,但是,在考虑应变依赖性的前提下对涂层整体叶盘非线性振动特性的研究较少。
Rayleigh-Ritz法是通过泛函驻值条件求未知函数的一种近似方法,也是应用于应用数学和机械工程领域的经典数值方法,可以高效率地计算结构的低阶自然频率,被广泛用于求解边界和连续性条件复杂的结构振动问题。针对复杂形状板结构,张俊等[28]对传统的Rayleigh-Ritz 法进行改进,并求解了直边和曲边板的振动特性,与有限元结果的对比证明了改进方法具有的较高的准确性和可靠性以及良好的适应性。在建立具有形状记忆合金(SMA)纤维的各向异性层合梁本构方程的基础上,徐晓明等[29]利用Rayleigh-Ritz能量法求板簧的固有频率,并得到固有频率与温度、铺层角和SMA含量的关系曲线,揭示了SMA纤维复合材料变截面板簧的固有频率的调节机理。
本文作者利用硬涂层的阻尼特性来增强整体叶盘的耗能减振,并在考虑硬涂层应变依赖性的前提下求解涂层整体叶盘非线性振动特性。选择叶片两侧附加等厚度的非线性NiCoCrAlY+YSZ硬涂层的整体叶盘为研究实例,首先,根据实验离散数据并利用高阶多项式阐述硬涂层非线性力学参数的连续变化趋势,然后,利用改进的Oberst梁理论、基于正交多项式的Rayleigh-Ritz能量法建立涂层整体叶盘的非线性振动模型,最后,利用提出的基于Newton-Raphson 法迭代求解程序求解涂层整体叶盘的非线性振动模型,得到非线性共振频率和共振响应,并通过与实验测试数据的比较校验模型;通过线性与非线性振动特性的比较分析了应变依赖性弹性模量和损耗因子对涂层整体叶盘共振频率和共振响应的影响。
1 硬涂层的应变依赖性
通过研究发现,硬涂层材料的阻尼特性具有以下特点:1)硬涂层的阻尼性能要优于金属基体的阻尼性能,但是比黏弹性材料的性能差;2)在高温高压环境下,硬涂层的阻尼性能能够保持稳定,而不会像黏弹性材料那样失效;3)硬涂层的模量随着涂层复合结构应变的变化而变化。
硬涂层的应变依赖性复模量为
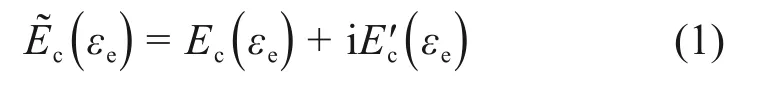
式中:εe,Ec(εe)和E′c(εe)分别为硬涂层的等效应变、弹性模量和耗能模量;i表示虚数。
根据文献[30]可将Ec(εe)和E′c(εe)进行多项式展开,分别表示为
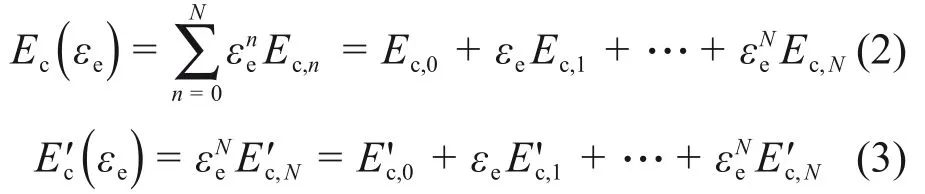
式中:n和N分别为多项式项数和最大项;Ec,0和E′c,0分别为硬涂层的线性弹性模量和耗能模量。
将式(2)~(3)代入式(1)并整理可得硬涂层的复模量和损耗因子ηc(εe)分别为

2 涂层整体叶盘的非线性振动特性分析
2.1 非线性振动建模
图1所示为叶片两侧附加非线性硬涂层的整体叶盘。整体叶盘的密度为ρ,涂层叶片的长度、宽度、厚度和密度分别为l,b,hcb(其中,叶片厚度为hb,涂层厚度为hc)和ρcb,矩形横截面积为Ap,安装角和圆周角分别为ϕp和θp(p表示叶片数量);轮盘外径、内径和厚度分别为Ro,Ri和hd。由于轮盘刚度与叶片的刚度相近,因此,在两者之间引入弹簧(平动刚度KTp和转动刚度KRp)来考虑其耦合振动特性。在数算例中,以涂层叶片中心Op为原点建立局部直角坐标系(xp,zp),以轮盘中心Od为原点建立圆柱坐标系(r,θ,z)。此外,涂层整体叶盘以恒定角速度Ω绕z轴旋转。为了计算简洁,引入以下量纲一的量:

仅考虑轮盘在z轴方向的位移wd和涂层叶片在zp方向上的位移wbp,分别为:
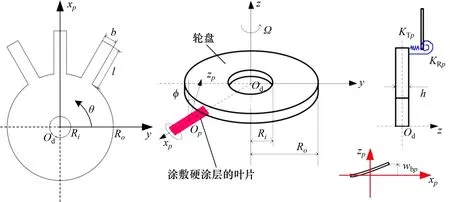
图1 涂层整体叶盘的非线性动力学模型Fig.1 Nonlinear dynamic model of blisk deposited hard coating on blades
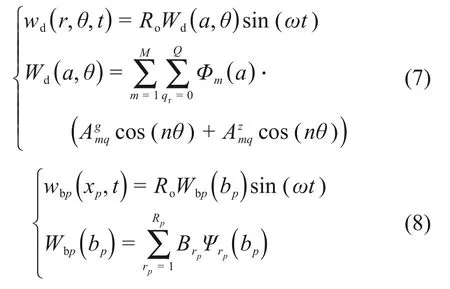
式中,,和Brp为待求解系数,qr为轮盘节径数;M和Rp为Ritz 基底维数,Φm(a)和Ψrp(bp)为Ritz 基的容许函数,是通过Gram-Schmidt 方法得到的正交多项式。
2.2 非线性振动模型的建立
2.2.1 涂层叶片等效参数求解
图2所示为涂层叶片和复合Oberst 梁的示意图。在复合材料结构的数值计算中,通常可以将多层不同种类材料组成的复杂结构等效成一种同质的特殊材料,从而能够在不影响计算精度的情况下有效提高分析效率[31],因此,首先基于改进的Oberst梁理论获得涂层叶片的等效参数。
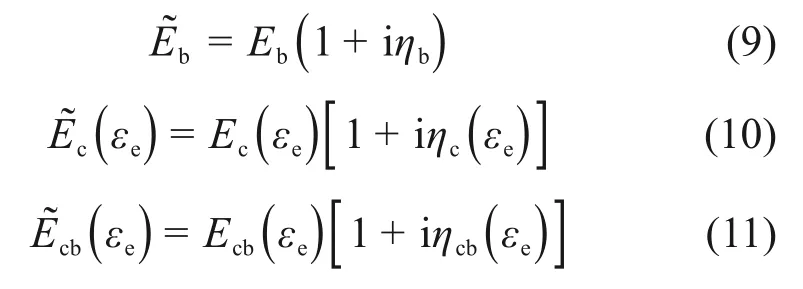
式中:Eb和ηb分别为叶片的弹性模量和损耗因子;Ecb(εe)和ηcb(εe)分别为涂层叶片的非线性弹性模量和非线性损耗因子。
涂层叶片在弯曲状态的平衡方程为
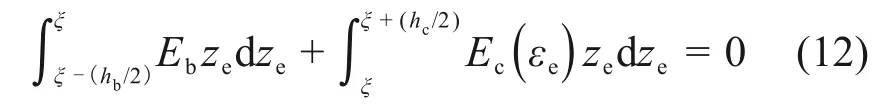
则涂层叶片结合面到中性面的距离ξ为
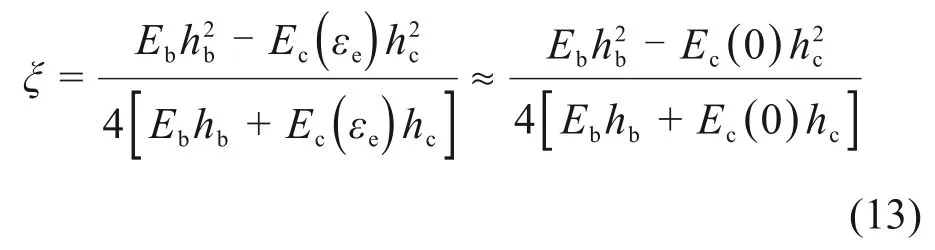
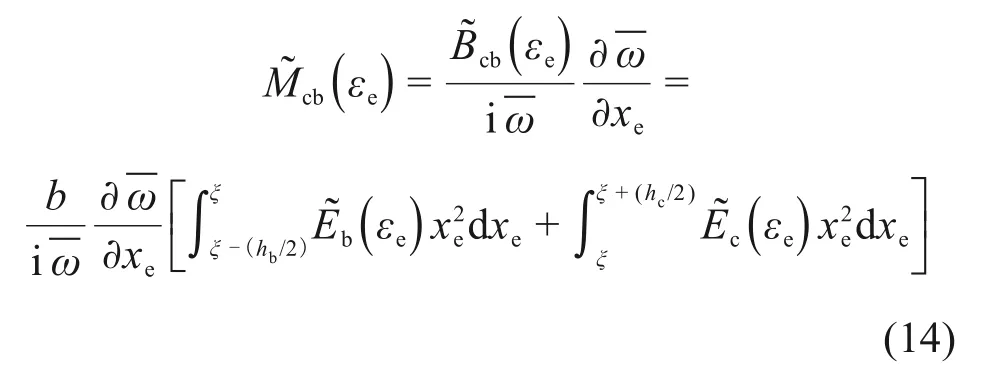
则涂层叶片的复弯曲刚度为
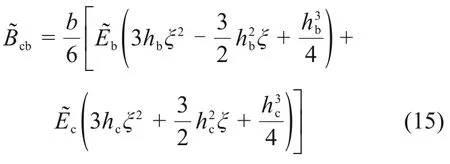
将式(13)代入式(15)可得
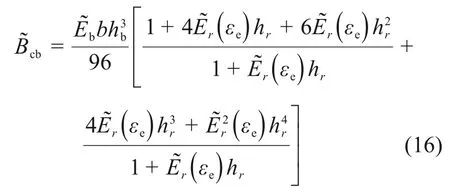
式中:hr=hc/hb,Er(εe)=Ec(εe)/Eb。
此外,涂层叶片的复弯曲刚度满足关系:
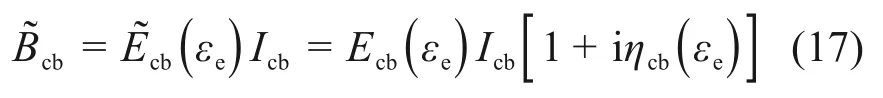
将式(16)和式(17)联立,并整理可得

图2 涂层叶片和涂层梁的示意图Fig.2 Schematic diagrams of the coated blade and composite beam
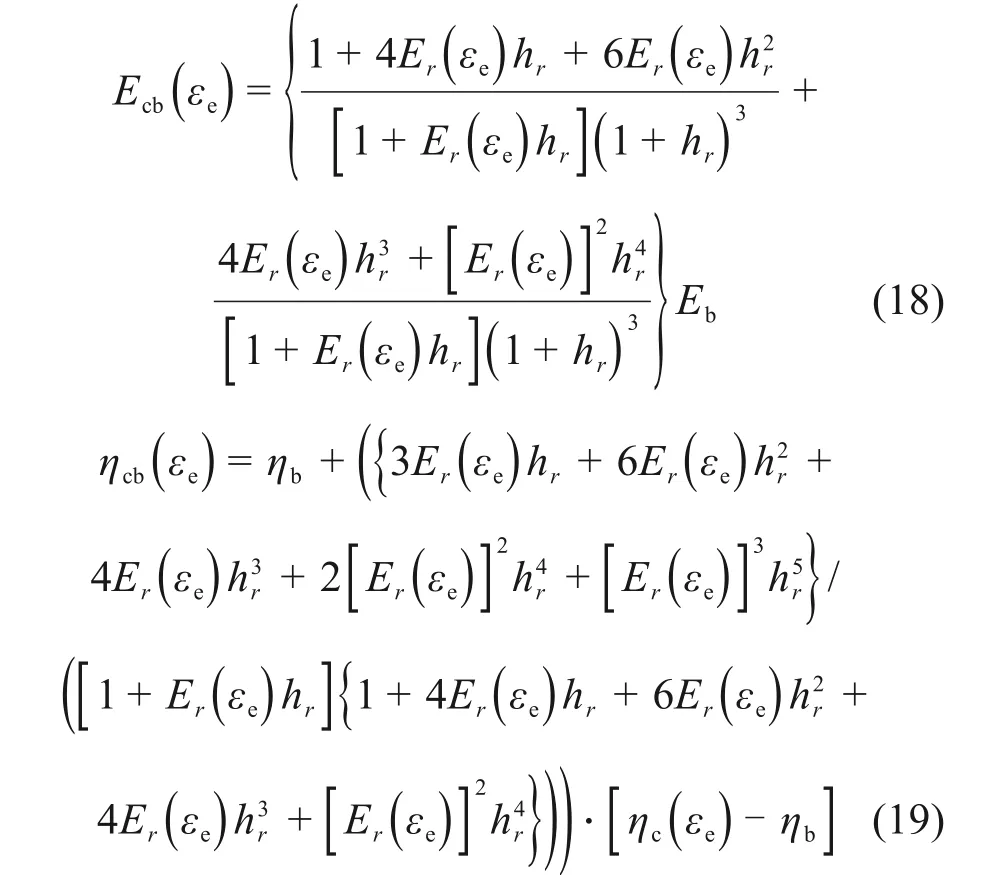
2.2.2 非线性振动方程的推导
由图1可知,旋转态的涂层整体叶盘包含涂层叶片和轮盘转动动能、势能、应变能以及弹簧的应变能,因此可以利用基于能量的Rayleigh-Ritz法来推导涂层整体叶盘非线性振动方程。
涂层叶片和轮盘的动能Tcb和Td分别为
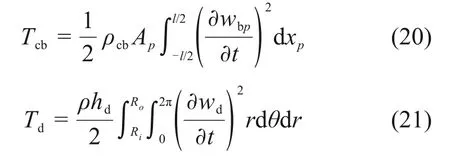
涂层叶片和轮盘的应变能Ucb和Ud分别为
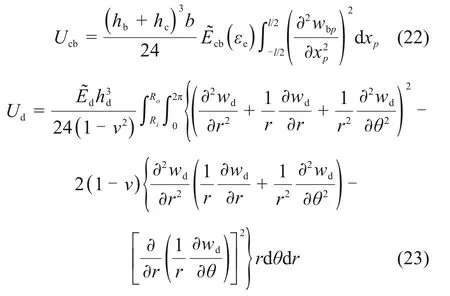
弹簧和涂层叶片的势能Vs和Vcb的分别为
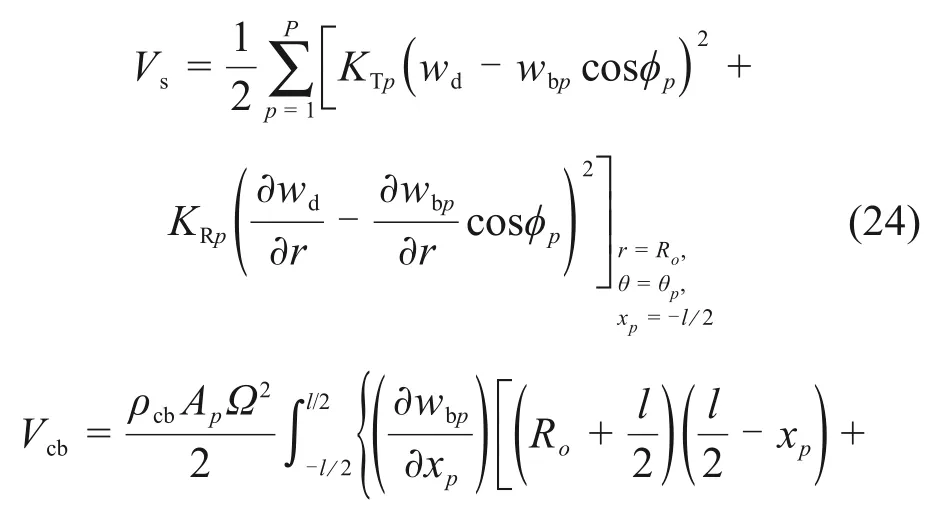
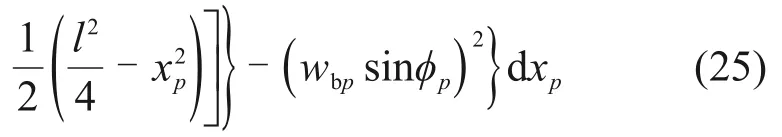
轮盘的势能Vd为[33]
式中:σr和σθ分别为轮盘径向力和圆周力[34];u为轮盘的面内位移;Mcb和Md分别为涂层叶片和轮盘的质量。
将能量式(20)~(28)代入Lagrange公式,得
根据最小势能原理求解式(29)或L的极小值,可得到涂层整体叶盘的非线性频率方程为

式中:(εe)和M分别为涂层整体叶盘的非线性复刚度矩阵和线性实质量矩阵;Kcb(εe)和Dcb(εe)分别为涂层整体叶盘的非线性刚度矩阵和非线性阻尼矩阵;和φ分别为涂层整体叶盘的复特征值和特征向量。
由式(30)可以得到涂层整体叶盘的非线性振动方程为

式中:ωcb和q分别为涂层整体叶盘的固有频率和受迫振动响应;F为涂层整体叶盘的力向量。
为了充分考虑应变依赖性对涂层整体叶盘振动特性的影响,需要准确计算式(31)的等效应变εe。根据文献[26]可知,等效应变εe可以通过如下公式求解:
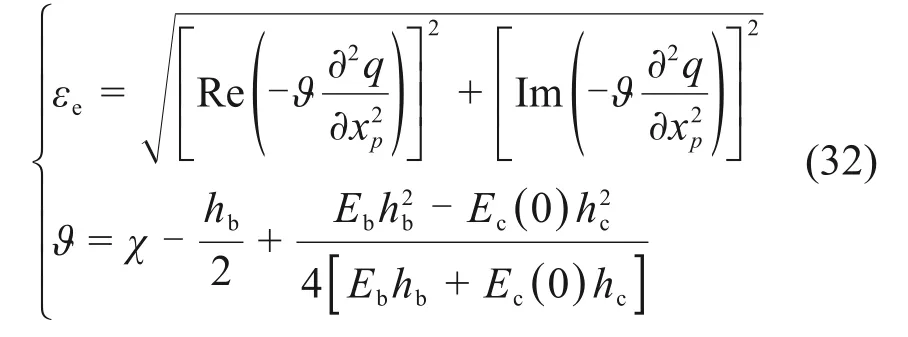
式中,χ为拾振点到涂层叶片中性面的距离。
2.3 非线性振动特性的求解
令等效应变εe=0,依据上述方法可得到不考虑应变依赖性的涂层整体叶盘的复刚度矩阵,即

整体叶盘的振动特性在叶片附加硬涂层后会发生改变,这种变化与整体叶盘发生失谐的变化非常相似,因此,将硬涂层假设成一种具有谐调形式的失谐特征,即由硬涂层构造特殊失谐特征的整体叶盘的扇区物理和几何参数完全相同。此外,由于硬涂层厚度较整体叶盘相对较小,因此,假设涂层叶片厚度近似为叶片的厚度。换句话说,认为对叶片涂敷硬涂层仅仅改变整体叶盘材料参数而不改变其几何参数。基于上述假设,由式(30)和式(33)可得到硬涂层的非线性复刚度矩阵:
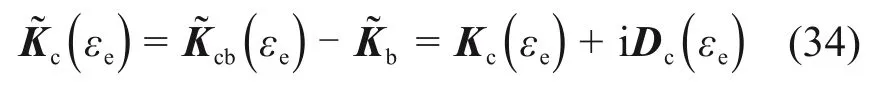
此外,由式(31)可以得到涂层整体叶盘非线性振动方程的残余向量ζ为
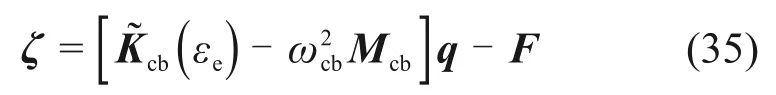
将式(2),(3)和(34)代入式(35),经整理可得
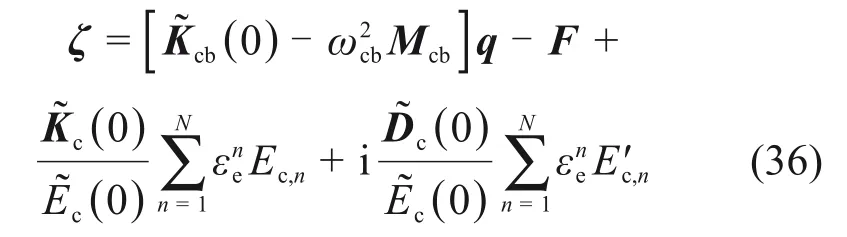
需要注意的是,复模量理论的应用使得涂层整体叶盘的受迫振动响应q是以复数形式存在,表示为

为了求解涂层整体叶盘的非线性振动工程,提出一种基于Newton-Raphson法的迭代计算方法。其中,第r+ 1次的迭代公式为
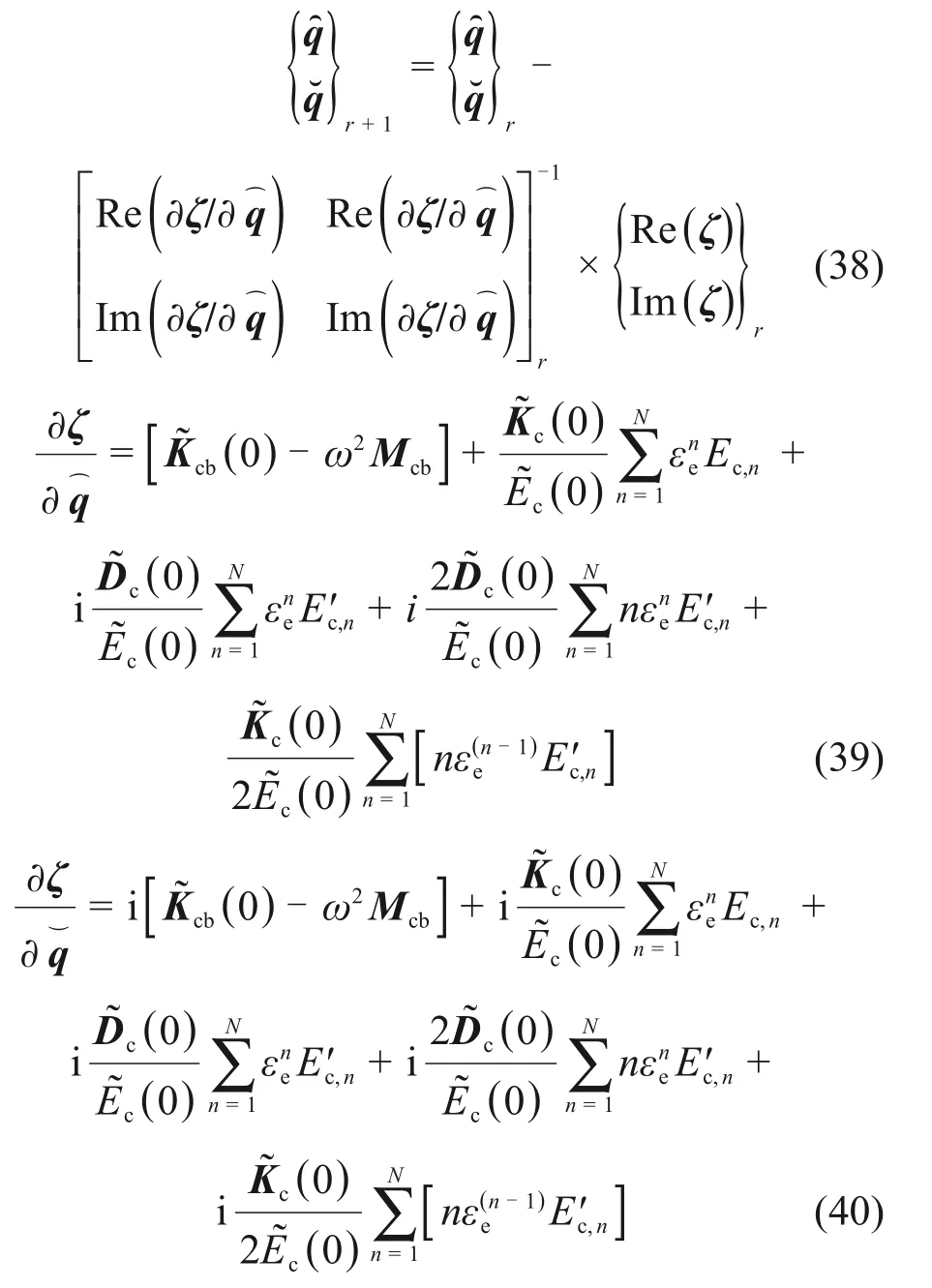
假设迭代计算精度为ℓ,则可设定残余向量的二阶范数作为迭代计算的终止条件:
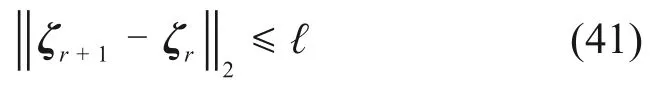
值得注意的是,硬涂层的等效应变εe在非线性振动方程迭代计算的初始值为0,涂层整体叶盘的非线性复模量和受迫振动响应q会基于前一次的计算结果不断更新,直至满足预设的计算精度为止。
3 实例分析
图3所示为涂层整体叶盘的试验件和实验系统。整体叶盘厚度为3 mm,硬涂层厚度为0.3 mm。轮盘的内、外径分别为80 mm 和100 mm,叶片的宽度和长度分别为24 mm 和80 mm。弹簧的平动和转动刚度均为10 MN/m。涂层整体叶盘的材料参数见表1。其中,考虑应变依赖性的硬涂层的非线性弹性模量Ec(εe)与损耗因子ηc(εe)分别为[35]
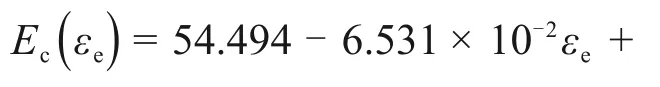
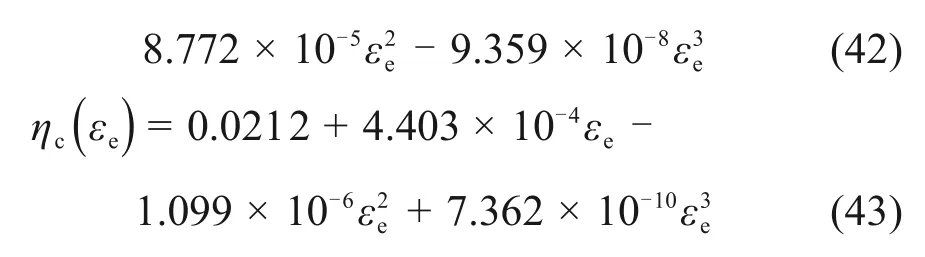

图3 涂层整体叶盘及其实验设备与测试流程Fig.3 Experimental devices and testing process of coating blisk

表1 整体叶盘和硬涂层的材料参数Table 1 Material parameters of academic blisk and hard coating
在振动实验中,首先,对涂层整体叶盘进行模态测试确定大致的固有频率,再对涂层整体叶盘进行扫频测试确定准确的共振频率与响应。需要注意的是,由于NiCoCrAlY+YSZ硬涂层会使整体叶盘的频率降低[2],因此,在进行扫频实验时,需要由高阶向低阶测试。
3.1 非线性振动模型的校验
为了校验非线性涂层整体叶盘的非线性振动模型的有效性和可靠性,将理论结果和实验结果进行对比。表2所示为基于非线性振动模型和实验测试得到涂层整体叶盘在相同激励下的共振频率和响应。从表2可以发现:涂层整体叶盘共振频率或共振响应的理论结果与实验结果都存在一定的相对误差,但是它们的相对误差不是很大,共振频率的相对误差始终保持在1.04%~1.98%的范围内;共振响应的相对误差大多在20%以内,而且最大值不超过28.21%。这说明在相同的激励水平下,本文创建的涂层整体叶盘的非线性振动模型具有较高的计算精度和较好的可靠性。
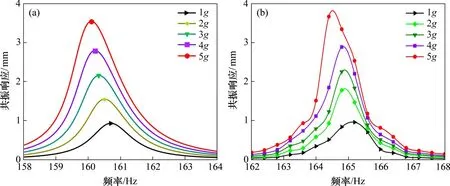
图4所示为基于非线性振动模型和实验测试得到涂层整体叶盘在不同激励下(在第二阶次)的频域响应曲线。从图4可以看出:涂层整体叶盘在不同激励下的理论响应和实验响应存在一定偏差,但是这些差异并不大,而且理论分析结果与实验测试结果具有非常相似的变化趋势,即随着激励的增大,涂层整体叶盘的理论和实验共振响应均逐渐增大,响应峰值所对应的共振频率均逐渐减小。这说明在不同外部激励水平下,涂层整体叶盘振动特性的理论分析结果与实验测试结果具有较好的一致性。
3.2 应变依赖性对振动特性的影响
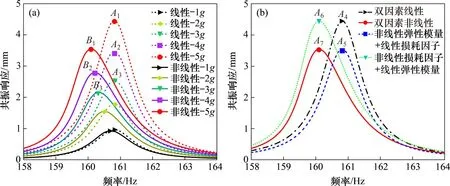
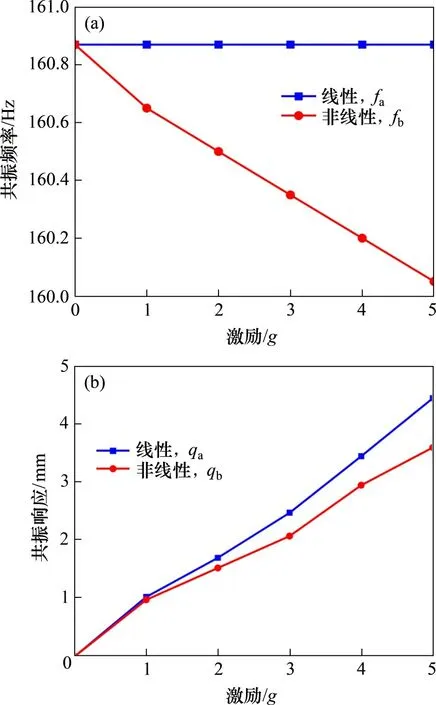
图5所示为涂层整体叶盘的线性和非线性(第二阶次)频率响应线。图中,A1~A7和B1~B3表示共振响应曲线峰值位置。双因素非线性是指弹性模量和损耗因子均为非线性的情况;单因素非线性是指弹性模量和损耗因子中仅一项为线性,另一项为非线性的情况。从图5(a)可见,在相同的激励水平下,应变依赖性会使得涂层整体叶盘的共振频率f略微减小(即fB1 表2 涂层整体叶盘在1g激励下的共振频率和响应Table 2 Resonant frequencies andresponses of coating blisk under 1g excitation level 图4 涂层整体叶盘在不同激励下的频率响应曲线Fig.4 Frequency−response curves of coating blisk under various excitation levels 图5 涂层整体叶盘的线性和非线性频率响应曲线Fig.5 Linear and nonlinear frequency−response curves of coating blisk 图6所示为涂层整体叶盘在不同激励下的线性和非线性(在第二阶次)共振频率与共振响应,其中,qa和qb分别为不考虑应变依赖性和考虑应变依赖性的涂层整体叶盘的共振响应,fa和fb分别为不考虑应变依赖性和考虑应变依赖性的涂层整体叶盘的共振频率。由图6(a)可以看到:随着外部激励的增大,不考虑应变依赖性的涂层整体叶盘的共振频率fa保持恒定不变,考虑应变依赖性的涂层整体叶盘的共振频率fb呈下降趋势。由图6(b)可以看到:随着外部激励的增大,考虑或不考虑应变依赖性的涂层整体叶盘的共振响应qa或qb都会逐渐变大,但是,考虑应变依赖性的共振响应增加量∆qb要明显小于考虑应变依赖性的共振响应增加量∆qa,且共振响应增加量的差值(∆qa−∆qb)也逐渐增大,这说明应变依赖性能够增强硬涂层对整体叶盘的振动控制能力。 图6 涂层整体叶盘的线性和非线性共振频率与响应Fig.6 Linear and nonlinear resonant frequencies and responses of coating blisk 1)利用改进的Oberst 梁理论、基于正交多项式Rayleigh-Ritz 能量法和Newton-Raphson 法建立的考虑应变依赖性的涂层整体叶盘的非线性振动模型具有较高的计算精度和较好的可靠性。 2)应变依赖性弹性模量仅对涂层整体叶盘的共振频率产生影响,应变依赖性损耗因子仅对涂层整体叶盘的共振响应产生影响。 3)应变依赖性对涂层整体叶盘共振频率的影响较弱,但能明显提升硬涂层的振动阻尼能力,有助于硬涂层提高整体叶盘的阻尼减振效果。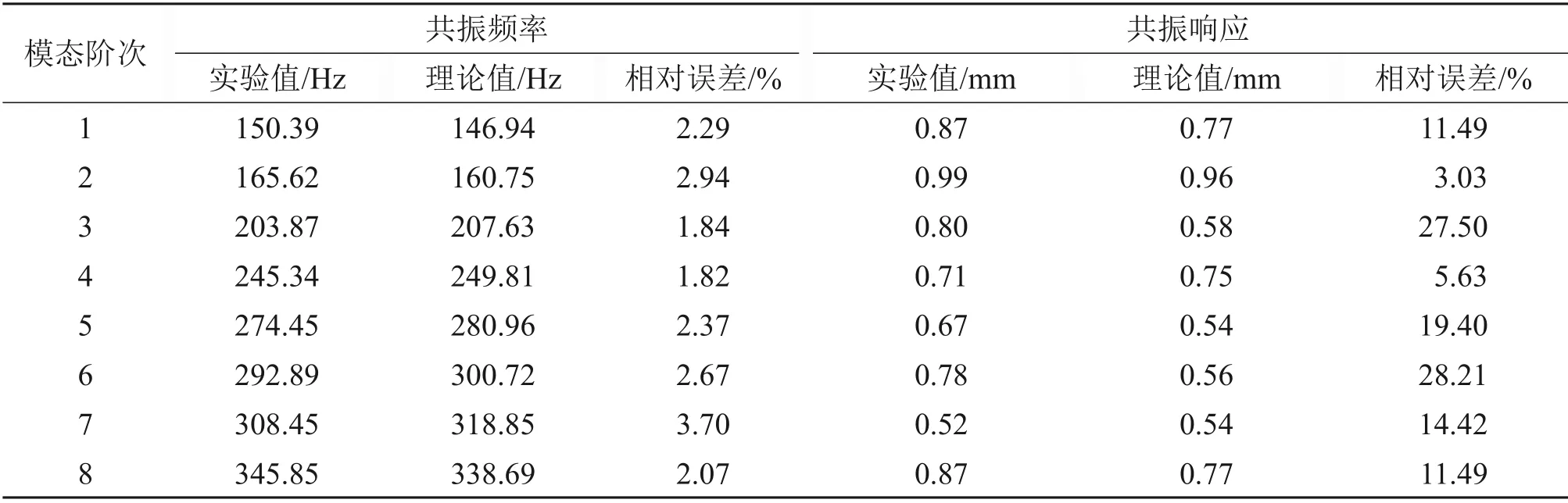
4 结论
