铁道车辆车轮跳轨全过程计算方法

2021-03-17向俊陈林苏玮杨海明龚凯彭子祥

中南大学学报（自然科学版） 2021年2期

向俊，陈林，苏玮，杨海明，龚凯，彭子祥

(1.中南大学土木工程学院，湖南长沙，410075；2.华东交通大学土木建筑学院，江西南昌，330013)

列车脱轨问题一直是铁路工作者的研究重点与难点，此问题很复杂，导致列车脱轨问题一直未能得到有效解决。曾庆元等[1]突破传统的研究方法，提出了列车脱轨能量随机分析方法，并在最近10 几年来，于高速与重载铁路上得到应用。龚凯等[2−4]应用此方法，研究了诸多因素对货物列车运行安全性的影响规律，并提出了一些良好的工程措施。YU等[5−6]应用此方法，研究了无砟轨道诸多病害对高速列车运行安全性的影响规律，并提出了相应措施及无砟轨道维修标准建议方案。尽管如此，此方法也只是针对爬轨脱轨进行了研究，并未对跳轨脱轨进行研究。试验结果表明，随着列车速度不断提高，列车车轮更易发生跳轨(即车轮与钢轨分离)现象，严重时将导致列车脱轨事故发生，这对列车运行安全性直接构成威胁，因此，需进一步研究考虑跳轨脱轨的列车脱轨能量随机分析方法。FRÝBA 等[7]研究了车轮跳轨现象及二轴车辆跳离钢轨的车桥振动问题，指出了考虑跳轨现象的必要性。LEE[8−9]采用车轮与钢轨刚性接触模型，研究了单个车轮跳离钢轨的车桥振动问题。LIU 等[10−11]研究了车辆在桥梁上的跳轨问题。STÂNCIOIU 等[12−13]研究了单轴及两轴车辆模型在简支梁上的跳轨问题。CHENG 等[14]采用车轮与钢轨刚性接触模型，研究了单个轮对跳离钢轨的车桥振动问题。BAEZA 等[15]研究了单轴车辆在简支桁梁上的跳轨问题。翟婉明[16]建立了单轮对−轨道相互作用模型，对单轮对爬轨和跳轨两种工况下的脱轨行为进行了计算分析。娄平[17]基于轮轨刚性接触模型，研究了二轴车辆跳离桥梁结构的振动问题，模拟了车轮与钢轨接触、跳离、再次接触的动态过程。曾京等[18−19]分析了轮对横向冲击对车轮跳轨的影响规律。肖新标等[20−21]研究了复杂环境状态下的轮轨分离现象，建立了判断轮轨是否分离的指标。孙丽霞等[22]研究了车辆蛇形运动对于跳轨脱轨的影响。XU 等[23]在空间车轨模型中建立了时变耦合矩阵，简化了轮轨分离时的振动方程的形式。ZHANG 等[24]通过考虑分离和路面不平顺的车桥相互作用的非线性多弹簧模型发现，无论是否从桥上分离，其耦合的控制方程式都不会改变。JU[25]建立了一种非线性轮轨接触单元模型，可以模拟轮轨密贴、滑动和分离。由此可见，国内外对铁道车辆车轮跳轨全过程计算方面的研究太少，并未取得令人满意的结果。文献[7−12,24]没有考虑轨道振动及轮轨冲击作用。文献[13−15]虽然考虑了轮轨冲击作用，但是没有考虑轨道振动。文献[16,17,23]虽然考虑了轨道振动，但在轮轨再次密贴时，没有考虑轮轨冲击作用。文献[18−22]主要考虑了轮轨横向振动与冲击对跳轨脱轨的影响。

本文提出一种铁道车辆车轮跳轨全过程的计算方法，同时考虑轨道振动与轮轨冲击作用，可以反映车轮跳轨全过程的完整信息，以便为进一步研究考虑跳轨脱轨的列车脱轨能量随机分析方法打下良好基础。

1 车轮跳轨的基本特征

跳轨车轮的位移及轮轨力可以直接表征车轮跳轨的基本特征，如图1所示。

跳轨车轮的位移基本特征表现为车轮经历了从轮轨密贴—车轮上升、车轮下降—轮轨密贴的全过程。图1(a)所示为跳轨车轮的跳轨高度h时程曲线。从图1(a)可见：在列车正常行驶过程中，所有车轮与钢轨之间保持密贴关系；当列车中的某车轮在跳轨诱因作用下发生轮轨分离时，车轮就会从t1开始起跳而上升，直到tz上升到最高点，车轮跳轨高度h达到最大值hmax，之后开始下降，直到t2落在钢轨上，又维持了轮轨密贴状态(这里假定车轮没有发生跳轨脱轨)。

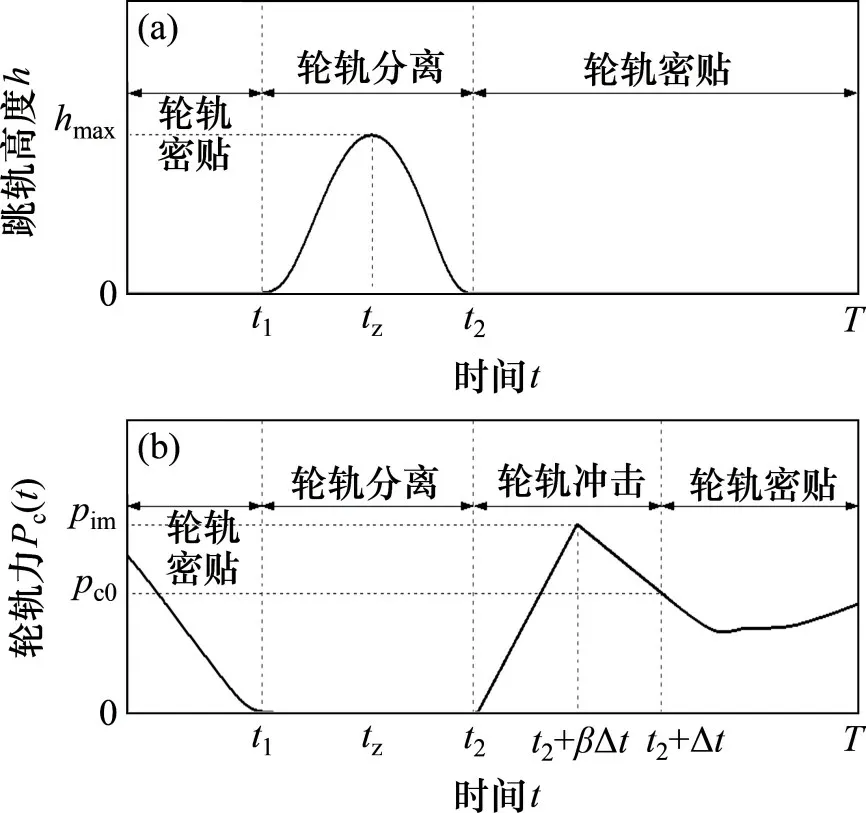
图1 时程曲线示意图Fig.1 Schematic diagram of time histories

跳轨车轮的轮轨力基本特征表现为4 个阶段，即轮轨密贴、轮轨分离、轮轨冲击及轮轨再次密贴。图1(b)所示为跳轨车轮的轮轨力Pc(t)时程曲线。从图1(b)可见：在列车正常行驶过程中，车轮与钢轨间的相互作用力处于轮轨密贴状态下的幅值水平；当列车中的某车轮在跳轨诱因作用下发生轮轨分离时，从t1至t2，轮轨力保持为0；在t2时，轮轨本应保持紧贴状态，但由于跳轨车轮与钢轨之间存在相对速度，从而产生轮轨冲击力，并在t2+βΔt时达到最大值(其中，β为小于1 的正数，并在计算时根据精度要求加以确定)。在经历了冲击时间Δt后，又恢复到轮轨密贴状态下的幅值水平。

由图1(a)可见：从t2至计算终点时刻T，轮轨保持密贴状态。由图1(b)可见：从t2至t2+ Δt，虽然轮轨处于密贴状态，但轮轨之间产生了冲击力，之后才恢复到正常密贴状态下的幅值水平。根据跳轨车轮的轮轨力基本特征，可将车轮跳轨全过程划分为轮轨密贴(第Ⅰ阶段)、轮轨分离(第Ⅱ阶段)、轮轨冲击(第Ⅲ阶段)及轮轨再次密贴(第Ⅳ阶段)共4个阶段。

由此可见，除了第Ⅰ与Ⅳ阶段具有共同动力学特征外，其他各阶段具有完全不同的动力学特征，尤其体现在它们的动力学控制方程之中。这样，在计算列车车轮跳轨全过程时，必须分别建立3种不同的动力学控制方程，分别为轮轨密贴时方程、轮轨分离时方程和轮轨冲击时方程。

2 计算方法

2.1 车辆振动分析模型

采用二轴车辆竖向振动分析模型，如图2所示。将车辆视为由1 个车体、2 个轮对以及车体和轮对之间的悬挂组成的多刚体系统，其中，车体视为质量为mc和绕其质心转动惯量为Jc的刚体，其自由度为质心处的竖向位移yc和转角θc；车体与轮对之间的悬挂弹簧刚度与阻尼系数分别为kv和cv；每个轮对质量为mw，后、前轮对的竖向位移分别为yw1和yw2；Lc为车辆定距之一半；v为车速。假定车辆向下的位移和顺时针转角为正向，其位移从各自静平衡位置处开始测量。

图2 二轴车辆及轨道振动分析模型Fig.2 Two-axle vehicle and track vibration analysis model

2.2 轨道振动分析模型

考虑两层支承的轨道竖向振动分析模型如图2所示，其中，钢轨视为弹性点支承的Bernoulli−Euler 梁，总长为L，并将相邻两支承点之间划分为1 个梁单元，单元长为l；轨枕视为质量为ms的单自由度刚体，其竖向位移为ys；钢轨与轨枕之间的线性弹簧刚度和黏滞阻尼系数分别为krs和crs；道床的线性弹簧刚度和黏滞阻尼系数分别为ksb和csb。从轨道左端到轮对的水平距离为xi(t)(i=1，2)，钢轨表面的竖向不平顺为r(x)。假定轨道向下的位移为正，转角顺时针方向为正向。

轨道节点与轨枕位移从左端依次排序，钢轨单元的形函数采用三次Hermite插值函数，如果以N表示单元形函数矩阵，qe表示单元节点位移矢量，ξ表示轮对与所在钢轨单元左节点之间的距离，那么，单元内任意一点在t时刻的竖向位移yr(ξ,t)可表示为

式中：N=(n1n2n3n4)；n1=1-3(ξ/l)2+2(ξ/l)3；n2=ξ[1-2(ξ/l)+(ξ/l)2]；n3=3(ξ/l)2-2(ξ/l)3；n4=ξ[(ξ/l)2-(ξ/l)]。

2.3 振动方程的建立及其求解

运用弹性系统动力学总势能不变值原理及形成矩阵的“对号入座”法则[1]，建立车辆−轨道系统振动方程。采用Wilson−θ逐步积分法，基于Fortran编制程序求解系统振动方程。

2.3.1 轮轨密贴阶段的控制方程

轮轨密贴时，轮对的位移不独立，后、前轮对的竖向位移yw1和yw2可表示为

轮轨密贴时的振动方程可表示为

式中，各分矩阵表达如下。

1)车辆的位移列阵Xv、钢轨的位移列阵Xr及轨枕的位移列阵Xs分别表示为：

其中：Xr中奇数项为节点位移，偶数项为节点转角；Nr为钢轨总自由度数；Ns为轨枕总自由度数。

2)车辆质量矩阵Mvv可表示为

钢轨质量矩阵Mrr可表示为

钢轨本身质量矩阵Mrr1(阶数为Nr×Nr)由钢轨单元质量矩阵(阶数为4×4)组集而成，mr为钢轨单位长度质量；受轮对影响引发的钢轨质量矩阵Mrr2(阶数为Nr×Nr)中的Ni表示轮对所在钢轨单元的形函数矩阵；ξi为轮对与所在钢轨单元左节点之间的距离；下标i=1,2，分别对应后轮对和前轮对；Ni(阶数为1×Nr)除轮对所在钢轨单元对应的4个元素外，其余元素为0。

轨枕质量矩阵Mss(阶数为Ns×Ns)可表示为

3)车辆刚度矩阵Kvv可表示为

钢轨刚度矩阵Krr可表示为

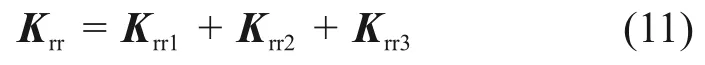
钢轨本身刚度矩阵Krr1(阶数为Nr×Nr)由钢轨单元刚度矩阵(阶数为4×4)组集而成，Er和Ir分别为钢轨弹性模量和钢轨截面对水平轴的惯性矩，N′和N″分别为N对局部坐标ξ的一次导数和二次导数；Krr2(阶数为Nr×Nr)和Krr3(阶数为Nr×Nr)分别为车辆和扣件刚度引起的钢轨刚度矩阵，后者对角线上除第1个和最后1个奇数外，每个奇数位置对应的元素为krs。

车辆与钢轨相互作用刚度矩阵Kvr(阶数为2×Nr)和Krv(阶数为Nr×2)的表达式为：

其中：

Kvr1和Krv1分别为后轮对与钢轨相互作用刚度矩阵；Kvr2和Krv2分别为前轮对与钢轨相互作用刚度矩阵。

轨枕的刚度矩阵Kss(阶数为Ns×Ns)可表示为

钢轨与轨枕相互作用刚度矩阵为Ksr(阶数为Ns×Nr) 与Krs(阶数为Nr×Ns)。Krs=，刚度矩阵Krs(阶数为Nr×Ns)中除第2i+ 1 行、第i列(i=1,2,…,Ns)外，位置对应的元素为-krs，其余均为0。

4)车辆阻尼矩阵Cvv可用cv代替Kvv中的kvv获得。

钢轨阻尼矩阵Crr可表示为

车辆与钢轨相互作用阻尼矩阵Cvr(阶数为2×Nr)和Crv(阶数为Nr×2)的表达式为：

Cvr1和Crv1分别为后轮对与钢轨相互作用阻尼矩阵；Cvr2和Crv2分别为前轮对与钢轨相互作用阻尼矩阵。

轨枕的阻尼矩阵Css(Ns×Ns)可表示为

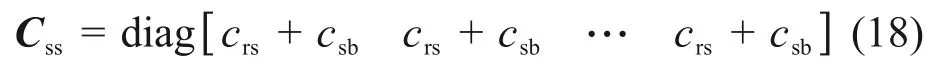
钢轨与轨枕相互作用阻尼矩阵为Csr(阶数为Ns×Nr)和Crs(阶数为Nr×Ns)。Crs=，用crs代替Krs中的krs可得Crs。

5)车辆的荷载列阵Fv可表示为

钢轨的荷载列阵Fr(阶数为Nr×1)可表示为

2.3.2 轮轨分离阶段的控制方程

对于车轮跳轨阶段，车轮与钢轨已经分离，共有以下3种情况：前轮对跳轨，后轮对密贴；后轮对跳轨，前轮对密贴；前、后轮对同时跳轨。以下介绍不同情况下的轮轨分离阶段的车辆−轨道系统振动控制方程。

1)对于一个轮对跳轨、另一个轮对密贴的情况，其振动方程相似，这里仅以前轮对单独跳离钢轨为例介绍。当前轮对跳离钢轨且后轮对密贴时，前轮对的位移yw2独立，后轮对的竖向位移yw1不独立，系统振动方程在密贴的基础上发生变化，可表示为

式中，车辆位移列阵、质量矩阵和刚度矩阵可表示为：

注意，将中的kv替换为cv，即得车辆振动阻尼矩阵。

钢轨质量矩阵、刚度矩阵和阻尼矩阵可表示为

车辆与钢轨相互作用刚度矩阵和及阻尼矩阵和可表示为：

车辆荷载列阵和钢轨荷载列阵可表示为

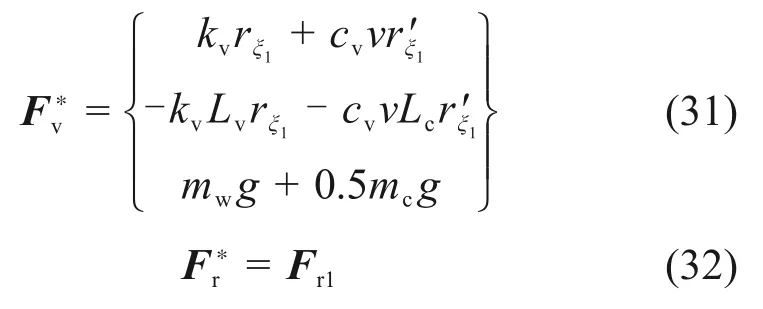
2)当前轮对与后轮对同时跳离钢轨时，前、后轮对的竖向位移yw2和yw1均独立，车辆系统振动方程可表示为

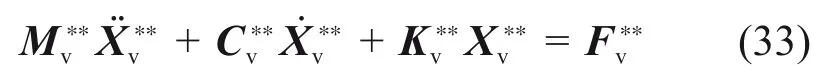
式中：车辆位移列阵、质量矩阵、刚度矩阵及车辆荷载列阵可表示为：

同时，车辆振动阻尼矩阵可通过将中的kv替换为cv获得。

轨道振动方程可表示为

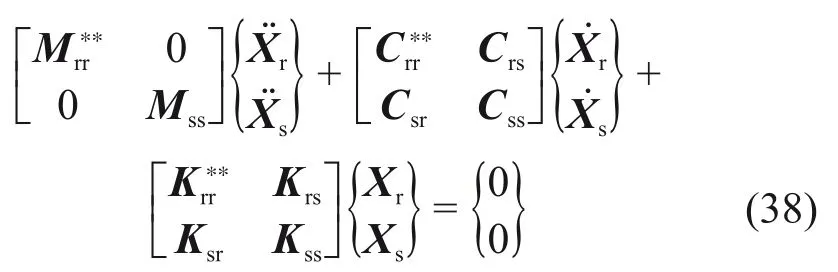
钢轨质量矩阵、刚度矩阵和阻尼矩阵可表示为：=Mrr1；=Krr1+Krr3；=Crr2。

2.3.3 轮轨冲击阶段的控制方程

由图1(a)可见：在t2时，轮轨从分离阶段进入密贴阶段，此时，车轮位移等于钢轨位移与轨道不平顺之和，轮轨相对位移量值为零。然而，此时，并不能保证轮轨相对速度也为零，这意味着轮轨之间会出现速度差值，必然引起轮轨冲击，如图1(b)所示。这里仅以前轮对冲击、后轮对密贴为例来介绍轮轨冲击阶段的计算方法，此时，振动方程可表示为

车辆荷载列阵和钢轨荷载列阵的表达式如下：

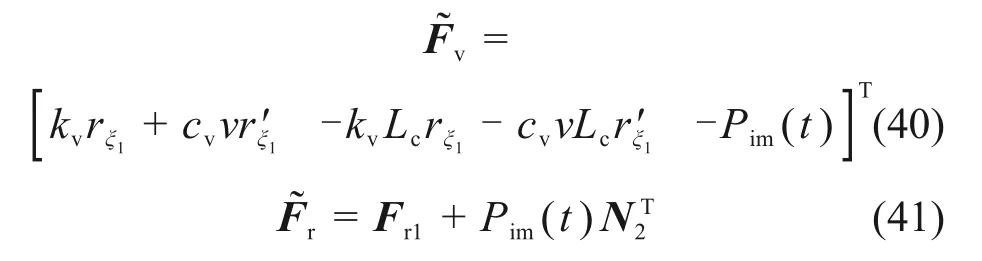
其中：Pim(t)为冲击力。

鉴于轮轨冲击力的计算比较复杂，本文把它视为优化问题并采用迭代算法完成计算，具体计算步骤如下。

第一步：假定冲击力函数Pim(t)如图1(b)所示，具体表达式为

式中：p1(t)和p2(t)为假定的作用力函数，可以是线性的，也可以是非线性的；pim为最大冲击力幅值；pc0为冲击终端时的幅值，其特点是应与后续轮轨正常密贴时的轮轨力幅值相当；t1为跳轨起点；t2为冲击起点；Δt为冲击时间；t2+ Δt为冲击终点；β为小于1的正数。

第二步：假定控制变量为pim，pc0和Δt。

第三步：建立目标函数，并以t2+ Δt时刻的轮轨相对速度表示。建立目标函数如下：

式中：为车轮速度；为钢轨随时间t变化的速度；为钢轨随距离x变化的速度；x2(t2)为t2时刻轮轨接触点距离轨道计算起点的距离；为轨道不平顺随距离变化的速度。

第四步：分别建立冲击终点t2+ Δt时刻的轮轨相对位移、轮轨相对速度及轮轨力的约束条件[14]，即轮轨相对位移为零或为很小的数值、轮轨相对速度为零或为很小的数值、轮轨力与轮轨正常密贴时的轮轨力相当。

轮轨相对位移约束条件如下：

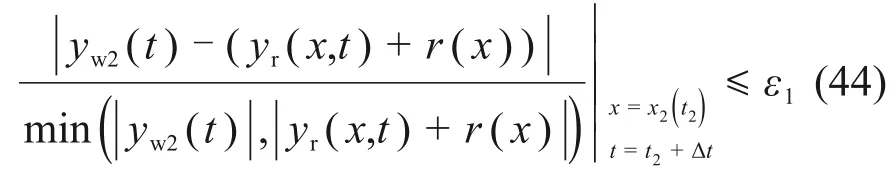
当yw2(t2+ Δt) > 0，yr(x2(t2)，t2+ Δt) +r(x2(t2)) > 0时，

当yw2(t2+ Δt) < 0，yr(x2(t2)，t2+ Δt) +r(x2(t2)) < 0时，

当yw2(t2+ Δt) > 0，yr(x2(t2)，t2+ Δt) +r(x2(t2)) < 0时，

关于轮轨相对速度约束条件如下：

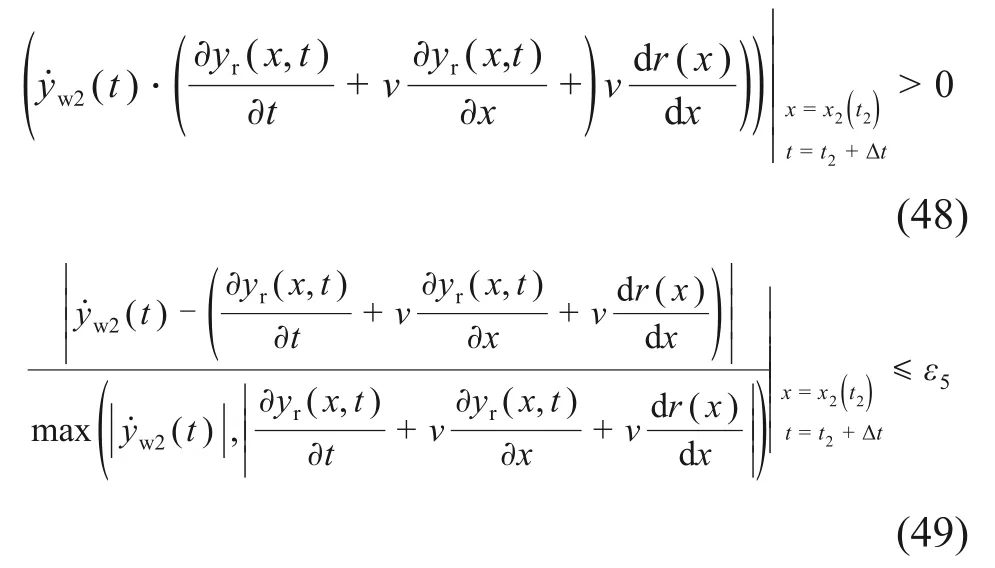
另外，轮轨力约束条件如下：

式(44)～(50)中的εi(i=1,2,…,6)为较小的正数，用以控制计算精度；pc2为前轮对实际轮轨力，可表达为

第五步：满足所有的约束条件且使目标函数达到最小值时的3 个控制变量pim，pc0和Δt即为所求，从而最终可以确定轮轨冲击力Pim(t)。

3 计算实例及其分析

二轴车辆模型参数如表1所示，轨道模型参数如表2所示。选取波长λ为0.8 m、波幅a为2 mm的轨面单一谐波型不平顺作为跳轨诱因，并且设置于轨道中间部位，具体表达式如下：

轮轨冲击力函数假定如下：

式中：β取0.5。同时，用以控制计算精度的参数取值为ε1=ε2=ε3=ε5=ε6=0.05，ε4=10-5m。

取轨道计算长度L=72 m，分别计算车辆以速度80，90 和100 km/h 通过轨道时的车轮跳轨全过程。为了符合习惯，图3(a)和图4中符号取向上为正，其他图中的符号与前述模型图中的坐标方向一致。

表1 二轴车辆模型参数Table 1 Two-axle vehicle model parameters

图3(a)所示为当车辆以速度90 km/h 通过该轨道不平顺时，前轮对车轮跳轨高度时程曲线。由图3(a)可知：当车辆运行至t1=0.403 s 时，轮轨开始分离，车轮开始起跳，并且一直上升；当tz=0.408 s时，车轮跳轨高度达到最大值hmax=5.52 mm，之后，车轮开始下降；当t2=0.412 s 时，车轮回落到钢轨之上。由此可见，车轮跳轨高度时程曲线，反映了跳轨车轮位移的基本特征，即车轮开始起跳、车轮上升、车轮下降、轮轨再次密贴。

表2 轨道模型参数Table 2 Track model parameters

图3 车速为90 km/h时的时程曲线示意图Fig.3 Schematic diagram of time histories when vehicle velocity is 90 km/h

图3(b)所示为当车辆以速度90 km/h 通过式(52)表示的轨道不平顺时，前轮对轮轨力时程曲线。由图3(b)可知：当车辆运行至t1=0.403 s 时，轮轨力为零，表示轮轨开始分离；当t2=0.412 s时，车轮经过跳轨阶段后重新回落到钢轨之上，但是，由于此时车轮竖向速度=0.411 m/s，钢轨竖向速度=0.004 m/s，二者之间出现了相对速度，必然引起轮轨冲击作用，冲击时间Δt=9.0 ms，冲击过程中的最大值pim=386.2 kN；当t2+ Δt=0.421 s 时，轮轨冲击结束，重新开始正常状态下的轮轨密贴。由此可见，轮轨力时程曲线反映了跳轨车轮轮轨力的基本特征，即轮轨密贴、轮轨分离、轮轨冲击及轮轨再次密贴。特别地，从t2至t2+ Δt，虽然轮轨处于密贴阶段，但轮轨之间存在冲击作用，在列车车轮跳轨全过程计算中，必须考虑到这一因素，否则，对t2时刻之后的车−轨系统振动响应将会失真。

由此可见，本文提出的计算方法从本质上揭示了列车车轮跳轨全过程，能够描述车轮跳轨的关键信息，如跳轨高度、跳轨时间、跳轨姿态、轮轨冲击力幅值、冲击时间等。

图4所示为车辆分别以速度80，90，100 km/h通过轨道不平顺(见式(52))时，前轮对跳轨高度时程曲线，其中，与分别表示车速80 km/h时跳轨时间起点与终点，与分别表示90 km/h时的跳轨时间起点与终点，与分别表示车速100 km/h 时的跳轨时间起点与终点，，与分别表示车速80，90和100 km/h时的跳轨高度最大值；同一车速下的跳轨终点时刻与起点时刻的差值表示车轮跳轨持续时间，其中，=0.363 s，即速度越高，车轮跳轨持续时间越长；即速度越高，车轮跳轨高度越高。

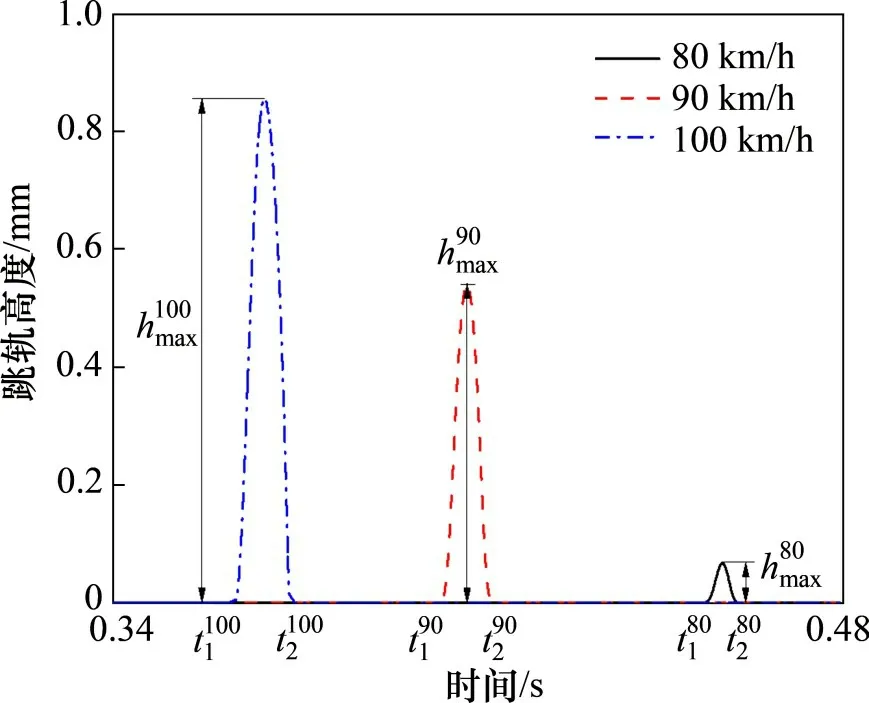
图4 不同速度条件下的车轮跳轨高度时程曲线Fig.4 Time history of wheel-jumping height under different speeds

为了探究是否考虑轮轨冲击作用对于车−轨系统振动响应的影响程度，以车速90 km/h为例，当车辆通过式(52)表示的轨道不平顺时，分别考虑轮轨冲击和不考虑轮轨冲击，计算车体加速度、钢轨速度、钢轨加速度、轨枕速度和轨枕加速度等振动响应时程曲线，如图5～7所示，其中，红色实线表示考虑轮轨冲击作用时的结果，蓝色虚线表示不考虑冲击时的结果。

图5所示为车体加速度时程曲线局部图。由图5可见：在t2=0.412 s 至t2+ Δt=0.421 s 期间，考虑冲击时的车体加速度最大幅值为4.25 m/s2，不考虑冲击时的车体加速度最大幅值为0.71 m/s2，并且考虑冲击时的车体加速度曲线幅值普遍远大于不考虑冲击时的车体加速度曲线幅值，同时，考虑冲击时的车体加速度振动频率也远高于不考虑冲击时的车体加速度振动频率。可见，是否考虑轮轨冲击对于车体振动加速度影响很大。

图5 v=90 km/h、考虑与不考虑冲击时的车体加速度时程曲线Fig.5 Time histories of car body acceleration considering wheel-rail impact or not when v=90 km/h

图6(a)所示为前轮对作用点下的钢轨速度时程曲线局部图。由图6(a)可见：从t2=0.412 s 开始，是否考虑轮轨冲击作用导致钢轨速度时程曲线发生了很大差异，主要表现在振动幅值和相位，其中，考虑冲击时的钢轨最大速度为0.410 m/s，不考虑冲击时的钢轨速度为0.225 m/s，前者是后者的约1.82 倍；另外，二者曲线的相位几乎为反相位状态。

图6(b)所示为前轮对作用点下的钢轨加速度时程曲线局部图。由图6(b)可见：从t2=0.412 s开始，考虑冲击时钢轨最大加速度为−362.188 m/s2，不考虑冲击时的钢轨最大加速度为78.205 m/s2，前者是后者的约4.63 倍，同时，在t2+ Δt=0.421 s 之后的二者曲线相位几乎呈反相位状态。

由此可见，图6充分表明是否考虑轮轨冲击，对于钢轨速度及加速度影响甚大。

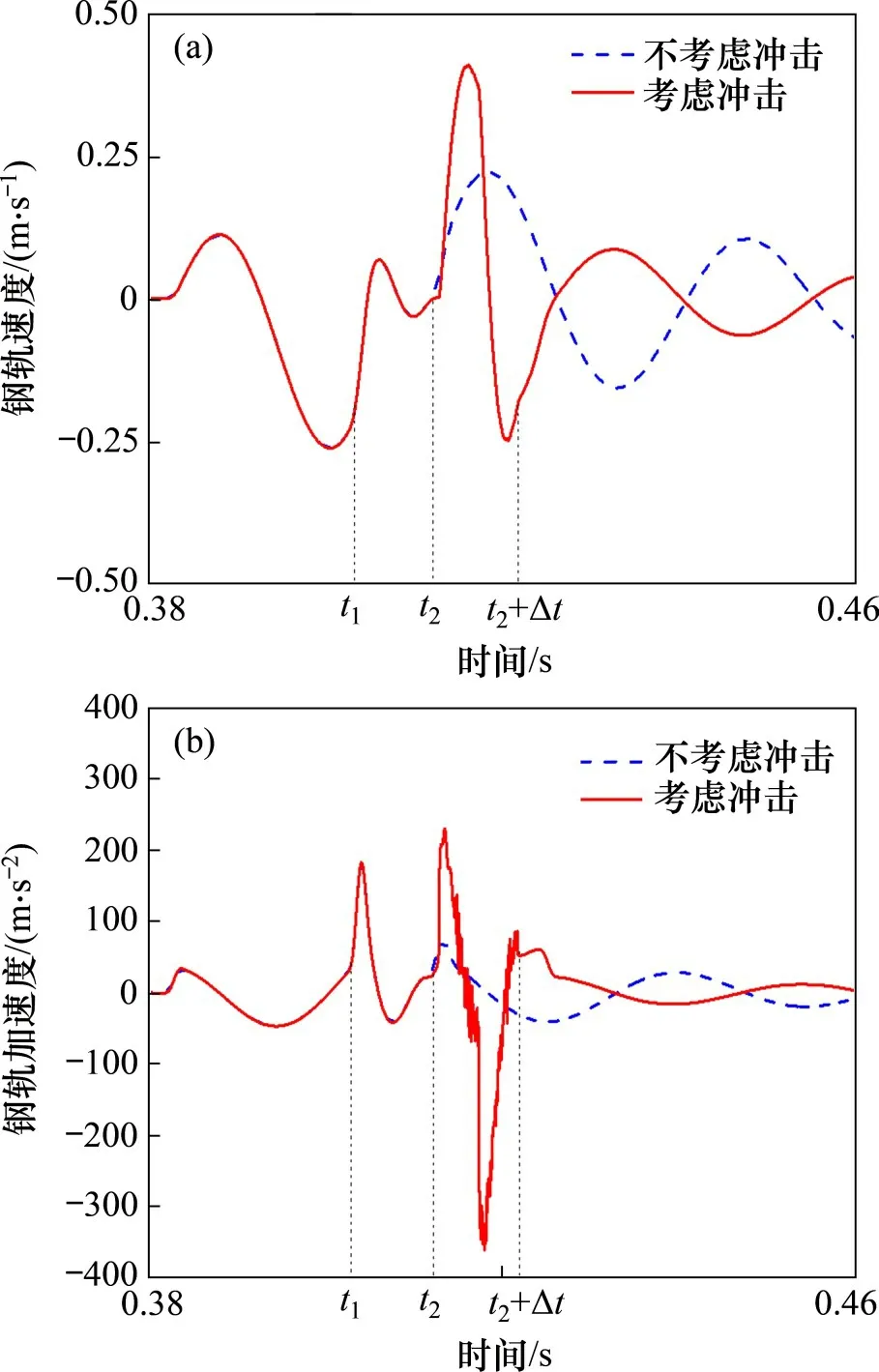
图6 v=90 km/h、考虑冲击与不考虑冲击前轮对作用点下钢轨的时程曲线Fig.6 Time history of rail under action point of front wheelset considering impact or not when v=90 km/h

图7(a)所示为计算长度中点处的轨枕速度时程曲线局部图。由图7(a)可见：从t2=0.412 s 开始，考虑冲击时轨枕最大速度为0.113 m/s，不考虑冲击时的轨枕最大速度为0.043 m/s，前者是后者的约2.63 倍；同时，在t2+ Δt=0.421 s 之后的二者曲线相位几乎为反相位状态。

图7(b)所示为计算长度中点处的轨枕加速度时程曲线局部图。，由图7(b)可见：从t2=0.412 s 开始，考虑冲击时钢轨最大加速度为−97.490 m/s2，不考虑冲击时的钢轨最大加速度为18.045 m/s2，前者是后者的约5.40 倍；同时，在t2+ Δt=0.421 s 之后的二者曲线相位也有了很大差异。

由此可见，图7也充分表明是否考虑轮轨冲击对于轨枕速度及加速度影响很大。