基于堆积实验的小米离散元参数标定

王志鹏 李永祥 徐雪萌

(河南工业大学机电工程学院，郑州 450001)

随着离散元理论及仿真技术不断发展与完善，离散元法(DEM)在农业装备工程应用也日益广泛[1]。利用离散元法全面系统地研究小米离散元仿真接触参数，有利于探究小米颗粒流流态化运动机理，进一步提高小米农业装备的工作效率，使其达到理想的工作速度、精度。为使仿真实验更加接近实际，需在离散元仿真实验中设定精确仿真接触参数，保证离散元仿真的精度[2]。关于散体颗粒参数标定已有大量的研究工作[3，4]，李永祥等[5]基于颗粒缩放理论和响应面优化实验，以小麦粉颗粒堆积角为响应值，通过相关实验放大颗粒的小麦粉仿真接触参数进行了标定；于庆旭等[6]基于粘结模型，通过堆积实验法结合台架实验和仿真实验建立三七种子离散元模型，标定三七种子与 ABS 塑料之间接触参数。王美美等[7]基于响应面优化实验，以玉米籽颗粒堆积角为响应值，利用中心组合设计对玉米籽粒进行仿真参数标定。但运用离散元理论对小米颗粒进行仿真实验标定的系统性研究相对较少。

由于小米颗粒间各向异性及相互作用的复杂性，为获取小米在离散元中精确的仿真接触参数，有必要对仿真接触参数进行重新标定[8]。本研究以小米颗粒为对象，基于小米颗粒实体堆积实验，结合离散元法“Hertz-Mindlin”颗粒接触模型，构建小米颗粒仿真模型，以小米颗粒休止角为响应值；基于Plackett-Burman 实验、最陡爬坡实验、Box-Behnken 实验对小米颗粒的仿真接触参数进行实验标定，得到接触参数的最佳组合，并对其最佳组合参数进行实验验证，以期为小米等其它颗粒离散元仿真提供参考。

1 材料与方法

1.1 实验材料

小米：蛋白质17%、脂肪4%、碳水化合物25%、平均粒径1.5 mm。

1.2 离散元理论

1.2.1 离散元的基本原理

离散元理论(DEM)是一种通过实时更新颗粒与颗粒间及颗粒与环境间相互作用的运动状态和力学特性解决散粒体介质的数值模拟方法，广泛应用于散粒体和粉体工程领域[9]。离散元法的原理是将整体研究对象划分为相互独立的微型单元，根据各单元间的相互作用及牛顿运动定律，运用动静态松弛法等迭代方法实现微型单元的循环迭代计算，并根据实时的所有单元受力与位移来更新单元的位置，通过对其单元的微观运动来研究对象的宏观规律[10]。

1.2.2 离散元理论接触模型

目前，离散元理论研究对象一般为散粒体，因此颗粒接触模型的接触力学对离散元理论非常重要。对于不同的仿真对象可以根据具体的使用范围来确定相应的仿真模型[11]。

Hertz-Mindlin是 EDEM软件系统的自身默认模型,当颗粒半径为R1和R2的散粒体产生弹性接触时，则有法向重叠量α为[12]：

(1)

(2)

R*为颗粒的等效颗粒直径，由式(3)推出[12]：

(3)

颗粒间法向力Fn为[12]：

(4)

E*为等效弹性模量，由式(5)推出[12]：

(5)

式中：E1和E2分别为颗粒1和2的弹性模量，GPa；v1和v2分别为颗粒1和2的泊松比；颗粒间切向力Ft为[12]：

(6)

式中：δ为切向重叠量；G*为等效剪切模量，由式(7)推出：

(7)

式中：G1和G2分别为颗粒1和颗粒2的弹性模量；v1和v2分别为颗粒1和颗粒2的泊松比。

考虑到颗粒间摩擦力的影响，散粒体产生切向滑动与滚动的极限判断公式为[13]：

(11)

本实验仿真物料颗粒为小米，颗粒之间黏性力较小，利用系统默认“Hertz-Mindlin无滑动接触模型”来进行仿真模拟。

2 参数标定过程

2.1 物理模型

根据休止角的相关研究[14]，实验参照GB/T 16913.5—1997，采用注入法对小米休止角进行测量，漏斗下口内径为10 mm，锥度为60°，圆柱底盘直径D为100 mm，漏斗下端口距圆柱底盘上表面距离75 mm，测量装置如图1所示。在测量之前，将小米颗粒从漏斗上方缓慢倒入漏斗，同时使用玻璃棒轻微搅动，避免小米漏斗出口发生堵塞，当底盘边缘溢出小米后，停止向漏斗添加小米，直到颗粒的堆积高度无变化时，使用钢尺对小米颗粒堆积高度H进行测量。根据式(12)计算小米颗粒的休止角，重复测量5次取其平均值，测得小米休止角为30.17°。

(12)

图1 小米颗粒堆积实验

2.2 仿真模

2.2.1 仿真参数

结合软件内置数据库对颗粒与不锈钢离散元仿真进行参数设置，本研究所用仿真参数如表1所示[14]。

表1 离散元仿真参数表

2.2.2 仿真模型

根据GB/T11986—98《表面活性剂粉体和颗粒休止角的测量》，采用注入法，漏斗出口内径d=10 mm，接收颗粒圆柱底面直径D=100 mm，漏斗下端口中心距圆柱底盘上表面75 mm，设置小米颗粒粒径d=1.5 mm；考虑到时间及计算机性能的限定，仿真采用软球模型[15]。颗粒生成方式设为 Dynamic，生成速率设为 2 000个/s，待小米颗粒完全溢出后，使用软件后处理的Protractor 功能，通过Enable 中的 Manually Define标记小米的颗粒位置测量休止角。

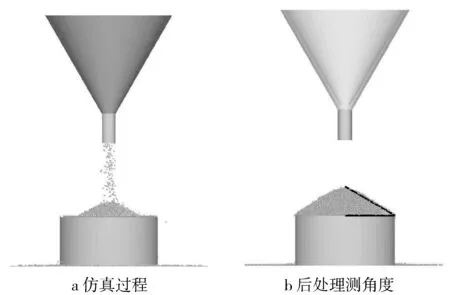
图2 小米颗粒堆积的模拟仿真

2.3 仿真参数的响应面设计

2.3.1 Plackett-Burman 实验

Plackett-Burman 实验以小米休止角为响应值，通过考察小米休止角与各仿真参数间关系，筛选对小米颗粒仿真接触参数的显著性,参数如表2所示。

表2 Plackett-Burman 实验参数列表

实验设计与最终结果如表3所示，运用Design Expert 软件功能对其实验结果进行显著性的比较分析，从而得到各个仿真接触参数的显著性如表4所示。小米-小米静摩擦系数、小米-小米滚动摩擦系数、小米-不锈钢静摩擦系数对小米颗粒休止角的影响极其显著；但其余仿真接触参数对小米颗粒休止角的测定影响相对较小显著。影响较小的其余参数根据相关参考文献进行取值[16]：(小米-小米恢复系数0.20、小米-小米静摩擦系数0.60、小米-不锈钢恢复系数0.20、小米-不锈钢滚动摩擦系数0.25)，结合其他仿真接触参数来进行最陡爬坡实验及响应面实验设计。

表3 Plackett-Burman 实验设计及结果

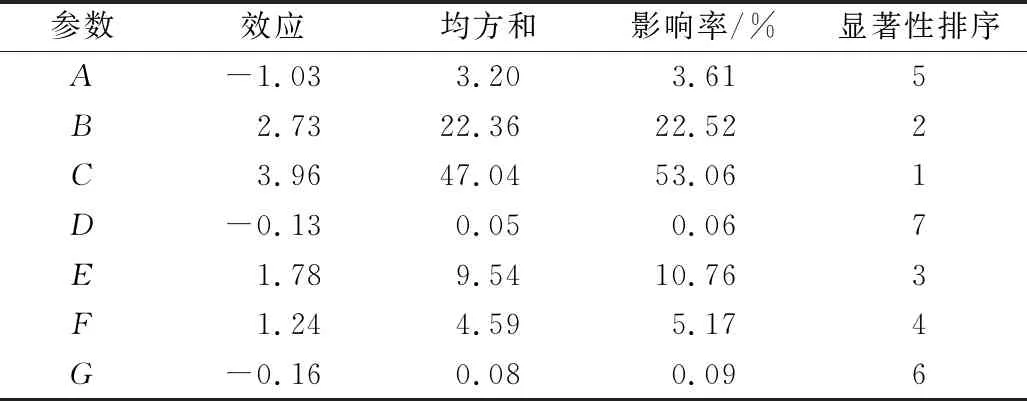
表4 Plackett-Burman 实验参数显著性分析

2.3.2 最陡爬坡实验

基于Plackett-Burman 实验结果，筛选出显著性较强的仿真接触参数，并设计最陡爬坡实验，本次最陡爬坡实验通过从PB实验中心点开始得到的回归系数来确定爬坡步长，爬坡步长通常取较大值，以便可以快速逼近目标最优值。如表5所示：在4号水平中休止角产生的相对误差是最小，在1号到5号水平区间，休止角产生的相对误差趋势是由大变小再变大再变小，故以4号水平为中心位置点，3号和5号水平为低、高水平来对后面的响应面设计。

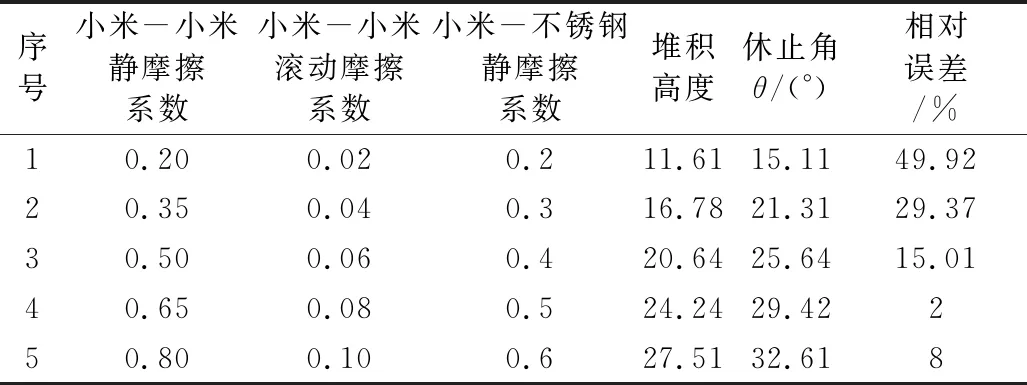
表5 最陡爬坡实验结果

2.3.3 Box-Behnken 实验

根据最陡爬坡实验结果及响应面实验设计原理，分别将筛选的显著性参数进行排序为低、中、高3 水平，以此3水平来进行实验设计，同时选取3 个中心点评估判断误差对。设计结果如表6所示，运用Design-Expert软件计算出小米颗粒休止角与显著性较强参数的二阶回归方程为：

θ=78.73+16.28A-282.86B-189.31C+83.33AB+45.83AC+440BC-29.69A2+473.96B2+121.71C2

(13)

根据原有模型剔除对休止角影响相对较小的参数项(AB、B2)，在模型优化回归方程后对其进行分析，结果如表8所示，失拟项P=0.327 9；变异系数CV=1.04%；决定系数R2=0.981 7；校正决定系数AdjustedR2=0.963 5；预测决定系数PredictedR2=0.903 2；实验精密度Adep Precision=27.408 4。优化后回归方程为：

表6 Box-Behnken实验设计及结果

θ=70.84+23.79A-152.88B-187.85C+45.83AC+440BC-30.33A2+120.25C2

(14)

表7 Box-Behnken 实验优化回归模型结果

2.3.4 回归模型交互效应分析

根据优化回归模型方差分析结果，可知小米与小米静摩擦系数-小米与不锈钢静摩擦系数(AC)及小米与小米静摩擦系数-小米与不锈钢滚动摩擦系数(BC)的P<0.01，这两个交互项对小米休止角影响极其显著。在小米-小米滚动摩擦系数(A)为0.60以及小米-小米滚动摩擦系数(B)为0.08以及两种情况下，应用 Design-Expert 软件对小米与小米静摩擦系数-小米与不锈钢静摩擦系数(AC)及小米与小米静摩擦系数-小米与不锈钢滚动摩擦系数(BC)交互作用的三维响应曲面进行绘制，可以直观反映交互项对休止角的影响。结果表明，相对于小米与不锈钢滚动摩擦系数(C)，小米与小米静摩擦系数(A)和小米与小米滚动摩擦系数(B)的效应面曲线比较陡，表明其对休止角影响较为显著。

3 最佳参数组合的确定及验证

运用Design Expert软件，以小米实际休止角为目标，由优化产生的回归方程结果可知，欲使仿真与实验所得休止角误差最小，则小米-小米静摩擦系数应为0.602，小米-小米滚动摩擦系数为0.08，小米-不锈钢静摩擦系数为0.424。用最佳参数组合仿真测定小米颗粒的休止角，仿真实验结果与实体测定值相比较，如图4所示。仿真实验所得休止角为29.95°，与实体测定值误差值为0.73%，证明仿真实验结果与实体测定值无显著性差异。

图3 仿真实验与物理实验对比

4 结论

基于小米颗粒实体堆积实验和离散元法Hertz-Mindlin无滑动接触模型，对小米颗粒的接触参数进行标定。由 Plackett-Burman 实验选取对小米颗粒休止角影响显著的因素为：小米-小米静摩擦系数、小米-小米滚动摩擦系数、小米-不锈钢静摩擦系数。

基于 Box-Behnken 实验结果，建立并优化显著性仿真接触参数和休止角之间的二阶回归模型，方差分析可知，除了 3 个显著性参数的一次项外，小米与小米静摩擦系数-小米与不锈钢静摩擦系数(AC)、小米与小米滚动摩擦系数-小米与不锈钢静摩擦系数(BC)对小米颗粒休止角影响也极其显著。

以小米实际休止角为目标，对回归方程进行寻优求解，得到显著性最佳参数组合为小米-小米静摩擦系数为0.602、小米-小米静摩擦系数为0.8小米-不锈钢静摩擦系数为0.424;以最佳参数组合对休止角进行仿真实验，仿真实验结果与实体测定值无显著差异。结果表明，基于颗粒堆积实验标定所得到的仿真接触参数可用于小米离散元仿真。