基于被引频次对数矫正的影响因子及其学科标准化研究

刘雪立，郭 佳，申 蓝，王 燕，盛丽娜，方红玲，李建华，丁 君

（1. 新乡医学院期刊社/河南省科技期刊研究中心，新乡 453003；2. 新乡医学院管理学院，新乡 453003）

1 引 言

长期以来，由于全球性SCI 现象和影响因子崇拜[1]，导致影响因子被广泛滥用[2]和误用[3-4]，甚至将评价期刊的影响因子用于评价研究者个人[5]。而影响因子被滥用和误用的根源在于其自身设计的缺陷，最显而易见和被关注较早的缺陷是影响因子的计算违背了统计学原理，用平均数指标表征呈现偏态分布的期刊中各论文被引频次的总体水平[6-7]，并且影响因子的计算由于未考虑学科之间的巨大差异，无法应用于学术期刊的跨学科评价[8]。然而，国内外广泛应用期刊影响因子进行学术评价，甚至经常将影响因子应用于跨学科学术评价。例如，在德国的大学里，通常把科学家发表论文的期刊的影响因子加在一起，以此确定部门的研究基金；在芬兰，政府用于资助大学医院的基金，在一定程度上依赖于研究者发表论文期刊的影响因子[9]；Oelrich等[10]以欧盟15 个成员国为研究对象，把各国家发表的每篇论文按其所在期刊的影响因子相加，作为该国的累计影响因子，以此对各个国家研究绩效进行评价；在我国大学发布的职称晋升、科研奖励、人才评价等文件中，广泛采用影响因子作为评价标准。

2020 年2 月20 日，我国教育部、科技部联合印发了《关于规范高等学校SCI 论文相关指标使用树立正确评价导向的若干意见》（以下简称“《意见》”），引起学术界广泛关注[11-12]。该《意见》发布的目的不是要废除SCI 论文及其相关评价指标，而是强调要“规范使用”，最大限度地纠正对影响因子的滥用和误用。因此，本研究针对影响因子的重要缺陷，在对科技期刊论文被引频次偏态分布进行正态性转换的基础上计算各期刊影响因子，再进行学科标准化处理，使期刊影响因子的学科标准化更加科学合理，为规范使用影响因子奠定科学基础。

2 期刊影响因子学科标准化研究现状

众所周知，不同学科论文被引频次和期刊影响因子存在明显差异，例如，Mingers 等[13]指出，在管理学科领域，战略管理类论文的被引频次近4 倍于公共管理类论文，生物科学领域期刊影响因子远高于数学期刊[14]，纳米科学与技术期刊影响因子是历史学期刊影响因子的近10 倍[15]。为了实现学术期刊的跨学科评价，有研究者很早之前就开始了对影响因子学科标准化研究，标准化的方法主要包括相对影响因子（relative impact factor，rIF）、期刊影响因子分区、期刊影响因子百分位（journal impact factor percentile，JIFP）三个方面，具体阐述如下。

2.1 相对影响因子

相对影响因子是指以某期刊影响因子除以该期刊所在学科期刊影响因子的特征值（主要指该学科期刊影响因子的最大值、平均值、中位数等）。这方面研究开始最早，也是最直接的影响因子学科标准化方法。1992 年，Sen[16]提出，以某期刊影响因子除以该期刊所在学科期刊影响因子最大值作为期刊rIF。2016 年，Logan[17]再次强调，采用该方法对期刊影响因子进行学科标准化。1996年，Marshakiva-Shaikevich[18]提出，用某期刊影响因子除以该期刊所在学科前5 种期刊影响因子的平均值的学科标准化方法。国内学者熊晓英[19]、杨兵等[20]先后提出，用某期刊影响因子除以该期刊所在学科全部期刊影响因子的平均值作为相对影响因子。刘雪立等[21]尝试采用某期刊影响因子除以该期刊所在学科中位影响因子、集合影响因子进行学科标准化处理。

由于不同学科期刊影响因子值的分布千差万别，几乎全部未呈现出正态分布[22]，以期刊影响因子除以学科影响因子的最大值、中位值、平均值或集合影响因子等，进行学科标准化处理会产生明显不同的结果，且不具有科学性。例如，若某学科排在第一位的期刊影响因子特别高，采用期刊影响因子除以学科最大影响因子计算相对影响因子，则该学科其他期刊的相对影响因子将明显低于其他学科期刊相对影响因子。Abramo 等[23]认为，采用各期刊影响因子除以学科平均影响因子或中位影响因子进行学科标准化是徒劳的。

2.2 期刊影响因子分区

1999 年，邹承鲁院士在《科学时报》上首次提出按照影响因子高低将某学科期刊分成高、中、低3 区；2001 年，中国科学院文献情报中心首次发布了期刊分区办法（中科院分区），将SCI 期刊分为4个分区[24]，目的是对不同学科期刊影响因子进行学科标准化处理，同一分区的期刊在各自学科具有大致相同的地位和影响力，使得不同学科期刊具有了一定的可比性。

2009 年2 月，期刊引证报告（Journal Citation Reports，JCR） 中增加了从2003 年至今的期刊分区，具有科学性和客观性[25]，JCR 数据库同样将期刊分为4 个分区：Q1 区是IF 排名前25%的期刊，Q2 区为IF 排名前25%～50%的期刊，Q3 区为IF 排名前50%～75%的期刊，Q4 区为IF 排名最后25%的期刊[26-27]。

期刊分区实现了简单的学术期刊跨学科评价，相当于定性分级评价，每一分区（JCR 分区）内约有2500 种期刊，即使同一学科相同分区内也有许多期刊，而这些期刊的影响因子差别也很大。因此，要实现精准的学术期刊跨学科评价，期刊分区是无能为力的。

2.3 期刊影响因子百分位

2004 年，Pudovkin 和Garfield[28]提出了排序标准化影响因子（rank-normalized impact factors，rnIF），其计算公式为

其中，K表示某学科期刊总数；R表示某期刊影响因子在相应学科降序排列的位次。显然，同一学科内期刊排名越靠前，rnIF 值越大，这是期刊影响因子创建者Garfield 直接参与的影响因子学科标准化。2015 年，JCR 中新增了一个文献计量学评价指标：期刊影响因子百分位，其计算公式为

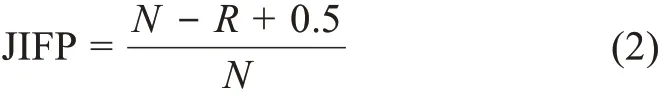
其中，N表示某学科期刊总数；R表示该学科某期刊影响因子降序排列的位次。分子中增加一个0.5，其作用是避免当R=N时（即每个学科排名最后一位期刊）JIFP=0 的情况发生。公式(2)几乎完全继承了公式(1)的影响因子学科标准化设计理念，只是分子中附加的常数由1 变更为0.5，这对计算结果的影响更小。rnIF 和JIFP 含义几乎一样，主要表征某期刊影响因子在所属学科的排序位置，目的是对不同学科期刊的跨学科评价设置一个完全定量的评价指标[29]。俞立平[30]详细介绍了JIFP 指标的特点，其认为JIFP 的最大优点是通过标准化变换，得出了学科内每一期刊的相对位置，以方便不同学科之间的比较。

然而，JIFP 指标同样存在明显缺点，从公式(2)可以看出，不同学科内影响因子排序相同的期刊，其JIFP 的大小完全由学科内期刊总数来决定，从而导致小学科的优秀期刊被低估，大学科的优秀期刊可能被高估。另外，JIFP 指标只考虑了期刊影响因子排序，而忽视了影响因子数值差异程度[29]。

3 对数矫正影响因子及其学科标准化的设计

3.1 对数矫正影响因子设计的理论基础

上文中提到的期刊影响因子分区和JIFP 属于位置指标，主要是由期刊影响因子在各自学科内排序位置决定的，两者共同的缺陷是忽视了期刊实际影响力的差异程度。例如，交叉学科（multidisci‐plinary）共有64 种期刊（JCR-2018），排在前3 位的期刊依次是Nature、Science和Nature Communication，三者2018 年影响因子分别为40.137、37.205和12.124，三者的JIFP 分别为99.219、97.656 和96.094，均属于Q1。无论Nature Communication影响因子是高还是低，只要排在第3 位，其JIFP 都是96.094。相对影响因子是完全定量指标，但是由于影响因子实质上是某期刊前两年发表的文献在统计当年的篇均被引频次，然而，每种期刊论文被引频次均不呈现正态分布，用篇均被引频次作为期刊影响因子是违背统计学原理的。再者，绝大多数学科期刊影响因子的分布也未呈现正态分布，用某期刊影响因子除以其所在学科期刊平均影响因子、中位影响因子、集合影响因子及最大影响因子等计算相对影响因子，同样违背统计学原理，学科标准化的效果依然存在极大的不确定性。

众多学者[22,31-32]研究证实，对期刊论文被引频次取对数，可以将被引频次转换为正态分布或近似正态分布。楼文高等[33]研究证实，对论文被引频次开平方、开三次方和开四次方也能将被引频次分布转换为正态分布。目前，将期刊论文被引频次的偏态分布转换为正态分布不存在争议，无论取自然对数[34]还是以10 为底数的对数[31]，被引频次分布正态转换效果都很好。

本文对Geology杂志2016—2017 年发表的论文被引频次取对数后的数据分布（图1）进行研究，得出了同样结论。由图1 可以看出，期刊论文被引频次呈现明显的偏态分布（图1a），经过对数转换（无论对数的底数大小），都能将被引频次转换为近似正态分布，底数的大小对转换效果几乎没有影响。两年后的累计被引频次（Ct）和年度被引频次（C2018）对数转换效果也没有明显差异。同时，本文发现在选定的5 个学科中，论文被引频次对数转换后计算的影响因子也呈正态分布（见实证研究的结果与分析部分）。因此，用每个期刊的影响因子除以其所属学科所有期刊的平均影响因子进行学科标准化具备了科学性。

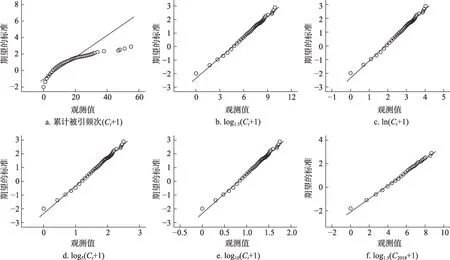
图1 Geology杂志2016—2017年论文被引频次对数转换前后的Q-Q图

3.2 学科标准化影响因子及其数学表达

对数矫正影响因子（IFlog）矫正了影响因子计算中直接使用论文篇均被引频次的统计学缺陷，并且本文选定的5 个学科期刊IFlog均呈正态分布。因此，以某期刊IFlog除以该期刊所在学科全部期刊IFlog的平均值作为学科标准化影响因子（category norml‐ized impact factor，cnIF）就具备了统计学上的合理性。cnIF 的数学表达式为

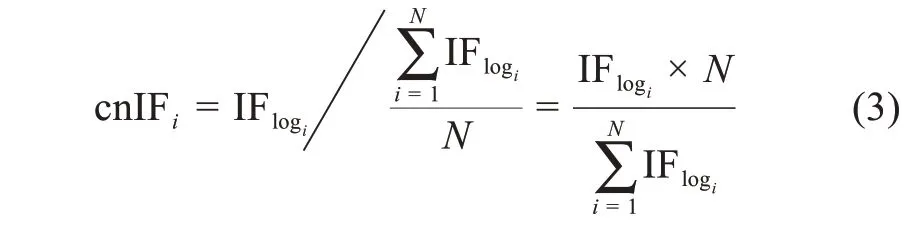
其中，N表示某学科期刊总数；IFlogi表示该学科第i种期刊的对数矫正影响因子，其由公式(4)求得。

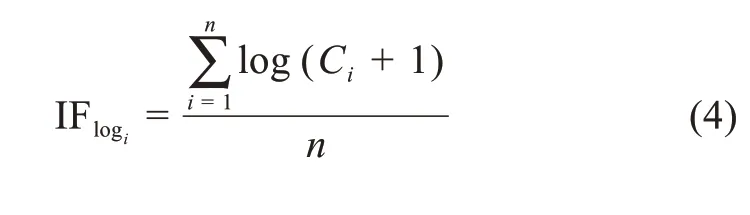
其中，Ci表示某期刊第i篇文献在统计年的被引频次；n表示该期刊前2 年发表的研究论文和综述的数量。根据对数的底数的不同，对数矫正影响因子分别表示为IFlog1.5、IFln、IFlog5和IFlog10。

4 实证研究

4.1 研究对象

本研究的目的之一是矫正期刊影响因子的学科差异，使矫正后的影响因子能够较为合理地应用于不同学科期刊的评价。如果想要实现不同学科期刊之间的比较，研究对象必须包括多个学科。因此，本研究选择了5 个学科期刊以及其在2016—2017 年发表的可被引文献（研究论文和综述）作为研究对象。学科的选择主要考虑三个方面：①自然科学领域；②学科规模不宜太小，适宜进行统计学处理。确定的入选条件为：期刊数量＞30，可被引文献量＞5000；③尽可能包括快移动学科（老化速度较快）和慢移动学科（老化速度较慢）[35]，主要体现在学科集合被引半衰期的差异方面。本研究最终选择的5 个学科为：Engineering, Environmental （环境工程）、Geology（地球科学）、Materials Science, Bio‐materials（生物材料）、Ophthalmology（眼科学）和Virology（病毒学），包括225 种期刊。各学科的基本情况如表1 所示。

表1 研究对象所属5个学科及其基本情况

4.2 研究方法

4.2.1 数据获取

登录Web of Science（WoS）数据库，选定WoS核心合集中的SCI-Expanded 作为数据来源。以JCR中5 个学科期刊的ISSN 号编制高级检索式进行文献检索，文献发表的时间窗口确定为2016—2017 年，如环境工程学科检索式为：IS=(0926-3373 OR 1385-8947……OR 0921-3449) AND PY=2016-2017。通过数据库“精炼”功能，仅保留可被引文献，即Arti‐cle（研究论文）和Review（综述）。通过“创建引文报告”，导出所有论文各年度被引频次，保留每篇论文2018 年被引频次（C2018）用于影响因子等指标的计算。

4.2.2 论文被引频次分布的正态转换和cnIF的计算

本研究采用取对数的方法对论文被引频次分布进行正态转换，通过转换需要达到两个目的：①被引频次取对数后，数据呈现较好的正态分布，这样的数据取平均值才具有统计学上的合理性；②尽可能保证转换后的数据足够大，使被引频次取对数后计算的各期刊影响因子具有一定的区分度。由于对数的底数大小直接决定了转换后数据的大小，因此，本研究采用不同底数（1.5、e、5、10）的对数转换，观察其效果。另外，许多论文被引频次为0，而0 没有对数，故本文在取对数前对所有论文的被引频次均加1。

取对数方法用公式表示为：log1.5(Ct+1)、ln(Ct+1)、log5(Ct+1)、log10(Ct+1)和log1.5(C2018+1)等。Ct为某期刊2016—2017 年的论文发表后累计到2018 年的被引频次，为计算累积影响因子[36]的被引频次。C2018为某期刊2016—2017 年的论文在2018 年的被引频次，为计算各期刊2018 年影响因子的被引频次。

根据公式(4)计算每个学科各期刊的IFlog，然后将IFlog代入公式(3)计算各期刊cnIF。

4.2.3 对比指标的选择

1）IF2018

IF2018是根据各期刊2016—2017 年发表的Article和Review（可被引文献）在2018 年的篇均被引频次计算而来，与JCR 中各期刊2018 年的影响因子高度一致（r=0.996，P=0.000）。故本研究统计分析均使用IF2018代替2018 年版JCR 期刊影响因子。

2）平均影响因子百分位

影响因子百分位是2015 年升级版InCite JCR 中推出的一个新的期刊评价指标[30]。该指标是将期刊影响因子排名转化为百分位数值，从而实现不同学科期刊的跨学科评价[21,37]。平均影响因子百分位（average JIFP，aJIFP）为该期刊在JCR 中所属学科JIFP 的平均值，来源于2018 年版JCR。

3）期刊PR8 指数

期刊PR8 指数（journal index of eight percentile rank classes，JIPR8）是指一定时间窗口内某期刊发表的可被引文献被引频次的PR8 赋值总分与该时间窗口内可被引文献数量的比值。PR8 赋值方法如下：将某期刊2016—2017 年论文按照其在2018 年的被引频次百分位升序排列，分为8 个百分位数区段， 即(0， 0.01%]、 (0.01%， 0.10%]、 (0.1%，1.0%]、 (1.0%， 5.0%]、 (5.0%， 10.0%]、 (10.0%，25.0%]、(25.0%，50.0%]、(50.0%，100.0%]，分别赋值100、80、60、50、40、30、20、10（所有零被引论文赋值0 分）。

4）rIF2018

rIF2018为某期刊IF2018除以该期刊所属学科所有期刊IF2018的平均值，是对期刊影响因子最简单的学科标准化处理。

4.2.4 统计学方法

本文采用SPSS 18 进行数据统计分析。采用QQ 图观察期刊论文被引频次正态性转换效果，期刊影响因子分布的正态性检验采用Kolmogorov-Smirnov 检验，正态分布和非正态分布数据的相关性检验分别采用Pearson 和Spearman 相关分析，各指标在不同分区期刊之间的差异分析采用Kruakal-Wallis 检验。检验水准为α=0.05。

表2 JCR中Virology学科各期刊IF2018及对数矫正影响因子

4.3 结果与分析

4.3.1 同一学科期刊对数矫正影响因子及其与传统影响因子的比较

以Virology（病毒学）学科为例，本研究计算了各期刊不同底数（1.5、e、5、10）的对数矫正影响因子，包括IFln、IFlog1.5、IFlog5和IFlog10，如表2所示。对表2 中各指标统计分析发现，该学科期刊IF2018和rIF2018不呈正态分布，不同底数的对数矫正影响因子均呈正态分布。不同底数的对数矫正影响因子之间100%相关（Pearson 相关分析，r=1.000，P=0.000），不同底数对数矫正影响因子与IF2018均有极高相关度（Spearman 相关分析，均为r=0.994，P=0.000）。对数矫正影响因子具有如下特点：①矫正后的影响因子值明显小于影响因子，且对数的底数越大矫正影响因子越小；②从期刊排序来讲，不同底数的对数矫正影响因子值有明显差异，但期刊排序完全相同（Virology 学科没有例外）；③尽管各期刊对数矫正影响因子与传统影响因子位次相差不大，但超过半数期刊（19/36）的位次发生了变化。为了使矫正后的影响因子值不至于过小，以保持其对期刊评价的区分度，本研究选择以1.5 为底数对被引频次取对数进行影响因子矫正。

选定的5 个学科中，各学科期刊IFlog1.5均呈正态分布，Kolmogorov-Smirnov 检验结果如下：病毒学，Z=0.583，P=0.886；地球科学，Z=1.178，P=0.124；环境工程，Z=0.726，P=0.668；生物材料，Z=0.389，P=0.998；眼科学，Z=0.797，P=0.549。

4.3.2 对数矫正影响因子与传统影响因子的学科差异性

不同学科之间期刊影响因子不具有可比性，主要是因为不同学科期刊影响因子存在较大差异。因此，本研究认为，哪个指标在不同学科期刊中变异程度越小，说明该指标学科差异越小，跨学科期刊评价效果相对也越好。为了比较各指标的学科差异程度，本研究计算了IF2018等9 个指标的变异系数（表3）。显然，IF2018学科差异最大，其次是经过学科标准化处理的rIF2018，学科差异最小的是经过对数矫正后再进行学科标准化处理的cnIFlog1.5。aJIFP和JIPR8 的跨学科评价效果已经得到确认[21]。

表3 5个学科225种期刊各指标的变异程度

4.3.3 5 个学科期刊对数矫正影响因子与其他文献计量学指标的关系

Kolmogorov-Smirnov 检验结果显示，5 个学科225 种期刊IF2018和rIF2018不呈正态分布，aJIFP、JIPR8、IFlog1.5、IFln、IFlog5、IFlog10和cnIFlog1.5均 呈 正态分布。因此，IF2018和rIF2018与其他指标的相关检验采用Spearman 相关分析，aJIFP、JIPR8、IFlog1.5、IFln、IFlog5、IFlog10和cnIFlog1.5之间相关检验采用Pear‐son 相关分析，具体结果如表4 所示。相关分析结果表现出以下特点：①任意2 个指标均呈高度相关（相关系数r＞0.800）；②IFlog1.5、IFln、IFlog5和IFlog10等4 个对数矫正影响因子中任意2 个指标相关系数均为1.000（100%相关）；③与2 个已确认的跨学科期刊评价指标aJIFP 和JIPR8 相关系数最大的是cnIFlog1.5和rIF2018。

表4 对数矫正影响因子与其他文献计量学指标的相关性

4.3.4 不同分区期刊各指标的组间差异和组内变异程度

以期刊JCR 分区为依据，将225 种期刊分为Q1、Q2、Q3 和Q4 等4 组，各指标组间差异检验统计量见表5，组内变异情况见表6。期刊分区的目的是实现简单的跨学科评价，4 个分区之间差异性越大，说明指标的区分度越好。就跨学科期刊评价来讲，各指标4 组期刊之间差异越大，其跨学科评价效果相对越好；而对于同一分区的期刊，就相当于同一级别的期刊，指标的差异越小越好。因此，理想的跨学科期刊评价指标应该是：Q1、Q2、Q3和Q4 等4 个组间差异非常明显（区分度非常好），而同一组（分区）内指标的变异程度较小（一致度非常好）。表5 显示，各期刊评价指标组间差异检验统计量保留3 位小数时P值均为零，这说明各指标差异组间差异均有统计学意义。从χ2值可以看出，aJIFP、rIF2018、cnIFlog1.5和JIPR8 组间差异最明显（这4 个指标均是经过学科标准化处理的），其他指标组间差异相对不明显。aJIFP、rIF2018组间差异之所以最为明显，可能是因为分组的依据是JCR期刊分区，三者同宗同源，均是基于期刊影响因子转换而来的，导致aJIFP、rIF2018表现出了理想的组间差异性。如果排除这一因素，表现最好的指标应为cnIFlog1.5。

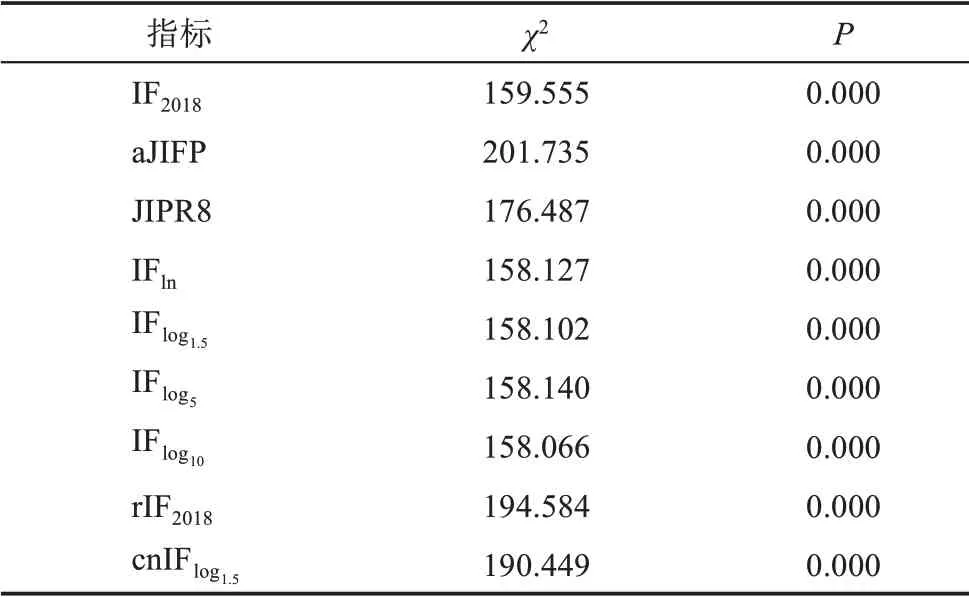
表5 各指标组间Kruakal-Wallis 检验统计量

表6 给出了每个分区期刊中各指标的变异程度。可以看出，仅在Q1 区期刊aJIFP 变异程度最小（cnIFlog1.5次之），其他3 个分区期刊中均为cnIFlog1.5变异程度最小。IF2018在Q1、Q2 和Q3 区期刊中变异程度均是最大，在Q4 区期刊排在第二。从不同分区期刊间指标的区分度和同一分区内指标的稳定性来看，cnIFlog1.5的表现也是最理想的。

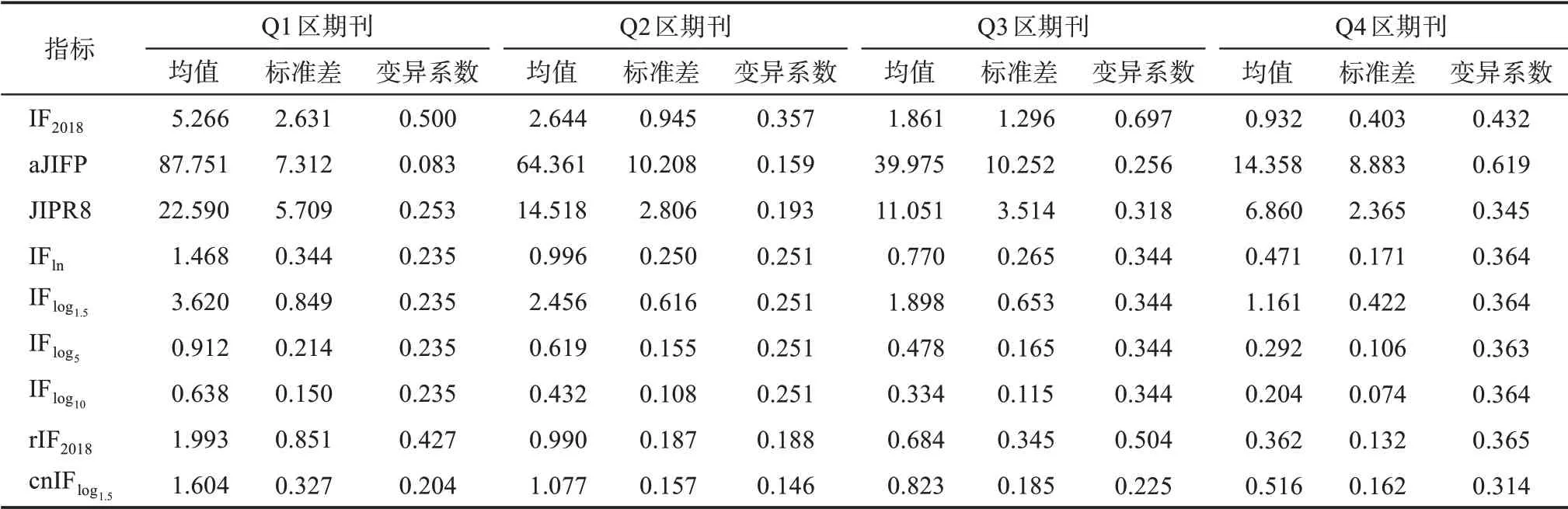
表6 4个分区期刊各指标组内变异程度

表7 不同指标排序5个学科入选Top 50期刊比较

4.3.5 不同指标排序5个学科入选Top50期刊情况

期刊评价指标学科标准化的目的是尽可能平抑指标的学科差异，使其能够较合理地应用于期刊的跨学科评价。理想的跨学科评价指标，应该是使各学科期刊有大致均等的机会入选“优秀期刊”。为了验证本研究建立的学科标准化影响因子的跨学科评价效果，首先计算按照IF2018、IFlog1.5、cnIFlog1.5和rIF2018等4 个指标排序，5 个学科入选Top50 期刊的百分比（表7）。由表7 可知，按照IF2018排序，环境科学52 种期刊入选Top 50 者达19 种（36.5%），生物材料和病毒学进入Top 50 期刊占各自学科期刊总数都超过了30.0%，而46 种地球科学期刊和59 种眼科学期刊分别仅有2 种（4.3%）和7 种（11.9%）进入Top 50，各学科入选“优秀期刊”的概率异常悬殊。IFlog1.5和IF2018相差不大，各学科入选Top 50 期刊概率最均衡的指标是cnIFlog1.5，入选概率最高的学科是环境科学（25.0%），最低的学科是病毒学（19.4%），入选Top 50 概率的最高值和最低值仅相差5.6%。

4.4 结论和讨论

4.4.1 期刊论文被引频次经对数转换后呈正态分布

几乎每种期刊论文的被引频次均为偏态分布（图1a），被引频次的偏态分布往往导致某期刊单篇异常高被引论文对期刊影响因子的畸形拉升。例如，Cancer Journal for Clinicians2012 年的影响因子达到153.459，被引频次最高的2 篇文献对其影响因子的贡献达到了70.9%[38]，这就是学术界常常诟病的影响因子的统计学缺陷。因此，若采用论文篇均被引频次构建合理的期刊影响力评价指标，必须对被引频次进行正态化转换。本研究以Geology杂志为例，验证了对数转换的有效性，而且从对图1b～图1f 的观察可知，不同底数的对数转换效果几乎没有明显区别。

众所周知，对数的底数越大，被引频次转换后的值越小，计算的IFlog也就越小。为了使各期刊IFlog具有较好的区分度，建议在保证正态转换效果的基础上，尽量使用底数较小的对数进行被引频次转换。

4.4.2 各学科期刊对数矫正影响因子呈正态分布

一般情况下，各学科期刊影响因子和总被引频次多呈偏态分布[22,34]，本研究选定的5 个学科IF2018同样呈偏态分布，且rIF2018也呈偏态分布，但是各学科期刊IFlog1.5、IFln、IFlog5、IFlog10和cnIFlog1.5均呈正态分布。由于各学科期刊影响因子大多不呈现正态分布，因此，采用各期刊影响因子除以学科平均影响因子或中位影响因子进行学科标准化都是不合理的。研究发现，几乎每个学科期刊IFlog1.5、IFln、IFlog5、IFlog10均呈正态分布，因此，本研究采用某期刊IFlog1.5除以该刊所在学科所有期刊IFlog1.5的平均值进行学科标准化处理就具有了合理性，且每个学科期刊cnIFlog1.5呈正态分布。

4.4.3 不同底数IFlog在期刊评价中是等效的

研究结果显示，无论同一学科还是不同学科期刊之间，IFlog1.5、IFln、IFlog5、IFlog10等4 个指标两两之间均呈100%相关，也就是说，这4 个指标在同一学科期刊评价或者不同学科期刊评价中是等效的。因此，本研究仅对IFlog1.5进行了学科标准化处理。

4.4.4 cnIFlog1.5是极其理想的跨学科期刊评价指标

从统计学合理性出发，本研究提出了将呈现偏态分布的论文被引频次进行对数转换后计算IFlog，对影响因子的统计学缺陷进行了矫正。在此基础上，本研究采用除以学科平均值的方法对IFlog进行学科标准化处理，创建了cnIFlog1.5，使得指标设计更加科学合理，而且其跨学科期刊评价效果得到了实证研究的充分支持：①在观察的9 个指标中，cnIFlog1.5的学科差异程度是最小的（变异系数仅0.453）；②与两个已确认的跨学科评价指标aJIFP 和JIPR8 高度相关；③以JCR 期刊分区进行分组，cnIFlog1.5具有理想的组间区分度（即Q1、Q2、Q3 和Q4 期刊cnIFlog1.5差异明显） 和优异的组内稳定性（即同一分区期刊指标的差异程度最小）；④以cnIFlog1.5为评价指标对5 个学科期刊排序，各学科期刊进入Top 50 的几率差异程度最小。

本研究首先对影响因子进行统计学缺陷矫正，然后对经过统计学矫正的影响因子进行学科标准化处理，创建了cnIF。通过理论分析和实证研究证实，cnIFlog1.5在学术期刊的跨学科评价方面具有极大的优越性，值得推广应用。