一类具有时滞的非线性物价模型的稳定性与Hopf分支

廖茂新,邓兴颖,张露露

(南华大学 数理学院,中国 衡阳 421001)

0 引 言

在市场经济中，商品的供给、需求都与物价存在着一定关系。本文假设需求与价格的关系，不是线性的，当价格不超过购买力所能承受的最大值时，需求刺激物价上涨，物价与需求正相关，而当物价上涨超过这个值时，随价格的上升，购买量会下降，两者负相关。供给与价格的关系则是正相关的，但是价格对供给量的影响，不应该是简单的随着价格的上升供给无限制的上升，因此本文假设供给函数是价格的分式线性函数，并且存在时间的滞后。

1 模型的建立

为更准确的反映物价变化的过程，王树禾在《微分方程模型与混沌》(见文献[1])一书中探讨与线性方程相比其更能反映物价变化的一些深层次规律，通过设p(t)，Q(t)，S(t)，D(t)分别表示t时刻的价格、库存、供给与需求，建立了如下关于物价的非线性微分方程模型：

(1)

(2)

S(t)=S0+α

(3)

(4)

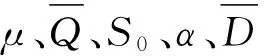
(5)

考虑到价格对供给量的影响，不应该是简单的随着价格的上升供给无限制的上升，并且其中存在时滞，因此这里将供给函数(3)改成如下形式：

(6)

其中，τ>0是反应时滞，则得到了关于物价的非线性微分方程模型：

(7)

下面将对模型(7)的动力学行为进行研究，利用泛函微分方程的稳定性理论与Hopf分支理论讨论了模型(7)的稳定性与Hopf分支的存在性。

2 模型的动力学分析

2.1 平衡点的稳定性

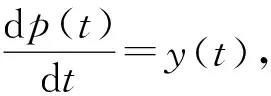
(8)

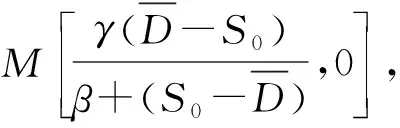
(9)

系统(9)的特征方程为：

经过计算可得到方程：

(10)

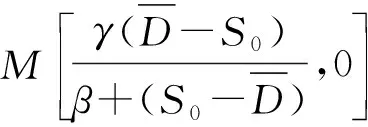
证明：当τ=0时，方程(10)变为：

(11)

特征根为：

当且仅当ap02+bp0+c<0时，方程(11)的所有根具有严格负实部。

2.2 模型Hopf分支的存在

下面将研究时滞τ对系统(8)动力学行为影响。即对系统(8)的平衡点M的稳定性和周期解存在性的影响。

引理2特征方程(10)有唯一一对纯虚根±iω0。

证明：设iω(ω>0)是方程(10)的根。代入(10)并进行实虚分离得：

(12)

两边平方相加得：

(13)

可得：

(14)

显然，方程(14)仅有一个正实根

(15)

将ω0代入式(12)计算得

其中j=0,1,2

(16)

为了证明系统(8)Hopf分支的存在，下面证明横截性条件。将方程(10)对τ求导数得

整理得

于是有

当τ=τ0时

所以有

由引理1、2结合Hopf分支理论与文献[5]可得到如下结论：

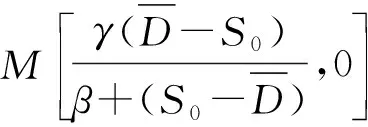
3 数值模拟

由定理1可知，当选择τ=11<τ0=12.3267时，对应的波形和相位图如图1所示。当τ=13>τ0时,对应的波形和相位图如图2所示。

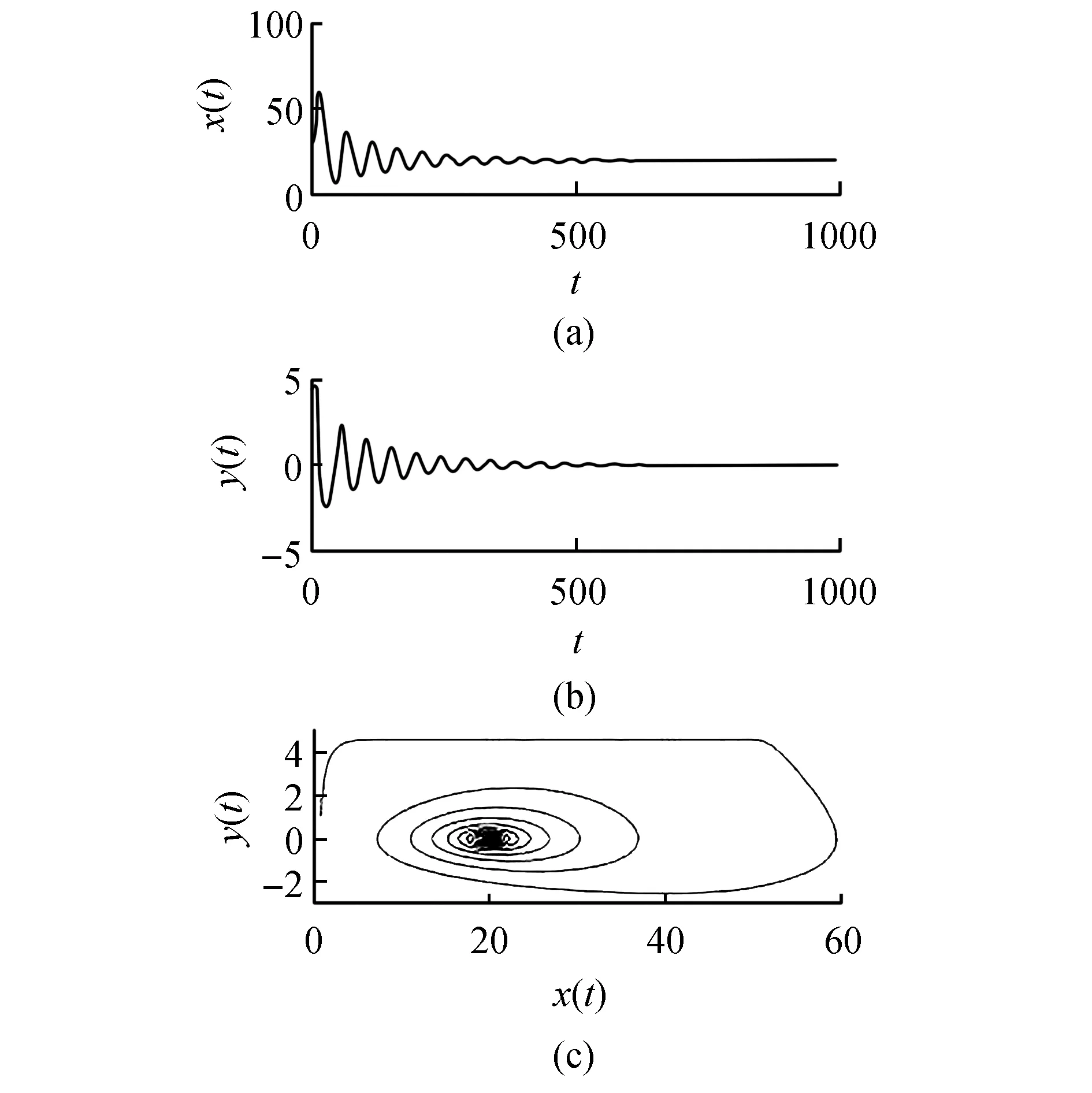
图1 当τ=11<τ0时，系统(8)的零解是稳定的Fig.1 when τ=11<τ0 , the zero solution of system (8) is stable

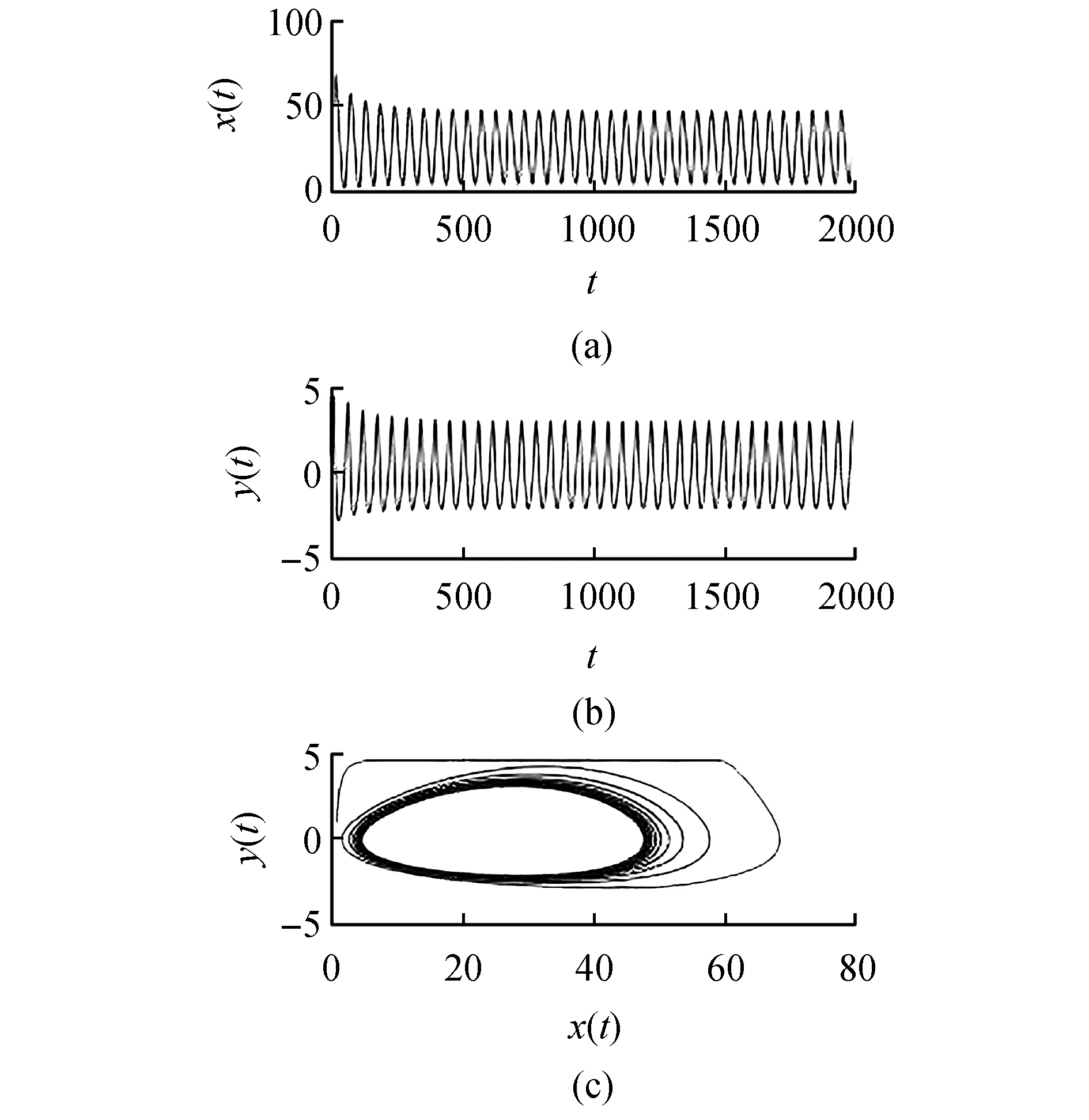
图2 当τ=13>τ0时，系统(8)在平衡点处丧失稳定性、出现Hopf分支Fig.2 When τ=13>τ0, the system (8) loses stability at the equilibrium point, and the Hopf branch appears

由图1可以看出，平衡点是稳定的。由图2可知，系统(8)在平衡点经历Hopf分支。并且时滞对系统(8)的动力学行为有显著影响。