具有非对称条件下二阶非自治系统同宿解的多重性
2021-03-15陈会文李家萌
肖 可,陈会文,李家萌
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言
考虑二阶非自治系统
(1)
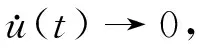
当B=0时,系统(1)为二阶Hamilton系统,
ü(t)-L(t)u(t)+W(t,u(t))=0,∀t∈R
(2)
很多文章在对L和W进行的各种假设条件下,运用了变分方法研究系统(2)哈密顿系统同宿解的存在性和多重性,如文献[2-6]。Hamilton系统作为动力系统的一种特殊情况,在物理和数学的研究领域,是当前十分热门的问题之一。它在相对论力学、气体动力学、核物理、数理科学、生命科学等各个方向都扮演着重要角色。Hamilton系统同宿解作为Hamilton系统的主要研究内容,并且知道Hamilton系统是具有变分结构的,所以可以把求系统的解转化为探求与之相对应的泛函的临界点。近年来,越来越多的学者开始利用变分法来研究Hamilton系统的同宿解、异宿解,但很多的文章结论都是在对称条件下得到的,如文献[2-8],而非对称条件的文章较少,如文献[9-10]。
与B=0的情况相比,B≠0的情况更加复杂且更加一般,对于B≠0的研究如文献[3,8,10-14],但这些都是在对称条件下得到的,很少有人在非对称的基本条件下,研究同宿解的多重性。根据这样的背景下,本文在设定了非对称的条件后,并且考虑了B≠0的情况,研究系统(1)同宿解的多重性。
假设条件:
(S0)W(t,u)=λa(t)G(u)+μb(t)F(u)。
(S1)L∈C(R,RN×N),L(t)是对称正定矩阵,t∈R,且存在函数α:R→R使得α(t)→+∞,|t|→∞,以及(L(t)u,u)≥α(t)|u|2。
(S2)G,F∈C1(RN,R),G(0)=F(0)=0。
(S3)b∈L∞(R,R),并且对一些γ∈(0,1)。a∈L∞(R,R)∩L2/(1-γ)(R,R),b是一个正连续函数。
(S6)存在ζ∈RN,使得G(ζ)>0。
(S7)存在T>0和α>1,使得|F(u)|≤T(|u|+|u|α),∀u∈RN。
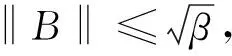
定理1假设(S0)~(S8)成立,那么就会存在λ1>0,使得对每一个λ>λ1,都存在有σ>0,使得对每一个μ∈[0,σ],系统(1)至少存在两个非平凡的同宿解。
1 预备知识

且对u,v∈E,设
相应范数为
引理1在E中,范数‖·‖与范数‖·‖T等价
证明:对任意的u∈E,
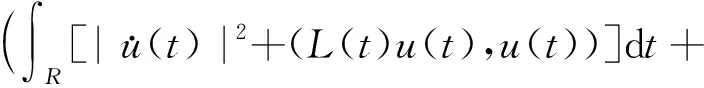

由(S8),可以有:
可以得到
运用‖u‖T作为需使用的范数。
E是Hilbert空间,E*表示E的对偶空间,因为E是连续嵌入LP(R,RN)。∀P∈[2,+∞),所以存在δp>0,使得
‖u‖P≤δp‖u‖T,∀u∈E。
(3)
其中‖u‖P表示LP(R,RN)的范数。
引理2(参考文献[15])假设L满足条件(S1),则对任意的2≤P≤∞,E是紧嵌入LP(R,RN)。
对任意的u∈E,定义
(4)
引理3假设(S0)~(S8)成立,定义泛函
(5)
那么I是有意义的,并且I∈C1(E,R),它的导数是
(6)

证明:该引理的证明过程与文献[10]中引理2.3的证明过程类似,故该引理的证明过程省略。
引理4Φ是强制的泛涵,弱下半连续的,在E的每个有界子集上有界,并且它的导数存在一个连续逆。
证明:首先容易得到Φ是强制的。设在E中uk→u,那么
所以有
接下来证明Φ′存在一个连续逆,对每一个u∈E{0},由式(6),可以有
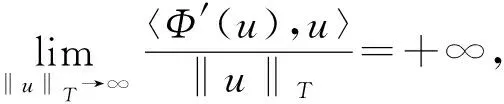
〈Φ′(u)-Φ′(v),u-v〉=‖u-v‖2
所以Φ′是一致单调的,由文献[16]中的Theorem 26,可以得到Φ′存在一个连续逆E*。
2 定理1的证明
在证明定理1的过程中运用了参考文献[17]的Theorem 1。

证明:由(S2),(S4)和(S5),则对任意的ε>0,存在Tε>0,使得
(7)
由此,可以得到
大白兔“诞生”于1959年,美加净“诞生”于1962年,在那个年代,大白兔奶糖和美加净护肤品风靡一时,受到消费者的喜爱。大白兔成为建国十周年的献礼产品,产品经销全世界40多个国家和地区,成为国际市场上经久不衰的大众宠儿。美加净创造了很多中国化妆历史上的“第一”,第一支护发定型摩丝、第一款护手产品——美加净护手霜,上海家化还推出了美加净青苹果香波,这是国内首个“二合一”(洗发+护发)香波洗发水。


证明:
由(S4)和(S5),则对任意的ζ<0,存在ηζ∈(0,1)使得
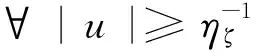
(8)
又因为G∈C1(RN,R),存在一个常数Cζ>0,使得
(9)
这里的γ由(S3)中给出,可以得到
所以

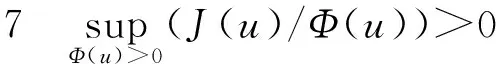

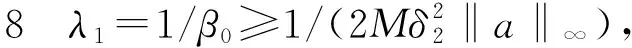
证明:由(S3),可得
证明完毕。
综上所述,E是自反的,可分的,一致凸的Banach空间。由引理2~引理8,得到Φ,J,Ψ满足文献[14]中的Theorem1所有条件。所以,对每一个λ>λ1,存在σ>0,使得对每一个μ∈[0,σ],I在E中至少存在三个临界点。并且0是系统(1)的解。所以,系统(1)至少存在着两个非平凡的同宿解。
