可搭载切割设备的移动式升降平台关键部件可靠性分析

2021-03-15邹树梁陈树强黄斌海

南华大学学报（自然科学版） 2021年1期

邹树梁,陈树强*,黄斌海

(1.南华大学资源环境与安全工程学院,湖南衡阳 421001,2.核设施应急安全技术与装备湖南省重点实验室,湖南衡阳 421001)

0 引言

在我国某核工程设施退役过程中有大量试剂输送管道、蒸汽管线、压空管道等需要拆除，这些管道一般距离地面有1～6 m的高度，使得拆除工作有一定的难度。目前普遍采用的拆除方法是冷切与热切相结合的办法，即人员在搭设好的脚手架上利用剪切设备如液压剪切机、往复锯等冷切方式或者采用离子电弧切割等热切割方式对管道进行拆解。由于管道高度不一致，每次剪切时脚手架需搭接的高度也不一致，使得工作量增加。并且人员站在脚手架上工作，危险系数相对较高[1-2]。为提高工作效率，降低危险，在现有移动式升降机基础上，设计出一种全自动多自由度移动式升降平台[3]的基础平台，搭载拆除设备实施管道拆除工作。由于移动式升降平台工作环境复杂，零部件易受到辐射，容易加速其失效，如在作业中途失效便会造成巨大损失。因此，通常需对设备进行可靠性分析，提高其安全性并减少经济损失。

针对可靠性[4]的研究，V.Talbofer和S.Hoskova[5]运用统计学及模糊概率理论，通过对数据和空间信息的精确捕捉完成对指挥控制系统的可靠性分析评价。赵德孜[6-7]则是提出模糊综合评价的改进方法，以航空发电机为对象，对系统初期进行可靠性分配。邹小琦[8]以滚珠丝杠副为研究对象，分析工作中实际负载和工作寿命分布状态，阐述了滚珠丝杠副的可靠性设计方法。刘英[9]等通过对数控刀架系统建立模糊故障树，发展三角函数用以确定部件失效概率，从而对数控刀架系统进行可靠性分析。在模糊状态理论中，一般采取专家打分法获取可靠性数据，但专家打分主观性较大，难以精确估算事件概率。在1992年S.J.Chen[10]等提出左右模糊排序法，提出了模糊数向模糊概率的转换。左右模糊排序法利用的是左右优势度及贴合度来定义正负理想点，并通过α截集将模糊数变为区间数，再将期望值映射到数轴上，利用其距离形成一个类似贴近度的综合排序指标，该方法在后面获取可靠性数据方面应用比较广泛，如张静[11]等利用左右模糊排序法计算了汽油管道的泄露概率；T.Onisawa[12]研究了人机系统中人的失误概率也是应用的左右模糊排序。

1 移动式升降平台可靠性分析模型

可搭载切割设备移动式升降平台[13]工作环境复杂，在作业中出现故障将会造成较大的损失，由于设备工作环境的特殊性，相同部件故障率也将会有所差异，因此，本文将采用模糊集理论来确定各部件的失效概率。沿用专家评判的方法，通过改进的隶属度函数将专家评判转换为模糊数，最后采用左右模糊排序法转换模糊数为失效概率。

1.1 建立专家评语集

在评价具体事物时，将评价的结果分成具体的等级。通常用集合P={p1,p2,…,pn}表示。本文为评价可搭载切割设备移动式升降平台关键零部件的失效概率，可建立评语集：P={很小，小，较小，中，较大，大，很大}。组织相关专业的专家小组，对相关部件依次用评语集进行评价。

1.2 专家意见量化

在专家对关键部件进行评判后，利用模糊集处理专家的评判意见。本文采用岭行隶属度函数[14]将专家意见量化，其相较三角及梯形隶属度函数具有更好的平滑性。而一般中间型隶属度函数通常用于一级评语，为了改善平滑性并适用多级评语，将采用改进的中间型岭型隶属度函数[15]，见式(2)。

偏小型隶属度函数为

(1)

改进的中间型隶属度函数为

(2)

偏大型隶属度函数为

(3)

式中n为评语的总集数；ni为级数，例如评语集为{很小，小，较小，中，较大，大，很大}，n=7，令ni=i，当评语为“很小”时，i=2，当评语为“小”时，i=3。

1.3 计算模糊数

对应评语集建立隶属度函数，对专家评判意见进行模糊数计算，采用模糊集的∂截集。设式(1)～式(3)的∂截集为∂=[k1,k2]，k1和k2为∂截集的上限和下限。式(1)～式(3)的截集计算如下。

1)偏小型隶属度函数截集为∂=[s1,s2]。

则

2)中间型隶属度函数的截集为∂=[z1,z2]。

则

3)偏大型隶属度函数截集为∂=[l1,l2]。

则

通过计算上述截集，得到的模糊集可适用于多级评语。也得到了各种模糊语言与模糊数w对应的关系函数。

偏小型为

(4)

中间型为

(5)

偏大型为

(6)

1.4 模糊数转换为模糊率

通过计算模糊数w，转换专家意见为[0,1]的模糊集合，采用左右模糊排序法将模糊数转换成模糊分数s。

则左、右模糊可能性值可表示为

(7)

(8)

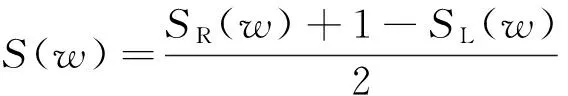
(9)

将模糊可能性分数S转换为模糊失效概率P。

(10)

(11)

由此，结合模糊数学与专家打分建立移动式升降平台失效概率的计算模型。改模型的操作步骤见图1。

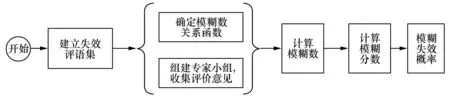
图1 移动式升降平台可靠性计算流程Fig.1 Flow for reliability calculation of mobile lifting gear

2 模型的应用与分析

选取移动式升降平台传动系统的零部件为例，计算其失效概率。根据移动式升降平台在实际工作过程中，传动系统属于比较容易出故障的地方。因为其工作场地的特殊性，一旦发生故障，工作人员很难进行维修，因此，对传动系统零部件进行可靠性分析对工装的安全持续使用有着重要意义。

2.1 专家评价意见

1)权重的确定

组织专家对平台传动系统各零部件进行故障模式的评判。由于各个专家的经验、知识层面等影响因素差异，评价结果也会有差异，为了提升结果正确性，根据各自情况赋予相应专家对应权重。设专家小组为n位，每位权重为mj，则专家权重计算式为

(12)

式中Cj为第j位专家所得的分，参考表1给每位专家打分。

在此次评价中，共邀请了5位专家，其中两名教授，一名安全工程师，一名机械工程师，一名维修专家。依据表一评分标准，对5位专家的资质，工龄，学历等进行打分，然后根据分值估算权重值，见表2。

2)专家评价结果

本文选取了传动系统零部件各2中常见失效模式为算例。5位专家对每个零件的每种故障模式进行评价，其评价结果见表3。

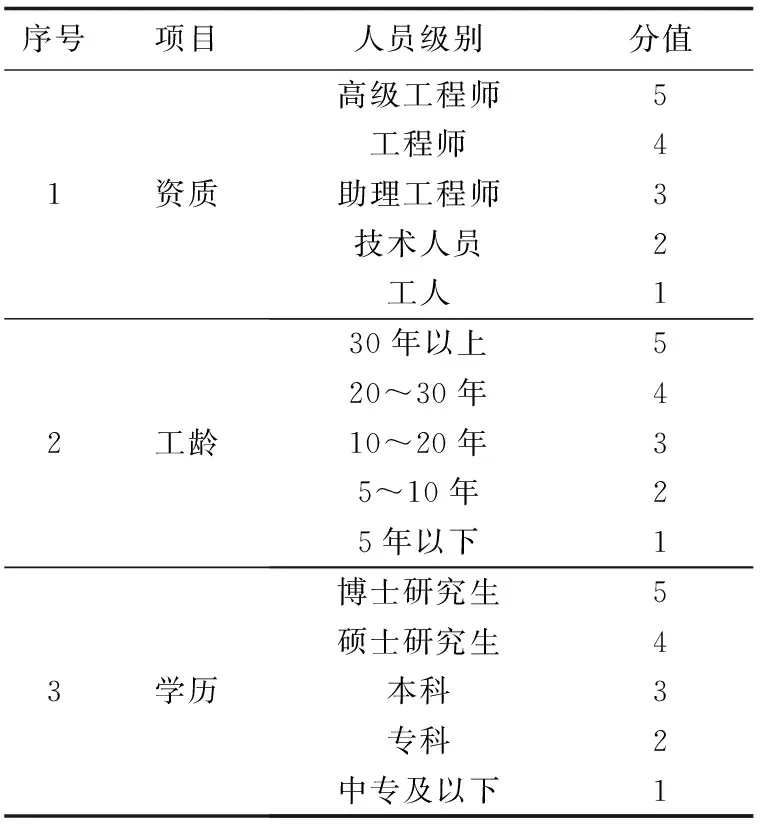
表1 评估小组成员的分值分配Table 1 Score allocation of panel members

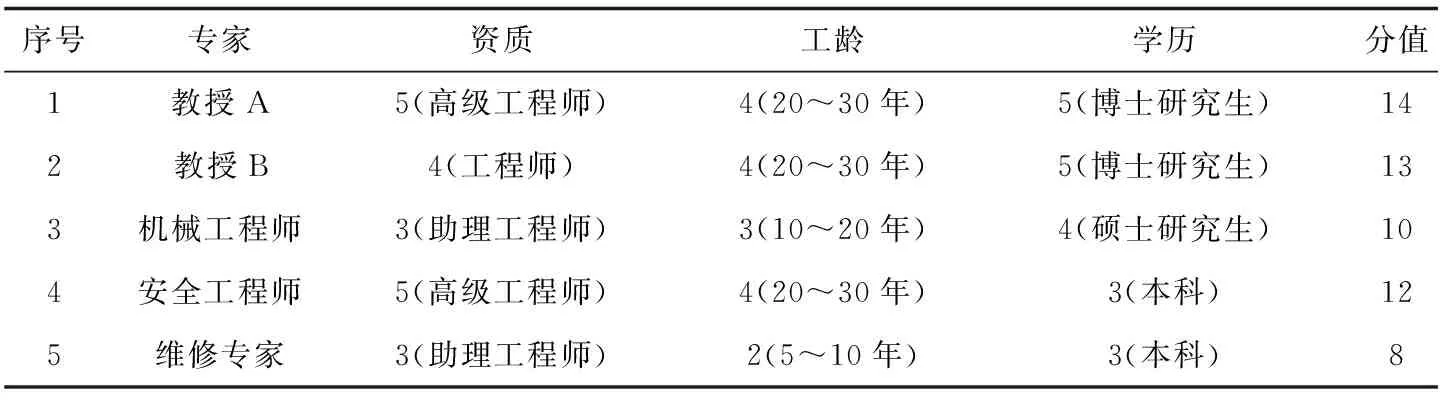
表2 专家权重分配Table 2 Expert weight allocation

2.2 失效概率的计算

由于故障评语集语言分为7个等级，为了保持隶属度函数的连续性和平滑性，取a=0.125，b=0.25，n=7，i=1，2，3，…，7。因此得出模糊数的关系函数。

(13)

(14)

(15)

当评语为“很小”时，记i=2，当评语为“小”时，记i=3，以此类推ni=i。

根据专家评价结果，“轴疲劳断裂”失效计算

因此

同理对“轴重心偏置”失效可能进行计算得

移动式升降平台传动系统关键零部件故障概率计算结果见表4。

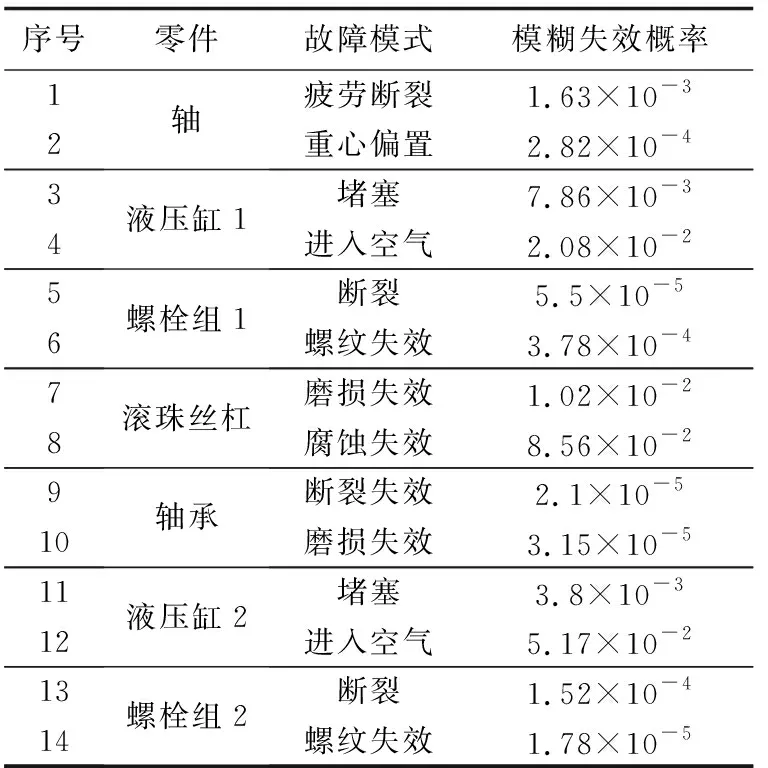
表4 传动系统零部件故障概率计算结果Table 4 Calculation results of failure probability of transmission system components

由计算结果可知，液压缸跟滚珠丝杠模糊失效概率较高，可靠性较低。计算结果与实际零部件可靠性对比，计算结果与实际较为贴近。因此，滚珠丝杠与液压缸作为系统薄弱环节，提高其安全性能，增加可靠性对移动式升降平台的安全性能与实际安全操作具有重要意义。

液压缸系统在停止瞬间，主要体现在对活塞杆的冲击上，因此，需提高活塞杆的强度，保证活塞杆承受冲击时有一定的安全余量。由于长时间的柱塞运动，频繁的摩擦，提高油液质量也至关重要，保证油液不含杂质。长期往复运动会造成柱塞杆的应力疲劳，甚至断裂失效，需定期进行探伤检测，保证柱塞杆疲劳强度。滚珠丝杠主要失效形式为表面损伤失效，断裂失效。表面损伤失效主要考虑润滑与工作环境，应优化润滑方式，选择合适的润滑剂和润滑量，安装时保证零件与环境的清洁，优化密封结构。断裂失效是由于载荷过高，异物污染以及材料缺陷造成，因此应选用合适的产品，避免冲击振动，保证工作环境的清洁，选用合适的密封产品。