延时可修系统的可靠性分析与计算
2021-03-15刘亚春曹远龙
刘亚春,曹远龙
(1.南华大学 数理学院,湖南 衡阳 421001;2.南华大学 机械工程学院,湖南 衡阳 421001)
computation
0 引 言
在研究系统的可靠性时,一般都假定系统发生故障后能够立即开始维修[1-4]。然而,在生产实际中,修理人员可能已离岗、或正在从事其他工作,致使系统发生故障后需要等待一段时间才能开始维修,这种情况称为修理延迟。目前,人们一般采取两种方式分析或计算系统的可靠性。一种方式是:先确定系统的状态变量,进行状态分析,然后运用马尔可夫过程理论,建立微分方程或状态转移方程,得出系统在任一时刻处于各状态的概率,进而计算可靠性指标[2-6];另一种方式则是利用全概率公式和分解技术,运用更新过程理论,使用积分法,直接计算系统的可靠性指标[7-9]。
系统正常工作的时间、延迟维修时间以及修理时间等随机变量的分布规律决定了系统的可靠性。修理工“休假”只不过是造成延迟维修的原因。所谓“休假”是指“修理工已离岗休息或正在从事其他工作”。所谓“单重休假”,是指修理工每次只能休假一次,若系统在修理工休假期间发生故障,那么必须等到修理工休假结束才能开始维修;如果系统在修理工休假期间没有发生故障,那么系统在下一次发生故障时便能马上得到维修,系统修复后,修理工才能开始下一次“休假”。所谓“多重休假”,是指修理工在休假结束时,如果系统是正常的,则可以再次休假。一些文献研究了“单重休假”和“多重休假”对系统可靠性的影响[3,6,8-9];显然,无论是单重休假还是多重休假,休假的时刻与系统的工作状态具有相依性;休假模式过于理想化,不切实际;此外,系统或部件的失效时间、休假时间或维修时间不一定服从文献中假定的指数分布等。特定的分布假设虽然为建模和求解提供了方便,但却局限了理论研究的应用范围。
1 可修系统的状态分析与可靠性计算
任何时候,一个可修系统只有三种状态:“正常工作”、“等待维修”或“正在维修”。记系统的正常工作时间、延迟修理时间和维修时间分别为ξ、η、ζ,其统计分布函数分别为F(t)、G(t)和H(t),概率密度分别为f(t)、g(t)和h(t),即F′(t)=f(t)、G′(t)=g(t)、H′(t)=h(t)。显然,ξ、η、ζ相互独立;假设初始时刻系统处于正常工作状态,系统在发生故障后能够被修复如新;ξk、ηk、ζk分别表示系统的第k个工作寿命、第k个延迟修理时间和第k个修理时间,显然ξk、ηk、ζk分别与ξ、η、ζ同分布(k=1,2,3,…),并构成一个更新过程。
1.1 可用度与稳态可用度的计算
设系统初始时刻为t=0;当t>0时,如果系统正常,则记S(t)=1;否则,记S(t)=0。系统的瞬时可用度A(t)=P{S(t)=1|S(0)=1},利用全概率公式,并注意到系统每次修复的时刻是再生点,得
A(t)=P{ξ1>t,S(t)=1|S(0)=1}+P{ξ1≤
t≤ξ1+η1+ζ1,S(t)=1|S(0)=1}+
P{ξ1+η1+ζ1 (1) 记拉普拉斯变换[10]: (令t-x=y) 即 [f(t)*g(t)]=f*(s)·g*(s) (2) 为运用方便,将式(2)写为 (3) 类似于式(3),递推得 (4) 在式(1)两边取拉普拉斯变换,可得 (5) 从而 A(t)=-1[A*(s)] (6) 此外 (7) 类似地,有 此外,易得 由式(5)至(12),运用洛必达法则,得稳态可用度 (13) 显然,公式(5)和(13)比文献[9]中相应的公式(1)与(2)更加简明,而又不局限于单重休假。 系统在(0,t]时间内出现故障的次数记为n(t),平均故障次数E[n(t)]记为m(t),则 E[n(t)]=E[n(t)|ξ>t]·P{ξ>t}+ E[n(t)|ξ≤t]·P{ξ≤t}=0+ E[n(t)|ξ≤t<ξ+η+ζ]· P{ξ≤t<ξ+η+ζ}+E[n(t)|· ξ+η+ζ≤t]·P{ξ+η+ζ≤t}= E[n(t-u)]]dP{ξ+η+ζ≤u}= P{ξ≤t}·P{ξ+η+ζ>t}+ ζ≤u} (14) 其中P{ξ≤t}=F(t) P{ξ+η+ζ>t}=1-P{ξ+η+ζ≤t}= f(t)*[g(t)*H(t)] (15) η+ζ≤u}=f(t)*g(t)*H(t)+ E[n(t)]*[f(t)*g(t)*H(t)]′ (16) 将式(15)和式(16)代入式(14),得 m(t)=F(t)·[1-f(t)*g(t)*H(t)]+ f(t)*g(t)*H(t)+m(t)*[f(t)* g(t)*H(t)]′=F(t)+[1-F(t)]·[f(t)*g(t)*H(t)]+m(t)* [f(t)*g(t)*H(t)]′ (17) 在式(17)两边取拉普拉斯变换,得 从而 m(t)=-1[m*(s)] (18) 稳态故障频度 本文基于系统正常工作时间、延迟维修时间以及修理时间的一般分布函数或概率密度,运用更新过程理论、全概率分解技术和拉普拉斯变换,得到了延时可维修系统的瞬时可用度和稳态可用度等的计算公式,避免了微分方程建模与求解的复杂过程。结论具有一般性,应用范围得到推广。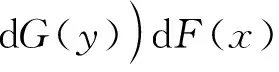
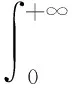
1.2 故障频度与稳态故障频度的计算
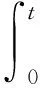
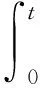
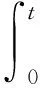
2 结论及其验证