捕食率对一类食饵-捕食者动力学模型稳定性的影响
2021-03-14王成宇申传胜陈萌昭徐王军
王成宇,申传胜,陈萌昭,徐王军
(安庆师范大学数理学院,安徽安庆246133)
生态系统是由生物群落及其生存环境共同组成的动态平衡系统,有着数以万计的物种在生态系统中不断繁衍进化。生态系统各要素之间最本质的联系是通过营养来实现的,食物链和食物网构成了物种间的营养关系,各个物种都在纵横交错的种群生态系统中进行着捕食、互惠和竞争。例如,老鹰捕食鸽子是一种捕食与被捕食关系,蜜蜂采蜜的同时也帮助花进行传粉是一种互惠关系,生活在同一块草地上的牛和羊竞争着草是一种竞争关系。但如果生态系统变得不稳定,则可能会引起地球的灾变,给人类社会带来巨大的灾难。从生态学的意义上来讲,对种群、群落、生态系统等的稳定性分析是一个重要的研究课题。对于生态系统来讲,其重要的特征之一就是稳定性,生态系统是否稳定,将直接影响生态栖息地、生物多样性等一系列环境问题。
食饵-捕食者模型自1932年提出以来就一直受到数学家、生物学家以及物理学家的推崇和研究[1]。Lotka-Volterra(LV)模型是最经典的食饵-捕食者模型,该模型假设食饵处在较为理想的自然环境中,捕食者只能依靠捕食食饵为生。但LV模型没有考虑到资源有限的情况,后来很多人对此模型进行了改进,例如引入Allee效应[2]、噪声[3]、迁移[4]、功能反应[5]等可能会造成影响的因素[6-7]。最近,我们研究了双食饵三种群模型中时变迁移对捕食者的生存与灭绝的影响[8]。此外,也有人提出两个以上物种的模型来描述类似生态现象,它们表现出非常复杂的动力学行为[9-10]。在许多文献中,一个物种往往只会被看作捕食者或食饵来进行研究[11-12]。但事实上,除非是处于食物链顶端的动物不会有被其他动物捕食的情况发生,多数动物都会出现本身既是捕食者又是食饵的情况。
本文中,我们在传统的具有被捕食与捕食关系的两个物种中引入一个新的中间物种,例如,在鹰以鼠为食的系统中,考虑蛇,显然蛇捕食鼠,蛇又被鹰捕食。我们采用Logistic人口模型和Holling-I型功能响应函数给出三个物种的动力学方程模型,得到模型平衡点的存在条件,分析平衡点的稳定性,并对非周期解进行数值模拟。
1 数学模型
考虑到自然界许多捕食行为的复杂性,我们在传统的食饵-捕食者模型中引入一个中间物种,该中间物种捕食原模型的食饵,又被原模型中的捕食者所捕食,利用Logistic人口模型和Holling-I型功能响应函数,食饵X、中间物种Y和捕食者Z及其相互作用的动力学方程模型可以表示为

其中x,y和z分别表示食饵X、中间物种Y和捕食者Z的种群密度,参数r,u,w分别是X的出生率以及Y和Z的死亡率。F1=e1αx和F2=e2βx+e3γy分别代表中间物种Y和捕食者Z的数值响应,表示Y和Z通过捕食量的变化而引起的种群数量的变化。α和β分别表示Y和Z对于食饵X的捕食率,γ是Z对于Y的捕食率。e1、e2分别表示Y和Z单位时间内消化X的转化率,表示Z单位时间内消化Y的转化率。k、ky、kz表示系统的最大环境承载能力,其中,ky=a1x,kz=,均与食饵的数量成正比。
为了使该模型的数学分析不太复杂,使用变量和参数的转换将系统(1)写成无量纲形式:

去掉“短横”得到

系统(2)的初始条件为x(0)=x0,y(0)=y0,z(0)=z0,其中,0<x0,y0,z0≤1,函数M、N1、N2在Ω3+={(x,y,z)∈ℝ3:x≥0,y≥0,z≥0}上是光滑连续函数。
定理1当t≥0时,系统(2)在Ω3+上的解存在且有界。
证明由系统(2)的第一个方程可知

即关于食饵的方程是有界的。(3)式的解为:

其中,c=( 1-x0)/x0≥0,是积分常数。因此,0<x(t)≤1,∀t>0。
接下来,证明x(t)+y(t)+z(t)≤L(三个种群密度和的最大值),∀t>0。设S(t)=x(t)+y(t)+z(t),则函数S沿着系统(2)关于t的导数为

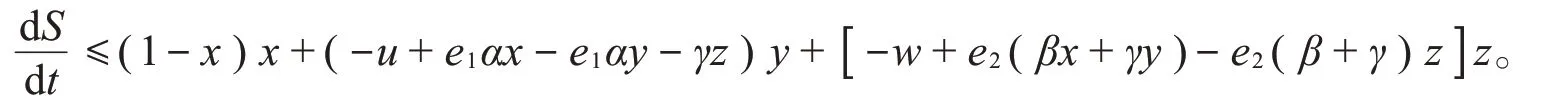
所以,

式(4)可以改写为
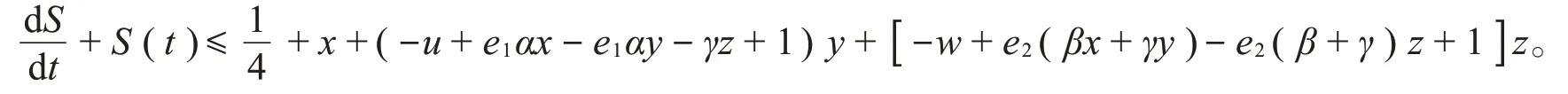
因为0<x(t)≤1,则
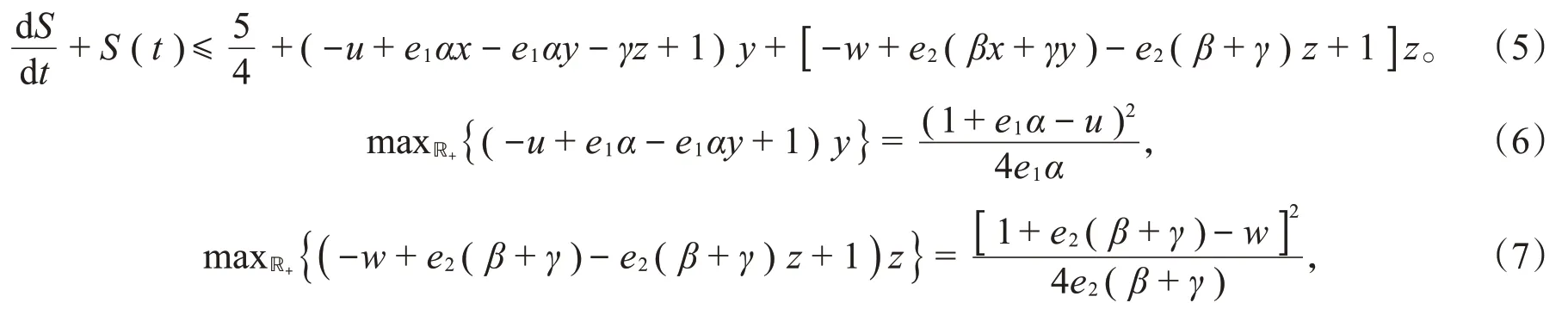
式(6)和式(7)都为正值,所以式(5)可记为:
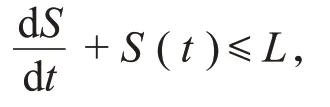
综上S(t)=x(t)+y(t)+z(t)≤L,∀t>0。
2 平衡解和稳定性分析
平衡解:系统(2)有5个非负平衡解。E0=(0,0,0)和E1=(1,0,0)显然是存在的(它们在参数上不需要满足任何条件)。然而,在坐标轴y或z上却没有平衡点,因为当食饵的种群密度x为0时,中间物种Y和捕食者Z也会随之死亡,达不到平衡状态。对于两个物种存在的情况,有两个平衡点E2和E3。平衡点受到下列方程约束:


则平衡点E2存在于xOy面的正象限内部需满足条件:


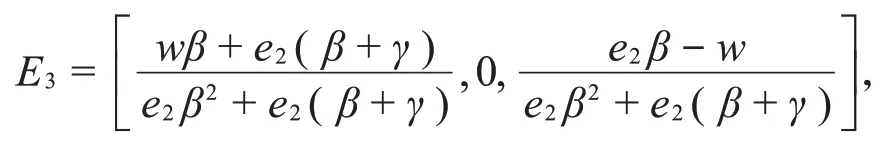
则平衡点E3存在于xOz面的正象限内部需满足:

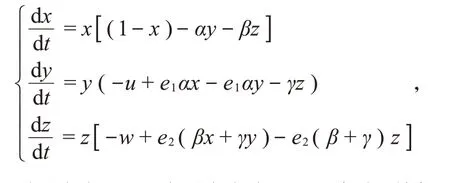
稳定性分析:为了研究上述5个平衡点的局部动力学行为,我们计算了各个平衡点的雅可比矩阵。从这些矩阵出发,利用Routh-Hurwitz判据确定各个平衡点局部渐进稳定的条件。平衡点E0=(0,0,0)的雅可比矩阵为

从矩阵J0可以看出,x方向的特征值是正的,y和z方向的特征值是负的,因而平衡点E0在x方向上是不稳定的,但在y和z方向上是稳定的。第一个平衡点E0是鞍点。
平衡点E1=(1,0,0)的雅可比矩阵为

平衡点E1若满足:

因此,中间物种Y和捕食者Z的死亡率分别大于他们总体消化吸收的效率,则E1是局部渐近稳定的。

利用Routh-Hurwitz判据,得到两个条件:

在满足条件(12)和(13)的情况下,平衡点E2是局部渐近稳定的。
又因为条件(8)是一定要满足的,所以条件(12)也一定是满足的,即平衡点E2在xOy面上一定是局部渐近稳定的。平衡点E2是否在z方向上(即与xOy面正交的方向)局部渐近稳定要取决于条件(13)是否满足。如果满足条件(13),则平衡点E2在z方向上是局部渐近稳定的。
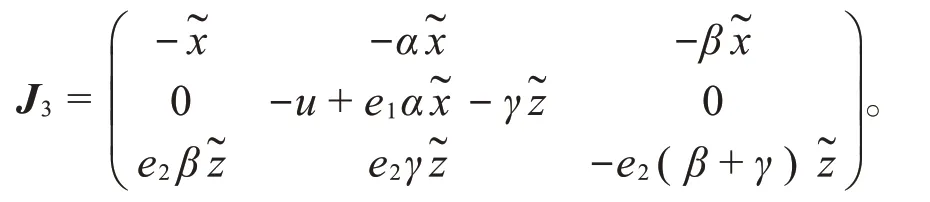
利用Routh-Hurwitz判据,得到两个条件:

在满足条件(14)和(15)的情况下,平衡点E3是局部渐近稳定的。
如若满足条件(14),那么平衡点E3在xOz面是局部渐近稳定的。又因为条件(9)是一定要满足的,所以条件(14)也一定是满足的,即平衡点E3在xOz面上一定是局部渐近稳定的;平衡点E3是否在y方向上(即与xOz面正交的方向)局部渐近稳定要取决于条件(15)是否满足。如果满足条件(15),则平衡点E3在y方向上是局部渐近稳定的。
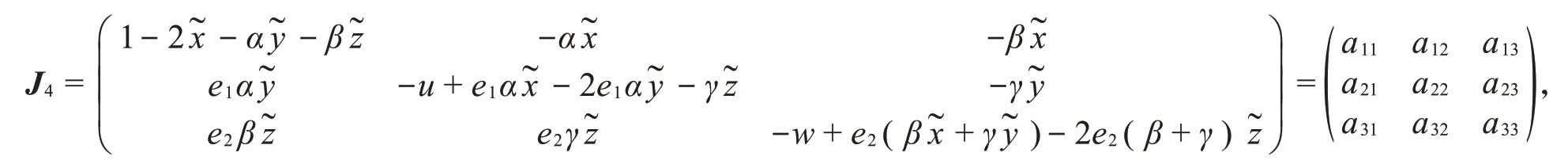
雅可比矩阵J4的特征方程为λ3+A1λ2+A2λ+A3=0。A1=-(a11+a22+a33),A2=(a11a22+a11a33+a22a33-a12a21-a13a31-a23a32),A3=(a13a31a22+a12a21a33+a11a23a32-a12a23a31-a13a21a32-a11a22a33)。
根据Routh-Hurwitz判据,平衡点E4=(~x,~y,~z)如果是局部渐近稳定的,则需要满足条件:

因此得到以下定理。
定理2(i)平衡点E0是一个鞍点,在yOz面上具有局部稳定流形,在x方向上具有局部不稳定流形。
(ii)正平衡点E1在x方向上是局部渐近稳定的,如果满足条件(10)和(11),则在yOz面上也是局部渐近稳定的。如果条件(10)和(11)有任何一个不满足,则平衡点E1为鞍点。
(iii)平衡点E2和E3为正,需分别满足条件(8)和(9)。在满足条件(12)和(13)下,E2是局部渐近稳定的,在满足条件(14)和(15)的情况下,E3是局部渐近稳定的。
(iv)非平凡正平衡点E4是存在的,在满足条件(16)(17)和(18)的情况下,它是局部渐近稳定的。
推论1如果平衡点E2的条件(13)和平衡点E3的条件(15)都不满足,那么E2和E3分别在z方向上和在y方向上是不稳定的。
定理3(i)平衡点E2在xOy面正象限内全局渐近稳定。(ii)平衡点E3在xOz面正象限内全局渐近稳定。
证明这里只证明(i),P(x,y)=1/xy是Dulac函数,它在xOy面的正象限D={(x,y)|x>0,y>0}是连续可微的。设G1(x,y)=x(1-x)-αxy,G2(x,y)=-uy+e1αxy-e1αy2,则

可以观察到,在xOy面的正象限D上∇·(PG1,PG2)不等于0且符号没有改变,根据Bendixson-Dulac准则[13],在xOy面的正象限内没有周期解,平衡点E2在xOy面正象限内全局渐近稳定。
3 数值模拟
α、β和γ代表着捕食者搜寻并捕获食饵的效率,反映了模型中主要组成部分的功能响应函数,也是模型中种内竞争系数的一部分。因此,这些参数对种群的动力学行为有着十分重要的作用。下面,分6种不同的情形来讨论捕食者Z和既是食饵又是捕食者的中间物种Y的共存与灭绝问题。我们选取的参数值分别满足平衡点E2和平衡点E3在xOy面、xOz面上的稳定性条件,满足非周期解(定理3)条件。在下文中,固定时间步长dt为0.001,三个物种密度的初始值分别为x(0)=0.6,y(0)=0.3,z(0)=0.3,参数e1=0.86,e2=0.89,u=0.57,w=0.65。图2至图7中黑色虚线、红色破折线和蓝色实线分别表示食饵X、中间物种Y和捕食者Z的密度。
第1种情况,α固定为1.12,当β值与α值接近时,这里设为1.08。图1(a)、(b)和(c)显示,只要β与α接近,不论γ增大或减小,三个物种均共存,但是它们的密度不同。当Z对Y的捕食率很低时,如γ=0.1,Y的密度大于Z的密度,如图1(a)所示;当Z对Y的捕食率中等大小时,如γ=0.8,Y的密度与Z的密度近似相等,如图1(b)所示;当Z对Y的捕食率较高时,γ=1.41,Y的密度小于Z的密度,如图1(c)所示。

图1 系统(2)在α=1.12,β=1.08时的动力学行为时间序列图。(a)γ=0.1;(b)γ=0.8;(c)γ=1.41
第2种情况,α仍然固定为1.12,当β值小于α值时,设为0.88,γ值变化。当捕食者Z对食饵X的捕食率β小于中间物种Y对X的捕食率α时,如果Z对Y的捕食率较低,γ=0.1,则中间物种Y存活而捕食者Z逐渐灭绝,如图2(a)所示。其实这也可以理解,因为Z竞争不过Y,食饵X主要被Y捕食了,而Z又很难捕食到Y。但是,如果Z对Y的捕食率提高为γ=0.8时,Z则从灭绝态转为存活态,形成三物种共存的情况,如图2(b)所示。

图2 系统(2)在α=1.12,β=0.88时的动力学行为时间序列图。(a)γ=0.1;(b)γ=0.8
第3种情况,α仍然固定为1.12,当β值大于α值时,例如为1.95,γ值变化。当捕食者Z对食饵X的捕食率β大于中间物种Y对X的捕食率α时,无论Z对Y的捕食率γ增大或者减小,Z均存活而Y灭绝,如图3(a)和(b)所示;如果Z对Y的捕食率较低,γ=0.1,则中间物种Y在t=140.6时接近灭绝,如图3(a)红色破折线所示;如果Z对Y的捕食率提高至γ=0.8时,那么,由于Z对Y的捕食率的提高而加速了Y的灭绝,Y在t=38.2时就已经灭绝了,如图3(b)所示。

图3 系统(2)在α=1.12,β=1.95时的动力学行为时间序列图。(a)γ=0.1;(b)γ=0.8
第4种情况,固定β为1.31,当α值与β值接近时,例如为1.33,γ值变化。在图4(a)、(b)和(c)中可以看出,当中间物种Y对食饵X的捕食率α接近于捕食者Z对X的捕食率β时,三个物种共存。但是,当Z对Y的捕食率为很低值时,γ=0.1,如图4(a)所示,则Y的密度大于Z的密度;当Z对Y的捕食率γ=0.55时,如图4(b)中所示,Y的密度与Z的密度近似相等;而当Z对Y的捕食率较高时,如γ=1.22,如图4(c)所示,中间物种Y的密度反而小于捕食者Z的密度。
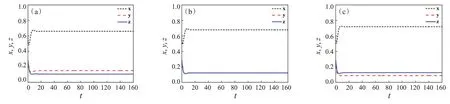
图4 系统(2)在β=1.31,α=1.33时的动力学行为时间序列图。(a)γ=0.1;(b)γ=0.55;(c)γ=1.22
第5种情况,β固定为1.31,当α的值小于β的值时,在此固定为0.87,γ值变化。当中间物种Y对食饵X的捕食率α小于捕食者Z对X的捕食率β,且捕食者Z对Y的捕食率为较低值时,γ=0.1,如图5(a)所示,Z存活而Y在t=137.0时灭绝;当捕食者Z对Y的捕食率变为γ=0.55时,如图5(b)中所示,Z因为对Y的捕食率的提高而加速了Y的灭绝,Y在t=55.4时就已经灭绝了。
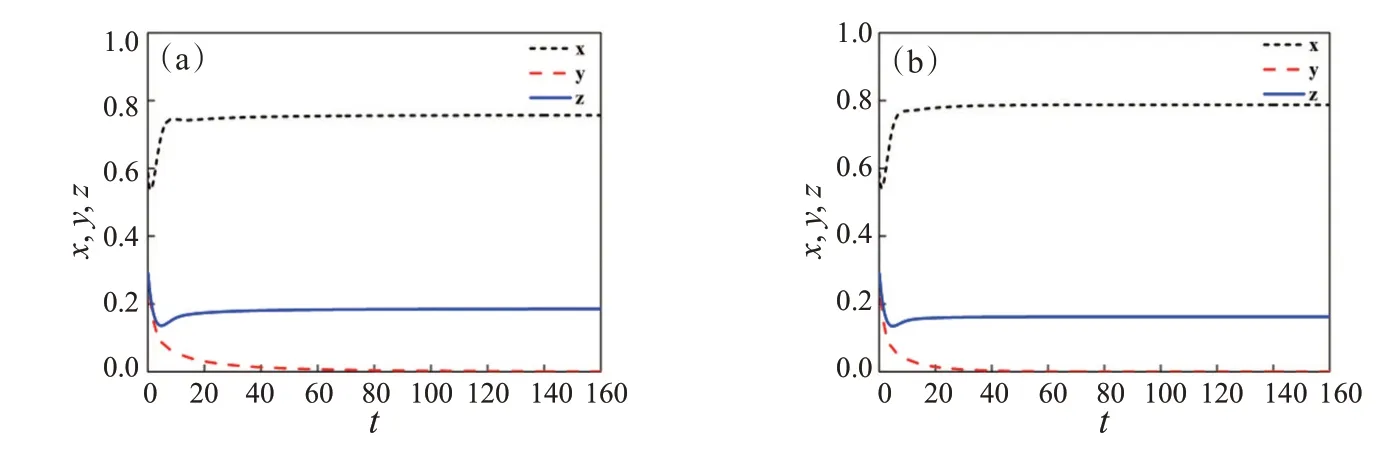
图5 系统(2)在β=1.31,α=0.87时的动力学行为时间序列图。(a)γ=0.1;(b)γ=0.55
第6种情况,β固定为1.31,当α大于β时,设为2.11,γ值变化。当中间物种Y对食饵X的捕食率α大于Z对X的捕食率β,Y总会存活,而Z可能灭绝或存活,如图6(a)和(b)中红色破折线和蓝色实线所示。如果Z对Y的捕食率较低,如γ=0.1,Z灭绝,如图6(a)中蓝色实线所示;如果Z对Y的捕食率提高,γ=0.55时,则Z因为对Y的捕食率的提高而从灭绝转为幸存,如图6(b)所示,形成了三物种共存的情况。
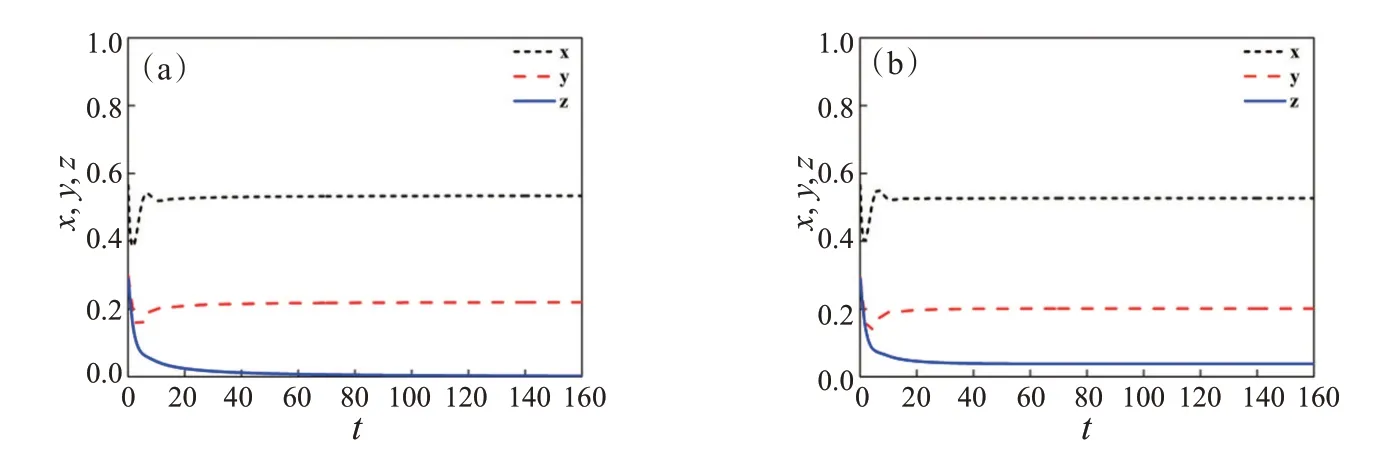
图6 系统(2)在β=1.31,α=2.11时的动力学行为时间序列图。(a)γ=0.1;(b)γ=0.55
以上讨论表明,数值模拟结果与理论分析一致。捕食者与食饵常常相互影响彼此的进化。捕食者倾向于选择增强发现和捕捉食饵的能力,而猎物则选择增强躲避捕食者的能力。正是因为这样,使得捕食者的捕食率产生变化,也因此影响了食饵与捕食者种群密度的动态变化[14]。影响捕食者捕食率的另一个因素可能是现有的环境,环境也许会干扰捕食者的觅食活动。此外,捕食者的运动特性对于成功定位食饵的方位也可能具有重要意义[15]。
4 结论
综上所述,我们在传统的食饵-捕食者模型中引入一个新的中间物种,建立了食饵、中间物种、捕食者三者之间的数学动力学模型。数值模拟结果表明,如果中间物种和捕食者对食饵的捕食率α和β大致相同,那么这三个物种可以共存。但是,当捕食者对中间物种的捕食率γ为较低值时,中间物种的种群密度大于捕食者的密度;当γ为中等大小时,中间物种和捕食者的种群密度近似相等;当γ为较高值时,中间物种的种群密度小于捕食者。如果中间物种对食饵的捕食率α大于捕食者对食饵的捕食率β,那么当捕食者对中间物种的捕食率γ为较低值时,中间物种幸存,捕食者灭绝;当γ提高时,捕食者也会幸存,从而形成三物种共存的情况。如果中间物种对食饵的捕食率α小于捕食者对食饵的捕食率β,那么当捕食者对中间物种的捕食率γ为较低值时,捕食者幸存,中间物种缓慢灭绝;当γ提高时,捕食者幸存下来,而中间物种就灭绝地更为迅速了。
