喷管尺寸对电弧风洞流场和热环境的影响分析
2021-03-13罗万清梁剑寒杨远剑赵金山孙海浩
罗万清,梁剑寒,杨远剑,赵金山,孙海浩
(1.国防科技大学高超声速冲压发动机技术重点实验室,长沙 410073;2.中国空气动力研究与发展中心超高速空气动力研究所,绵阳 621000;3.哈尔滨工业大学航天学院,哈尔滨 150080)
0 引 言
飞行器以高超声速在大气中飞行时,其前端空气经强激波压缩形成高温高压气体,分子热运动剧烈,导致气体分子出现振动激发、离解甚至电离等复杂物理化学现象,这种偏离完全气体的效应即为“高温真实气体效应”[1]。在严酷的气动加热环境下,飞行器表面温度会急剧升高,进而影响到材料和结构性能,若不采取合理的热防护措施,将产生不可估量的严重后果。美国历史上航天飞机的两次失事都与气动加热与热防护有关,可见高超声速飞行器防热的重要性。因此,防热材料与防热结构性能考核是高超声速飞行器研制中必须考虑的关键环节[2]。
地面风洞试验作为空气动力学三大研究手段之一,在空气动力学基础研究、飞行器研制、材料性能考核等诸多领域发挥着不可替代的作用。风洞设备类型很多,功能各异,针对的研究问题也不同。在众多模拟高超声速流动的设备中,电弧加热风洞有效运行时间长,同时可以提供较高焓值,可用于开展结构部件或材料热响应等试验研究,成为高超声速飞行器热防护系统(Thermal protection system, TPS)研制中地面热考核试验的主力设备。在航天飞机、太空飞船返回舱等诸多飞行器热防护系统的研制过程中,利用电弧风洞开展了大量的地面试验,发挥了重要作用[3-5]。然而,多数情况下风洞试验还不能完全复现飞行器的真实飞行环境,所以在开展试验时须根据关注的问题在几何相似、运动相似、物理相似等几方面做出取舍,进而选择合适的地面风洞模拟参数、试验模型尺寸等[6]。此外,风洞试验运行成本高,试验周期长,一定程度上限制了飞行器热防护系统的研制进程。探索提高风洞试验模拟的有效性,缩短试验周期,降低试验运行成本是研究者长期以来追求的目标。
收缩扩张喷管是超声速风洞的重要部件,其主要功能是加速风洞试验气体,提供模拟飞行器高速飞行所需的高速气流。如果风洞试验需要模拟飞行状态的马赫数,在开展试验时通过更换喷管实现(如激波风洞、常规高超声速风洞)。在喉道尺寸一定的条件下,增大出口的尺寸,一方面可以在试验段实现更高的气流马赫数,另一方面可以针对尺寸更大的模型开展试验。对电弧风洞而言,需要模拟典型位置的热流和材料内部热响应,一般要求模型不进行缩比,所以喷管出口尺寸限定了试验件的大小,而且通常情况下在模拟焓值、热流时不能同时实现和飞行状态一样的马赫数。如何根据飞行状态和地面风洞设备条件,更好地设计热考核试验提高试验模拟有效性和试验效率,或者设计喷管拓展现有设备的模拟能力,有必要开展不同尺寸的喷管对电弧风洞试验流场和试验模型表面热载荷等的影响研究。
利用计算流体力学(Computational fluid dynamic, CFD)手段模拟高焓气体流动,在控制方程中需要考虑化学反应以及热力学非平衡效应,传统的完全气体假设不再适用。Candler[7]和Gnoffo等[8]较早开展了高超声速热化学非平衡流场模拟,详细介绍了流动控制方程及相关热化学模型和输运特性,Bradley等[9]研究了高超声速喷管和激波的化学和振动非平衡流动模型,Knight等[10]对采用不同气体模型和不同计算方法预测高超声速气动热的能力进行了评估。国内,蔡国飙等[11]采用数值方法对双组元姿控发动机喷管化学反应流场进行了模拟,曾明等[12]研究了不同热化学模型对高超声速喷管流场的影响,丁明松等[13]研究了热化学模型对高超声速磁流体控制数值模拟的影响,程晓丽等[14]采用数值方法模拟了电弧风洞内无烧蚀球锥全目标绕流场,分析了来流非均匀性的影响。
将计算流体力学方法与电弧风洞试验手段结合开展气动热和热防护研究,一方面可利用风洞试验测量数据验证数值方法的可靠性,改进高焓流场数值模拟方法,另一方面通过对风洞试验高焓流场的数值模拟,可以分析试验模拟参数的有效性,预估试验流场以减少设备调试次数,为试验设计、喷管外形优化等提供指导。本文采用数值模拟方法,针对中国空气动力研究与发展中心(China Aerodynamics Research and Development Center, CARDC)20 MW电弧风洞不同尺寸出口的锥形喷管,开展电弧风洞高焓试验流场模拟,比较分析喷管尺寸对流场和驻点模型表面热流的影响规律。
1 电弧风洞设备
电弧风洞由供电供气系统、电弧加热器、收缩扩张喷管、试验段、扩压器、真空系统以及数据采集系统等组成,图1为中国空气动力研究与发展中心的20 MW电弧风洞[15]。

图1 中国空气动力研究与发展中心的20 MW电弧风洞
电弧加热器在高电流电压下对通过的试验气体进行加热,产生高焓、高压的混合组分气体,通过收缩扩张喷管膨胀产生具有高焓化学活性的超声速流动进入风洞试验段,针对不同试验模型开展气动加热试验、防热材料考核、防热材料催化效应以及高温真实气体效应等研究。在试验过程中通常是采用水冷校准模型(模型和传感器都为金属),对流场进行调试校准,在获得目标参数的情况下,再更换没有安装传感器的试验模型,采用相同状态的试验流场进行热考核试验。
在电弧风洞上开展热考核试验时,试验气体经电弧加热器加热后在收缩-扩张喷管入口已经处于高焓状态,气体组分的振动能以及电子能被激发,产生离解甚至电离反应,导致传统的完全气体假设在求解高焓流场时不再适用。这种情况下,在喷管流向不同位置,由于流动特征时间相比化学反应特征时间量级不同,流动处于不同的流动状态。如图2所示,流向为自左向右,在上游为平衡流动,中间区域为非平衡流动,下游为冻结流动,即在喷管出口试验气体仍然处于高度离解状态,这和飞行条件下的来流气体组分明显不同[16]。
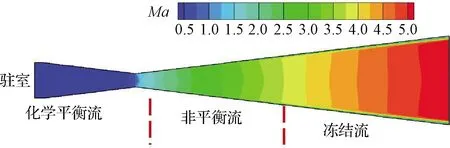
图2 喷管内部高焓流动状态示意图
风洞喷管喉道尺寸直接影响试验气体质量流率,进而影响可实现的气流总焓和需要的电弧加热净功率,估算公式如下[5]:
H0=1.679×106×(103p0Aeff/G)2.519
(1)
Pnet=H0G
(2)
式中:H0,p0分别为气流总焓和总压,Aeff为喷管喉道有效面积,G为气流质量流量,Pnet为净功率。
由式(1)和式(2)可知,电弧风洞喷管喉道面积受加热器功率、设备允许的总压、焓值、试验气体流量等限制,可以调整的幅度相对较小。保持喉道尺寸不变,在满足设备承受能力的条件下,如果喷管出口过小,试验段允许安装的模型尺寸就小,而且可实现的气流马赫数和飞行状态差异大,导致壁面附近流场参数、模型表面压力等与飞行条件之间的差异大,如果出口过大,到达试验段的气流的能量密度低,不能满足模型典型位置的热流要求。
2 数值方法
通常情况下气体转动能量激发的温度很低,容易与平动能量达到平衡,可以用一个温度(平动温度)来描述气体组分的平动能和转动能,而不同组分的振动能和电子能处于平衡状态,用另一个温度(振动温度)描述。这样高焓热化学非平衡流动控制方程包括多个描述质量守恒的组分质量方程,三个描述动量守恒的动量方程和分别描述总能和振动能守恒的两个能量方程。三维笛卡尔坐标系下,考虑热化学非平衡源项的两温度Navier-Stokes方程如下[17]:
(3)
式中:Q为守恒变量;t为时间;E,F,G和Ev,Fv,Gv分别为x,y,z三个方向的对流项和黏性项;S为非平衡源项。守恒变量、非平衡源项以及x方向的对流项和黏性项表达式如下:
Ev=
(4)

化学反应动力学方程为:
(5)
式中:r为化学反应序号,m为化学反应数目,αs,r和βs,r分别为反应物和生成物的化学当量系数,As为参与反应的第s个组分的分子式。
控制方程源项中第s个组分的质量生成率表示为:
(6)
式中:Ms为组分s的摩尔质量;Rf,r和Rb,r分别为第r个反应的正向和逆向反应速率。化学反应速率常数由Gupta模型获得[18],基于优先离解概念,Park建议求离解反应速率采用当地平动温度和振动温度加权函数(如几何平均)作为控制温度[19]。
由于电离程度很低,振动能源项只考虑平动-振动能量松弛项和组分生成项引起的振动能量变化,振动能源项表示为[17]:
(7)
振动能和平动能之间的交换采用Millikan和White修正的Landau-Teller模型,表达式如下:
(8)
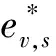
混合气体的黏性系数和热传导系数采用Wilke混合律方法计算,其中各组分的黏性系数和热传导系数分别由Blottner模型和Eucken关系得到,组分扩散系数通过双组分扩散近似简化公式获得[20]。
采用基于结构网格的有限体积方法离散求解高焓流动控制方程,无黏通量采用改进的Steger-Warming矢通量分裂格式计算[21],网格界面上的变量通过MUSCL插值重构以提高精度,而黏性通量采用中心格式计算。时间推进采用LU-SGS隐式方法,通过局部时间步长加速收敛。
在喷管入口给定驻室总焓和总压,由热力学平衡条件根据总焓和总压获得气体总温和组分质量分数[22],通过Riemann不变量求得边界上的其它参数。对超声速来流边界,直接赋来流参数,超声速出口边界参数由内场外推。由于风洞喷管和涉及的试验校准模型都是金属材料,且试验中采用了水冷措施,故壁面采用等温壁边界条件,温度取300 K,化学反应采用完全催化边界条件。
利用建立的方法对电弧风洞高焓流场进行了模拟验证,比较发现对试验模型和风洞喷管出口轴向距离较近的状态,采用喷管内流和模型绕流分开模拟是可行的[15]。通过对不同热化学非平衡模型比较发现,在相同的温度模型条件下,采用5组分和7组分空气化学反应模型获得的试验模型表面热流接近,而双温度模型计算结果相比单温度模型更接近试验测量值。采用5组分双温度模型对不同试验模型多个试验状态进行了模拟,表面热流的计算值和试验测量相对误差都在15%以内,说明数值方法具有很好的可信度[15]。兼顾可靠性和计算效率,文中选用5组分双温度模型对高焓流场进行模拟。
3 结果与讨论
采用数值方法对三套不同尺寸的锥形喷管高焓流场进行模拟,利用出口参数作为来流条件求解试验段球柱模型绕流和表面气动热分布,比较分析不同尺寸喷管条件下的流场差异。
三套喷管入口和喉道直径相同,分别为80 mm和30 mm,出口直径依次为100 mm,200 mm,260 mm,前两套喷管的收缩角和扩张角都为7°,第三套喷管收缩角约为12°,扩张角为10°。文中以出口直径对喷管进行区分,以字母φ表示喷管出口直径。试验段球柱校核模型头部半径35 mm,长度50 mm。模拟状态为焓值16 MJ/kg,驻点完全催化冷壁热流5 MW/m2,通过计算获得的不同喷管试验状态参数见表1,其中喷管喉道有效面积以直径29 mm计算。以焓值和驻点热流接近作为限定条件通过数值模拟获得了对应的飞行状态,即飞行高度56 km,飞行速度5600 m/s。
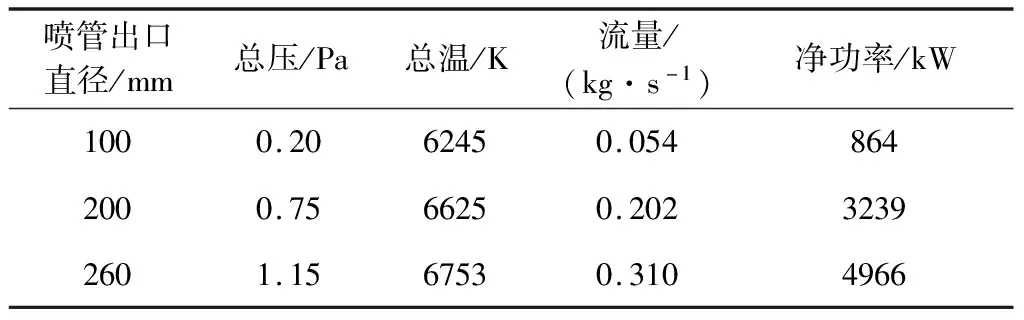
表1 不同尺寸喷管的试验状态参数
从表1可以看出,如果只是满足焓值和校核模型驻点热流,三套喷管中,出口尺寸越小,气流的总压和总温越小,同时质量流量和净功率也越小,且净功率差异非常明显。这说明选用出口尺寸大的喷管,虽然在试验段可以放置更大的模型,但是对加热器功率要求更高,可以推断在同样焓值和加热功率条件下可以实现的模型表面热流更小。如果在满足模型尺寸要求的条件下,选用出口直径小的喷管要求电弧加热功率更小,也就更节约试验运行成本。
如果流体微团中每种组分的内能对平动温度而言,以玻尔兹曼形式分布于各自的能级上时,则认为混合气体处于热力学平衡状态。相反,则认为流体微团处于热力学非平衡状态,这时平动温度和振动温度就存在一定差异[22]。图3给出了喷管内部对称面上振动温度与平动温度的差异比较,可以看出在喷管上游,两个温度差异不大,说明气流接近热力学平衡状态,而在下游尤其是靠近喷管出口区域,平动温度明显低于振动温度,说明气流非平衡程度较高。虽然不同喷管的膨胀段长度不同,气流的膨胀程度不同,但是在出口区域,采用三种尺寸喷管获得的平动温度与振动温度绝对差值接近,说明选用这几种尺寸喷管获得的试验段来流热力学非平衡程度接近。
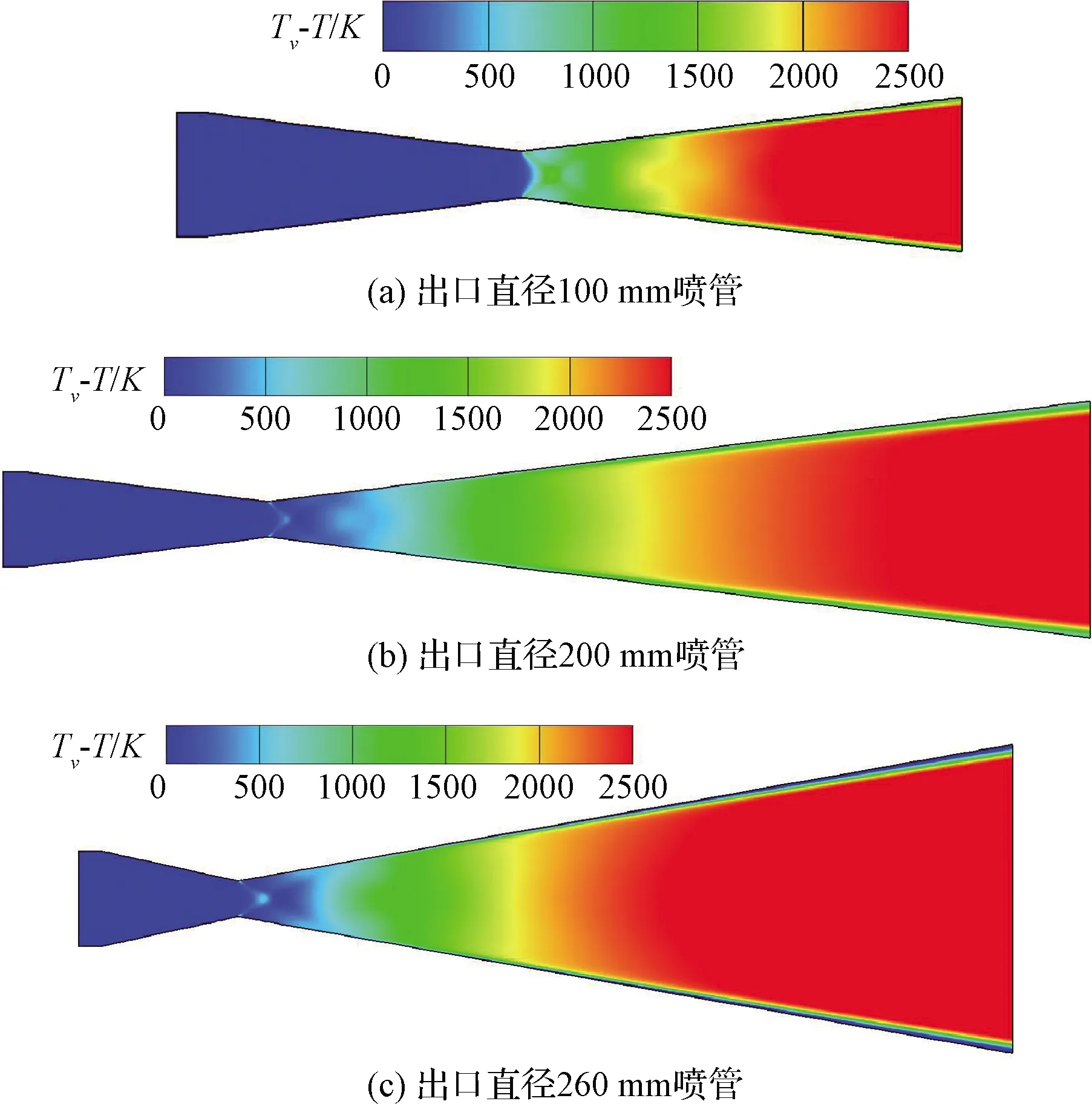
图3 对称面Tv-T分布比较
图4和图5分别比较了不同尺寸喷管出口径向分布的平动温度和轴向速度。比较发现,出口尺寸小的喷管,出口中心区平动温度更高,而轴向速度更低,这是因为在入口总温接近的条件下,尺寸小的喷管膨胀程度不如尺寸大的喷管充分,导致温度降低幅度和速度增加幅度不如尺寸大的喷管,使得出口尺寸小的喷管试验状态与飞行状态的来流温度和速度差异更大。
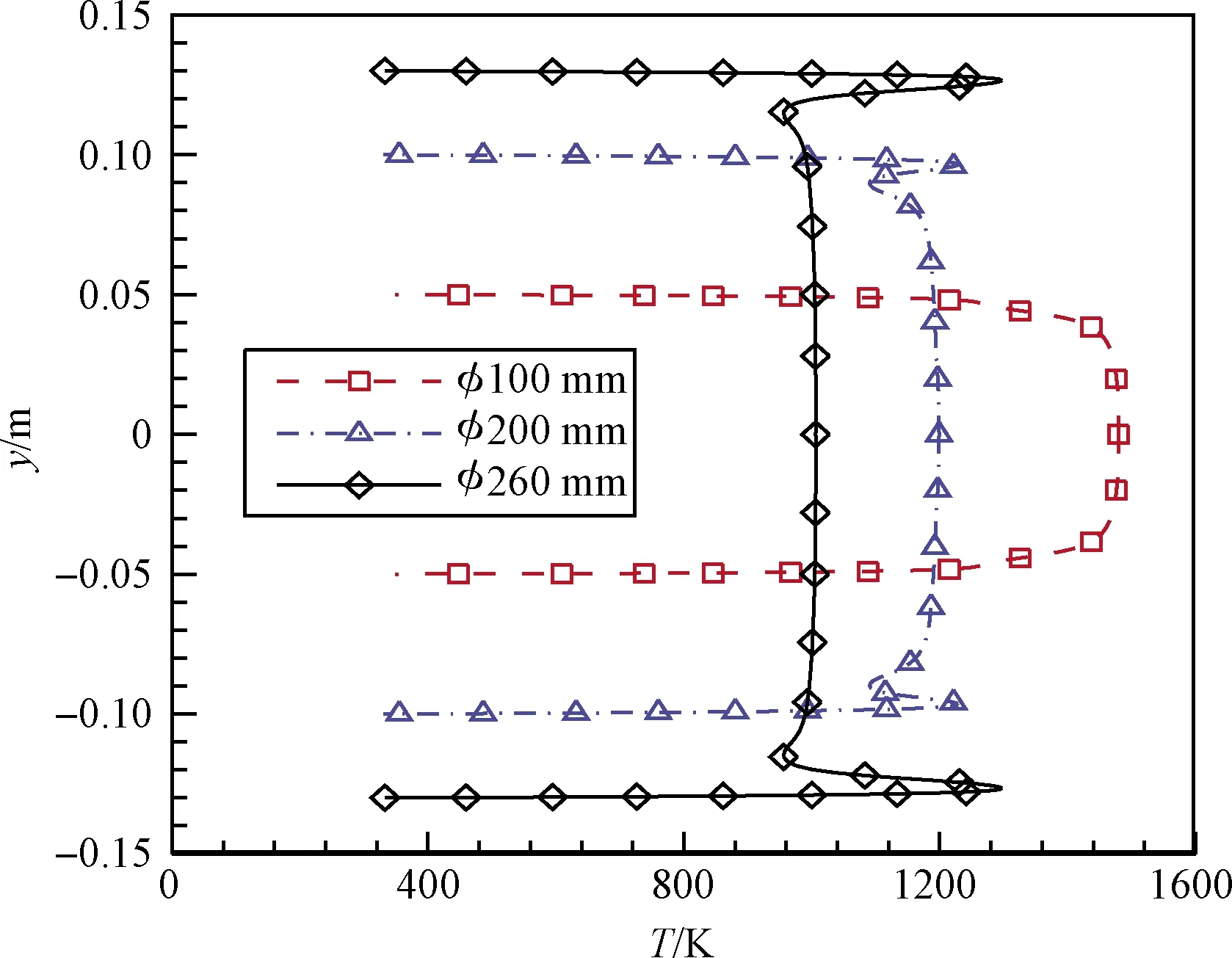
图4 喷管出口平动温度分布比较
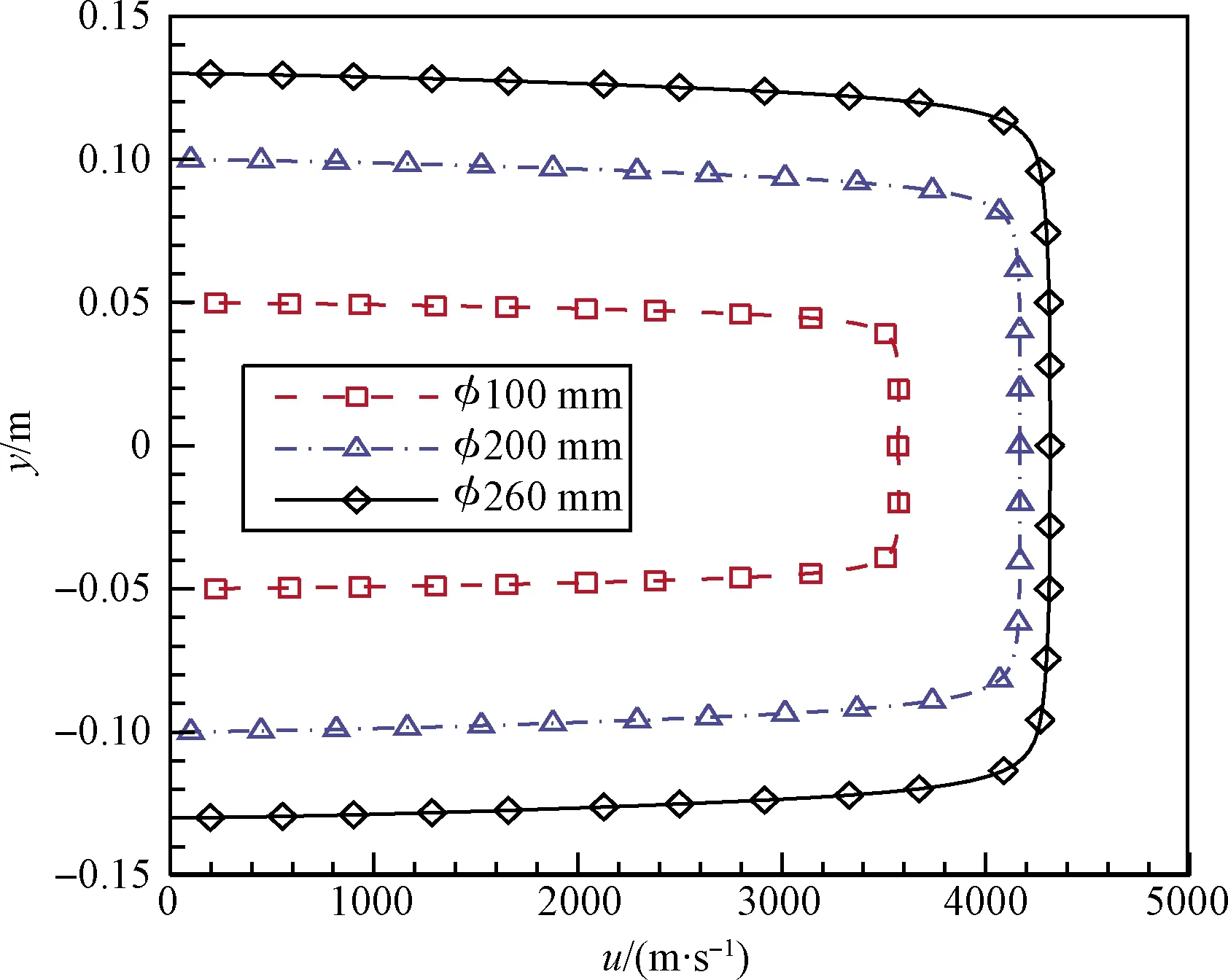
图5 喷管出口轴向速度分布比较
从量纲上分析参数ρuH0为流向截面单位面积上的能量流率,单位与热流相同,图6给出了喷管出口径向该参数的比较。从图6可以看出,出口尺寸小的喷管单位出口面积上的能量流率比尺寸大的喷管大,且都显著高于飞行状态(约为47 MW/m2)。由于下游试验段模型驻点的热流接近,说明就单位流向截面上的气流能量转化为模型表面气动热的占比而言,采用出口尺寸小的喷管获得的试验流场的转化率比尺寸大的喷管更低。也就是说,风洞试验中来流焓值和驻点热流与飞行状态接近的条件下,选择出口尺寸大的喷管,流向单位面积上能量流率与飞行状态差异更小。
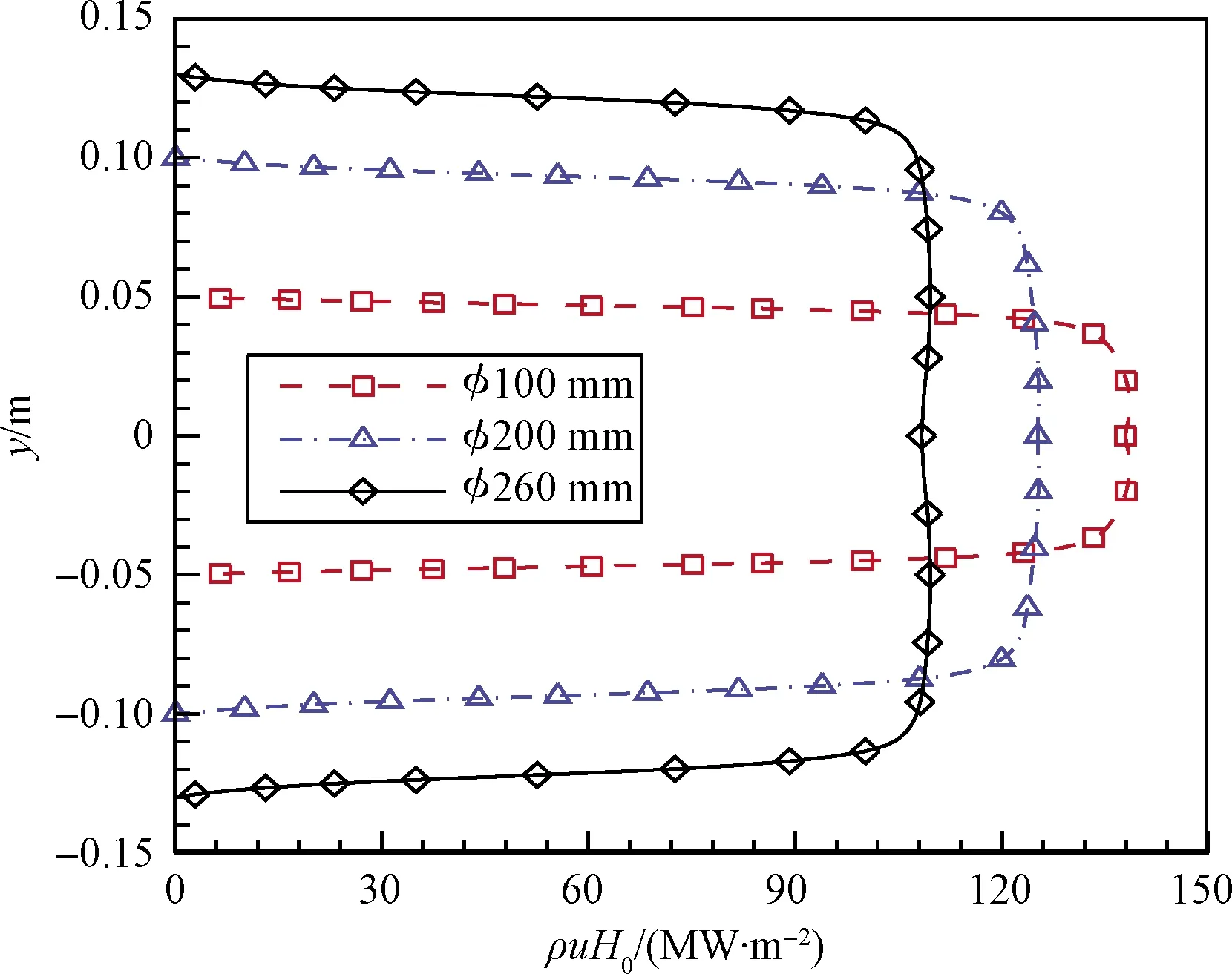
图6 喷管出口ρuH0分布比较
电弧风洞试验中,除了模拟焓值和典型位置热流外,有必要分析流场结构等与对应飞行状态的差异,下面将采用不同尺寸喷管获得的试验流场参数和壁面热流(表1中的试验状态)与对应飞行状态下结果进行对比分析,进一步了解风洞试验模拟的有效性。图7给出了模型绕流对称面上压力分布比较,图8和图9分别给出了驻点线上平动温度和氧原子质量分数比较,其中R为头部半径,“Flight”代表飞行状态,“Test”代表风洞试验状态。
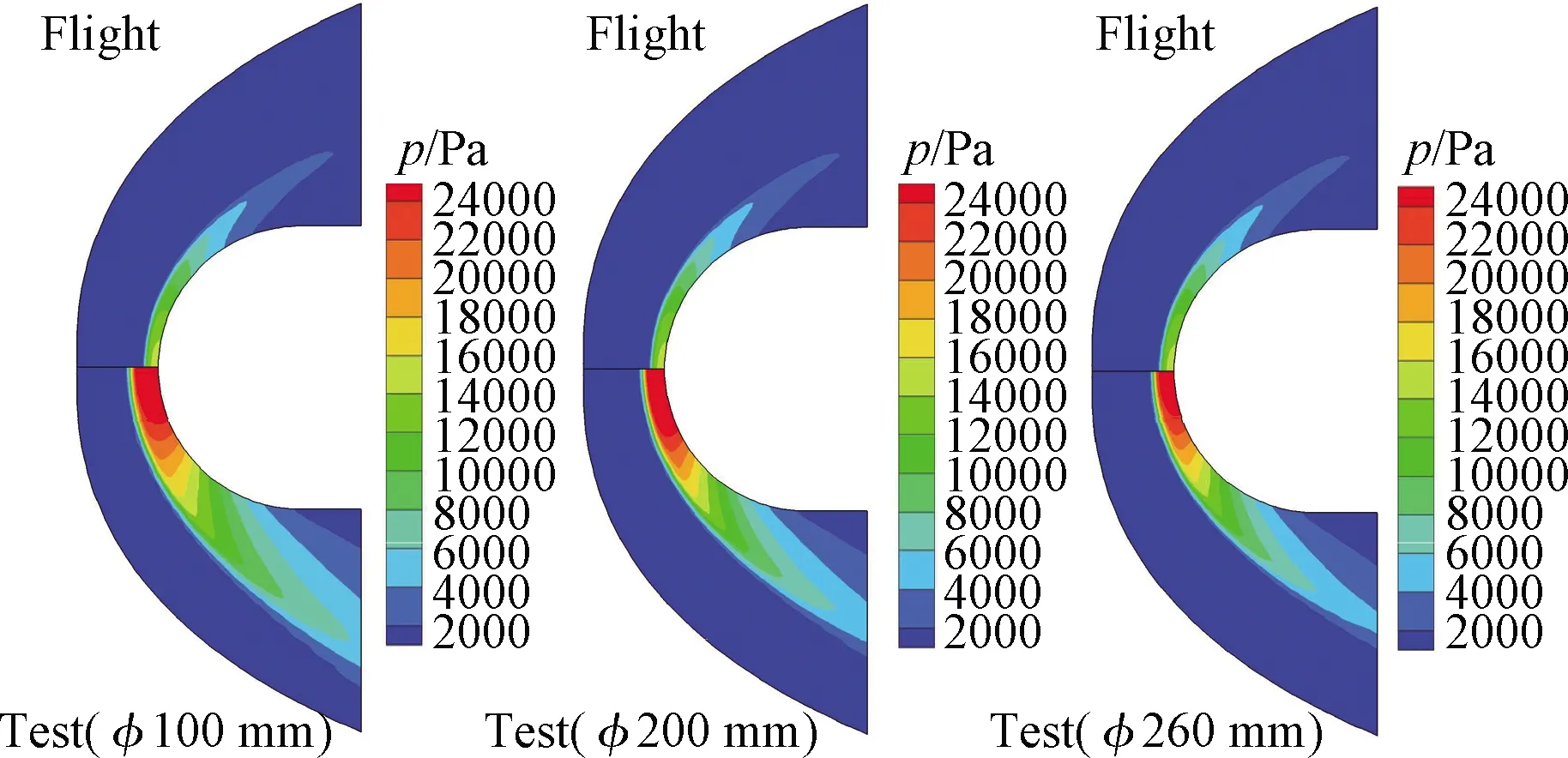
图7 球柱模型绕流对称面压力分布比较
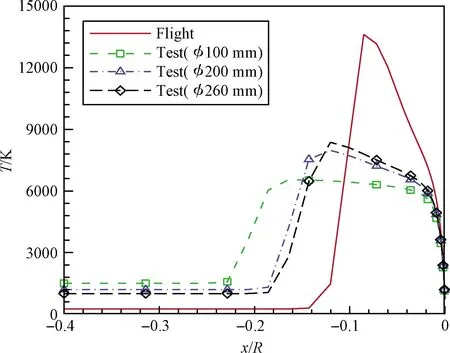
图8 驻点线上平动温度比较
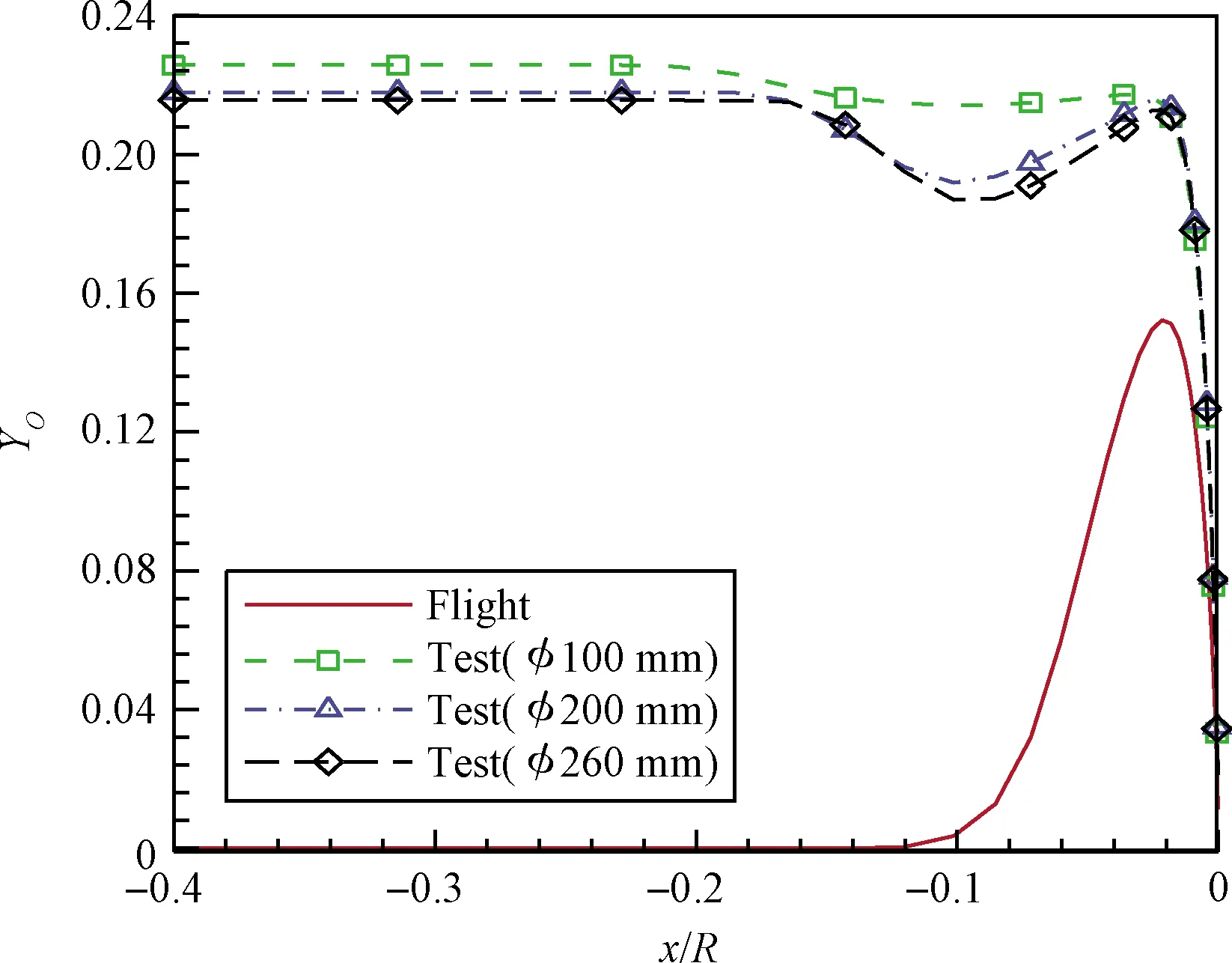
图9 驻点线上氧原子质量分数比较
从图7可以看出,不同尺寸喷管条件下风洞试验状态压力峰值(驻点区域)差异不大,都显著高于飞行状态,而不同喷管条件下激波脱体距离明显不同,这是由于喷管出口与喉道的面积比不同,导致试验段来流的马赫数不同,且马赫数相对飞行状态较低,导致激波脱体距离相比飞行状态更大。要缩小试验状态与飞行状态来流马赫数或头部激波脱体距离的差异,在设备能力允许范围内应尽可能选择出口尺寸大的喷管。
从图8可以看出,试验状态来流的平动温度高于飞行状态,且喷管出口越小,平动温度越高,而波后试验状态的平动温度低于飞行状态,且喷管出口越小,平动温度越低,这说明在文中模拟的状态下,出口尺寸大的喷管在驻点线上的平动温度与飞行状态差异小,这是由于喷管出口尺寸越大,出口气流马赫数越大,马赫数随即影响了激波前后的温度比值。由于风洞试验气体中氧气在上游就已经发生离解,所以试验状态来流氧原子质量分数明显高于飞行状态(飞行状态来流几乎不含氧原子),过激波时飞行状态驻点线上的氧原子质量分数显著增大,而试验状态变化幅度不大,但仍然是试验状态的氧原子质量分数比飞行状态更高,见图9。由于试验状态都处于高焓状态,气体中氧气离解都比较彻底,且在喷管下游处于冻结状态,故采用不同尺寸喷管获得的流场中心区氧原子质量分数差异不大。
图10和图11分别比较了模型表面总热流和传导热流分布,图中横坐标s为模型表面中心线上的点沿表面到驻点的距离。通过比较可以看出,驻点热流接近的情况下,整个模型表面的热流分布差异不大,包括不同尺寸喷管试验状态和对应飞行状态。就表面传导热流而言,采用不同喷管的地面风洞试验状态差异不大,而飞行状态相比试验状态偏大,尤其在驻点区,这说明试验状态下由化学反应导致的扩散热流更大。即总热流接近的条件下,飞行状态和风洞试验状态传导热流和扩散热流所占的比例有所不同,飞行状态的壁面法向温度梯度更大,所以模型表面传导热流更大,而地面试验状态壁面附近原子质量分数更大,由于复合反应放热产生的扩散热流更大。
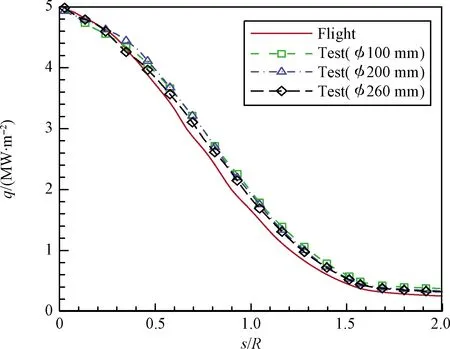
图10 模型表面热流分布比较
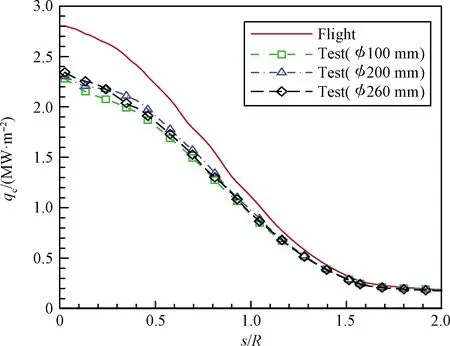
图11 模型表面传导热流分布比较
4 结 论
采用高焓流动数值模拟方法,求解了特定来流焓值和校核模型驻点热流条件下电弧风洞不同出口尺寸的锥形喷管内部以及试验段流场特性,分析了喷管尺寸对高焓试验流场以及模型表面气动热的影响规律,得到如下结论:
1)地面风洞试验可以通过不同尺寸喷管模拟相同的飞行状态焓值和模型典型位置热流,选用小尺寸出口的喷管要求的加热功率更低,更节约成本。即对相同尺寸的模型,在电弧加热器功率一定时,出口较小的喷管能够实现更高的热流,但单位流向截面上的气流能量转化为模型表面气动热的比例却更低。
2)对于不同出口尺寸的喷管,出口区域的高焓试验流场热力学非平衡程度接近,模型驻点区域压力、波后氧原子质量分数以及试验模型表面传导热流和扩散热流占比都比较接近。但是由于不同尺寸的喷管出口气流马赫数不同,试验段来流速度、激波脱体距离和驻点线上平动温度差异明显。
3)喷管出口尺寸越大,试验状态高焓流场的来流速度、波后平动温度以及激波脱体距离和飞行状态更接近,即采用大尺寸出口的喷管能够更好地模拟壁面附近温度梯度以及剪切力等。而对模型驻点区域压力、波后氧原子质量分数和表面不同类型热流占比,不同尺寸喷管的试验状态与飞行状态之间的差异都很明显。
