析构时间相关模型的面对称飞行器机动估计

卢晓东，辛佳宁，顾嘉耀，王俊康，程 承

(西北工业大学航天学院，西安 710072)

0 引 言

随着现代战斗机的空中机动能力不断增强，防空导弹为提高制导精度迫切需要对战斗机的大机动加速度实现有效估计。然而目前防空雷达对飞机目标的测量信息只有角度、距离和多普勒速度等，这些观测信息对飞机大机动过载的表征能力有限，因此对飞机机动加速度估计精度并不理想。现有对于空中非合作机动目标的估计研究主要集中在目标运动学精确建模和滤波估计方法的改进[1]。其中目标运动学建模是对目标飞行器飞行动力学的直接表述，因此是提升目标机动信息估计精度的最重要手段。

目前对于空中非合作机动目标的运动学建模方法主要归纳为两种方式：一种是将目标机动作为坐标系解耦的随机过程，采用统计学方法建模；另一种是考虑目标机动时的飞行动力学方程，将动力学、气动作用和大气模型简化得到目标运动模型[2]。

对于单纯使用统计学方法对目标机动建模的典型运动模型有：匀速运动(CV)模型、匀加速运动(CA)模型、Singer模型、Jerk模型和“当前”统计(CS)模型等。其中CV模型和CA模型简单地认定加速度为常值，难以描述目标的真实机动特性[3-4]；Singer模型、Jerk模型和“当前”统计(CS)模型将目标的加速度和加加速度近似为时间相关，这使得模型能较好地描述目标机动的统计特性[5-13]。这些模型虽然具有较好的通用性和覆盖性，但其完全忽视飞行器动力学中各通道间的耦合作用，因此空中目标进行大机动时难以满足其统计特性假设。

对于采用动力学方程建模的方法能够更加真实地描述目标的实际运动物理状态，从本质上说更具科学性，诸如匀速转弯(CT)模型就特别适合民航飞机匀速转弯的过程。但是由于空中非合作目标的动力学模型参数难以获取，因而这些模型参数通常作为待估状态量或者事先人为设定。近几年来，喻晨龙等[1]、王树亮等[14]、李凡等[15]、郭相科等[16]、张凯等[17]和Hough[18]等学者将模型气动参数作为随机变量利用统计学方法和神经网络等方法建模，实现了动力学模型参数的自适应调整，取得了较好的仿真效果。

文献[1]针对高临近空间高超声速滑翔目标，在雷达测量直角坐标系下引入纵向通道和横向通道的角度域模型，将倾角变化率和方位角变化率描述成零均值正弦自相关随机过程。文献[14]以CS模型为基础，引入神经网络和“记忆”模块，用感知信息熵来描述目标跟踪不确定性，实现了对目标运动参数的自适应调整。文献[15]以临近空间滑跃式高超声速目标为对象，在横纵向机动样式方面将气动加速度中的阻力与爬升加速度建模为二阶时间相关模型，使加速度自相关函数具备周期性与衰减性。文献[16]针对临空高速飞行器滑跃阶引入Sine模型的加速度正弦波的零均值随机过程，用于描述目标的规律跳跃。文献[17]针对高超声速滑翔目标将纵向和横向机动等效为一阶时间相关模型，并将对转弯和爬升参数和机动频率引入构建动力学交互多模型。这些方法是将飞行器动力学与统计学及智能感知技术相互融合，这有助于对高超飞行器大机动的跟踪研究。但是这些论文主要关注于高超飞行器的滑翔跳跃阶段机动，及类似正弦的周期性机动研究，而对于大气层内的面对称飞行器(飞机)目标的大滚转角机动缺少针对性研究。

本文针对上述建模方法未考虑飞行器动力学各通道耦合问题，基于面对称飞行器大机动过载主要取决于主升力面的滚转角和主升力的物理关系，提出对面对称飞行器动力学析构后简化为两个时间相关物理量(主升力面滚转角和主升力)，从而建立面对称飞行器的动力学析构时间相关模型(DTDM)。随后基于分段定常系统可观测性理论和奇异值分解法验证了该模型对飞行器大机动的可观测性优于现有方法。最后该模型结合容积卡尔曼滤波(CKF)对战斗机大机动时加速度估计进行了数学仿真校验。

1 面对称飞行器动力学析构降阶

本文以防空雷达对现代战斗机探测为应用背景，通过对目标飞行器进行动力学和统计学建模，实现对面对称飞行器大机动加速度的精确估计。考虑到防空雷达多为视距探测方式，探测距离一般在300 km以内，因此地面可近似为平面大地，且不考虑地球自转，即地面坐标系视为惯性坐标系。由于现代战机大机动主要通过改变飞行器主升力面滚转角和主升力面上的气动力来实现，因此面对称外形战机的机动过程中受力关系如图1所示。

图1中Oxyz为惯性坐标系(同地面坐标系)，G为重力，方向铅垂向下。Ox3y3z3为飞行器速度坐标系，γV为飞行器速度滚转角(即主升力面滚转角)，气动力在速度系下分解为主升力面升力Y、侧向力Z和阻力X。根据现代战机的飞行特点，其侧滑角很小，故可忽略侧向力Z，战机巡航时的发动机推力P与阻力X基本平衡。因此飞行器的大机动过载主要取决于主升力Y和重力G的作用，其中主升力的大小Y(t)和速度滚转角γV(t)可近似写为如下函数：

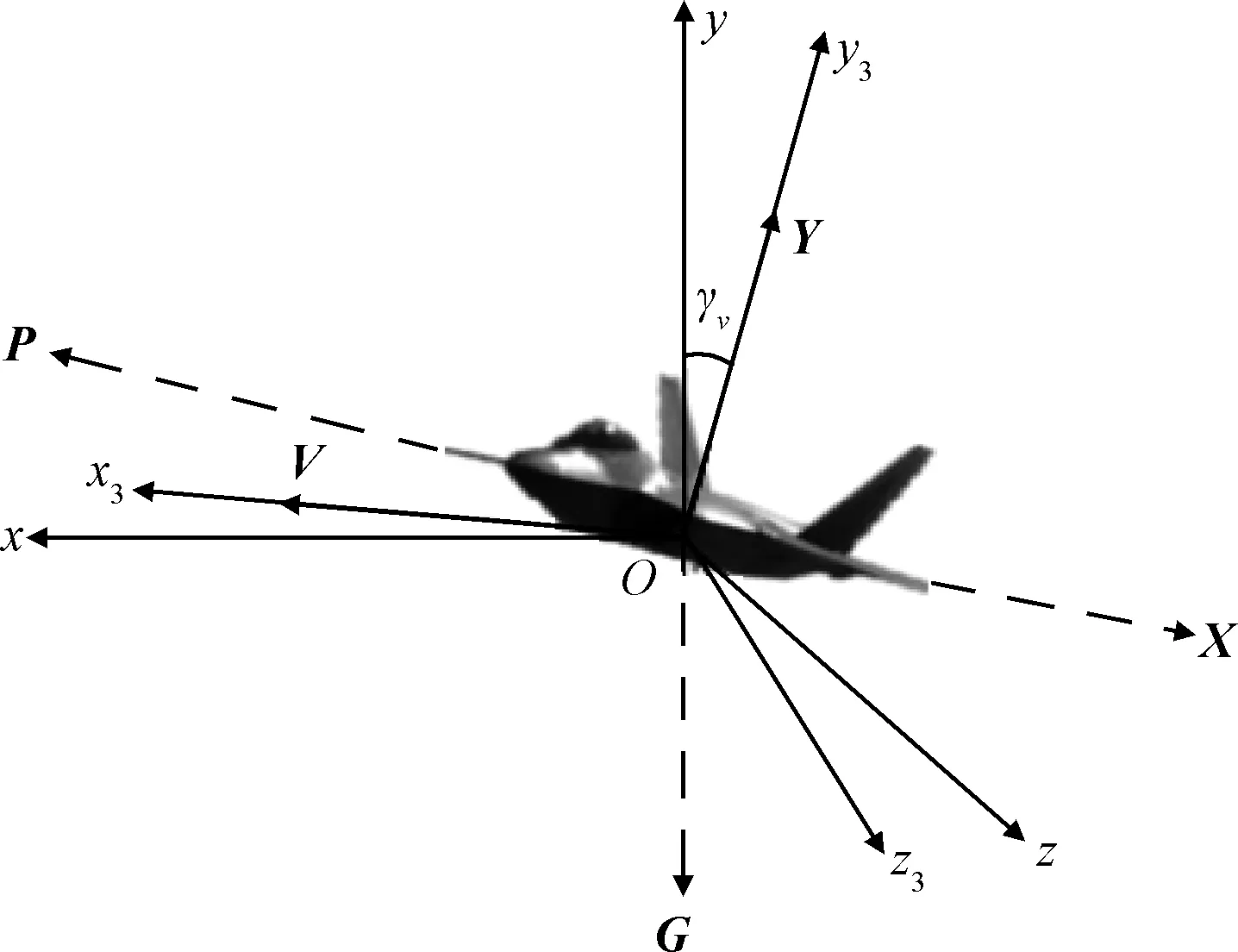
图1 面对称飞行器的机动受力关系图

(1)

(2)

为避免对这些不确定参数的估计，本文对式(1)和式(2)采用析构方法进行简化。考虑到在短时间内气动参数可近似为常值不变，各个姿态角、气动攻角和舵偏角在滤波周期内的变化连续且变化范围有限。因此可以近似假设速度滚转角和主升力为宽平稳随机过程，那么根据速度滚转角的时间相关函数RγV(τ)写为指数形式为

(3)

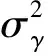
主升力面气动力Y(t)可等效为主升力过载N(t)，则其时间相关函数表示为

(4)

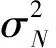
将速度滚转角和主升力面过载的时间相关函数采用Wiener-Kolmogorov白化为输入为白噪声的一阶时间相关模型，则N(t)的时间相关模型为

(5)

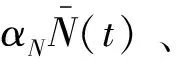
γV(t)的时间相关模型为

(6)

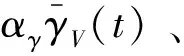
至此通过“当前”统计模型近似描述主升力过载N(t)和速度滚转角γV(t)的变化规律，从而将纵向和侧向平面的受力综合考虑，能够更好地描述面对称飞行器的机动特性，从而实现对目标飞行器机动趋势的估计。

2 面对称飞行器的运动模型建立

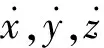
(7)

由此构建目标飞行器运动状态量更新方程为

(8)

式中：ax(t),ay(t),az(t)是目标飞行器在地面坐标系下的加速度，其为待估变量。现有的Singer模型、Jerk模型和CS模型都是将其等效为噪声或相关过程，这种假设只是统计学和随机过程中的近似，因此对强机动目标估计时往往效果不佳。

本文的创新点正在于通过将γV(t)和N(t)引入三个加速度的动力学关系，从而在动力学层次上构建ax(t),ay(t),az(t)的演化关系。由于速度滚转角γV(t)和主升力过载N(t)是在飞行器速度坐标系下描述，因此需要推导至地面坐标系，并与地面系下的加速度建立约束关系。

在飞行器速度坐标系下，由气动力和推力产生的合加速度atV可近似表示为

(9)

式中：g为重力加速度。

将速度系下的合成加速度atV通过坐标转换到地面坐标系，并考虑重力加速度g后得到目标实际加速度ag为：

(10)

(11)

(12)

其中弹道倾角θ和弹道偏角ψV可由状态变量解算：

(13)

3 面对称飞行器的机动滤波方程

根据上述推导可得到面对称飞行器在地面坐标系下的离散状态方程以及测量方程。

1)目标运动模型的离散状态方程

假设雷达采样周期为T，将连续时间离散化，可得面对称飞行器的离散状态方程为

X(k+1)=F1X(k)+F2{f[X(k)]}+

w(k)=φ[X(k)]+w(k)

(14)

式中：

其中，f[X(k)]的下角标表示f[X(k)]的某行到某行，如f[X(k)][4～6]表示f[X(k)]的第4行到第6行，w(k)为系统噪声。

2)主动式雷达的离散量测方程

假设测量雷达为地面静止雷达，在地面坐标系下对目标飞行器进行主动式测量，可获得目标与雷达的径向距离r，目标高低角ε和目标方位角β。则观测方程中非线性量测函数H[X(k+1)]为：

H[X(k+1)]=

(15)

则系统的量测方程Y(k+1)可表示为：

(16)

式中：r为雷达与目标的径向距离，ε为高低角，β为方位角；ν(k+1)=[nr(t),nε(t),nβ(t)]T为量测噪声，包含雷达的距离、高低角和方位角测量噪声。

4 可观测性分析

由于系统的可观测性会影响滤波的精度，为确保DTDM模型滤波精度，下面对模型中各个状态量的可观测性进行分析。考虑到系统的可观测性与系统噪声和观测噪声无关，故使用齐次系统方程讨论DTDM模型的可观测性。齐次系统模型如下：

(17)

首先求取非线性函数φ(·)和H(·)的雅克比矩阵，将系统近似线性化，再根据分段定常系统(PWCS)可观测性理论和奇异值分解法(SVD)[20]对系统的可观测性进行分析，得到系统的提取可观测矩阵(SOM)在不同目标机动加速度下的奇异值。

表1 SOM在不同目标机动加速度下的奇异值

下面将本文所提出的动力学析构时间相关模型(DTDM)与文献[11]中的改进“当前”统计模型(MCSM)和Jerk模型进行可观性对比。下面给出目标飞行器机动最大加速度为9g时，DTDM,MCSM和Jerk模型的系统提取可观测矩阵的奇异值，结果如表2所示。

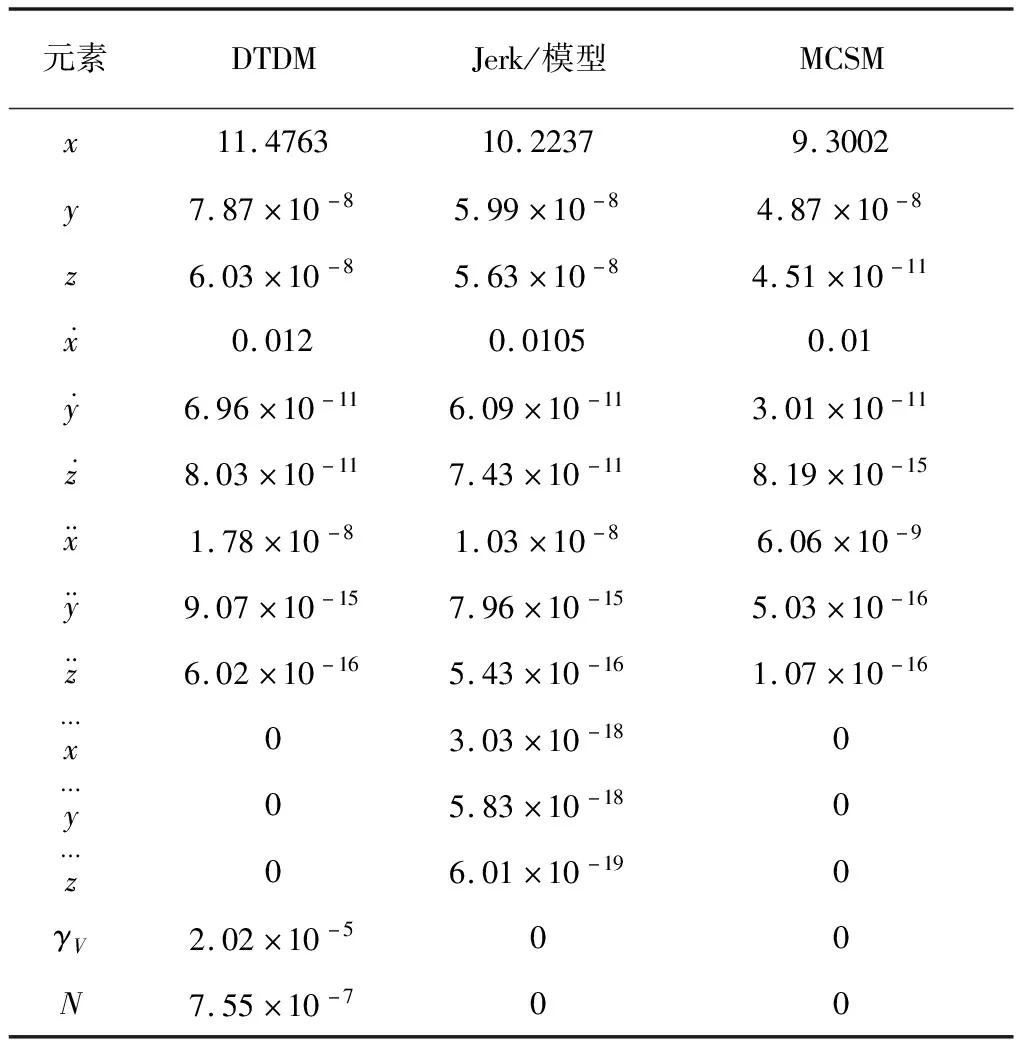
表2 不同模型的可观测矩阵奇异值

从可观性结果分析可以看出，在目标加速度均为9g时，DTDM系统对目标飞行器运动信息的可观测性更高，尤其是对目标加速度的可观测性要明显优于其余两个模型。这也从可观性方面验证了本文提出的DTDM方法对目标飞行器机动信息进行估计要比基于MCSM和Jerk模型的方法更具优势。

5 仿真校验

本文以现代战斗机进行典型躲避机动为例进行跟踪，假设目标最大机动加速度为9g，飞行初始速度为[200 m/s,0,0]，初始位置为[0,5000 m,0]，目标真实飞行轨迹如图2所示。

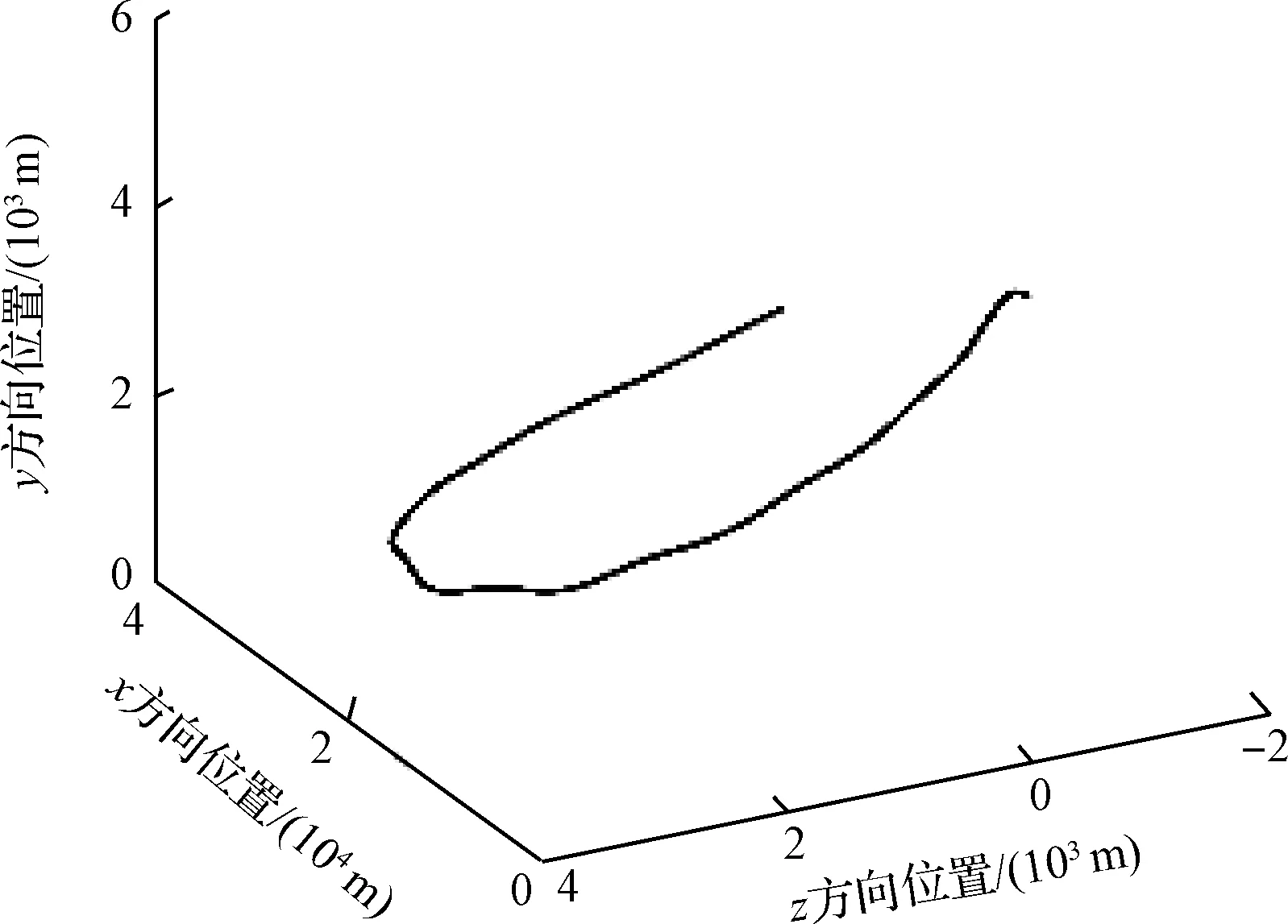
图2 目标真实飞行路径

仿真时导弹初始地面直角坐标系位置为[30000 m,5000 m,3000 m]，在地面系下的初始速度为[-700 m/s,0,-100 m/s]，雷达采样时间为0.01 s，量测距离误差标准差σr=5 m，高低角和方向角的量测误差标准差σε=σβ=0.1°，用MCSM和Jerk模型与DTDM进行对比仿真。MCSM取机动时间常数为10，Jerk模型取机动时间常数为15，DTDM取机动时间常数为12，滤波方法使用CKF，蒙特卡洛次数N=50。以各个状态的估计误差均方根(RMSE)来衡量估计精度：

(18)

图3为DTDM对面对称飞行器主升力面滚转角和主升力过载产生的机动加速度的跟踪曲线。

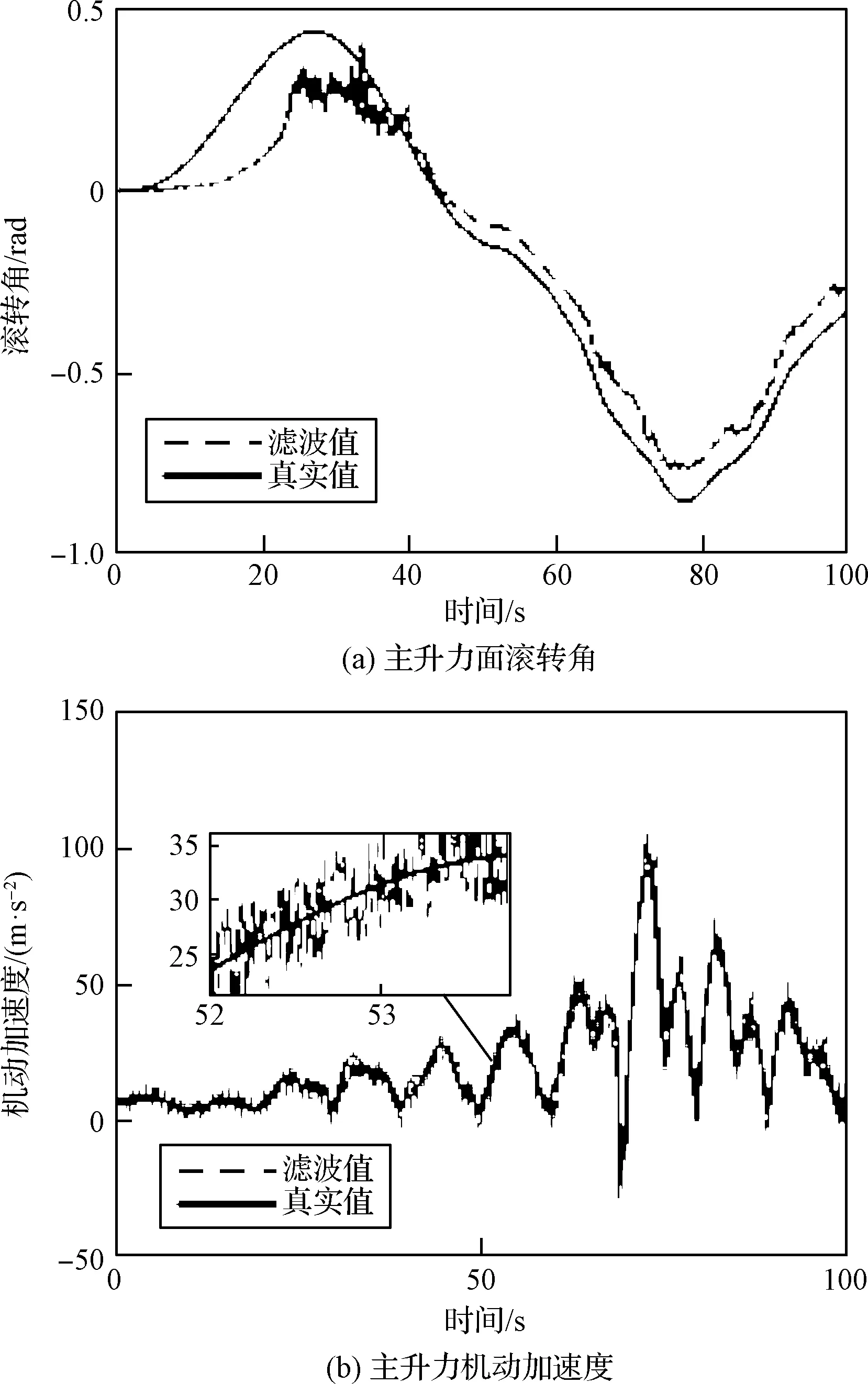
图3 主升力面滚转角和主升力机动加速度跟踪曲线

图3显示DTDM对主升力过载产生的机动加速度能够较好跟踪，而对目标主升力面滚转角估计虽有延迟，但对其变化趋势仍有较好跟踪。为直观比较各模型的估计精度，表3给出各运动模型位置、速度和加速度估计误差的多次仿真最大值的均方根。

图4给出了目标在地面系下三方向加速度的估计误差均方根，为显示清晰在画图时进行了数据稀疏化。图4显示在目标机动变化较小时，DTDM对加速度估计精度和MCSM及Jerk模型相当；在80～100 s之间，y轴和z轴上有强机动时，DTDM对加速度估计精度比MCSM和Jerk模型都高。这是因为MCSM没有考虑加加速度变化，只是对加速度上限进行了自适应；而Jerk模型考虑了加加速度影响，但将其描述为零均值的时间相关模型。DTDM则考虑了面对称飞行器的主升力面过载与滚转角之间的耦合约束关系，而非单维度的统计学关系；其次DTDM将主升力过载和滚转角作为非零均值相关模型，其理论精度阶数不小于Jerk模型。此外从表3可以看出，在目标机动为9g的时刻，DTDM对加速度估计误差相比其他方法要小一半以上。

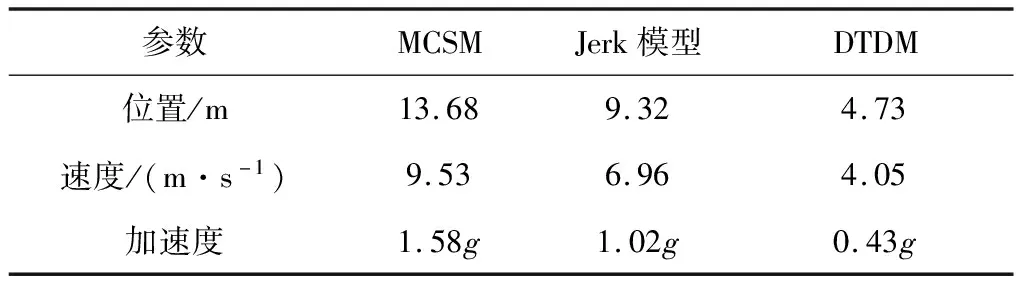
表3 不同模型的位置、速度和加速度估计误差最大值的均方根

图4 加速度估计误差均方根

6 结 论

本文针对面对称飞行器提出了一种利用动力学模型析构降阶构建的时间相关运动模型(DTDM)。其利用时间相关过程和飞行器动力学分解方式构建了动力学析构时间相关运动模型，并根据分段定常系统(PWCS)可观测性理论和奇异值分解法(SVD)对该模型的可观测性进行分析，分析结果表明其可观性优于“当前”统计运动模型及其改进模型。最后针对现代战机的典型机动轨迹进行了仿真校验，仿真结果表明采用DTDM对面对称飞行器的机动加速度估计精度高于改进“当前”统计模型和Jerk模型。这种对空中大机动目标的机动加速度的较精确估计，将有利于提高防空导弹拦截目标时的制导精度。