探月返回飞行器跳跃式再入轨迹优化

赵吉松，王江华，王泊乔，张金明，朱航标

(1.南京航空航天大学航天学院，南京 210016；2.北京机电工程研究所，北京 100074)

0 引 言

再入返回技术是载人航天飞行的关键和难点之一。与从近地轨道返回不同，月球探测器的返回速度高达11 km/s，火星探测器的返回速度高达14.5 km/s。对于如此高的返回速度，飞行器如果采用直接再入的方式返回地球，最大过载高达17以上，远远超出了人的承受能力。跳跃式再入是减小最大过载的一种有效途径。如图1所示，飞行器以较小的再入角进入大气层，减速的同时利用大气提供的升力，跳出大气层，在大气层外作一段椭圆轨道飞行，然后重新再入大气层[1]。这种跳跃式再入方式通过两次再入减速，延长了减速时间，从而能够减小飞行器再入过程的最大过载和最大热流等[2]。

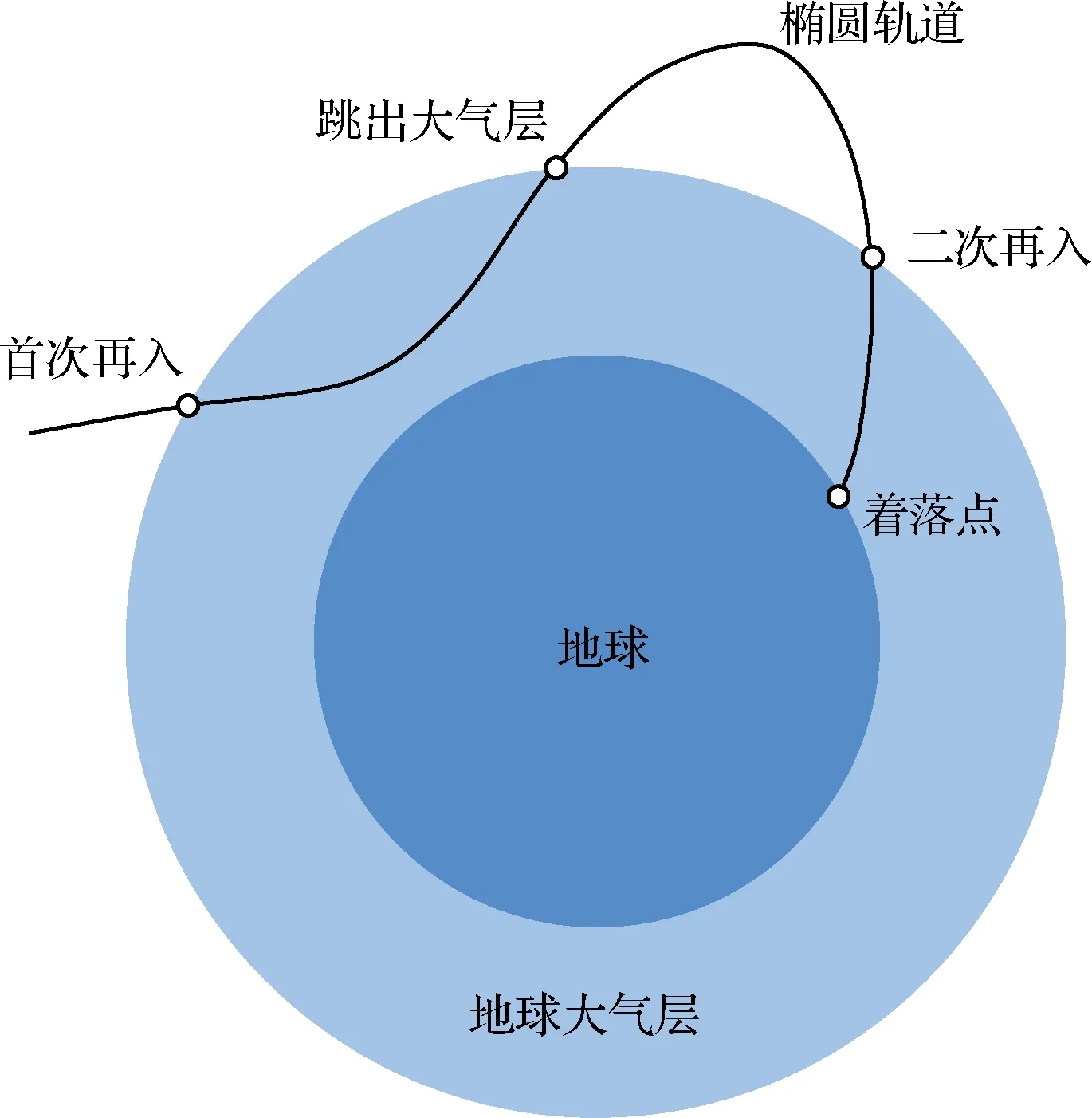
图1 跳跃式再入示意图

再入轨迹优化对于探月返回飞行器总体设计和制导控制系统设计具有重要意义[3-4]。与常规轨迹优化问题相比，跳跃式再入轨迹优化问题的特殊之处是首次再入段的微小轨迹误差会在跳出大气层的惯性飞行段被放大，进而给二次再入段轨迹带来比较大的偏差。这种二次再入段对首次再入段误差的高度敏感特性给轨迹优化带来了挑战。目前的方法为了简化，对首次再入段和二次再入段分开优化[5-6]，但是这种解耦处理方法难以保证轨迹的整体最优性。文献[7]采用高斯伪谱法对探月飞船跳跃式再入轨迹的可达域进行了分析，但是没有研究轨迹优化结果与数值积分结果的误差。此外，还有一些文献从设计的角度对跳跃式再入轨迹的相关参数影响规律[8]和能量管理方法[9]等进行了研究，但是这些方法不能充分挖掘跳跃式再入轨迹的性能。

跳跃式再入轨迹优化问题本质上属于最优控制问题，其求解方法主要分为间接法和直接法[10]。间接法借助变分法或者最大值原理，把泛函优化问题转化为两点边值问题求解；直接法通过对控制变量和/或状态变量进行离散把泛函优化转化为非线性规划(Nonlinear programming, NLP)问题，然后采用各种非线性规划算法求解，比如基于序列二次规划(Sequential quadratic programming，SQP)算法的SNOPT[11]和基于内点法的IPOPT[12]。直接法中的配点法[10]由于不需要推导最优性必要条件，并且对初值的敏感性较低，容易收敛，近年来得到广泛研究和应用。此外，研究还表明，将配点法与网格细化技术相结合，能够进一步提高配点法对复杂轨迹优化问题的适应能力[13-17]。这种方法的原理是应用网格细化技术在优化过程中根据轨迹的特点动态调整离散节点分布，从而采用较少的离散节点达到较高的优化精度，降低了配点法的计算量。以文献[17]为例，该研究基于稀疏配点法和网格细化技术对近地轨道返回的高超声速滑翔再入轨迹进行了优化，研究结果表明所述方法能够快速优化出一条严格满足路径约束和端点约束的再入轨迹。与高超声速滑翔再入轨迹不同，探月返回飞行器的再入返回轨迹具有跳跃特性并且由于二次再入轨迹对首次再入段的误差非常敏感，给轨迹优化带来挑战。

本文在节点自适应稀疏配点法的基础上，给出跳跃式再入轨迹的一种高精度优化方法，以探月飞行器跳跃式再入返回轨迹为例，通过数值仿真检验了所建立的轨迹优化方法的有效性。

1 跳跃式再入轨迹优化问题

1.1 再入轨迹运动模型

将飞行器简化为质点，那么描述飞行器质心运动的微分方程组为(忽略地球自转影响)[10]

(1)

式中：r，θ，φ分别为飞行器在地心赤道坐标系的矢径、经度、纬度；v，ψ，γ分别为飞行器的速度、航向角和航迹角；g为重力加速度，g=μ/r2，μ为地球引力常数，μ=3.98603195×1014m3/s2。

空气动力产生的加速度的沿飞行轨迹切向、法向和侧向的三个分量as，an，aw分别为

式中：σ为速度倾侧角，m为飞行器的质量。

升力和阻力的表达式分别为

式中：ρ为大气密度，A为气动参考面积，CL和CD分别为飞行器的升力系数和阻力系数。

1.2 再入初始条件

再入轨迹优化问题的初始条件如下

(2)

式中：t0为初始时刻；h为飞行高度，h=r-Re，Re为地球半径，Re= 6371.20 km；r0，θ0，φ0，v0，ψ0和γ0分别为相应的状态变量的初值。

1.3 路径约束

再入轨迹优化问题的控制变量为速度倾侧角，即u=σ(t)，其变化范围受到如下限制

σmin≤σ(t)≤σmax

(3)

式中：σmin和σmax为速度倾侧角的边界。

飞行器再入返回过程的过载直接关系到宇航员的生命安全和舒适度，需要对过载进行限制

(4)

式中：nmax为再入过程允许的最大过载。

为了使得飞行器安全返回，需要对高超声速再入过程的对流气动加热进行限制，即

(5)

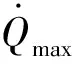
此外，考虑到飞行器结构的承受能力，还需要对再入过程的动压进行限制，即

(6)

式中：qmax为再入过程允许的动压上限。

1.4 末端约束

当飞行器的速度降至预定速度时，阻力降落伞打开，飞行器进一步减速下降。为了安全着陆，还需要对开伞时的飞行高度进行约束。综上所述，再入飞行器轨迹优化问题的终端约束条件为

v(tf)=vf,h(tf)≥hf, min

(7)

式中：tf为再入轨迹的终端时刻，vf为开伞时飞行器的速度，hf, min允许的最低开伞高度。

1.5 目标函数

轨迹优化的目标函数可根据实际设计需求选取。最大横向航程是衡量飞行器再入机动能力的重要指标。本文选取最大横向航程作为优化指标。由于φ0= 0°，ψ0= 0°，因而目标函数可写为

J=minφ(tf)

(8)

式中：φ(tf)<0，式(8)使横向航程最大化。

综上所述，跳跃式再入返回轨迹优化问题描述为：求解最优控制变量u(t)=σ(t)，使得目标函数最小化，并且满足再入动力学方程组(1)，初始条件(2)，轨迹路径约束(3)～(5)以及终端约束(7)。

2 跳跃式再入轨迹优化方法

2.1 自适应稀疏局部配点法

(9)

状态方程为

(10)

端点条件为

E(x(t0),t0,x(tf),tf)=0

(11)

路径约束为

C(x(t),u(t),t)≤0,t∈[t0,tf]

(12)

本文采用局部配点法求解轨迹优化问题。首先利用积分变换τ=(t-t0)/(tf-t0)将轨迹优化问题(方程(9)～(12))的时间区间变换至归一化的时间区间τ∈[0, 1]。假设单位区间[0, 1]上的N个离散节点为

G={τi:τi∈[0,1],i=0,1,…,N;τ0=0,τN=τf=1;τi<τi+1,i=0,1, …,N-1}

(13)

式中：τi称为离散节点或网格节点，τi在[0, 1]上可以均匀分布，也可以非均匀分布。

记xi=x(τi)，ui=u(τi)，对于状态方程(10)，基于q阶Runge-Kutta(RK)方法的离散格式为

(14)

式中：Δt=tf-t0，hi=τi+1-τi，fij=f(xij,uij,τij；t0,tf)，xij，uij和τij为中间变量，xij由下式给出

(15)

式中：τij=τi+hiρj，uij=u(τij)，ρj,βj,αjl均为已知常数并且满足0≤ρ1≤…≤ρq≤1。当αjl= 0(l≥j)时，为显式格式，否则为隐式格式。采用类似的方法，可将目标函数离散化。常用的离散格式有梯形格式(q= 2)，Hermite-Simpson格式(q= 3，简记为HS格式)，经典四阶Runge-Kutta格式(q= 4)等。

(16)

并且满足如下约束

(17)

Ci=C(xi,ui,τi;t0,tf)≤0

(18)

(19)

E(x0,t0,xf,tf)=0

(20)

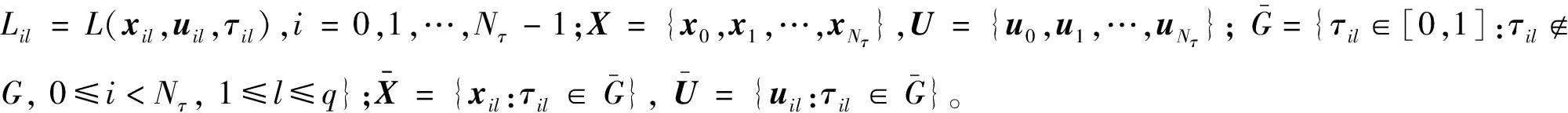
本研究采用HS格式，该格式需要用到区间中点的变量和函数值，为此将区间中点的控制量也作为优化变量并且在区间中点添加路径约束，即

(21)

(22)

约束条件为

(23)

Ci=C(xi,ui,τi;t0,tf)≤0

(24)

(25)

E(x0,t0,xf,tf)=0

(26)

其中

在数值优化时，为了使轨迹优化问题具有实际物理意义，还需要添加时间差约束

Δt=tf-t0>0

(27)

求解方程(22)～(27)所示的NLP问题即可得到轨迹优化问题的最优解。本文采用美国斯坦福大学基于SQP算法开发的SNOPT[11]求解NLP问题。

为了提高轨迹优化的求解效率和精度，本文应用稀疏差分算法[18]提高NLP偏导数的计算效率，应用节点细化技术[19]动态调整离散节点分布，提高对跳跃式再入轨迹的适应能力。在采用SNOPT求解NLP时，为SNOPT提供NLP的一阶偏导数矩阵(即雅克比矩阵，定义为目标函数和全部约束对全部自变量的偏导数矩阵)能够显著提高优化的计算效率，但是偏导数矩阵的计算量比较大。稀疏差分法[18]通过分析偏导数矩阵的稀疏特性，将其中的占绝大多数的零元素识别出来，并且将其中的非零元素的值通过矩阵链式求导运算分解为原始轨迹优化问题的偏导数，然后采用稀疏差分方法计算，从而大幅度减小偏导数的计算量。节点细化技术[19]的原理是数据压缩，每次优化出一条轨迹之后，根据轨迹的变化特性，在光滑区域对离散节点进行压缩，减少节点数量，在非光滑区域插入一些新节点，使之分布更密，然后再次优化轨迹，综合效果是采用较少的离散节点高精度描述轨迹。稀疏差分法和节点细化技术都具有很强的通用性和鲁棒性，对于本文的优化问题，只需要设置用于判断轨迹是否光滑的阈值参数即可(判断每个节点处的控制量与采用其周围节点的插值结果的差异是否超过阈值，若超过，则认为轨迹不光滑，否则认为轨迹光滑)。

2.2 跳跃式再入轨迹优化方法

对于跳跃式再入轨迹，由于二次再入段对首次再入段的误差非常敏感，若将首次再入段和二次再入段作为整体进行优化会导致二次再入轨迹的优化精度较低。本文在自适应稀疏局部配点法的基础上，提出一种能够高精度求解跳跃式再入轨迹优化问题的方法。该方法的关键之处是从跳跃轨迹的最高点开始，对二次再入轨迹进行重新优化。如图2所示，首先，将跳跃式再入轨迹作为整体进行优化，得到最优倾侧角随时间变化曲线；然后，按照最优倾侧角积分再入动力学方程组得到最优轨迹；当积分至跳跃轨迹的最高点时，以实际积分得到的状态变量作为新的初始条件(其它条件保持不变)，对二次再入轨迹重新优化，求解新的最优倾侧角。考虑到优化计算需要耗费一些时间，为了使得方法在制导跟踪领域具有实用性，本文方法在解出二次优化问题的最优倾侧角之前，仍然采用整体优化得到的最优倾侧角作为二次再入轨迹的控制输入。因为在跳跃轨迹的最高点附近大气非常稀薄，气动力对轨迹的影响非常小，所以这样近似处理是合理的。

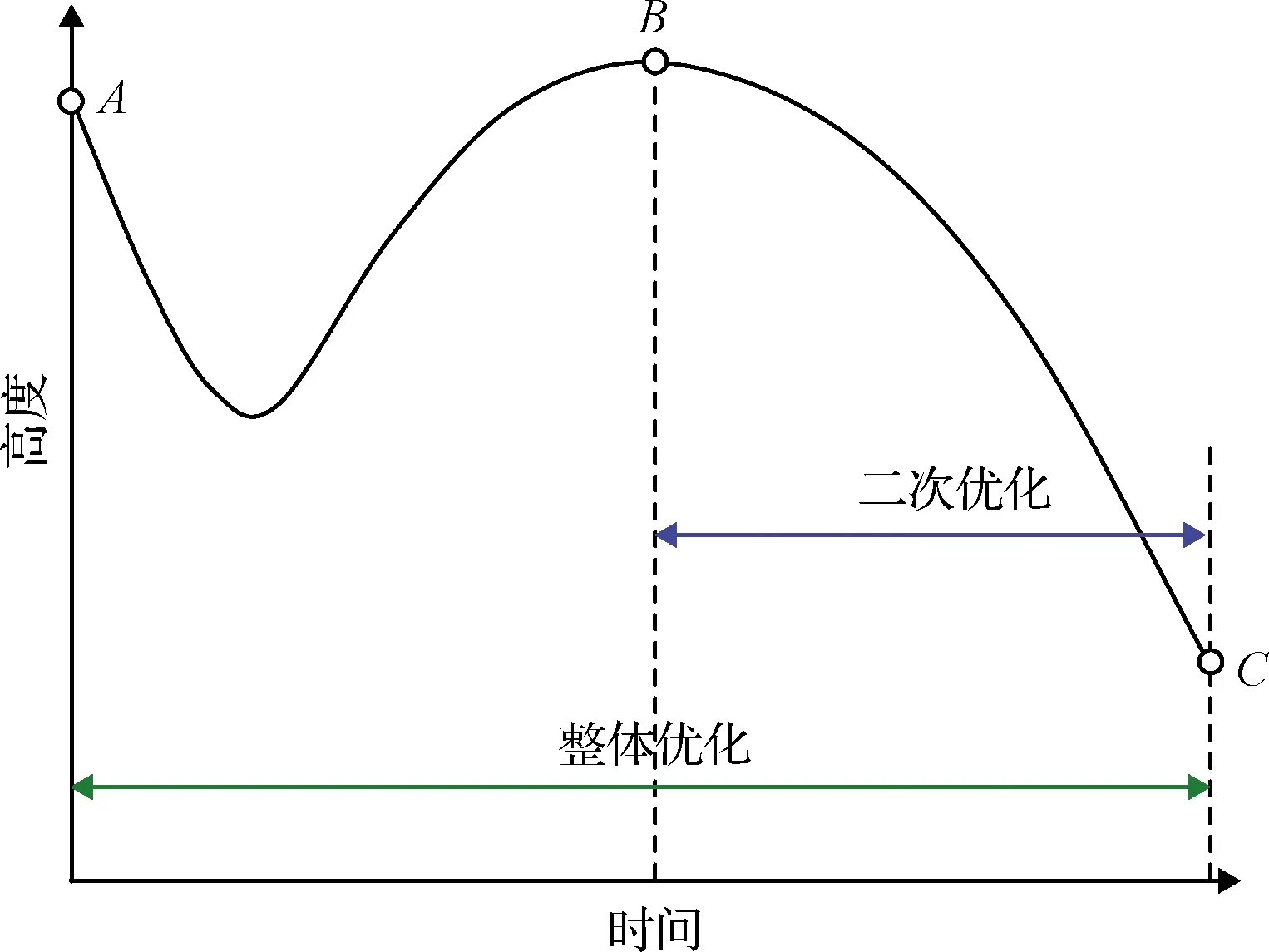
图2 跳跃式再入轨迹优化策略

本文方法的具体流程如下：

1)应用基于稀疏差分法和节点自适应细化技术的局部配点法求解由方程(1)～(8)描述的跳跃式再入轨迹优化问题，得到最优倾侧角σ1(t)。

2)以σ1(t)为控制变量，采用四阶Runge-Kutta方法积分由方程组(1)～(2)描述的微分方程组初值问题至跳跃轨迹的最高点(即最大高度处)，得到最高点的状态变量x1,f以及对应的时刻t1,f。

3)以t1,f和x1,f作为新的初始条件，对由方程组(1)和(3)～(8)描述的再入轨迹优化问题进行重新优化(即二次优化)，得到新的最优倾侧角σ2(t)和终端时刻t2,f，记下二次优化的耗时为Δt2。

4)从跳跃轨迹的最高点开始，以x1,f为初始条件，以σ1(t)为控制变量，继续积分再入动力学方程组(1)至t2,1=t1,f+ Δt2，得到状态变量x2,1。

5)以t2,1和x2,1为初始条件，以σ2(t)为控制变量，积分再入动力学方程组(1)至终端时刻t2,f。

6)将在步骤2)、4)和5)中积分得到的三段轨迹(含各段采用的控制变量)组合在一起，即可得到最优跳跃式再入轨迹和相应的控制变量。

相对于间接法和直接打靶法等其它方法，配点法的优势之一是对优化初值的敏感性较低。尽管如此，良好的优化初值仍然有利于加速轨迹优化的收敛。本文在对跳跃式再入轨迹进行第一次优化时，状态变量的优化初值选取初始状态变量和终端状态变量的连线(对于终端状态给定的变量)或者初值状态变量常值(对于终端状态没有给定的变量)，控制变量的优化初值取σ(t)=-45°。在后续的节点细化以及二次优化时，均利用前一步得到的最优轨迹通过插值提供较为准确的优化初值。

3 仿真结果

3.1 方法1(整体优化)

为了对比，本文首先不考虑二次优化，在整个时间区间对跳跃式再入轨迹进行优化。采用本文3.1节介绍的自适应稀疏局部配点法求解该问题。图3为优化出的最优控制变量随时间变化曲线。图4为优化出的最优高度和速度随时间变化曲线。图3和图4中的圆圈表示离散最优解(总共采用142个非均匀分布的离散节点)。图3中的细实线为对离散控制变量进行插值得到的连续控制变量随时间变化曲线。图4中的细实线为根据图3所示的最优控制变量采用四阶Runge-Kutta数值积分方法对再入动力学方程组进行数值积分得到的结果。

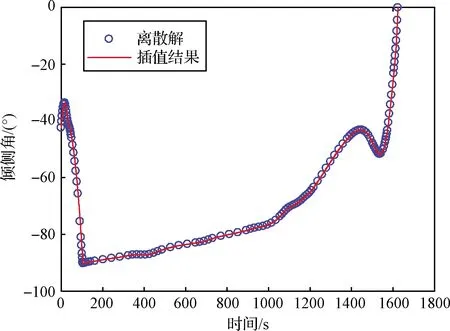
图3 最优倾侧角变化曲线(方法1)

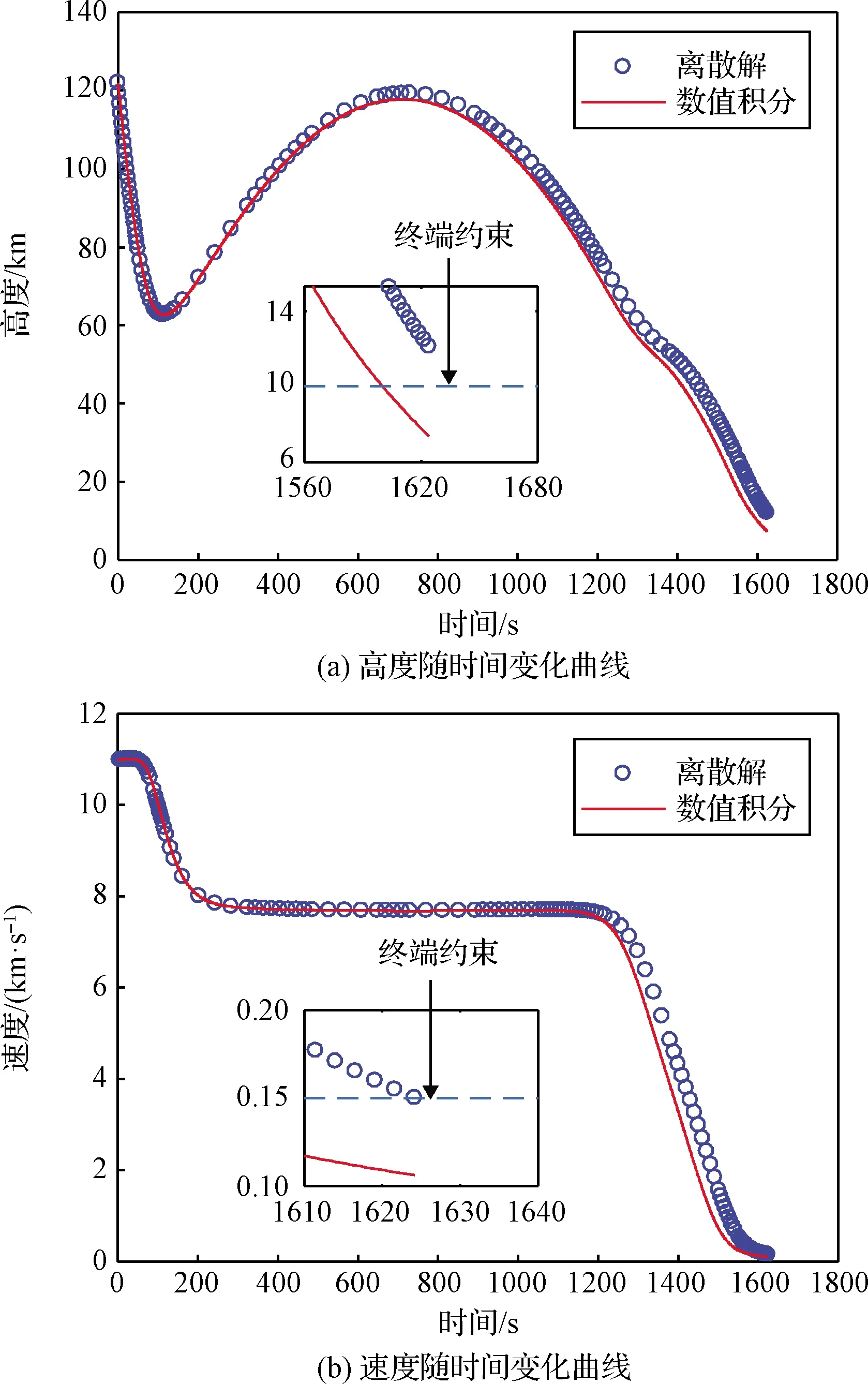
图4 最优高度和速度变化曲线(方法1)

由图4可知，在初次再入阶段，数值积分结果与离散最优解的差异微小，但是从飞行器跳跃出大气层开始，数值积分结果与离散最优解逐渐出现了明显的差异。在轨迹终端，数值积分得到的终端高度为7361.8 m，终端速度为106.1 m/s，均不满足开伞条件。数值积分结果与离散最优解的高度差异高达-4768.3 m，速度差异高达-43.9 m/s，显然超出了合理范围。这种差异主要是因为在初次再入段，数值积分结果与离散最优解存在微小的误差(由于数值离散造成的，不可避免)，而跳跃式再入轨迹的跳跃段和二次再入段对首次再入段的误差非常敏感，使得首次再入段的误差沿轨迹累积并传播，最终导致轨迹的终端误差过大。对于常规轨迹优化问题，数值积分结果与离散最优解也存在误差，只是误差通常非常小，其影响可以忽略不计。理论上，增加离散节点的数量能够减小这种误差，但是实际上如果离散节点数量过多，NLP的规模过大，优化算法的收敛性通常会变差，甚至无法收敛[21]。

3.2 方法2(整体优化+二次优化)

为了解决数值积分结果和离散最优解差异过大问题，本文在跳跃式再入轨迹整体优化结果的基础上，从跳跃的最高点(对应的时间t1,f=711.2 s)开始，对二次再入轨迹重新优化，具体方法参见2.2节。图5给出优化的控制变量随时间变化曲线，图6给出优化的高度和速度随时间变化曲线。其中，跳跃最高点之前的轨迹是通过对再入轨迹整体优化得到(参见2.1节)，跳跃最高点之后的轨迹为二次优化的结果(本文考虑了二次优化的耗时，因而连接点相对最高点略微右移)。图5和图6中的圆圈表示二次优化得到的离散最优解(采用84个非均匀分布的节点)。图5中的细实线是对离散控制变量进行插值得到的连续控制变量随时间变化曲线，图6中的细实线是根据图5所示的最优控制变量对再入动力学方程组进行数值积分得到的结果。

对比图5和前述图3可知，对完整再入轨迹优化和对二次再入轨迹重新优化得到的二次再入控制变量差别不大。对比图6和图4可知，引入二次优化之后，二次再入轨迹的数值积分结果与离散最优解非常接近，终端高度误差仅为2.12218 m，终端速度误差仅为0.02580 m/s，很好地满足了再入飞行器的开伞条件约束。可见，通过对二次再入段重新优化显著提高了跳跃式再入轨迹的优化精度。

图5 最优控倾侧角变化曲线(方法2)

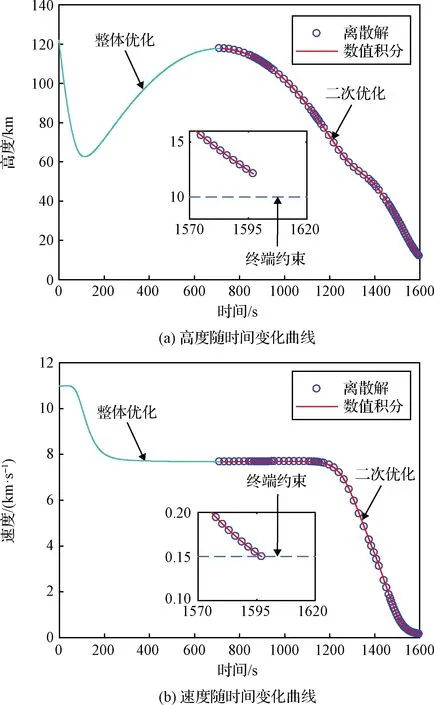
图6 最优高度和速度变化曲线(方法2)

图7给出优化的三维再入轨迹，其中圆圈为离散最优解，细实线为数值积分结果。为了便于展示轨迹特征，图7中还给出了飞行器在地球表面投影点的轨迹。可见，为了取得最大横向航程，飞行器在首次再入过程中利用气动力改变速度方向进行转弯，在二次再入过程中进一步利用气动力进行横向机动。图8给出再入过程中过载等路径约束沿轨迹变化曲线。可见，最优轨迹的过载、热流和动压都满足路径约束要求，其中过载在首次再入段的最低点附近达到上限，其它约束均未达到上限。

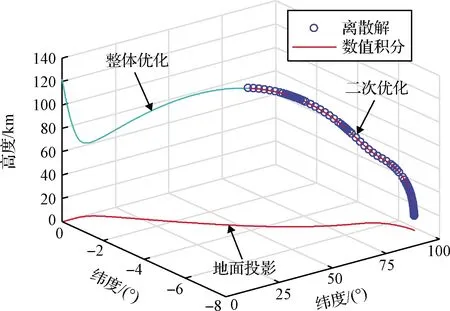
图7 三维最优跳跃式再入轨迹(方法2)

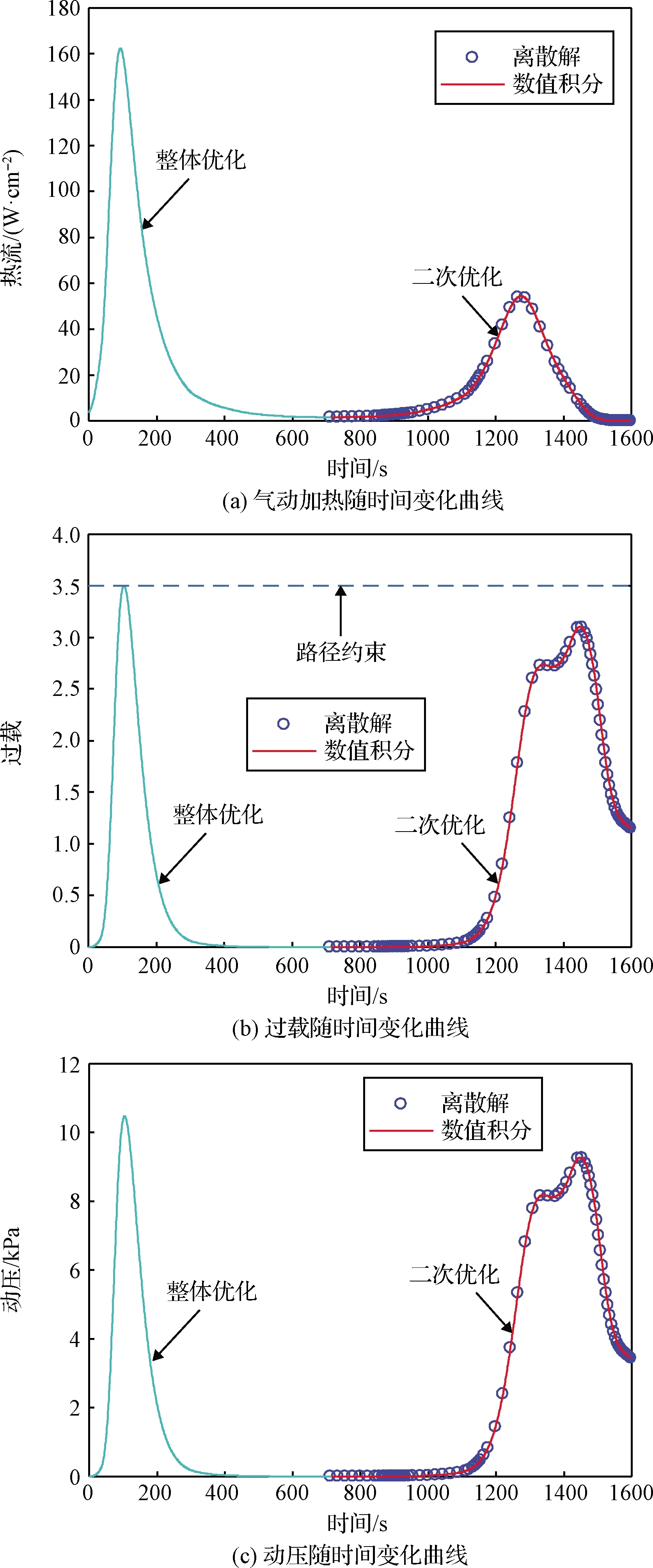
图8 最优轨迹的路径约束(方法2)

表1给出方法1(整体优化)和方法2(整体优化+二次优化)的优化结果对比。对于方法2，表中还给出了不同的二次优化耗时Δt2对数值积分终端误差的影响。从表1中可以看出，通过对二次再入轨迹重新优化，可以将终端时刻的速度误差和高度误差降低3～4个数量级，从而使得飞行器的开伞条件得到严格满足。在目标函数方面，两种方法解出的最大横向航程几乎没有差别。需要强调的是，方法1的优化结果对应的数值积分终端误差过大、不满足开伞条件，实际上并不是可行轨迹。

在本算例中，二次再入轨迹重新优化消耗的时间为Δt2= 2.4 s。为了使方法具有实用性，本文在二次优化得到新的控制变量之前，仍然采用整体优化得到的控制变量作为输入对再入动力学方程组进行积分。虽然二次优化得出的控制变量和整体优化得出的控制变量存在差异，但是仿真结果表明这样处理对二次再入轨迹几乎没有影响。目前，国产宇航芯片的主频可达到300 MHz[22]，而本文采用的计算平台的处理器主频为1.6 GHz，考虑到内存和软件等性能的差异，预计宇航级计算机的计算性能与本文采用的计算平台相差10～20倍。进一步仿真研究表明，即使在计算能力较低的宇航级计算机上(以计算能力降低至1/20为例)，二次优化的耗时会显著增加，但是上述处理方式对二次再入轨迹仍然几乎没有影响，如表1所示。因为跳跃最高点的高度为117.8 km，大气非常稀薄，气动力非常小，因而在最高点附近采用不够准确的控制变量积分再入动力学方程组对轨迹几乎没有影响。因此，本文提出的处理方法使得二次再入轨迹的优化是一种准实时优化，在再入轨迹的制导领域具有应用潜力。

表1 不同方法的优化结果对比

4 结论

探月返回飞行器跳跃式再入返回轨迹优化问题是复杂的多约束、非线性最优控制问题，特别是二次再入轨迹对首次再入段的误差非常敏感，给优化带来挑战。本文提出一种高精度求解跳跃式再入轨迹优化问题的方法。该方法首先应用节点自适应稀疏配点法对完整跳跃式再入轨迹进行优化，然后根据优化得到的控制变量积分再入动力学方程组，当积分到跳跃轨迹的最高点时，以积分得到的状态变量值作为新的初始条件，对二次再入轨迹重新优化。在求解二次再入轨迹期间(约2～3 s)，继续基于整体优化解出的最优控制积分再入动力学方程组，直到优化算法重新优化出二次再入段的最优控制，然后根据新的最优控制积分再入动力学方程组至轨迹终端。仿真结果表明：与不采用二次优化的方法相比，采用二次优化能够将跳跃式再入轨迹的终端高度和速度误差降低3～4个数量级。此外，在跳跃的最高点附近进行的二次优化是一种准实时优化，在再入轨迹的精确制导领域具有应用潜力。