基于Workbench零件曲柄臂可靠性优化分析

2021-03-12张明松王恩恒肖锦志

南方农机 2021年5期

张明松，庄桥，王恩恒，肖锦志

（三峡大学机械与动力学院，湖北宜昌 443002）

文章以ANSYS的优化设计模块为优化工具，以曲柄臂加强筋的厚度1个参数为设计变量，对可调整曲柄臂在轴向载荷条件下结构参数进行了优化，通过优化获得了合理的设计参数，在保证结构强度和刚度的前提下，实现了减重设计的目标[1]。

1 产品轻量化设计现状

目前，对于产品轻量化设计方面，工程技术人员普遍采用有限元分析软件经静力学的求解后，基于其求解结果完成零部件的轻量化设计。以ANSYS软件为例，其具有强大的优化设计与可靠性设计功能，在ANSYS Workbench中对结构进行优化设计时主要运用设计探索优化(Design Exploration)和拓扑优化(Topology Optimization)两大模块里。其中探索优化模块主要用于产品的参数化优化，而拓扑优化模块因其对于产品结构的优化方面，具有求解操作简便且简化后的结构更加便于观察的特点，被广泛应用于结构的轻量化设计中。

2 曲柄臂结构的轻量化设计

2.1 基于有限元分析的优化设计

结构优化设计流程如图1所示。过程主要有前处理、求解参数和后处理等环节组成。首先必须对模型进行分析、建立参数化模型、定义模型的载荷和提取并声明设计变量。在此基础上选择优化方法，指定优化循环过程的控制方式，从而进行优化分析，分析结束后查看设计序列结果并进行后处理[2]。

图1 优化设计过程图

2.2 数学模型的建立

图2 曲柄臂加强筋厚度示意图

减轻曲柄臂的质量及降低曲柄臂所受应力为优化目标。约束条件即为结构最大应力为35MPa，主要取曲柄臂的加强筋厚度A作为主要设计的变量，曲柄臂加强筋厚度示意图如图2所示。

其轻量化优化设计的数学模型可以表示为[3]：

式中：m（D）为曲柄臂质量；σD为所受最大等效应力值；[σ]为其许用应力极限；D为优化变量。采用上述数学模型对曲柄臂进行优化计算。

2.3 曲柄臂静力学

为降低优化设计计算量，保证设计的安全性，因此必须考虑曲柄臂所适用环境中的典型恶劣载荷作用下的应力、应变情况。要准确计算结构的最大应力和应变，还必须确定在特定载荷作用下的最危险工作状态。

在有限元分析过程中，为减少计算量并提高网格划分质量，在建立有限元模型时，忽略机械臂上的倒角、倒圆。材料为结构钢，将机械臂左右两侧圆柱孔施加以圆柱支撑且释放切向自由度，对中间圆柱孔施加竖直向下的轴承载荷，大小为10 000N，材料为结构钢，泊松比为0.3，密度为7 850mg/m3，杨氏模量为200GPa，许用应力[σ]为35MPa。将曲柄臂的三维模型导入ANSYS Workbench后进行受力分析，在Mesh模块下定义模型网格形状为高阶六面体网格，为了便于后续拓扑优化结果的观察，曲柄臂采用自由网格划分法，共有5 703个单元和10 389个节点，得出曲柄臂受力分析图如图3所示。图3（a）曲柄臂受力位移变形小、图3（b）曲柄臂所受应力小的区域和图3（c）曲柄臂在疲劳分析中安全因素很大，具有很大的轻量化优化空间。

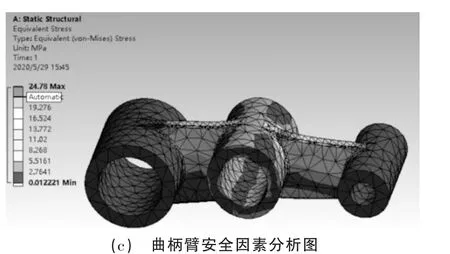
图3 曲柄臂受力分析图

2.4 优化过程及结果

采用ANSYS Workbench软件的优化方法，在对有限元模型施加载荷与约束的基础上，利用ANSYS Workbench中的拓扑优化(Topology Optimization)模块，判断当前最大应力、应变是否超过设计变量的初始赋值。并不断修改初始参数赋值，进行多次优化处理，直到满足优化条件为止。并在完成初始状态的有限元分析计算后，在ANSYS Workbench建立与分析文件中变量相对应的参数，并进入优化设计模块指定分析文件，选择优化工具，对轴向载荷作用下的最危险支撑状况进行循环优化分析直到满足循环终止条件，得到设计变量的优化结果。在满足约束条件和目标函数[4]的基础上得到的设计变量优化结果与初始值比较[5]，如表1所示。

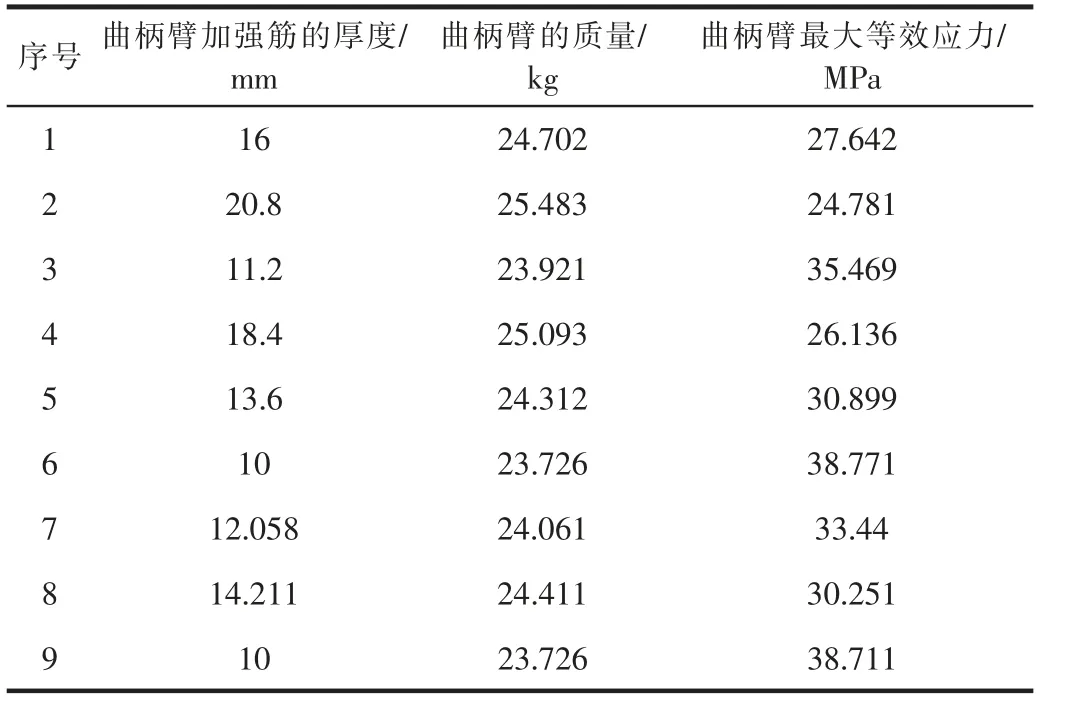
表1 曲柄臂加强筋厚度数值模拟参数

3 曲柄臂静力分析结果

由表2和图4可知，在结构参数进行优化调整后，曲柄臂质量减轻了4.1%，实现了局部轻量化，且其最大等效应力为30.899MPa，比优化前下降了4.101MPa，低于其许用应力。这一优化既节省了机器人的能耗，又提高了其结构强度，同时基于零件疲劳分析得出零件的最小安全因素至少为2.806 3，由此可以得出结论：优化减重后最小安全因素并不是随着最大等效应力减小而增大，在机械零件减重优化后需要对优化后的模型进行疲劳分析验证，通过这种优化设计后的曲柄臂，能够满足工程上的使用要求[6]。