例谈增根的产生与作用

苏凡文

(山东省宁阳县第一中学 271400)

中学阶段，增根是学生普遍感觉比较棘手的问题．增根是指方程求解后得到的不满足题设条件的根．了解增根产生的原因，对根进行合理取舍，是中学生必备的数学素养．本文以高考题目为例谈一下增根问题．

一、增根产生的原因

增根的产生源于题目条件转化为结论的过程中，使得条件成为结论的充分不必要条件．如果在题目的解答过程中将条件等价转换为结论，增根自然会被舍去．

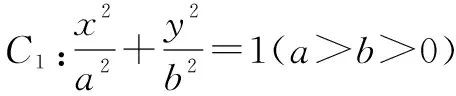
(1)求C1的离心率；

(2)设M是C1与C2的公共点，若|MF|=5，求C1与C2的标准方程．

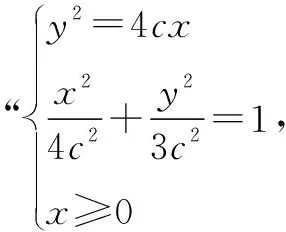
我们常常说，二元二次曲线方程联立在实数范围内容易产生增根，但两圆联立不产生增根，这是为什么呢？

二、探索两圆联立不产生增根的原因

①当两圆相交时，显然根轴为公共弦所在的直线，根轴与两圆的两个公共点即是两圆的两个公共点；

②当两圆外切时，两圆的1个公共点在根轴上，且d=r1+r2．

下面证明根轴与两圆只有一个公共点．

所以，两圆外切时，两圆的1个公共点即根轴与两圆的1个公共点；

③当两圆内切时，两圆的1个公共点在根轴上，设r2

所以，两圆内切时，两圆的1个公共点即根轴与两圆的1个公共点；

所以，两圆内含时，两圆无公共点，根轴与两圆也没有公共点．

所以，两圆外切时，两圆无公共点，根轴与两圆也没有公共点．

综上所知，“圆与圆的公共点的个数”和“根轴与圆的公共点个数”是相同的．

所以，两圆的位置关系本质是根轴与圆的位置关系，因为直线与二次曲线联立不会出现增根，故两圆联立不会出现增根．

三、增根在部分题目中存在的意义

很多人认为增根本身没有存在的必要性和价值性，是严谨数学的一个瑕疵，这其实是不对的，细细研磨会发现，增根在部分题目中对解题有些积极的提示性作用．

(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

分析本题绝大部分学生得6分或者7分，主要原因是计算到4k2+8km+3m2-2m-1=0不会因式分解，若利用变换主元法，可得4k2+8mk+(m-1)(3m+1)=(2k+m-1)(2k+3m+1)．但是这种二元二次方程因式分解绝大部分学生不会做．下面提供一种利用增根进行因式分解的方法．