数学语言转换在集合中的应用

杨伟达

(广东省广州市花都区第二中学 510800)

众所周知，数学语言分为文字语言、图形语言、符号语言.其中文字语言通俗易懂，图形语言直观形象，符号语言简洁抽象，各有所长，相互渗透.而集合作为现代数学的基本语言，简洁、准确地表述数学内容，在符号语言、图形语言、文字语言之间寻求转换，实现代数与几何之间的相互转化，使学生深刻地体会数学的本质，进而更好地提高学生的数学素养．

一、文字语言与图形语言之间的转换——由准确到直观

将文字语言抽象出来进行符号化，借助数学语言之间的转换获取信息，以图释译，直观形象．寻找集合语言之间的转译，就是把问题中的文字语言转译为图形语言，从而达到快速解题．

例150个学生当中会讲英语的有36人，会讲日语有20人，既不会讲英语又不会讲日语的有8人，既会讲英语又会讲日语的认数为( ).

A.20个 B.14人 C.12人 D.10

分析本题用文字准确描述数学问题，不少学生无从下手．若把文字语言转换成图形语言，用韦恩图表示出来，问题即可迎刃而解．

解设50个学生为全集U，会讲英语的学生为A，会讲日语的学生为B，则既不会讲英语又不会讲日语的同学为(CuA)∩(CuB)，既会讲英语又会讲日语的同学为A∩B．

所以card(A)=36，card(B)=20，card(U)=50，card((CuA)∩(CuB))=8

即card(A∩B)=card(A)+card(B)+card((CuA)∩(CuB))-card(U)=14

故选B．

二、描述法与图形语言之间的转换——由抽象到直观

对数学语言的把握就是把符号化的数学知识转译成通俗易懂或者直观形象的图形语言．

描述法表示集合，符号化的语言简洁、抽象，在解决问题时，往往难于突破，此时借助图形的直观，问题就会事半功倍的效果．

例2 若集合A={x|2a+1≤x≤3a-5}，B={x|5≤x≤16}，则能使A⊆B成立的所有a组成的集合为( ).

A．{a|2≤a≤7} B. {a|6≤a≤7}

C. {a|a≤7} D.φ

分析本题考查了含参集合的子集.涉及不等式时常常用数轴表示，在动集合与定集合的相互关系中进行分类讨论，通过图形的直观列出不等关系式，解不等式即可将问题解决．

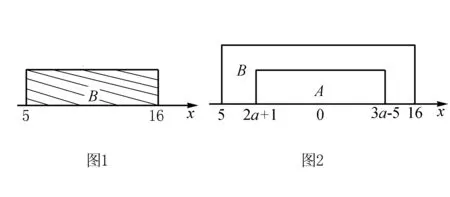
解(1)当2a+1>3a-5时即a<6，此时A=φ，显然满足条件A⊆B；

(2)当2a+1≤3a-5时即a≥6，此时A≠φ，则有

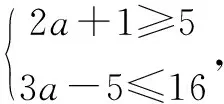
综上所述，由(1)(2)可得a≤7，所以选C．

三、描述法与列举法之间的转换——由抽象到具体

集合中的描述法与列举法之间的转换，就是通过符号语言所呈现的数学信息，并把这些信息同已有的数学知识相联系，分析出符号语言所表达的含义，将它一一列举，从而达到解决问题．

例3 已知A={x|x2+3x-4=0}，B={x|x2-ax+a-1=0}，若B⊆A，则a的值为____．

分析本题涉及子集运算及方程的求解．首先将集合A、B化简，描述法转化列举法，再进行分类讨论即可将问题解决．

解A={x|x2+3x-4=0}={1,-4}

(1)当a=2，则B={x|x2-ax+a-1=0}={1}，显然满足条件B⊆A

(2)当a≠2，则B={x|x2-ax+a-1=0}={1,a-1}，当a-1=-4时即a=-3，此时A=B也满足B⊆A．

综上所述，a=2或a=-3．

四、描述法与描述法之间的转换——由抽象到直观

集合语言简洁、抽象，至美至简！在解决有关集合问题时，化抽象为具体，寻求更加具体、明确的等价条件，更加直观、明了的数学知识，往往需要对描述法进行再转述，问题就会豁然开朗．

例4(2020·新课标Ⅰ·2)设集合A={x|x2-4≤0}，B={x|2x+a≤0}，且A∩B={x|-2≤x≤1}，则a=( ).

A．-4 B．-2

C．2 D．4

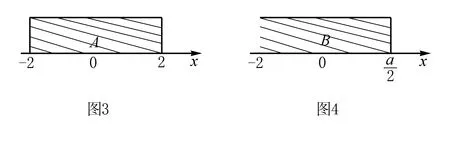
分析本题考查集合的交集运算及不等式的解法．在涉及一元二次不等式和一元一次不等式的解法，通常化简集合A，B，画出数轴，再由交集的定义及韦恩图，可得a的方程，解方程即可．

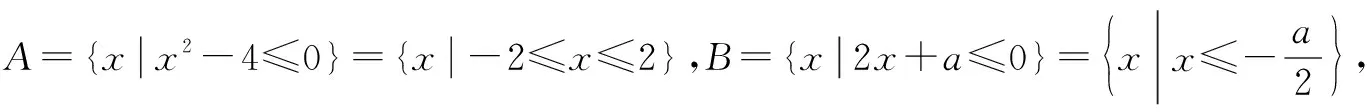
故选B．

点评常规命题思路是已知两个集合求交集运算．而命题专家这次拚弃传统，逆向而行，知道交集求某一集合，这不愧是一种创新．

总之，学习数学的过程就是发展数学能力的过程，也就是数学素养培养和构建的过程.在集合的教与学中，教师要善于引导学生在这三种语言之间进行的切换、转译，从而达到重新认识，获得新知，进而达到快速、有效的解决问题．