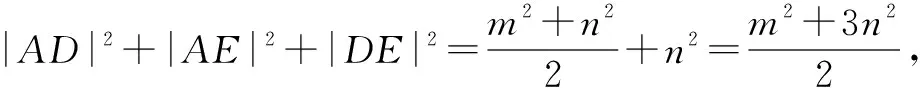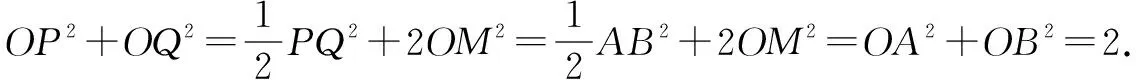中线长定理的证明及应用举例

李秀元

(湖北省武穴市实验高级中学 435400)

一、中线长定理的内容、地位及证明

中线长定理，又称阿波罗尼奥斯定理，是关于三角形三边和中线长度关系的欧氏几何定理.文字表述为：三角形一条中线两侧所对边的平方和等于底边一半的平方与该边中线的平方和的2倍.

图1

如图示，设△ABC的三边分别为a，b，c，边BC，AC，AB上的中线分别记为ma，mb，mc，则：

中线长定理在人教课标教材A版中一共出现三次，一次是《数学》必修5第一章《解三角形》20页习题13，作为余弦定理的应用，它突出了中线长的计算：

△ABC的三边分别为a，b，c，边BC，CA，AB上的中线分别记为ma，mb，mc，应用余弦定理证明：

一次是《数学》必修2第三章《直线与方程》110页B组习题7，以解析法的形式，突出了中线长与三角形三边的关系：

已知AO是△ABC边BC的中线，求证：

|AB|2+|AC|2=2(|AO|2+|OC|2).

第三次是《数学》必修2第三章《直线与方程》105页例4在两点间距离公式的应用基础上，给出了平行四边形的性质，也可以理解为中线长定理的变形式：

证明平行四边形四条边的平方和等于两条对角线的平方和.

下面用不同方法证明如下：

证法1应用余弦定理(只证第一式，其余同理).

证法2综合应用平面向量知识和余弦定理.

证法3解析法.

如图，以BC边的中点为原点，边BC所在直线为x轴建立直角坐标系.

图2

设C(c,0)，A(a,b)，则B(-c,0).

|AB|2=(a+c)2+b2；|AC|2=(a-c)2+b2；|OA|2=a2+b2；|OC|2=c2.

所以，|AB|2+|AC|2=(a+c)2+b2+(a-c)2+b2=2(a2+b2+c2)，

2(|AO|2+|OC|2)=2(a2+b2+c2).

因此，|AB|2+|AC|2=2(|AO|2+|OC|2).

二、中线定理的简单应用

例1Rt△ABC中，斜边BC为m，以BC的中点O为圆心，作直径为n(n

图3

A. 2 B. 4 C. 5 D. 10

图4

在△PAB中，应用中线定理，有2(|PA|2+|PB|2)-|AB|2=4|PD|2，故2(|PA|2+|PB|2)=|AB|2+4|PD|2=20|PC|2，选D.

说明以上两题建系求解一样可行，而应用中线长定理则是不错的选择.

图5

说明本题作为13年高考重庆卷的选择压轴题，有其把关和选拔功能，是一道难题.虽然有垂直关系，有长度，可以建系求解，但计算麻烦，短时间内会逼得学生放弃.应用中线长定理直接将目标和已知条件联系在一起，解题干净利落，值得欣赏.

例4 已知P(a,b)为圆x2+y2=1内一个定点.作直线PA⊥PB，分别交圆于A，B.以A，P，B为三个顶点作矩形，求矩形的第四个顶点Q的轨迹.

图6

例5 已知m，n是两个非零向量，且|m|=1，|m+2n|=3，则|m+n|+|n|的最大值为( ).

图7

说明本题的综合较强，考查了向量的加减法，向量模的几何意义，中线长定理，以及基本不等式等知识，难度较大.