强化问题逻辑 引领解题方向

郑 良

(安徽省合肥市第四中学 230000)

解题过程就是实现从条件到结论的通达.教学中发现部分学生弄不清条件与结论的逻辑关系，常常在解题过程中出现不等价变形而不自知等等.如何避免逻辑关系的颠倒，实现问题的等价转化？学生们不仅要有坚实的基础知识、熟练的基本技能，必要的解题经验，还要具备通过阅读理解题意、结合问题制定解题方案、根据困难所在调整思维方式、反思比较中优化方法的能力.下面给出四道例题并对其关键点进行点评，以期能对大家有所帮助.

例1 四边形边框顶点分别为A、B、C、D，一蚂蚁沿折线BCDA由点B向点A运动，蚂蚁位置P与AB构成△ABP的面积为S，老师在黑板上画出S=f(x)的图像如图1所示，同学甲、乙、丙、丁分别做出如下判断：

甲：边框ABCD是平行四边形；

乙：边框ABCD是等腰梯形；

丙：当蚂蚁到AD中点时，△ABP的面积是10；

丁：路程x∈[10,14]时，S=f(x)=56-4x.

试问哪些同学的判断是正确的？

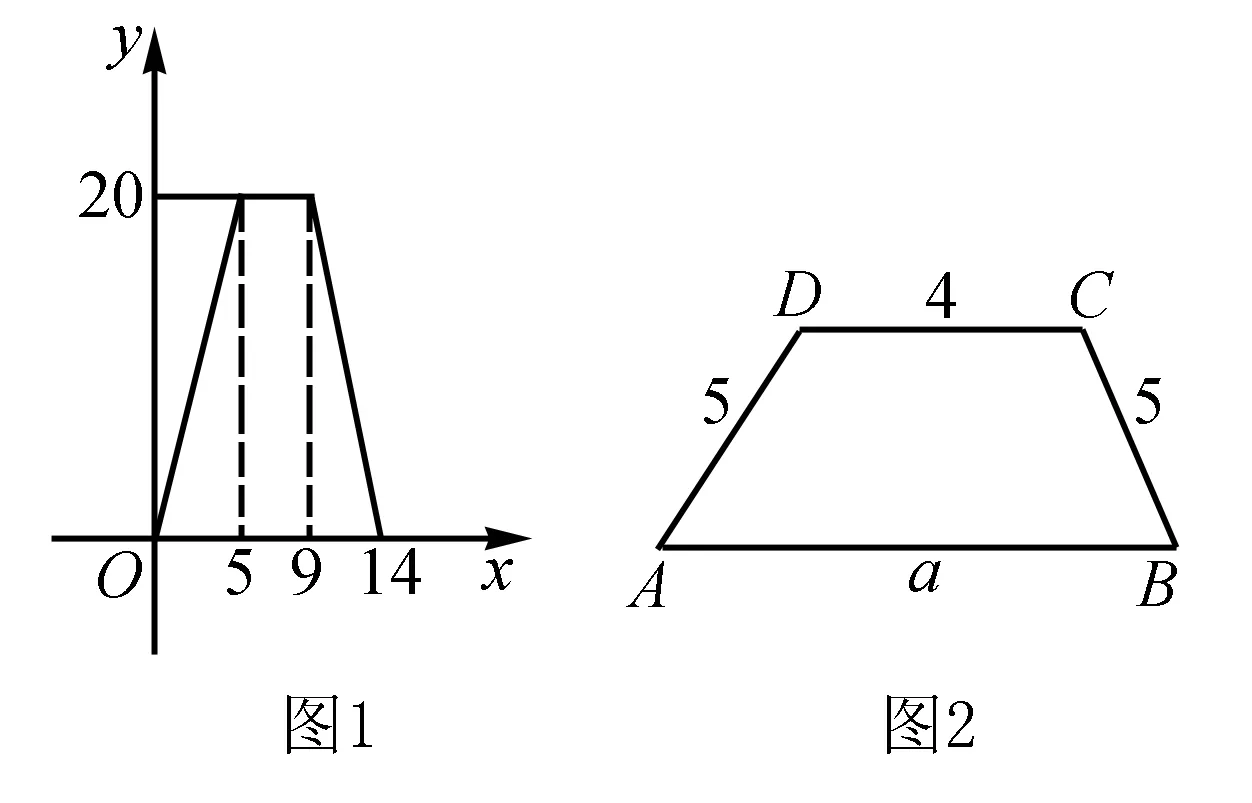
解当x∈[5,9]时，从图1可知△ABP的面积不变，此时S△ABP=20，则四边形ABCD中必有两边AB与CD平行，且CD=4，BC=5，DA=5.

如图2所示，若ABCD是平行四边形，则S△ABP的最大值只能为10，达不到20.所以乙、丙、丁的回答是正确的.

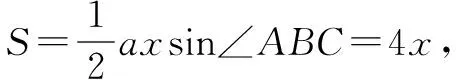
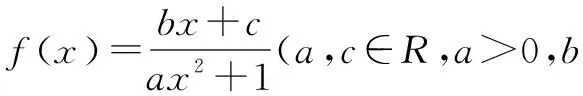
(1)试求函数f(x)的解析式；

(2)是否存在直线L与y=f(x)的图像只交于点P,Q两点，并且使得P,Q的中点坐标为(1,0)？若存在，求出直线L的方程；若不存在，请说明理由.

解(1)由f(x)是奇函数，易知c=0；

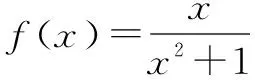
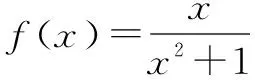
因此，直线L与函数f(x)的图像共有三个交点，与“只交于两点”矛盾.所以满足条件的直线不存在.

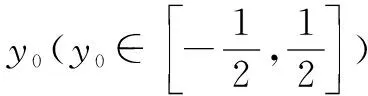
例3 对于函数f(x)(x∈D)，若同时满足以下条件：①f(x)在D上单调递增或单调递减；②存在区间[a,b]⊆D，使f(x)在[a,b]上的值域是[a,b].那么，我们把函数f(x)(x∈D)叫做闭函数.

(1)求闭函数y=-x3符合条件的区间[a,b]；

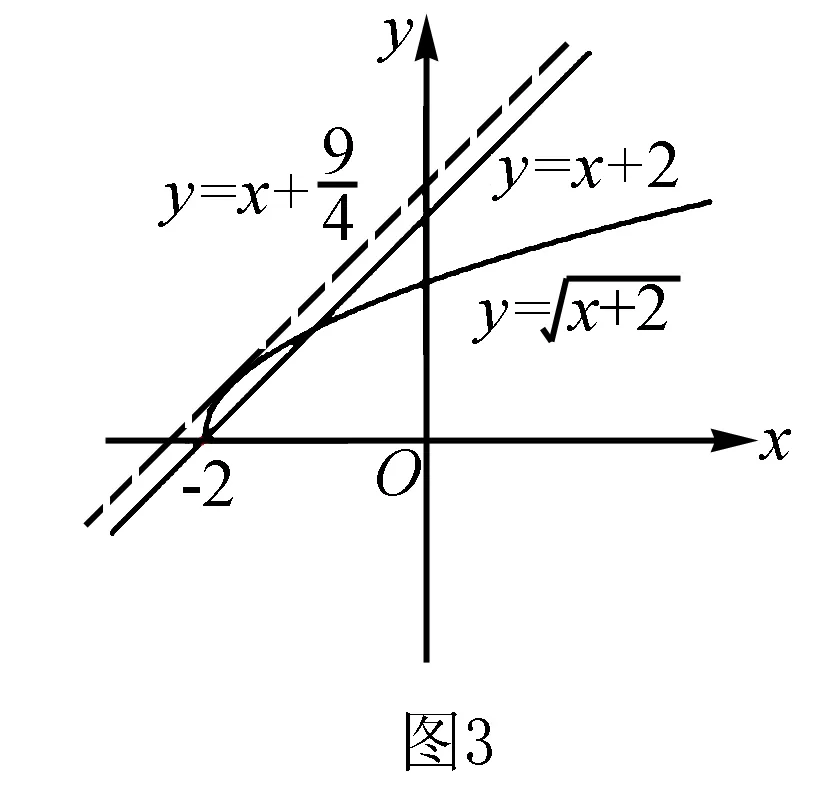
(2)判断函数y=2x-lgx是不是闭函数？若是，说明理由，并找出区间[a,b]；若不是，说明理由；

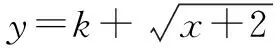
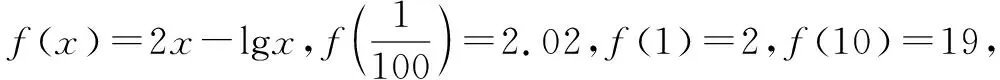
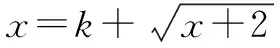
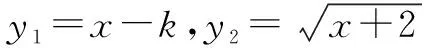
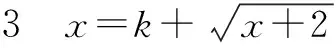
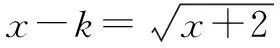
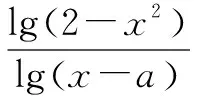
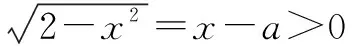
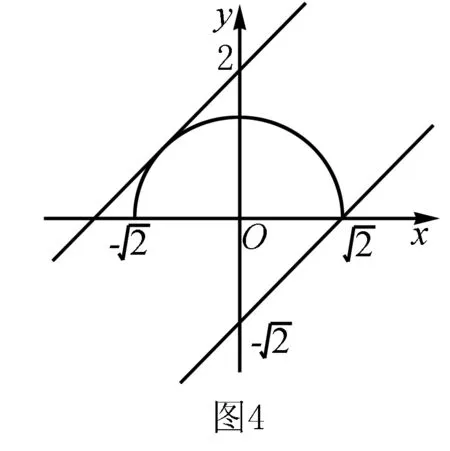
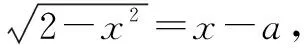
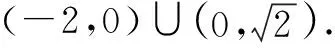
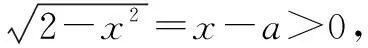
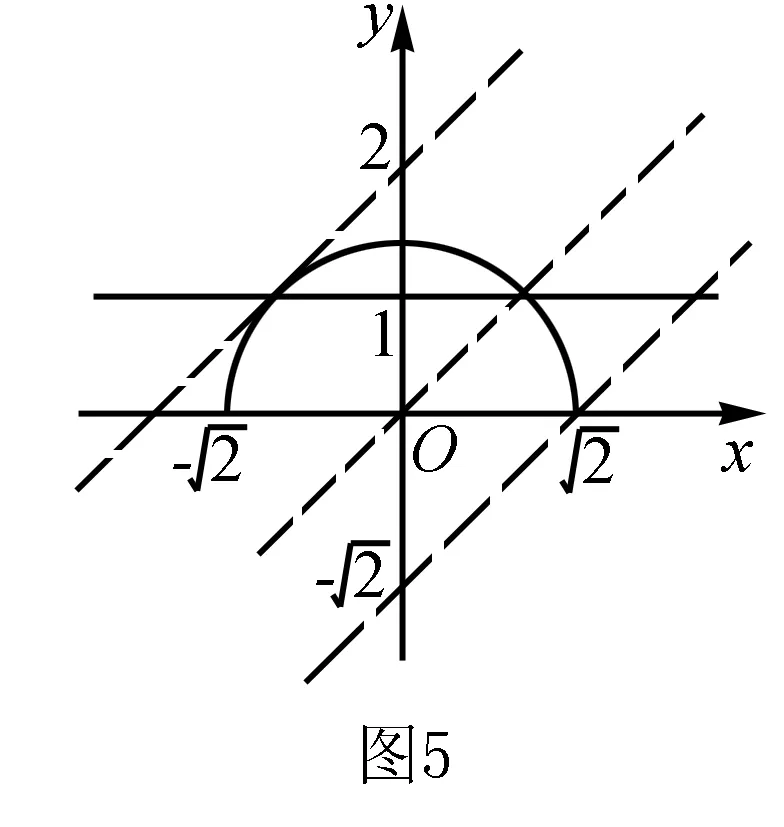
例4 已知动圆过定点P(1,0)，且与定直线L∶x=-1相切，点C在L上.

(1)求动圆圆心的轨迹M的方程；

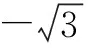
(ⅰ)问：△ABC能否为正三角形？若能，求点C的坐标，若不能，说明理由；

(ⅱ)当△ABC为钝角三角形时，求点C的纵坐标的取值范围.

解(1)由题意，曲线M是以点P为焦点，直线L为准线的抛物线，所以曲线M的方程为y2=4x.

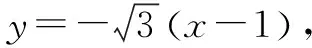
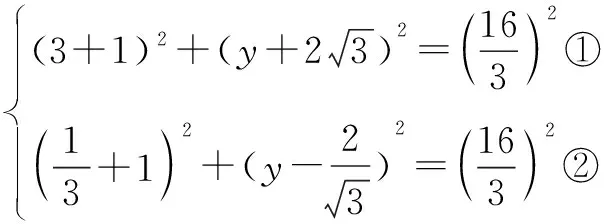
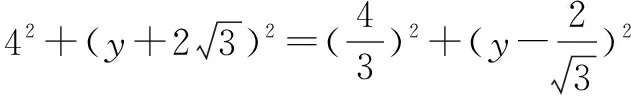
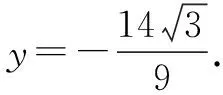
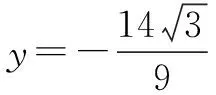
由①②组成的方程组无解，即直线L上不存在点C，使得△ABC为正三角形.

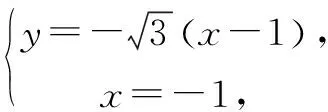
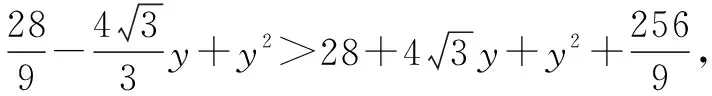
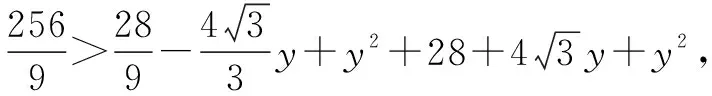
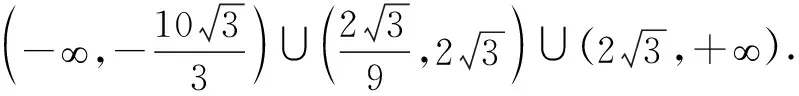
点评在第(2)(ⅰ)小题中，“|BC|=|AB|且|AC|=|AB|”是“△ABC为正三角形”的充要条件，但①-②得到(|BC|=|AC|所满足)的方程③只是结论的必要条件，由等价变形可知①③或②③构成的方程组为结论的充要条件.本题也可根据“△ABC为正三角形”由A,B求出点C的坐标再验证点C的横坐标是否为-1.在第(2)(ⅱ)小题中，首先要确保△ABC的存在性，由于以抛物线的焦点弦为直径的圆与该抛物线的准线相切，故∠ACB不可能为钝角，解答中用余弦定理求解，需要解关于y的一元二次不等式.结合本题中点A,B是固定的，故可先根据CA⊥AB或CB⊥AB利用斜率关系找出临界值，再结合图形求解.