Modified embedded-atom method interatomic potentials for Mg–Al–Ca and Mg–Al–Zn ternary systems

Hyo-Sun Jang,Donghyuk Seol,Byeong-Joo Lee

Department of Materials Science and Engineering,Pohang University of Science and Technology(POSTECH),Pohang 37673,Republic of Korea

Received 9 April 2020;received in revised form 23 August 2020;accepted 6 September 2020

Available online 6 October 2020

Abstract Al,Ca,and Zn are representative commercial alloying elements for Mg alloys.To investigate the effects of these elements on the deformation and recrystallization behaviors of Mg alloys,we develop interatomic potentials for the Al–Ca,Al–Zn,Mg–Al–Ca and Mg–Al–Zn systems based on the second nearest-neighbor modified embedded-atom method formalism.The developed potentials describe structural,elastic,and thermodynamic properties of compounds and solutions of associated alloy systems in reasonable agreement with experimental data and higher-level calculations.The applicability of these potentials to the present investigation is confirmed by calculating the generalized stacking fault energy for various slip systems and the segregation energy on twin boundaries of the Mg–Al–Ca and Mg–Al–Zn alloys,accompanied with the thermal expansion coefficient and crystal structure maintenance of stable compounds in those alloys.

Keywords:2NN MEAM;Interatomic potential;Mg–Al–Ca;Mg–Al–Zn;Atomistic simulation.

1.Introduction

With density of 1.74g/cm3near room temperature(RT),magnesium(Mg)is the lightest structural metal.This light metal has been emerging as a next generation material in the transportation industry[1,2].Despite the emergence,the industrial utilization of Mg has been limited because of its poor formability at RT[2].The poor formability is known to originate from the strong basal texture of pure Mg[3].Because the texture is evolved during deformation and recrystallization processes,to improve the formability,various elements have been alloyed with Mg to modify the deformation and recrystallization behaviors[4–7].

The typical alloying elements that compose the representative commercial Mg alloys AZ31 and ZX31 are aluminum(Al),calcium(Ca),and zinc(Zn).Extensive efforts have been devoted to clarify the effects of these elements on the deformation and recrystallization behaviors of these alloys[4,7–13].As a result,the alloying effects on the slip,twinning,and grain boundary(GB)segregation,which are closely related to the deformation and recrystallization behaviors[14,15],were partially revealed.The addition of a small amount of Al has been reported to activate the non-basal slip[10],but retard the nucleation and growth of the tension twin[11];the addition of Ca activates the compression twin[12],and the addition of Zn activates the non-basal slip[13]and the tension twin[4].The GB segregation occurs in all binary Mg alloys containing Al,Ca,and Zn[7–9].Despite the aforementioned efforts,the above information is insufficient to understand the slip,twinning,and recrystallization behaviors varying with composition in the Mg–Al–Ca[16,17],Mg–Al–Zn[18,19],and Mg–Zn–Ca[4–6,20]alloys.For this reason,further studies should be carried out to clarify the effect of the multicomponent Mg alloys.To study the effect,it is necessary to observe the interaction between different elements during the deformation and recrystallization processes.Such observation requires a tool that can analyze samples with complex and less symmetric structures such as the non-basal slip,twin,and GB.This analysis can be effectively performed through a large-scale atomistic simulation that can analyze atomic behavior of up to millions of atoms,compared to experiments and first-principles calculations.

The large-scale atomistic simulation requires(semi-)empirical interatomic potentials that can describe associated alloy systems.Previous studies have developed the interatomic potentials for multicomponent Mg alloys containing Al,Ca,and Zn:Mg–Al–Ca[21],Mg–Al–Zn[22],and Mg–Zn–Ca[23].The Mg–Zn–Ca potential has been reported to well reproduce the generalized stacking fault energy(GSFE)and the segregation energy on GB of the Mg–Zn–Ca alloys[23].The GSFE and segregation energy are related to the deformation[24]and recrystallization[15]behaviors,respectively.This potential thus can be utilized to study the effect of alloying elements on the deformation and recrystallization behavior.However,even with the previous efforts,the Mg–Al–Ca and Mg–Al–Zn potentials should be developed further.This is because the Mg–Al–Ca potential was developed for investigating metallic glasses[21],not crystalline structures.The Mg–Al–Zn potential was developed[22]to study the dilute Mg solid solution.However,this potential also has room for further improvement,e.g.the binding energy of Al and Zn in a Mg-rich hcp solid solution matrix and the GSFE on slip planes.For a more comprehensive and detailed study on the deformation and recrystallization behaviors of the Mg–Al–Ca and Mg–Al–Zn alloys,it is necessary to re-develop the interatomic potentials for the Mg–Al–Ca and Mg–Al–Zn systems.

A multicomponent interatomic potential is developed based on the interatomic potentials of constituent lower-order alloy systems.This means that developing the Mg–Al–Ca and Mg–Al–Zn ternary potentials requires the Mg,Al,Ca,and Zn unary and the Mg–Al,Mg–Ca,Mg–Zn,Al–Ca,and Al–Zn binary potentials.Our group has developed the Mg[25],Al[26],Ca[27],and Zn[28]unary and the Mg–Al[25],Mg–Ca[27],and Mg–Zn[28]binary potentials,which can reliably reproduce the structural,elastic,and thermodynamic properties of relevant alloy systems,based on the second nearest-neighbor modified embedded-atom method(2NN MEAM[29–31])formalism.The developed Mg unary and binary potentials successfully reproduce the GSFE on the basal and non-basal slip planes[23,27,28,32],as well as the GB energy of pure Mg[33]and the GB segregation in Mg–Zn alloys[33].In addition,the Mg unary potential is reported to adequately reproduce the core structures of〈c+a〉edge and screw dislocations[32].Because of the reliable reproducibility,we used those 2NN MEAM potentials to develop the Mg–Al–Ca and Mg–Al–Zn potentials.The resultant Mg–Al–Ca and Mg–Al–Zn potentials can also be easily extended to various commercial multicomponent Mg alloy systems,combined with the previously developed Mg-X(X=Li[34],Nd[35],Pb[35],Sn[27],and Y[27])and Mg–Zn–Ca[23]potentials.The development of the Mg–Al–Ca and Mg–Al–Zn ternary potentials requires the Al–Ca and Al–Zn binary potentials.However,the Al–Ca potential applicable to crystalline structures has not been developed yet.For the Al–Zn system,there was an MEAM potential applicable to the Mg solid solutions[22],but we could not use this potential in the present work because the description for pure Zn in this potential[22]was different from ours[28],which was also used for the Mg–Zn[28]and the Mg–Zn–Ca[23]systems.

In this study,we developed the 2NN MEAM potentials for the Al–Ca and Al–Zn binary and the Mg–Al–Ca and Mg–Al–Zn ternary systems to study the deformation and recrystallization behaviors of the Mg–Al–Ca and Mg–Al–Zn alloys.This article reports the brief formalism,procedure for the potential parameter determination and the validity of the developed potentials.The validity is examined by comparing the calculated fundamental material properties using the developed potentials with data from the literature.

2.Formalism and determination of interatomic potential parameters

Since a full description on the 2NN MEAM formalism has been published in the literature[29,36],we briefly introduced the concept of the formalism and many-body screening.The total energy of a system in the MEAM is approximated as

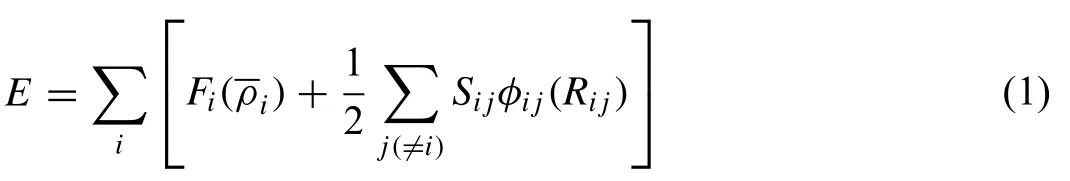
where Fiis the embedding function,is the background electron density at site i.Sijandφij(Rij)are the screening factor and the pair interaction between atoms i and j separated by a distance Rij,respectively.For general calculations of energy,the functional forms for the two terms on the right hand side of Eq.(1),Fiandφij,should be given.The background electron density at a site is computed considering directionality in bonding.A specific form is given to the embedding function Fi,but not to the pair interactionφij.Instead a reference structure where individual atoms are on the exact lattice points is defined and the total energy per atom of the reference structure is estimated from the zero-temperature universal equation of state of Rose et al.[37].Then,the value of the pair interaction is evaluated from the known values of the total energy per atom and the embedding energy,as a function of nearestneighbor distance.

In the original MEAM[38],only first nearest-neighbor interactions are considered.The neglect of the second nearestneighbor and more distant nearest-neighbor interactions is made effective by the use of a strong many-body screening function[39].The consideration of the second nearestneighbor interactions in the 2NN MEAM[26,29,36,40]is affected by adjusting the screening parameters so that the many-body screening becomes less severe.In more detail,the many-body screening function between atoms i and j,Sij,is defined as the product of the screening factors,Sikj,due to all other neighbor atoms k:

Sikjis computed using a simple geometric construction.Imagine an ellipse on an x,y plane,passing through atoms,i,k and j with the x-axis of the ellipse determined by atoms i and j.The equation of the ellipse is given by,

For each k atom,the value of parameter C can be computed from relative distances among the three atoms,i,j and k,as follows:

where Xik=(Rik/Rij)2and Xkj=(Rkj/Rij)2.The screening factor,Sikjis defined as a function of C as follows:

where Cminand Cmaxare the limiting values of C determining the extent of screening and the smooth cutoff function is

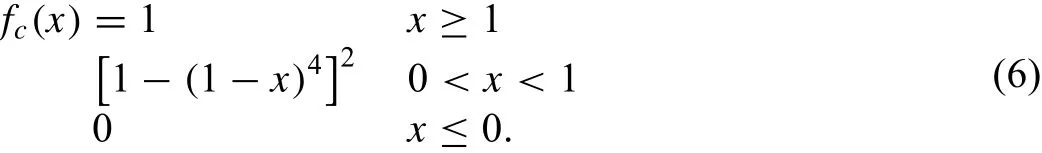
The basic idea for the screening is as follows:First define two limiting values,Cmaxand Cmin(Cmax>Cmin).Then,if the atom k is outside of the ellipse defined by Cmax,it is thought that the atom k does not have any effect on the interaction between atoms i and j.If the atom k is inside of the ellipse defined by Cminit is thought that the atom k completely screens the i-j interaction,and between Cmaxand Cminthe screening changes gradually.In the numerical procedure of simulation the electron density and pair potential are multiplied by the screening function Sij,as is done in Eq.(1).Therefore,Sij=1 and Sij=0 mean that the interaction between atoms i and j is unscreened and completely screened,respectively.In addition to the many-body screening function,a radial cutoff function which is given by fc[(rc-r)/Δr]where rcis the cutoff distance andΔr(0.1 °A)is the cutoff region,is also applied to the atomic electron density and pair potential[39].The radial cutoff distance is chosen so that it does not have any effect on the calculation results due to the many-body screening.This is only for the computational convenience,that is,to save the computation time.Detailed explanation for the formalism is provided in Appendix A.

Using this formalism,we developed of interatomic potential of the Al–Ca and Al–Zn binary and the Mg–Al–Ca and Mg–Al–Zn ternary systems by determining their potential parameters.The development of the binary potentials is conducted first,followed by the development of the ternary potentials.The unary and binary potential parameters utilized in the present development are listed in Table 1 and Table 2.

2.1.Development of the Al–Ca and Al–Zn binary potentials

The 2NN MEAM potential for a binary system comprises thirteen model parameters along with twenty-eight model parameters for the two sub-unary systems.The binary model parameters consist of cohesive energy(Ec),equilibrium nearestneighbor distance(re),bulk modulus(B),a parameter related to the pressure derivative of bulk modulus(d),the ratio between atomic electron density scaling factors(ρ0),and eight many-body screening parameters(four Cminand four Cmax).

The Ec,re,B,and d parameters are used to describe the universal equation of state of a given reference structure,so they can be determined directly from material properties of the reference structure if the structure exists in a phase diagram.The Al–Ca binary phase diagram contains monoclinic Al4Ca,triclinic Al2Ca,D13Al14Ca13,and C15 Al3Ca8intermetallic compounds[41].However,the crystal structures of these compounds are too complicated to serve as the reference structure.This is because the(2NN)MEAM potential formalism can use only a few,simple crystal structures in which all of the second nearest neighboring atoms are composed of the same element,as the reference structure.Thus,a hypothetical B1 AlCa compound was chosen as the reference structure of the Al–Ca potential,considering that both Al and Ca have fcc structures at RT.The Al–Zn binary phase diagram does not contain any stable intermetallic compounds[42],but we could obtain material properties for a hypothetical L12Al3Zn compound from a first-principles calculation[43].Hence,the L12Al3Zn compound was chosen as the reference structure of the Al–Zn potential.

Since the chosen reference structures of the two systems were all hypothetical compounds,the Ec,re,and B parameters were optimized to reproduce the thermodynamic,structural,and elastic properties of stable phases in the relevant binary systems.The B parameter of the Al–Zn system could not be optimized as that of the Al–Ca system due to the lack of information on the elastic properties of stable phases.Instead,we could obtain the information on bulk modulus of a hypothetical L12Al3Zn compound from a first-principles calculation[43],and could assign a value to the B parameter using this information.The Cminand Cmaxparameter values of the Al–Ca and Al–Zn systems were fixed to fit the fundamental material properties of their relevant systems.The Cmin(Al–Ca–Al)and Cmin(Ca–Al–Ca)parameter values were fixed to fit the enthalpy of formation of stable compounds and to maintain the structural stability of the stable compounds.The Cmax(Al–Ca–Al)parameter value was fixed to make the enthalpy of formation of hypothetical L10compound less stable.The Cmin(Al–Al–Ca),Cmax(Al–Al–Ca)and Cmax(Al–Ca–Ca)parameter values were fixed to maintain the structural stability of the stable D13Al4Ca compound.The Cmin(Al–Zn–Al),Cmin(Al–Al–Zn),Cmin(Al–Zn–Zn),Cmax(Al–Zn–Al),Cmax(Al–Al–Zn),and Cmax(Al–Zn–Zn)parameter values were fixed to fit the enthalpy of mixing of fcc solid and liquid solutions.The other parameter values were set from each assumption presented in Table 3.Among the four stable compounds in the Al–Ca system,the monoclinic Al14Ca13and triclinic Al3Ca8compounds,whose crystal structures were too complex to be described by the 2NN MEAM formalism,were excluded from the parameterization procedure.For both systems,the d parameters were given the average value of the pure constituent elements.Theρ0Al:ρ0Caandρ0Al:ρ0Znra-tios were also given default assumed values.The determined potential parameter sets of the Al–Ca and Al–Zn binary systems are listed in Table 3.

Table 12NN MEAM potential parameter sets for pure Mg[25],Al[26],Ca[27],and Zn[28].The units of the cohesive energy Ec,equilibrium nearest-neighbor distance re,and bulk modulus B are eV,°A,and 1012 dyne/cm2,respectively.The reference structures are hcp for Mg and Zn,and fcc for Al and Ca.

Table 22NN MEAM potential parameter sets for the Mg-Al[25],Mg-Ca[27],and Mg-Zn[28]binary systems.The units of the cohesive energy Ec,equilibrium nearest-neighbor distance re,and bulk modulus B are eV,°A,and 1012 dyne/cm2,respectively.

Table 32NN MEAM potential parameter sets for the Al-X(X=Ca or Zn)systems.The units of the cohesive energy Ec,equilibrium nearest-neighbor distance re,and bulk modulus B are eV,°A,and 1012 dyne/cm2,respectively.

2.2.Development of the Mg–Al–Ca and Mg–Al–Zn ternary potentials

Similar to binary potentials,the 2NN MEAM potential for a ternary system comprises sub-unary and sub-binary potential parameters as well as three Cmin(i-k-j)and three Cmax(i-k-j)ternary parameters,which represent the degree of screening by an atom of a third element(k)to the interaction between two neighboring atoms(i and j)of different elements.If the two elements(j and k)are relatively similar to each other compared to one element(i),then we can assume that the degree of screening by an i atom to the interaction between j and k atoms[Cminand Cmax(j-i-k)]is an average between the degree of screening by the i atom to the j-j[Cminand Cmax(j-i-j)]and k-k[Cminand Cmax(k-i-k)]interactions.In a similar way,the degree of screening by a j(or k)atom to the interaction between i and k(or j)atoms[Cminand Cmax(i-j-k)or Cminand Cmax(i-k-j)]is an average between those to the i-j[Cminand Cmax(i-j-j)]and i-k[Cminand Cmax(i-k-k)]interactions.This assumption has already been applied to develop the 2NN MEAM potential for the Mg–Zn–Ca system[23].As mentioned before,the developed Mg–Zn–Ca potential reason-ably reproduced the fundamental material properties,GSFE,segregation energy,and volumetric misfit strain of the Mg–Zn–Ca alloys.In addition,using this assumption,other 2NN MEAM potentials have been developed for ternary systems containing both interstitial(Fe–Ti–C,Fe–Ti–N[31],Fe–Nb–C,and Fe–Nb–N[44])and substitutional solute atoms(V–Pd–Y[45]and Fe–Cr–Ni[46]).These potentials have been evaluated to reproduce their relevant alloy properties correctly.

Table 42NN MEAM potential parameter sets for the Mg–Al–X(X=Ca or Zn)ternary systems.

Due to the good applicability,this assumption was applied to develop the Mg–Al–Ca and Mg–Al–Zn potentials,assuming that Al and Ca with an fcc structure are relatively similar to each other compared to Mg with an hcp structure,and that Mg and Zn with an hcp structure are relatively similar to each other compared to Al with an fcc structure,respectively.Based on this assumption,the ternary Cminand Cmaxparameters for the Mg–Al–Ca and Mg–Al–Zn systems were determined automatically from the corresponding parameters for the sub-binary systems,as listed in Table 4.

3.Calculation of fundamental material properties

In this section,fundamental material properties of the Al–Ca and Al–Zn binary and Mg–Al–Ca and Mg–Al–Zn ternary systems are calculated and compared with data from the literature,in order to examine the reliability and transferability of the presently developed potentials.The examined properties are classified into properties to confirm the fitting quality and the transferability.For the Al–Ca system whose phase diagram contains stable intermetallic compounds[41],the properties of the stable compounds are utilized to examine its fitting quality,and its transferability is examined through the properties of solutions.The fitting quality of the Al–Zn system which does not contain any stable compounds on the phase diagram[42]was examined by calculating the properties of solutions and hypothetical compounds.All properties examined for ternary systems are those to confirm the transferability,because the ternary properties were not used for parameter fitting.The material properties were calculated at 0K except for the enthalpy of mixing of liquid solutions and the structural stability of compounds at finite temperatures.The calculations were carried out using an in-house molecular dynamics(MD)and statics code,KISSMD[47],and the large-scale atomic/molecular massively parallel simulator(LAMMPS)package[48].A periodic boundary condition was set in all directions except the GSFE calculation.In all calculations,the radial cutoff distance was 6.0 °A that is larger than the second nearest-neighbor distances of Mg,Al,Ca,and Zn.

3.1.Calculated material properties of the Al–Ca binary system

We first examined the structural,elastic,and thermodynamic properties of stable compounds of the Al–Ca binary system.The calculated lattice parameters and elastic moduli for the stable compounds are listed in Table 5 along with data in the literature.The calculated lattice parameters of the D13Al4Ca compound are in reasonable agreement with experimental data[49]and a first-principles calculation[50].Those of the C15 Al2Ca compound are slightly larger than experimental data[51–53]and first-principles calculations[50,53–55].A great amount of effort had been made during the parameterization to reproduce the lattice parameter of the C15 Al2Ca compound closer to the literature values.However,the reproducibility of the lattice parameter could not be improved without losing structural stability of the stable D13Al4Ca and C15 Al2Ca compounds.For this reason,we optimized the potential parameters to satisfy both properties simultaneously,and the lattice parameter listed in Table 5 is the calculation result based on the final optimized parameter set.The calculated elastic moduli of the C15 Al2Ca compound are consistent with experimental data[52,56]and first-principles calculations[54,55,57,58].The enthalpy of formation of the stable compounds as well as various hypothetical compounds were calculated to confirm whether the stable compounds are predicted as the most stable phases.The calculated enthalpy of formation is presented in Fig.1 and Table 6 in comparison with literature data.The enthalpy of formation of the D13Al4Ca compound is more negative than the literature data[41,50,59–64]while that of the C15 Al2Ca compound is in good agreement with the literature data[41,50,64,53,57–63].A lot of effort had been made during the parameterization to reproduce the enthalpy of formation of the D13Al4Ca compound closer to the literature values.However,similar to the lattice parameter,the reproducibility could not be improved without losing structural stability of the stable D13Al4Ca compound.For this reason,we optimized the potential parameters to satisfy both properties simultaneously,and the enthalpy of formation presented in Fig.1 and Table 6 is the calculation result based on the final optimized parameter set.Both stable compounds are calculated to be the most stable phases at corresponding compositions in the Al–Ca systems.As stated in Section 2.2,there are two more stablecompounds in the Al–Ca system:monoclinic Al14Ca13and triclinic Al3Ca8,but we could not calculate their properties.This is because their crystal structures were too complex to be described by the 2NN MEAM formalism,so they were not(meta)stable according to the present potential.

Table 5Calculated lattice parameters(°A)and elastic moduli(GPa)of AlxCay intermetallic compounds using the present 2NN MEAM potential,in comparison with experimental data(Exp.)and first-principles calculations(F.P.calc.).

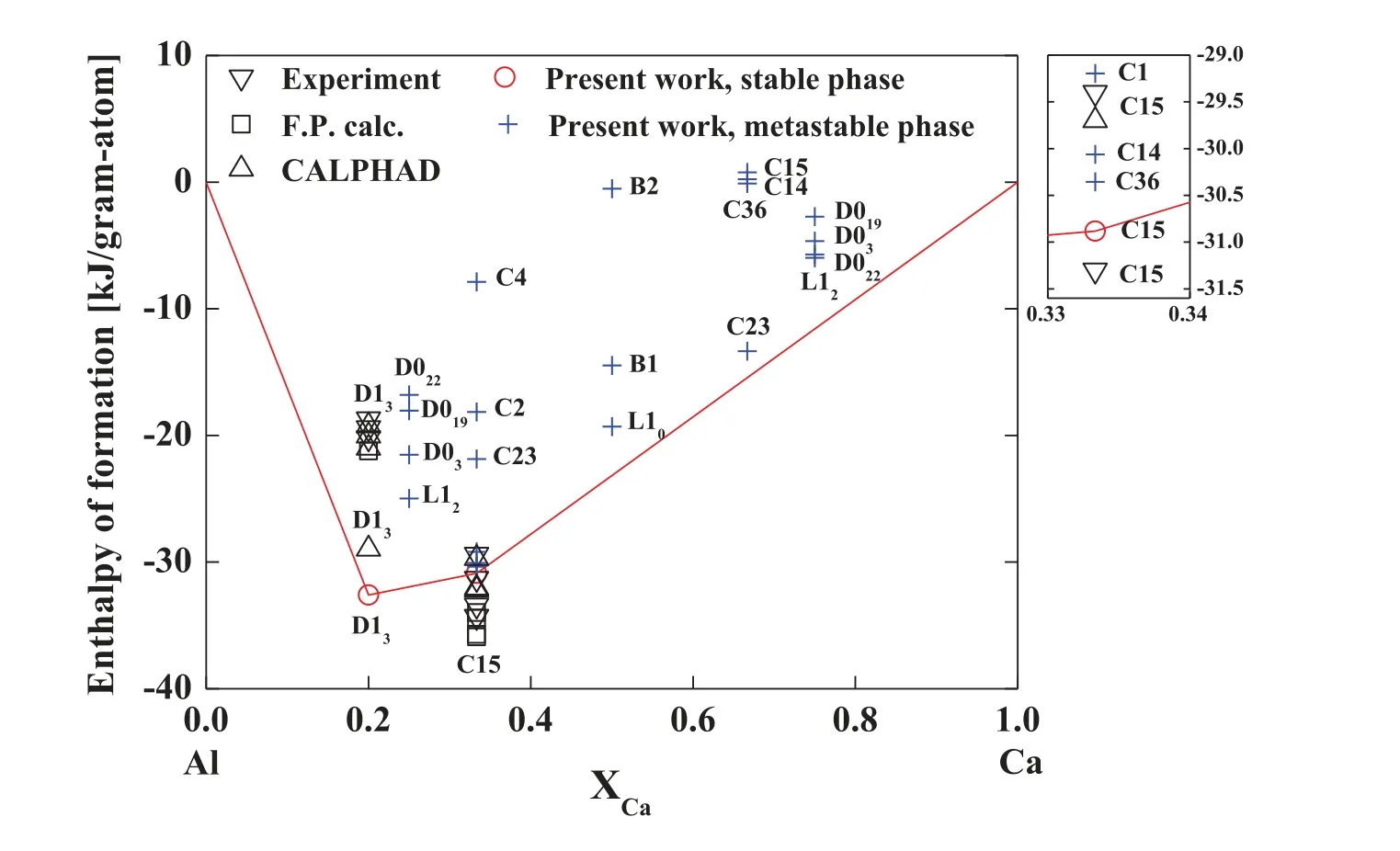
Fig.1.Enthalpy of formation of stable and hypothetical compounds of the Al–Ca binary system at 0K according to the present 2NN MEAM potential,in comparison with experimental data[59–61,63],first-principles calculations[43,50,53,57,58,81],and CALPHAD calculations[41,62–64].

Next,the thermodynamic property of solutions of the Al–Ca binary system was examined through the calculation of enthalpy of mixing of liquid solutions.The calculation was performed through an MD simulation based on the velocity Verlet algorithm and the Parrinello/Rahman NPT ensemble at finite temperatures.To create a liquid sample,we raised the temperature of an fcc sample to 1800K.The liquid sample was cooled to 1400K,which was similar to the temperature used in a recently published CALPHAD calculation[64].The calculated enthalpy of mixing is presented in Fig.2 along with data from the literature.The calculated enthalpy of mixing of the Al–Ca liquid solutions is more negative than experimental data[65–67]and the CALPHAD calculation[64].The minimum point in the calculated enthalpy of mixing seems to be rather too close to the Al-rich side when compared to literature data[64–67].This is in line with that the calculated enthalpy of formation of Al4Ca compound is more negative than that of Al2Ca compound contrary to literature information as shown in Fig.1 and Table 6.If the description for the solid compounds is improved in any future redevelopment work of the Al–Ca interatomic potential,the description for the liquid enthalpy of mixing would also be improved.

Fig.2.Enthalpy of mixing of liquid solutions of the Al–Ca binary system according to the present 2NN MEAM potential,in comparison with experimental data[65–67]and a CALPHAD calculation[64].The error bars inside the red squares denote the standard deviation.

Table 6Calculated enthalpy of formationΔHf(kJ/gram-atom)of AlxCay intermetallic compounds using the present 2NN MEAM potential,in comparison with experimental data,and first-principles and CALPHAD calculations.

3.2.Calculated material properties of the Al–Zn binary system

As mentioned above,the Al–Zn phase diagram does not contain any stable compound but contains a wide range of Al-rich fcc solid solution[42]whose structural[68–73]and thermodynamic[74–79]properties have been reported well.There is also available information for the thermodynamic property of Al–Zn liquid solutions[78–80]and the structural,elastic,and thermodynamic properties of a hypothetical L12Al3Zn compound[43].For these reasons,the reliability of the Al–Zn system was examined through the structural property of the solid solution and the hypothetical compound,the elastic property of the hypothetical compound,and the thermodynamic property of the solid and liquid solutions and the hypothetical compound.

The structural and elastic properties were examined through the calculation of lattice parameters of the solid solution and lattice parameters and elastic moduli of the hypothetical compound.The lattice parameters of the solid solution were calculated for eight samples(4000 atoms)of random,disordered fcc solid solutions containing 0 to 30 at% Zn.The same calculations were carried out independently using three different samples for each composition to avoid the statistical error originated from the distribution of Zn atoms in samples.The average values of the calculated lattice parameters of the solid solutions at 0K are presented in Fig.3,in comparison with experimental data at 298K[68–73]and the other MEAM calculation at 0K[22].The standard deviation values of the present calculation are listed in Table S1.The calculated lattice parameter decreases with the Zn content,and its composition dependence is consistent with experimental data.This consistency is higher than that between the experimental data and the other MEAM calculation.The calculated lattice parameter and elastic moduli of the hypothetical L12Al3Zn compound are listed in Table 7 along with literature data.The present calculations for the lattice parameter and elastic moduli of the L12Al3Zn compound are consistent with a first-principles calculation[43].

Fig.3.Lattice parameter of Al-rich fcc Al–Zn solid solutions at 0K according to the present 2NN MEAM potential,in comparison with experimental data[68–73]and the other MEAM calculation[22].

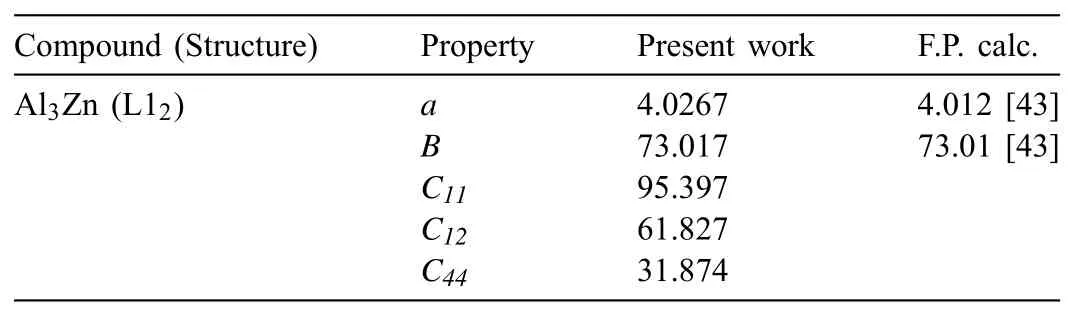
Table 7Calculated lattice parameter(°A)and elastic moduli(GPa)of a hypothetical L12 Al3Zn intermetallic compound using the present 2NN MEAM potential,in comparison with a first-principles calculation.

The thermodynamic property was examined through the calculation of enthalpy of mixing of the solid and liquid solutions,and enthalpy of formation of solid solutions and hypothetical compounds.The enthalpy of mixing was calculated for random,disordered fcc solid solutions containing 0 to 100 at% Zn.Each sample consisted of 1000 atoms.The MD simulation for the fcc solid solutions was performed at 650K,which was similar to the temperature used in the literature[74–79].To conduct the simulation for the liquid solutions,we created liquid samples by raising the temperature of fcc samples to 1500K.The liquid samples were cooled to 950K,which was similar to the temperature used in the literature[78–80].The enthalpy of formation was also calculated for Al–Zn hcp solid solutions(the Al–Zn phase diagram also contains a narrow range of Zn-rich hcp solid solution[42])and other hypothetical compounds.The calculated enthalpy of mixing and enthalpy of formation are presented in Fig.4 in comparison with data from the literature.The calculated enthalpy of mixing of the Al–Zn fcc solid solution in Fig.4a is consistent with two experimental data sets[74,75]out of four considered[74–77]and a recently published CALPHAD calculation[79].The calculated enthalpy of mixing of the Al–Zn liquid solution is also comparable with experimental data[80]and CALPHAD calculations[78,79](Fig.4b).In Fig.4c,the enthalpy of formation of the Al–Zn fcc and hcp solid solutions and of the hypothetical AlxZnycompounds are all positive.The positive enthalpy of formation of the hypothetical compounds is also reported in first-principles calculations[43,81].This agrees well with the finding that no compound should be stable and the most stable phase structure at low temperatures on the Al–Zn phase diagram is a mixture of Al-rich fcc and Zn-rich hcp solid solutions[42].It should be mentioned here that it was possible to modify the parameters to make those enthalpy of mixing properties closer to the CALPHAD calculation reported by Wasiur-Rahman et al.[79].However,this modification increased the deviation of the present enthalpy of formation of the hypothetical L10,D022,and L12compounds from the first-principles calculations.Since the present reproducibility is also sufficient,the present potential parameters were finally selected.

3.3.Calculated material properties of the Mg–Al–Ca and Mg–Al–Zn ternary systems

The Mg–Al–Ca ternary phase diagram contains two ternary intermetallic compounds,C36(Mg,Al)2Ca[82]and Pbcm MgAl3Ca4[83],as well as MgxAly,MgxCay,and AlxCaybinary intermetallic compounds and Mg-rich hcp,Al-rich fcc,and Ca-rich fcc solid solutions[84].The Mg–Al–Zn ternary phase diagram also contains two ternary intermetallic compounds,Im¯3 Mg32(Al,Zn)49[85]and Pbcm Mg24(Al,Zn)17[86],in addition to MgxAlyand MgxZnybinary intermetallic compounds and Mg-rich hcp,Al-rich fcc,and Zn-rich hcp solid solutions[87].Among the ternary compounds,MgAl3Ca4was mechanically unstable according to the present potential,and therefore only 0K material properties were examined.

We first calculated the structural and thermodynamic properties of the ternary compounds in each ternary system to examine the transferability of the ternary potentials.Table 8 lists the calculated lattice parameters and enthalpy of formation of the ternary compounds along with literature data.The calculated lattice parameters of(Mg,Al)2Ca,Mg32(Al,Zn)49,and Mg24(Al,Zn)17compounds are in reasonable agreement with experimental data[82,85,88–90]while the agreement for those of MgAl3Ca4is worse.The calculated enthalpy of formation of(Mg,Al)2Ca is more negative than the CALPHAD calculation[91],and those of MgAl3Ca4,Mg32(Al,Zn)49,and Mg24(Al,Zn)17compounds are less negative than firstprinciples calculations[92,93].Despite this discrepancy,the present enthalpy of formation values have the same negative sign as the literature data[91–93],and are closer to the literature data[91,93]than the other MEAM calculation[22].Also,the calculated enthalpy of formation of the MgxAlyZnzternary compounds shows the same trend as the first-principles calculation[93]in that Mg32(Al,Zn)49is more stable than Mg24(Al,Zn)17.Unlike binary properties,ternary properties are difficult to improve by adjusting the potential parameters.Thus,the ternary properties were used to confirm not the fitting quality,but the transferability of the developed potential.We also calculated the binding energy of Al–Ca and Al–Zn solute pairs in the Mg matrix to further evaluate the transferability of the developed ternary potentials.As shown in Table 9,the developed Mg–Al–Ca and Mg–Al–Zn potentials reasonably reproduce the binding energy,which demonstrates that these potentials can be utilized to study the deformation and recrystallization behaviors in Mg solid solutions.

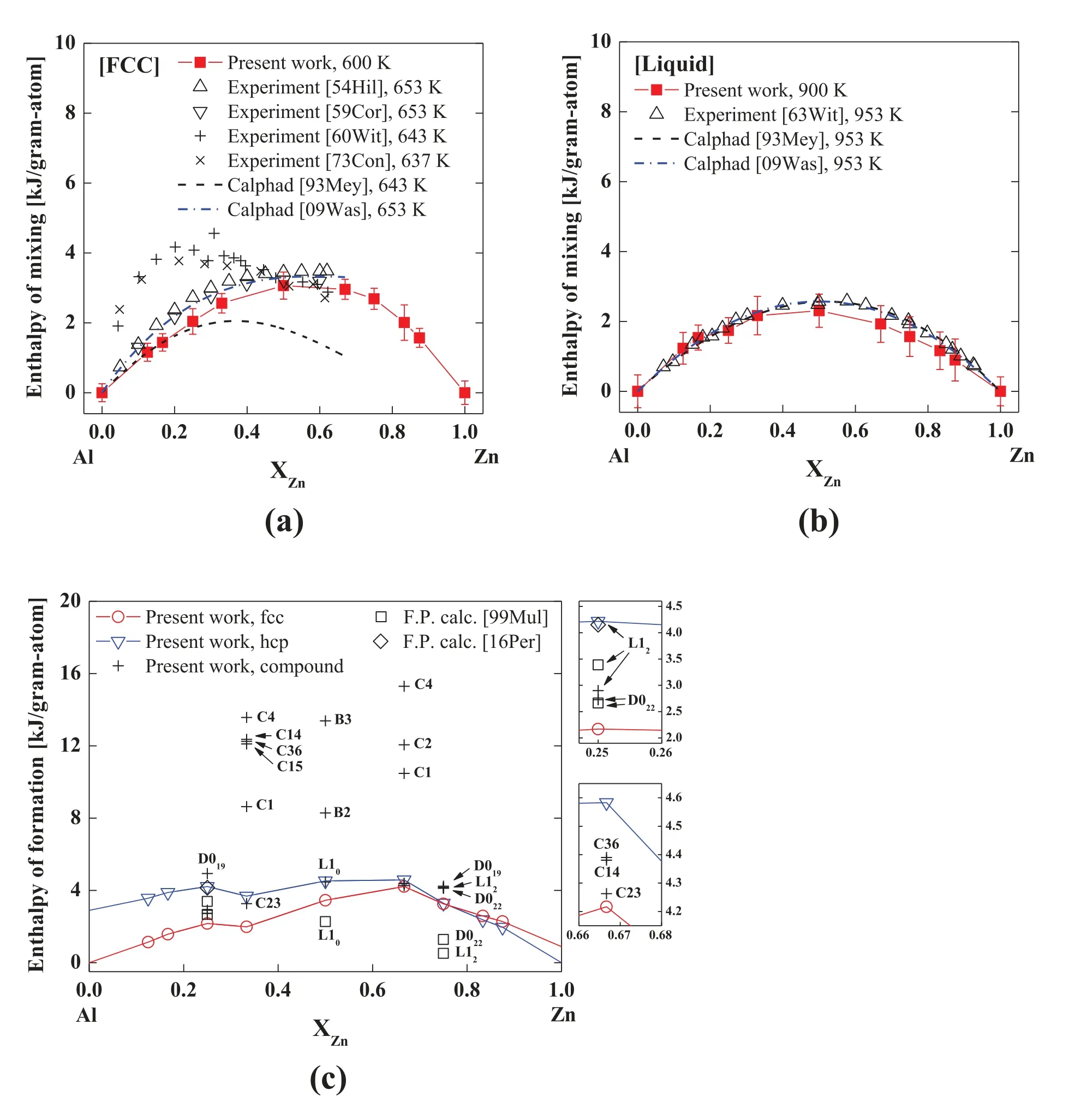
Fig.4.Enthalpy of mixing of(a)fcc solid and(b)liquid solutions at finite temperatures and(c)enthalpy of formation of metastable fcc and hcp solid solutions and hypothetical compounds at 0K of the Al–Zn binary system according to the present 2NN MEAM potential,in comparison with experimental data[74–77,80],first-principles calculations[43,81],and CALPHAD calculations[78,79].The error bars denote the standard deviation.

In addition to the ternary compound properties,we examined the transferability of the developed potentials in the solid solutions.Among the solid solutions,the Mg-rich hcp solid solution is the most important when considering the purpose of the present work.Thus,the transferability of the developed potentials was examined in the Mg-rich solid solution by calculating the binding energy of Al–Ca and Al–Zn solute pairs in the Mg matrix and comparing the results with firstprinciples calculations.The calculation was performed for an hcp sample(6nm×3nm×5nm)consisting of 4000 atoms:one Al atom,one Ca(or Zn)atom,and 3998 Mg atoms.The binding energy was obtained by subtracting the total energy of the sample when the two solute atoms are distant from the total energy when these atoms are neighboring.A negative binding energy indicates favorable binding.The neighboring solute pairs could be located in the same or different basal planes.We denoted these locations as“in”and“out”,respectively,and calculated the binding energy for both locations.For comparison,the same binding energy was obtained in the present work from a first-principles calculation using an hcp sample(1.3nm×1.0nm×1.7nm)consisting of 96 atoms.The first-principles calculation used a 4×6×3 Monkhorst–Pack k-point mesh and considered an energy–volume equation of state(EOS)to obtain the equilibrium energy value.The binding energy values calculated using the present interatomic potentials are listed in Table 9,and are compared with the first-principles calculations performed in the present study and from the literature[94].The binding energy of the Al–Ca solute pair for the“in”model according to the potential-based calculation is more negative than that obtained in the firstprinciples calculations,while the energy for the“out”model is similar in both calculations.The binding energy of the Al–Zn solute pair of both models according to the potential-based calculation is more positive than the first-principles calculations.However,the discrepancy is smaller than the difference between the first-principles calculation and the other MEAM calculation[22],specifically for the“out”model.

Table 8Calculated lattice parameters(°A)and enthalpy of formationΔHf(kJ/gram-atom)of MgxAlyCaz and MgxAlyZnz intermetallic compounds using the present 2NN MEAM potentials,in comparison with literature data.

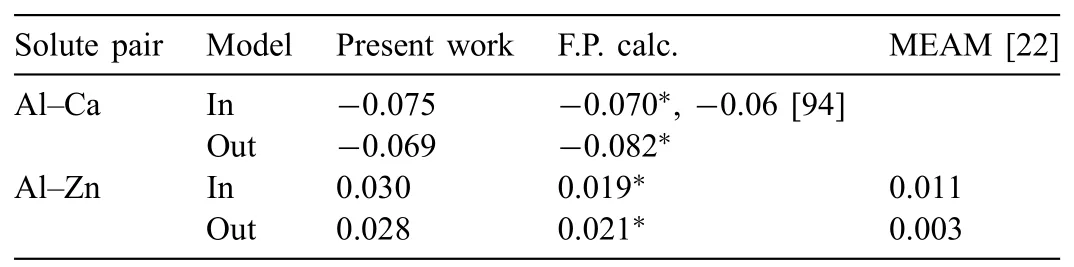
Table 9Calculated binding energy(eV)for the 1NN solute pairs of Al–Ca and Al–Zn in Mg-rich hcp solid solution matrix using the present 2NN MEAM potentials,in comparison with first-principles and the other MEAM calculations.The“in”and“out”models indicate that the solute pair is located in the same and different basal plane,respectively.Note that negative energy indicates energetically favorable binding.

The ternary potentials were developed to study the deformation and recrystallization behaviors of the Mg–Al–Ca and Mg–Al–Zn alloys.Thus,in addition to the above-mentioned fundamental material properties,the potentials should be confirmed for their transferability for the deformation and recrystallization behaviors.The representative property related to the deformation behavior is the GSFE[24],and thus the GSFE of the Mg–Al–Ca and Mg–Al–Zn alloys was calculated along with that of the Mg–Al,Mg–Ca,and Mg–Zn binary alloys and pure Mg.The calculation was conducted for samples with an I2-type stacking fault(SF)on basal{0001}<10¯10>,basal{0001}<1¯210>,prismatic{10¯10}<1¯210>,pyramidal I{10¯11}<1¯210>,and pyramidal II{11¯22}<11¯23>slip systems;each sample had 48,40,36,and 40 stacking layers on its slip plane,respectively.The samples for the alloy systems were created by converting several Mg atoms on the stacking fault(SF)plane into solute atoms.To compare the present calculation to first-principles calculations more precisely,the solute concentrations on the SF plane and their configurations were adjusted to be the same as in their references.The Mg–Al–Ca alloy and its sub-binary alloys had the same solute concentrations and configurations as those in Hase et al.[95]whose solute concentration on the SF planes is 11.1 at% for the basal sample,16.7 at% for the prismatic and pyramidal I samples,and 25.0 at% for the pyramidal II sample.The reference of the Mg–Al–Zn alloy and its subbinary alloys was Wang et al.[96]whose solute concentration on the SF planes is 16.7 at% for the basal and pyramidal II samples,and 8.3 at% for the prismatic and pyramidal I samples.The detailed calculation procedure is described in our previous works[27,28].The calculated GSFE curves for the slip planes of each ternary Mg alloy are shown in Fig.5 along with those of its sub-binary Mg alloys and pure Mg.To confirm the reliability of the present GSFE calculations,we compared the stable and unstable SF energy(SFEs)of the calculated GSFEs with first-principles calculations[95–99](Table 10 and Table 11).Although the SFEs between the calculations are not identical,the presently calculated SFEs show an alloying effect similar to the first-principles calculations[95–99].The similarity is higher than that between the other MEAM calculation[22]and the first-principles calculations[95–99].In particular,the effect of Zn on the GSFE of Mg is better reproduced with the present potential than with the other MEAM potential[22].This is due to the Mg–Zn potential used in the present development reproducing the GSFE well[28].

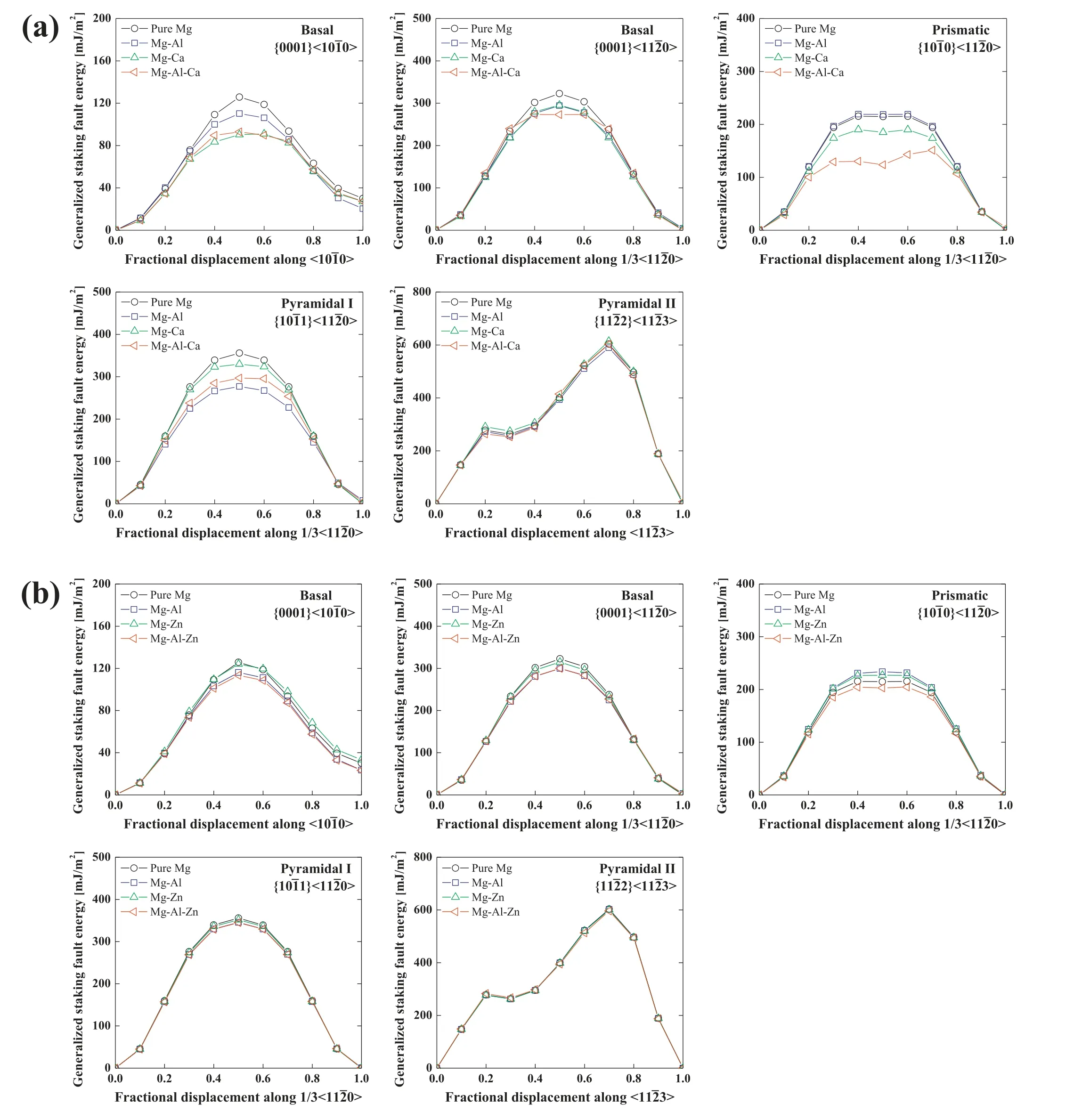
Fig.5.Calculated GSFE(mJ/m2)curves of pure Mg,Mg–Al,Mg–Ca,Mg–Zn,Mg–Al–Ca and Mg–Al–Zn models for the basal,prismatic,pyramidal I,and pyramidal II slip systems,using the present 2NN MEAM potentials.The solute concentrations on the SF plane and their configurations in the Mg–Al,Mg–Ca and Mg–Al–Ca models are the same as in reference[95],while those in the Mg–Al,Mg–Zn,and Mg–Al–Zn models are the same as in reference[96].

The applicability to the recrystallization behavior was confirmed by calculating the segregation energy of Al,Ca,and Znsolutes on GBs of Mg.The calculation was conducted for an hcp bicrystal sample containing a GB.The types of GB were{10¯12}and{10¯11}twin boundaries(TBs).The sample size of the{10¯12}TB was 12nm×3nm×3nm consisting of 4800 atoms and that of the{10¯11}TB was 9nm×5nm×3nm consisting of 5756 atoms.For these samples,the segregation energy was calculated by subtracting the energy when a solute atom is located in the matrix from the energy when the atom is located on GB.The detailed calculation procedure is described in our previous work[23].As shown in Fig.6,there are many segregation sites for a solute atom on the GB,and each segregation site has different segregation energy.Among these sites,we chose the most stable segregation site,which had the most negative segregation energy,and listed the calculated energy in Table 12.According to the present calculation,the most stable segregation sites of Al and Zn are the compression sites(site C in Fig.6)and that of Ca is the extension site(site E in Fig.6),in both binary and ternary Mg alloys.This is due to the atomic sizes of Al and Zn being smaller than Mg,but that of Ca being larger than Mg.The calculated segregation energy of the binary models is in reasonable agreement with first-principles calculations[9,100–102].On both TBs,the segregation energy in the Mg–Al–Ca model is more negative than the summation of the energy in the Mg–Al and Mg–Ca models,while the energy in the Mg–Al–Zn model is the same as the summation of the energy in the Mg–Al and Mg–Zn models.The difference arises from the size difference between two solute atoms.The most stable segregation sites of Al and Ca are the compression and extension sites,respectively.In addition,they are adjacent,as illustrated in Fig.6.As a result,the compressive volumetric strain(due to the atomic size of Al smaller than Mg)could offset the tensile volumetric strain(due to the atomic size of Ca larger than Mg).This offset would make the co-segregation of Al and Ca more stable.On the other hand,since the most stable segregation sites of Al and Zn are the compression sites,the volumetric strain cannot be offset.The above phenomenon that the co-segregation becomes more stable in the Mg–Al–Ca model is also reported to occur in a Mg–Zn–Ca model containing Zn(its atomic size is smaller than Mg)and Ca(its atomic size is larger than Mg)[23].It should be mentioned here that recrystallization mech-anisms are too complex to be elucidated by MD simulation only.Godiksen et al.had attempted to investigate the inhomogeneous interactions between migrating GBs and dislocations during recrystallization using MD simulations[103,104].They observed the rearrangement and annihilation of dislocations,and found that the nature of the migration process is not homogeneous and the dislocation-driven boundary migration depends on the types of dislocations and grain boundaries,but their results are rather insufficient to explain all the recrystallization behaviors.However,the information obtained from the MD simulations are valuable and can be utilized for future studies.Likewise,MD simulations can compensate some part that experimental and theoretical approaches cannot handle since those simulations can analyze the kinetic behaviors of materials in atom-scale,thereby enabling to provide some key factors of understanding the recrystallization mechanisms.Grain boundary segregation is the above part that MD simulations can contribute,and simultaneously plays an im-portant role in recrystallization behaviors in alloys.For these reasons,we are willing to investigate the segregation behavior using MD simulations to understand the recrystallization of Mg alloys more clearly,and thus we first confirmed the transferability of the presently developed potentials for the segregation energy.

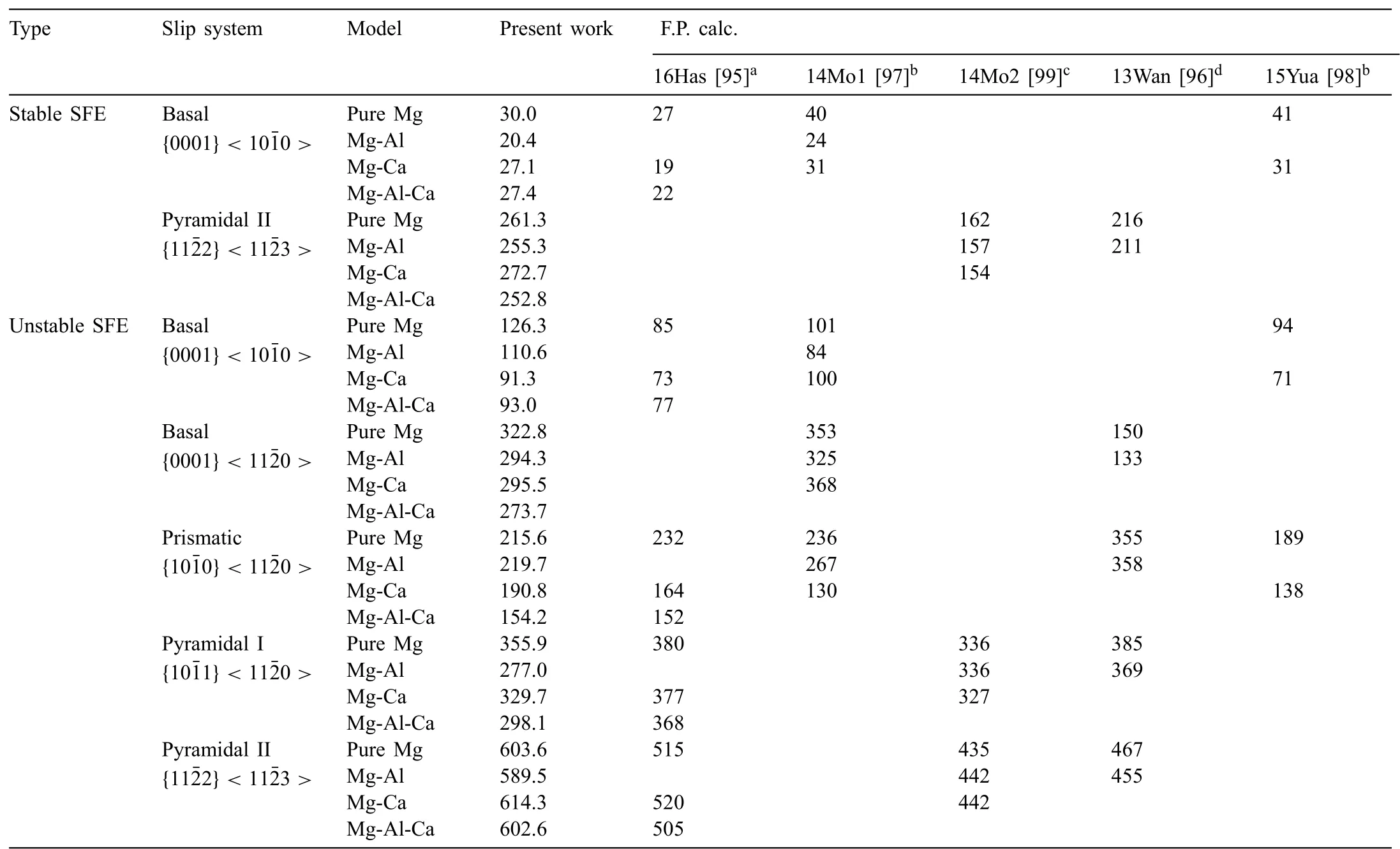
Table 10Calculated stable and unstable SFE(mJ/m2)of pure Mg,Mg–Al,Mg–Ca,and Mg–Al–Ca models for the basal,prismatic,pyramidal I,and pyramidal II slip systems,using the present 2NN MEAM potentials,in comparison with literature data.The solute concentrations on the SF plane and their configurations in the present work are the same as in reference[95](which is denoteda).

Table 11Calculated stable and unstable SFE(mJ/m2)of pure Mg,Mg–Al,Mg–Zn,and Mg–Al–Zn models for the basal,prismatic,pyramidal I,and pyramidal II slip systems,using the present 2NN MEAM potentials,in comparison with literature data.The solute concentrations on the SF plane and their configurations in the present work are the same as in reference[96](which is denoted a).

Table 12Calculated solute segregation energy(eV)in Mg–Al,Mg–Ca,Mg–Zn,Mg–Al–Ca and Mg–Al–Zn models on{102}and{101}TBs using the present 2NN MEAM potentials,in comparison with first-principles calculations.The segregation sites of Al and Zn are the compression sites(site C in Fig.6)and that of Ca is the extension site(site E in Fig.6)in the present work and first-principles calculations.

Table 12Calculated solute segregation energy(eV)in Mg–Al,Mg–Ca,Mg–Zn,Mg–Al–Ca and Mg–Al–Zn models on{102}and{101}TBs using the present 2NN MEAM potentials,in comparison with first-principles calculations.The segregation sites of Al and Zn are the compression sites(site C in Fig.6)and that of Ca is the extension site(site E in Fig.6)in the present work and first-principles calculations.

Model {10¯12}twin boundary {10¯11}twin boundary Present work F.P.calc. Present work F.P.calc.Mg–Al −0.25 −0.16[100],−0.24[101] −0.23 −0.14[100],−0.11[102]Mg–Ca −0.27 −0.30[100] −0.22 −0.26[100],−0.12[102]Mg–Zn −0.20 −0.22[9],−0.23[100],−0.26[101] −0.15 −0.22[100],−0.11[102]Mg–Al–Ca −0.58 −0.50 Mg–Al–Zn −0.45 −0.38

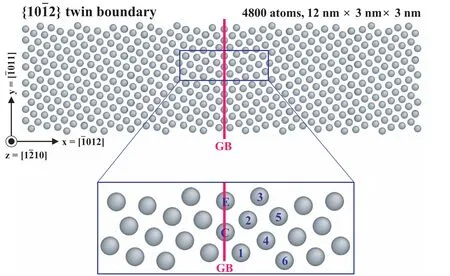
Fig.6.Atomic configuration in a GB sample,containing a{10¯12}TB in the middle of the sample[23].The lattice sites labeled E and C mark extension and compression segregation site,respectively.The lattice sites labeled 1 through 6 mark various possible segregation sites.

Table 13Calculated thermal expansion coefficientsε(10−6/K)of stable MgxAly,MgxCay,MgxZny,AlxCay,MgxAlyCaz and MgxAlyZnz intermetallic compounds using the present 2NN MEAM potentials,in comparison with experimental data and first-principles calculations.

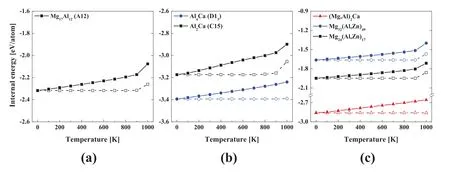
Fig.7.Change in the internal energy of stable(a)MgxAly and(b)AlxCay binary,and(c)MgxAlyCaz and MgxAlyZz ternary compounds with increasing temperature(filled symbols)and rapid cooling to 0K from each heating temperature(open symbols).

The presently developed Mg–Al–Ca and Mg–Al–Zn potentials can reproduce structural and thermodynamic properties of ternary compounds as well as the binding energy of Al–Ca and Al–Zn solute pairs in the Mg matrix,the GSFE on basal and non-basal slip planes,and the segregation energy on TBs of the Mg–Al–Ca and Mg–Al–Zn alloys.Despite the good performance at 0K properties,for robust applicability,the reliability of the developed potentials should also be confirmed in the general processing temperature range of Mg alloys:298–723K[3–5,10].The reliability was investigated by checking whether the stable MgxAly,MgxCay,MgxZnyand AlxCaybinary and MgxAlyCazand MgxAlyZnzternary compounds have an appropriate thermal expansion coefficient and can maintain their crystal structures at finite temperatures.The thermal expansion coefficients were calculated using the velocity Verlet algorithm and the Parrinello/Rahman NPT ensemble in the temperature range of 273–373K,considering that comparable literature data are mainly calculated around 300K[57,105–107].The compound samples consisted of 500–2000 atoms.The calculation results are presented in Table 13 in comparison with literature data.The present calculation for the Mg17Al12compounds is in reasonable agreement with the first-principles calculation[105].That of the Mg2Ca compound is a little smaller than the first-principles calculations[57,106,107],and those of the MgZn2and Al2Ca compounds are larger than the first-principles calculations[57,107–109];Despite of the discrepancy,the present calculations are comparable with the first-principles calculations.The other compounds could not be compared due to the lack of comparable literature data,but show similar values to the compounds confirmed.In the case of crystal structure maintenance,we previously confirmed that those of the MgxCayand MgxZnybinary compounds are maintained up to 1000K[23]and 900K[28],respectively.Thus,in this study,we examined the finite temperature structural stability of the MgxAlyand AlxCaybinary and the MgxAlyCazand MgxAlyZnzternary compounds.For this examination,each compound sample was incrementally heated up to 1000K,and rapidly cooled to 0K from each heating temperature.The cooled structure was then compared with its original crystal structure.The compound samples consisted of around 2000 atoms.The heating interval was 100K,and the equilibration time at each heating temperature was 30ps.Fig.7 shows the internal energy of these compounds after heating to and cooling from each heating temperature.The standard deviation values of the calculated internal energy are listed in Table S2.In the case of the Mg17Al12,Al4Ca,Mg32(Al,Zn)49,and Mg24(Al,Zn)17compounds,the internal energy increases monotonically with heating up to 900K and recovers the initial 0K energy after cooling.The Al2Ca and(Mg,Al)2Ca compounds show the same trend until the heating temperature reaches 700K and 800K,respectively.These results indicate that all stable compounds composing the Mg–Al–Ca and Mg–Al–Zn ternary systems present reasonable thermal expansion coefficients at RT and are thermally stable in the processing temperature range.Therefore,the presently developed Mg–Al–Ca and Mg–Al–Zn interatomic potentials can be utilized for studying deformation and recrystallization behaviors of the Mg–Al–Ca and Mg–Al–Zn alloys and commercial higher-order Mg alloys within the entire range of processing temperature.

4.Conclusion

In the present work,interatomic potentials for the Al–Ca and Al–Zn binary and the Mg–Al–Ca and Mg–Al–Zn ternary systems were developed based on the 2NN MEAM formalism.The developed potentials well describe the structural,elastic,and thermodynamic properties of compounds and solutions in the relevant systems.The ternary potentials reproduce the binding energy of Al–Ca and Al–Zn solute pairs in Mg matrix,the GSFE on the basal and non-basal slip planes,and the segregation energy on TBs in the Mg-rich hcp Mg–Al–Ca and Mg–Al–Zn alloys,in reasonable agreement with first-principles calculations.The stable compounds composing the Mg–Al–Ca and Mg–Al–Zn ternary systems have a reasonable thermal expansion coefficient around RT and are thermally stable in the processing temperature range.These potentials can be extended to commercial multicomponent Mg alloy systems in combination with previously developed 2NN MEAM potentials for other binary and ternary Mg alloy systems,contributing to an understanding of the deformation and recrystallization behaviors at an atomic scale and to the computational design of new Mg alloys with improved RT formability.

Acknowledgments

This research has been financially supported by the Nano•Material Technology Development Program(2016M3A7B4024132)and the Basic Science Research Program(2016R1A2B4006680)through the National Research Foundation of Korea(NRF)funded by the Ministry of Science & ICT.

Supplementary materials

Supplementary material associated with this article can be found,in the online version,at doi:10.1016/j.jma.2020.09.006.

Appendix A

The detailed formalism of the(2NN)MEAM is from the literatures[29,36,40].It has been shown in Eq.(1)that the energy in the MEAM is composed of two terms,the embedding function term and the pair interaction term.The embedding function is given the following form[38],

where A is an adjustable parameter,Ecis the cohesive energy andis the background electron density for a reference structure.The reference structure is a structure where individual atoms are on the exact lattice points.Normally,the equilibrium structure is taken as the reference structure for elements.The background electron densityis composed of spherically symmetric partial electron density,and angular contributions,Each partial electron density term has the following form[38,110],

where

whereρ0is a scaling factor,β(h)are adjustable parameters and reis the nearest-neighbor distance in the equilibrium reference structure.The scaling factor doesn’t give any effect on calculations for elements,but can give effect on calculations for alloy systems.

In the MEAM no specific functional expression is given directly toφ(R).Instead,the atomic energy(total energy per atom)is evaluated by some means as a function of nearestneighbor distance.Then,the value ofφ(R)is computed from known values of the total energy and the embedding energy,as a function of nearest-neighbor distance.

Let’s consider a reference structure once again.Here,every atom has the same environment and the same energy.If up to second nearest-neighbor interactions are considered as is done in the 2NN MEAM[29,36],the total energy per atom in a reference structure can be written as follows:

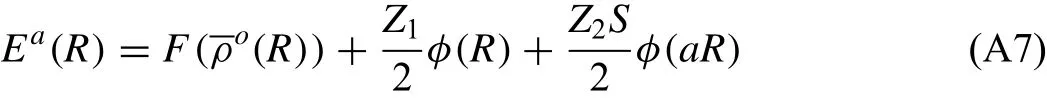
where Z1and Z2are the number of first and second nearestneighbor atoms,respectively.S is the screening factor for second nearest-neighbor interactions(the screening factor for first nearest-neighbor interactions is 1),and a is the ratio between the second and first nearest-neighbor distances.It should be noted that for a given reference structure S and a are constants,and the total energy and the embedding energy become functions of only nearest-neighbor distance R.On the other hand,the energy per atom for a reference structure can be obtained from the zero-temperature universal equation of state of Rose et al.[37]as a function of nearest-neighbor distance R.

Eu(R)is the universal function for a uniform expansion or contraction in the reference structure,B is the bulk modulus andΩis the equilibrium atomic volume.

Basically,the pair potential between two atoms separated by a distance R,φ(R),can be obtained by equating Eq.(A7)and Eq.(A8).However,it is not trivial because Eq.(A7)contains two pair potential terms.In order to derive an expression for the pair interaction,φ(R),another pair potential,ψ(R),is introduced:

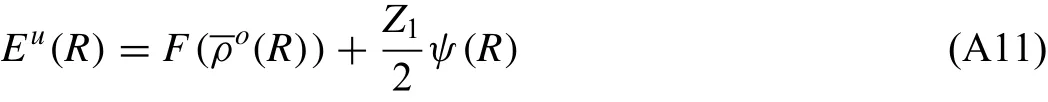
where

ψ(R)can be computed from Eq.(A11)as a function of R,as follows:

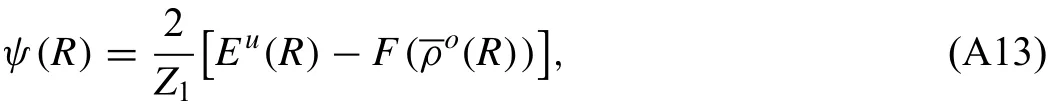
and the expression for the pair potentialφ(R)is obtained from Eq.(A12)as follows:

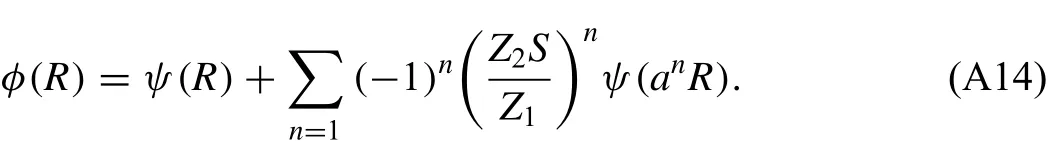
Here,the summation is performed until a correct value of atomic energy is obtained for the equilibrium reference structure.

To describe a binary alloy system,in addition to the descriptions for individual elements,the pair interaction between different elements should be determined.For this,a similar technique used to determine the pair interaction for pure elements is applied.A perfectly ordered binary intermetallic compound,where one type of atom has only same type of atoms as second nearest-neighbors,is considered as a reference structure.The Bl(NaCl type)or B2(CsCl type)ordered structure can be a good example.For such a reference structure,the total energy per atoms(for l/2 i atom+1/2 j atom)is given as follows:

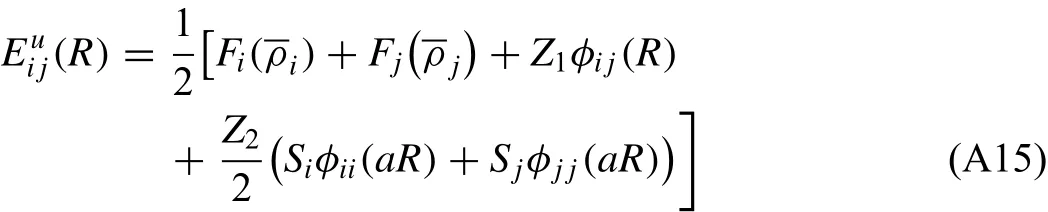
where Z1and Z2are the numbers of first and second nearestneighbors in the reference structure,respectively.Siand Sjare the screening functions for the second nearest-neighbor interactions between i atoms and between j atoms,respectively,and a is the ratio between the second and first nearestneighbor distances in the reference structure.The pair interaction between i and j can now be obtained in the following form:

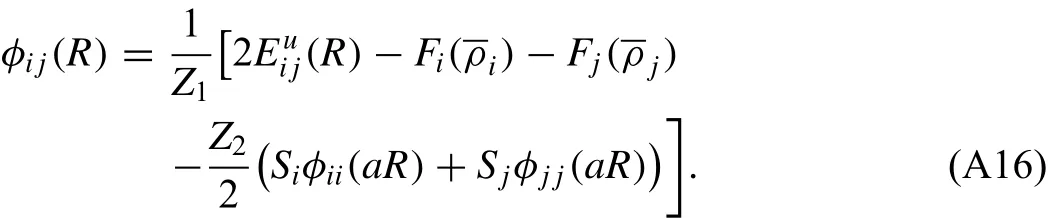
The embedding functions Fiand Fjcan be readily computed.The pair interactionsφiiandφjjbetween the same types of atoms can also be computed from descriptions of individual elements.To obtainthe universal equation of state,Eqs.(A8)–(A10),is considered once again for the binary reference structure.In this case,Ec,reand B correspond to the cohesive energy,equilibrium nearest-neighbor distance and bulk modulus of the binary reference structure.

In addition to the parameters for the universal equation of state,two more model parameter groups,Cminand Cmax,must be determined to describe alloy systems.Each element has its own value of Cminand Cmax.Cminand Cmaxdetermine the extent of screening of an atom(k)to the interaction between two neighboring atoms(i and j).For pure elements,the three atoms are all the same type(i-j-k=A-A-A or B-B-B).However,in the case of binary alloys,one of the interacting atoms and/or the screening atoms can be different types(there are four cases:i-k-j=A-B-A,B-A-B,A-A-B and A-B-B).Different Cminand Cmaxvalues may have to be given in each case.Another,the last model parameter necessary for binary alloy systems is the atomic electron density scaling factorρo(see Eq.(A6)).For an equilibrium reference structure(R=re),the values of all atomic electron densities becomeρo.This is an arbitrary value and does not have any effect on calculations for pure elements.This parameter is often omitted when describing the potential model for pure elements.However,for alloy systems,especially for systems where the constituent elements have different coordination numbers,the scaling factor(the ratio of the two values)has a great effect on calculations.