The effect of the 18R-LPSO phase on the fatigue behavior of extruded Mg/LPSO two-phase alloy through a comparative experimental-numerical study

Fbien Briffod,Tkyuki Shiriw,Mnbu Enoki

Department of Materials Engineering,The University of Tokyo,7-3-1 Hongo,Bunkyo-ku,Tokyo 113–8656,Japan

Received 14 May 2020;received in revised form 10 July 2020;accepted 28 July 2020

Available online 25 September 2020

Abstract The fatigue behavior of four extruded Mg-Y-Zn alloys containing different volume fractions of long-period stacking ordered(LPSO)grains was investigated through a comparative study combining experiments and crystal plasticity finite element simulations.Strain controlled low-cycle fatigue experiments were conducted at different strain amplitudes and revealed a limited cyclic hardening in Mg89Zn4Y7 alloy or softening in Mg99.2Zn0.2Y0.6 and Mg97Zn1Y2 alloys.A decrease in the fatigue life against the plastic strain with the increase in LPSO phase volume fraction was observed and was related the limited ductility of extruded LPSO grains.Stress-strain hysteresis curves were used to calibrate and validate a crystal plasticity model taking into account twinning and detwinning.The interaction of the different phases on the distribution of local micro-mechanical fields at the grain scale was then analyzed on synthetic microstructures under strain-controlled conditions.Deformation twinning activity was predicted in coarse unrecrystallized grains and tended to disappear with the increase in the LPSO phase volume fraction.Cleavage-like facets observed in LPSO grains were related to high tensile stress,especially at the Mg/LPSO interface,due to the limited number of deformation mechanisms in LPSO crystal to accommodate out-of-basal plane strain.The increase of the fatigue limit with the increase in LPSO phase volume fraction was finally associated with the decreasing presence of coarse unrecrystallized α-Mg grains due to a higher dynamic recrystallization activity during the extrusion process.

Keywords:Magnesium alloy;Fatigue;Long-period stacking ordered phase;Crystal plasticity;Finite element method.∗Corresponding author.

1.Introduction

The increasing need for energy saving pushes transport industries towards weight reduction strategies notably by replacing high density materials such as steels with lower ones.In this regard,magnesium(Mg)and Mg alloys are receiving particular attention in the past decades as they present the lowest densities among structural metals and may be easily recycled[1].However,their relatively poor strengths and strong mechanical anisotropies related to the low-symmetry of the hexagonal closed packed(hcp)crystal structure and significant strength discrepancy of the different deformation modes often limit their application to non-structural parts.In particular,the ease of activating mechanical twinning to accommodate out-of-basal plane deformation results in a tensioncompression yield asymmetry in extruded Mg alloys with strong texture.Combined with the low strength of basal slip,it generally leads to poor long-term fatigue performances for most conventional Mg alloys compared to other metal families[2].

A recent strategy to inhibit the activation of deformation twinning and improve the strength of dislocation slip is related to the introduction of rare-earth(RE)elements in the chemical composition,notably Gd,Y and Zr elements[3–6].Their presence tends to promote the formation of fine-grained microstructures having a weaker crystallographic texture,through dynamic recrystallization during the thermo-mechanical process[7].Consequently,the appearance of extension twins are greatly hindered as their formation is highly grain size dependent.The presence of solute RE elements also increases the dislocation slip strength by impeding dislocation motion through solid solution strengthening and precipitation hardening.As a result,Mg-RE alloys tend to exhibit better strength and fatigue performances than commercial Mg alloys.Among them,ternary Mg-Zn-Y alloys containing long-period stacking ordered(LPSO)phase have received extensive attention due to their outstanding strength and creep resistance even at elevated temperature[8–10].LPSO phases are crystals sharing the same(0001)basal plane than hcpα-Mg but whose stacking sequence along the c-axis is extended to 10,14,18 or up to 24-fold through an alternating stacking of fcc and hcp layers[11,12].While,ascast Mg/LPSO two-phase alloys do not present significantly higher strength than conventional Mg alloys,it is substantially improved by the extrusion process[13].Indeed,due to the low-symmetry of the LPSO crystal structure,the plastic deformation is highly anisotropic and the(0001)〈11¯20〉basal slip system is the only available deformation mode[14].However,when subjected to compressive load perpendicular to the c-axis,LPSO crystal may deform by kink band formation[15]in a similar way than in zinc or cadmium single crystals[16].In this regard,the extrusion process generates fiber-shaped LPSO grains elongated along the extrusion direction(ED)with their c-axis perpendicular to the ED and containing a large proportion of kink boundary[17].The increasing presence of kink boundaries with the extrusion ratio associated with the drastic increase in the flow stress suggested that they may act as additional strengthening mechanisms by impeding basal dislocation motion[13].The much higher elastic stiffness of LPSO crystal compared with theα-Mg one,especially along the c-axis[18],may also contribute to fiber reinforcement in a same way than in composite structures[17].

As a consequence,while as-cast Mg–Y–Zn alloys showed similar fatigue performances to commercial Mg alloys under positive mean stress,it was greatly improved by the extrusion process[19].To clarify the effect of LPSO volume fraction,both low-cycle and high-cycle fatigue experiments were conducted on extruded Mg/LPSO having two different volume fraction[20].An increase in the cyclic strength with the increase in the LPSO phase volume fraction was observed in conjunction with limited cyclic hardening/softening.Fracture surface analysis revealed a shift from cleavage-like faceting initiation in LPSO grains to crack initiation fromα-Mg when transitioning from low-cycle to high-cycle fatigue.A slight improvement in the fatigue limit was noted with the increase in the LPSO phase volume fraction,but the fatigue lives were relatively close due to similar crack propagation lives.However,the contributions of the individual phases on the fatigue response of the Mg/LPSO two-phase alloys is still unclear due to the difficulty to assess the local micro-mechanical fields during fatigue experiments.

Non-destructive experimental techniques,such as the acoustic emission(AE)method combined with X-ray diffraction analysis were found successful to elucidate the local plastic deformation modes occurring during compression tests of Mg/LPSO two-phase alloys[21].Alternatively,numerical methods,especially the finite element method(FEM)has become a popular approach to elucidate the individual contribution of each phase on the mechanical response of a multiphase materials.In the case of multi-phase metal,the constitutive behavior is generally reproduced through crystal plasticity models that take into account the local crystal orientations and the available deformation mechanisms of each phase.At the difference of mean-field schemes,such as the Taylor model or more recently the visco-plastic self-consistent(VSPC)models often used for the texture evolution prediction in the case of Mg alloys[22–25],the crystal plasticity FEM(CPFEM)is capable of predicting the heterogeneity of the local fields at the grain scale and the effect of the spatial distribution of the different constituents on the local stress and strain partitioning.

We therefore propose a study in which the fatigue properties of Mg/LPSO two-phase alloys are analyzed in view of the individual properties of its constituent both experimentally and numerically.Strain-controlled and load-controlled fatigue experiments are therefore carried out on extruded Mg and 18R-LPSO alloys separately.These results are then used to elucidate the fatigue behavior of Mg/LPSO two-phase alloys through a comparison with previous experimental work[20]and CPFE simulations of synthetic microstructures.In this regard,a numerical procedure based on a multi-scale anisotropic tessellation is proposed to generate synthetic polycrystals representative of the investigated materials.

2.Materials and methods

2.1.Materials and experimental methods

Four Mg–Zn–Y alloys with varying compositions were investigated in the present study:Mg99.2Zn0.2Y0.6,Mg97Zn1Y2,Mg89Zn4Y7and Mg85Zn6Y9(atomic fraction,%).They were produced from high-frequency induction melting and carbon crucible casting from high purity constitutive metals(99.9%).The ingots were then hot-extruded at 450◦C,with an extrusion ratio of 10 to 1 and an extrusion speed of 2.5 mm/s,leading to round bars of 8 mm diameter.

The obtained microstructures were investigated by optical microscope,scanning electron microscope(SEM)and electron-backscattered diffraction(EBSD)analysis on a longitudinal section along the extrusion direction(ED).Despite knowing the theoretical diffraction pattern of the 18R-LPSO,the crystal orientation of the LPSO phase could not be estimated so that no EBSD measurement was obtained for the Mg85Zn6Y9alloy.In addition,LPSO regions in other alloys appeared as unindexed regions.

To clarify,the individual effect of theα-Mg phase and the LPSO-phase on the cyclic properties of Mg/LPSO two-phase alloys,fully reversed strain-controlled low-cycle and loadcontrolled high-cycle fatigue experiments were conducted in both materials at different amplitudes.These experiments were already carried out for Mg97Zn1Y2and Mg89Zn4Y7two-phase alloys in previous study[20]and some results will be reported here again for comparison purpose.Similar specimens and conditions were used than in previous study and the reader is referred to it for additional information[20].

2.2.Numerical methods

2.2.1.Constitutive model

A phenomenological crystal plasticity model including dislocation slip,deformation twinning and subsequent slip in twinned region presented in previous studies[26,27]was used in this work.It was implemented as a user material subroutine(UMAT)for the FEM software Abaqus.The main constitutive equations are briefly summarized hereafter.Additional information regarding the modeling hypotheses can be found in past works[26,27].

Following the multiplicative decomposition of the deformation gradient F into an elastic stretching Feand an incompressible plastic contribution Fp,the plastic velocity gradient Lpis divided into two expressions based on the total twin volume fractionwithin a material point:

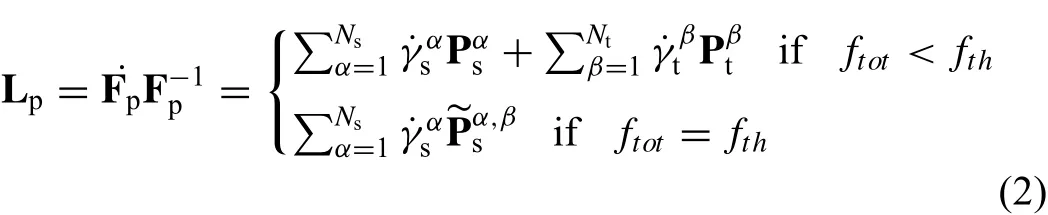
where C and Cβare the elasticity tensors of the matrix and twin variantβ,respectively.Additionally,once the twin volume fraction threshold is reached,only the stiffness tensor of the predominant twin variant is considered.

The slip shear rate is described by a viscous-type power law equation:

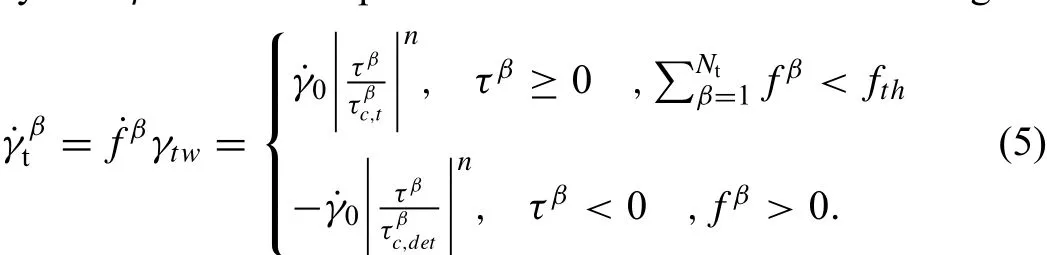
whereγtwis the reference twin strain,aredetwinning,resp

the shear resistances for twinning and ectively.Strain-controlled cyclic tests on extruded Mg97Zn1Y2and Mg89Zn4Y7alloy did not exhibit significant cyclic strainhardening[17,20].Accordingly,no evolution of the shear resistances was considered in this work for both theα-Mg and LPSO phases.However,size effect is an important parameter that should be considered as the considered microstructures are very heterogeneous with DRXed grains much smaller than the unDRXed ones.In this regard,a Hall–Petch type relationship was considered in this work:

where dgis the equivalent grain size and kα/βis the Hall–Petch parameter for the slip or twin systemαorβ.Extensive reviews on the Hall–Petch relationship in Mg alloys revealed that it strongly depends on the loading type(tension,compression)and the crystallographic texture as different deformation deformation mechanisms may be activated[30–32].In particular there is significant scattering of the Hall–Petch parameter even for similar materials[33].Alternatively,a theoretical expression is often used for estimating the parameter[34–36]and is given by:

whereνis the Poisson ratio,G the shear modulus,τ∗the barrier strength and bαthe burger’s vector of the deformation systemα.The barrier strength is often taken to be a ratio of the shear modulus,τ∗=0.01G[34–36].However,a numerical application of Eq.(7)shows significant discrepancy with the experimental estimations[33].Accordingly,it was decided to consider an experimental Hall–Petch parameter for the basal/prismatic dislocation slip and estimate the other parameters based on the ratio of the burger’s vector using Eq.(7).The Hall–Petch parameter for basal/prismatic slip was taken from the work of Razavi et al.[37]as the investigated grain sizes were close to that in our current study and equal to 150 MPa.μm1/2.In the case of the LPSO grains,no Hall–Petch relationship was considered due to lack of experimental data and since the relevant length scale parameter in the case of an extruded LPSO grain may be attributed to the average distance between kink boundaries which can be inferred to be uniform from one grain to the other.

Due to the low symmetry of the LPSO crystal structure only basal slip is considered as an available slip system.Onthe other hand,three(0001)〈11¯20〉basal,three{1¯100}〈11¯20〉prismatic and six{10¯11}〈11¯20〉pyramidal-2 slip systems as well as the six{10¯12}〈10¯11〉extension twin systems are considered for theα-Mg crystal.The elastic stiffness components of theα-Mg and LPSO crystals were taken from literature[18,35]and are summarized in Table 1 assuming transverse isotropic properties for the LPSO phase.

Table 1Elastic stiffness components ofα-Mg and LPSO crystals.

Fig.1.(a)Example of a periodic ellipse sampling process(b)generated microstructure after the first scale tessellation,(c)microstructure after the second scale tessellation to reproduce the recrystallization process,(d)crystallographic orientation attribution and(e)conformal meshing respecting grain boundaries.

2.2.2.Microstructure modeling

The modeling of synthetic two-dimensional multi-phase microstructures is based on a developed multi-scale anisotropic tessellation procedure previously developed in the case of ferritic and martensitic steels[38–40].The fundamental steps of the proposed method are depicted in Fig.1 and detailed hereafter.

From the EBSD analysis of the investigated materials,three groups of grains should be considered:thin and elongated LPSO grains,large and highly deformedα-Mg un-DRXed grains,and smallα-Mg equiaxed DRXed grains.Key parameters used to statistically quantify the microstructure are the grain morphologies,their crystal orientations and the volume fraction of each constituent group.The grain morphology descriptors are based on an ellipse fitting procedure where each grain was described in terms of major axis,aspect ratio and relative orientation.The crystallographic texture was estimated separately for DRXed and unDRXed grains based on the orientation distribution function(ODF).

To control the morphological and spatial distribution of grains and phases,in particular the distribution of DRXed grains,a two-scale anisotropic tessellation was conducted.The first scale tesselation takes as input the domain of randomly positioned ellipses(Fig.1(a))sampled from the empirical statistical distributions estimated from the EBSD measurements.To ensure the spatial periodicity of the resulting tessellation,ellipses crossing the edges of the domain were extended through the opposite edge.A first scale anisotropic tessellation was then applied to generate the grain boundaries(Fig.1(b)).Additional ellipses sampled from the statistical distributions of DRXed grains are positioned within each grain that should undergo recrystallization(DRXed Mg prior).Lower-scale tessellations are then performed in these domains to generate the grain boundaries of the small DRXed grains(Fig.1(c)).Since LPSO ellipses are positioned first in the procedure,it restricts the size of unDRXed grains as seen experimentally when the volume fraction of LPSO phase increases.In addition,the two-scale procedure prevents DRXed grains to be randomly scattered in the microstructure as they restrict them to belong to a given prior un-DRXed grain which is phenomenologically coherent with the principle of recrystallization.In the final step,a crystal orientation is attributed to each grain based on the experimental ODF and an algorithm taking into account the grain size[41].

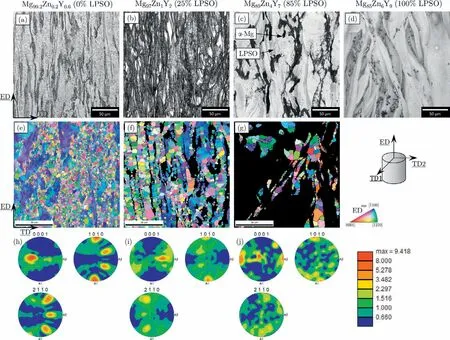
Fig.2.(a-d)Optical micrographs,(e-g)EBSD maps with IPF color coding and(h-j)corresponding pole figures of extruded(a,e,h)Mg99.2Zn0.2Y0.6,(b,f,i)Mg97Zn1Y2,(c,g,j)Mg89Zn4Y7 and(d)Mg85Zn6Y9 alloy.

The following procedure was applied to the modeling of the four investigated materials.In each case,ten fully-periodic synthetic microstructures of dimension 100×100μm were generated.The same distributions were used for all the materials so that the only varying parameter was the volume fraction of the LPSO-phase.unDRXed grains were set to account for 30% of theα-Mg grains in the 0% LPSOphase microstructures and 11% of theα-Mg grains in the 25% and 85% LPSO phase microstructures.These proportions were roughly estimated from EBSD measurements.The microstructures were meshed with about 50,000 C3D6 wedge elements with one element in the thickness.Fig.1(e)shows an example of the meshed microstructure.Periodic boundary conditions were applied on each face and the models were loaded either under strain-controlled or load-controlled conditions to simulate either low-cycle or high-cycle fatigue behavior.

3.Results and discussion

3.1.Microstructure analysis

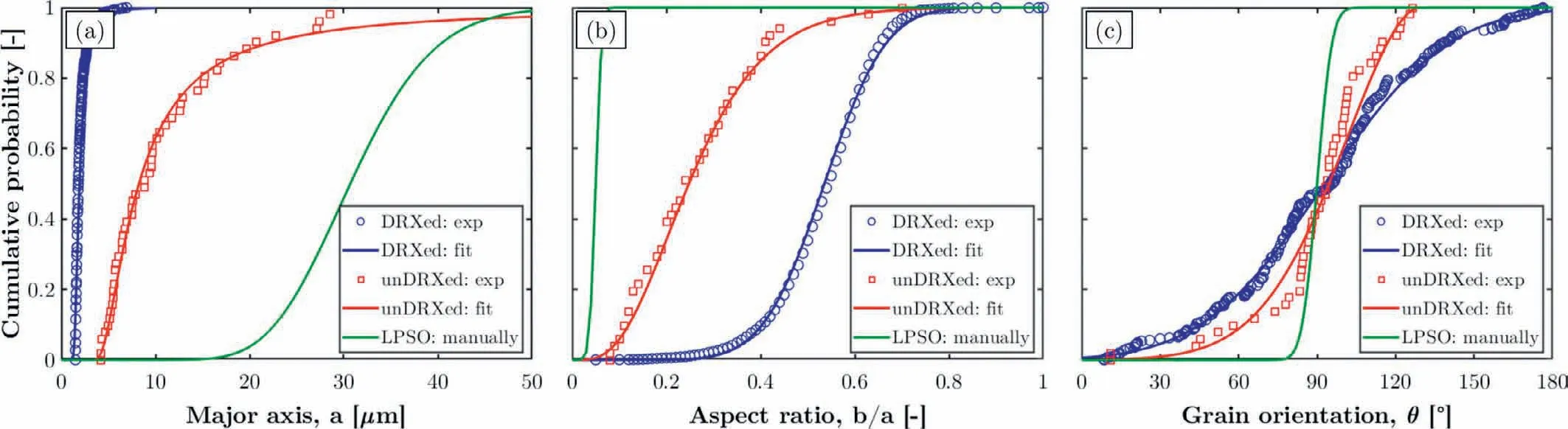
Fig.3.Experimental and fitted cumulative distribution functions of(a)the grain major axis,(b)the grain aspect ratio and(c)the grain orientation estimated from an ellipse fitting of the DRXed and unDRXed grains of the Mg99.2Zn0.2Y0.6 alloy.The distributions for LPSO grains were manually determined to reproduce the elongated needle-like structure from the work of Hagihara et al.[9].

Fig.2(a–d)shows optical micrographs of the four investigated materials.Due to different polishing conditions,α-Mg grains appear in white in Mg99.2Zn0.2Y0.6alloy and in black in others.It is observed that with the increase in LPSO-phase volume fraction,the size of LPSO grains tend to increase as well.Small particles at the surfaces of Mg85Zn6Y9were found to correspond to pure yttrium.Fig.2(e–g)represents the inverse pole figure(IPF)maps of the three materials containingα-Mg grains and Fig.2(h–j)shows their corresponding pole figures.Unindexed regions in black correspond to the LPSO phase.Fig.2(d)depicts SEM micrograph of the Mg85Zn6Y9alloy.The materials contain about 0%,25%,85%and 100% LPSO grains for the Mg99.2Zn0.2Y0.6,Mg97Zn1Y2,Mg89Zn4Y7and Mg85Zn6Y9alloys,respectively.It should be pointed out that the chemical composition of Mg99.2Zn0.2Y0.6alloy was selected as it corresponded to the composition of α-Mg grains in other alloys[17].α-Mg grains in the three EBSD map exhibit a bi-modal distribution with coarse unrecrystallized and highly deformed grains(unDRXed)and finely refined dynamically recrystallized grains(DRXed).UnDRXed grains represented about 30%,10% and 2% ofα-Mg grains in Mg99.2Zn0.2Y0.6,Mg97Zn1Y2and Mg89Zn4Y7,respectively.The increased grain refinement proportion was associated with the presence of the LPSO-phase generating stress concentration at the interface,thus acting as specific sites promoting the recrystallization process[17].LPSO-phase appeared as thin band elongated along the ED and containing a large number of kink boundaries due to the extrusion process as shown in other studies[13,42].Texture analysis revealed relatively strong texture in both materials,characterized by a(0001)basal peak perpendicular to the ED,characteristic of the extrusion process.This texture is particularly strong for unDRXed grains as observed in Mg99.2Zn0.2Y0.6alloy.It was finally inferred that the LPSO-phase also exhibit a basal texture based on the work of Hagihara et al.[42].

Fig.3 depicts the empirical and fitted cumulative distributions of the three descriptors used to quantify the grain morphologies.They were estimated from the EBSD data of Mg99.2Zn0.2Y0.6alloy.Due to the poor indexing of the LPSO phase grains(black regions in Fig.2),a clear measurement of both the grains geometry and crystal orientation were impossible from the EBSD measurements.Therefore,the crystal texture of the LPSO phase was assumed to be similar to that of the unDRXed grains and the grain shape distributions were manually estimated so that the generated microstructures were relatively close to that of Fig.2(b–d)and from the work of Hagihara et al.[9,42].

3.2.Low-cycle fatigue behavior

3.2.1.Experimental analysis

The results of the fully-reversed strain-controlled low-cycle fatigue experiments at different strain amplitudes for the four investigated alloys are summarized in Fig.4.Only two loading conditions were reported for the Mg85Zn6Y9alloy as above 0.75% strain the specimen broke in the first tensile ramp and below 0.5% strain,no macroscopic plastic deformation could be measured.

Fig.4(a–d)depicts the peak stress evolution of the four alloys.An increase in strain amplitude tends to slightly increase the peak tensile stress but not the peak compressive stress for the Mg99.2Zn0.2Y0.6alloy.Hence,a positive mean stress appears for this material.In addition,limited softening is observed at 0.5% strain amplitude,characterized by a decrease in both the tensile and compressive peak stresses.This softening is also noticed in the Mg97Zn1Y2alloy which can therefore be attributed to a softening of theα-Mg grains.On the other hand,no notable difference and change in peak stress with the applied cycle was observed for the two other alloys.A clear increase in the peak stress with the increase in the LPSO phase volume fraction was also noticed.

To clarify the deformation mechanisms,Fig.4(e–f)reports the stress-strain hysteresis curves at half-life for the four alloys.The Mg99.2Zn0.2Y0.6alloy exhibits a clear asymmetrical shape with a sigmoidal concave portion under tension loading which is characteristic of a detwinning activity.In particular,pseudo-elasticity is observed upon load reversion after peak compression as it shows a different slope than after unloading past the peak tensile stress.Hence,despite the significant grain refinement which often hinders deformation twinning,it is still an active mechanism likely located in coarse un-DRXed grains.Since the cyclic softening is mainly related to a decrease in the peak compressive stress,this suggests that deformation twinning becomes easier and easier with the cycle number.This is in good agreement with the in-situ ebsd analysis of Hazeli et al.on AZ31 Mg alloy[43].On the other hand,other alloys exhibit symmetrical hysteresis curves typical of a material mainly deforming by dislocation slip.We can note nonetheless a saturation of the compressive peak stress at strain amplitudes above 1.0%.which may suggest the onset of deformation twinning.The maximum applied strain may therefore be too low for the twins to have a clear effect on the hysteresis.

Fig.4.(a–d)Tensile and compressive peak stresses against the number of cycle and(e–h)stress–strain hysteresis curves at half-life for the strain-controlled experiments of of the four investigated Mg alloys.

Fig.5.Plastic strain amplitude against the number of cycle to failure for the four investigated alloys.

The plastic strain amplitudes against the number of cycles to failure are reported in Fig.5 for the four investigated alloys.The plastic strains were estimated from the hystereses at half-life by substracting the elastic strain to the total strain.Since,α-Mg and LPSO phase exhibit different stiffness(Table 1),a different Young’s modulus estimated from the first tensile ramp was used for each alloy.While Mg99.2Zn0.2Y0.6and Mg97Zn1Y2alloys show relatively similar fatigue lives,a clear decrease in fatigue life is observed for a given plastic strain amplitude in the case of Mg89Zn4Y7and Mg85Zn6Y9alloys.Since,low-cycle fatigue life is mainly controlled by the capacity of the material to accommodate plastic deformation,it highlights the decrease in ductility with the increase in the LPSO phase volume fraction.A recent study of Takagi et al.[44]revealed the high tensile ductility of single LPSO crystal.The main difference between single and polycrystals stems from the constraint effects to the presence of grain boundaries preventing an easy rotation of the crystal and eventually promoting stress concentration at the interfaces.

This is confirmed by the fracture surfaces of the different alloys depicted in the SEM micrographs in Fig.6.While we observe clear regions distinguishing the initiation,propagation and final failure stages in Mg99.2Zn0.2Y0.6and Mg97Zn1Y2alloys,these regions are absent in the two other alloys which exhibit flat fracture surfaces with the presence of cleavagelike facets typical of brittle failure.In addition,initiation sites revealed flat facets which were related to the LPSO-phase in the case of the three alloys containing LPSO grains.It is worth pointing out that multiple facets may be observed on the edge of the Mg89Zn4Y7alloy specimen(Fig.6(c)),which suggests multiple initiation sites.It was inferred that these facets originated from a high tensile stress acting on specific crystallographic planes due to the absence of deformation mechanisms accommodating out-of-basal plane strain[45].This assumption is discussed in the upcoming section in view of the numerical analysis.

3.2.2.Numerical analysis of stress–strain partitioning

To clarify the individual effect of each phase on the cyclic behavior of Mg/LPSO two-phase alloys,strain-controlled cyclic simulations were conducted on four synthetic microstructures representing the four investigated alloys,with similar conditions than in experiments.Fig.7(a–d)represents a phase map of the generated microstructures based on the procedure presented in previous section.A relatively high fidelity could be achieved by the proposed method.

Fig.7.(a–d)Phase map of synthetic microstructures and(e–h)comparison of the first cycle experimental and numerical stress-strain hysteresis curves of(a,e)Mg99.2Zn0.2Y0.6,(b,f)Mg97Zn1Y2,(c,g)Mg89Zn4Y7 and(d,h)Mg85Zn6Y9 alloy.

The crystal plasticity parameters were fitted separately for theα-Mg and the LPSO phase based on the first stress-strain hysteresis curves of the cyclic tests of Mg99.2Zn0.2Y0.6and Mg85Zn6Y9alloys,respectively.The obtained parameters were then validated by predicting the cyclic behavior of the two Mg/LPSO two-phase alloys.Fig.7 depicts the cyclic stress-strain curves in the first cycle for the four alloys,the crystal plasticity parameters are summarized in Table 2.As observed previously,limited cyclic hardening/softening was observed in the two single phase materials and in the two Mg/LPSO two-phase materials[20]which explains the fact that it was neglected in this study.The higher strength of basal dislocation in the LPSO-phase compared with theα-Mg phase may be related to the presence of a large number of kink boundary within the LPSO phase produced by the extrusion process.These boundaries decrease the mean free path of dislocation and may therefore contribute to a strength increase of the corresponding phase.A much lower detwinning strength compared with the twinning one was selected on the basis of previous work[27]as an attempt to reproduce the pseudo-elastic behavior generally observed in Mg alloys upon load reversion.This pseudo-elasticity was related to the fact that thin twins are relatively unstable and may easily undergo detwinning upon unloading.Even though the proposed model is phenomenological,it is able to catch this phenomenon as the sigmoidal portion of the hysteresis curve is well reproduced(Fig.7(e)).Comparing the predicted and experimental stress-strain hysteresis curves of the two Mg/LPSO two-phase alloys,Mg97Zn1Y2and Mg89Zn4Y7,a very good agreement is observed.A slight discrepancy may be noted in Fig.7(b)in the initial slope of the detwinning portion which is related to the fact that the crystal is not fully rotated prior to unloading due to the pseudo-slip approach used in this study.Hence,it does not accurately predict the change in the elastic stiffness.

Fig.8.Distribution of accumulated slip shear strain,accumulated twin shear strain and maximum crystallographic normal stress for(a)Mg99.2Zn0.2Y0.6,(b)Mg97Zn1Y2,(c)Mg89Zn4Y7 and(d)Mg85Zn6Y9 synthetic microstructures subjected to strain-controlled low-cycle fatigue conditions at 1% strain amplitude.

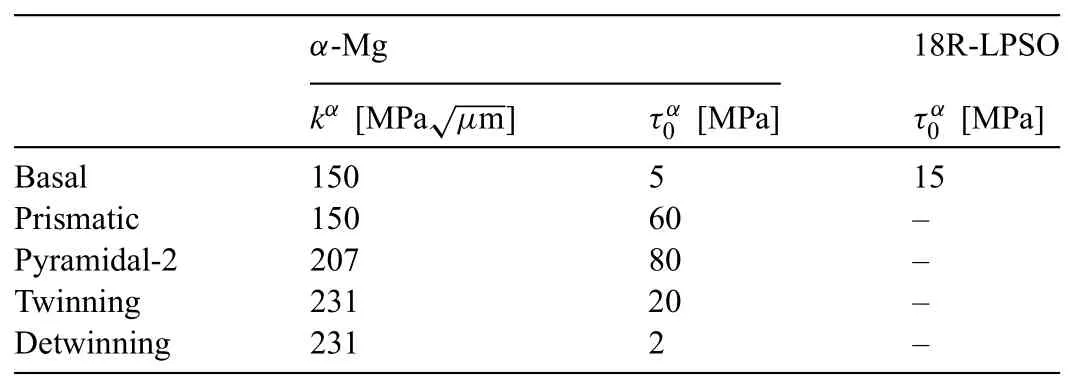
Table 2Estimated crystal plasticity parameters.

Analyzing the predicted stress-strain hysteresis curves,twinning activity was also predicted in the alloy containing about 25% LPSO-phase.This is in good agreement with experimental data as monotonic compression tests of Mg97Zn1Y2alloy revealed that deformation twinning still occurs in this material despite the significant grain size reduction[17].In particular,a larger twin fraction was observed in unDRXed regions[46].An increase in flow stress with the increase in the LPSO-phase volume fraction was noted.Hagihara et al.[9]attributed this strength increase to multiple combined mechanisms:grain refinement,crystallographic texture,short-fiber reinforcement by the LPSO-phase and solid solution strengthening.In particular,the effect of the LPSOphase was inferred based on a simple mixture rule for composite materials.To clarify these observations,the local mechanical fields should therefore be investigated.The first two rows in Fig.8 depicts the distribution of accumulated slip shear strain and accumulated twin shear strain for the four microstructures subjected to a 1% strain amplitude cyclic loading.The accumulated slip shear strain distributions include the contribution of all the available slip systems for a given phase.However,there was almost no pyramidal slip activity in theα-Mg grains so the distribution mainly represents the basal and prismatic slip activity.Increasing the volume fraction of LPSO phase also appears to increase the intensity of basal slip in LPSO grains.Overall,the plastic deformation is highly heterogeneous both inside grains and between grains.In particular,only a few LPSO grains in the 85% and 100% LPSO alloy exhibit significant plastic activity.The size effect introduced by the Hall-Petch type relationship naturally favors plastic activity in largest unDRXedα-Mg grains.These softer regions also promote plastic activity in their vicinity which tend to form relatively wide shear bands.On the other hand,the scattered presence of needle-like LPSO grains seems to limit the size of these shear bands to the LPSO phase interval and therefore to more evenly distribute the strain,especially in the 25% LPSO alloy.In this regard,the LPSO phase indeed works as a short-fiber reinforcement such as in composite structures[9]by preventing the formation of large plastic zone and therefore increasing the flow stress of the material.Hence,controlling the spatial distribution of the LPSO phase may contribute to a greater improvement of the strength of this composite structure.Deformation twinning is also predicted to take place in large grains favorably oriented.It is notably observed that unDRXed grains undergoing deformation twinning tend to deform by basal slip as well but the opposite is not necessarily the case due to the significant strength discrepancy between the two deformation modes and their different sensitivity against the grain size.Increasing the LPSO phase volume fraction tends to reduce the proportion of twinned grains which is mostly related to the decrease in the number and size of unDRXed grains.

The investigation of the fracture surface revealed the presence of large quasi-cleavage like facets in the LPSO phase at the initiation sites of both the 100% LPSO and the Mg/LPSO two phase alloys[20]under low-cycle fatigue conditions.The last row of Fig.8 shows the distribution of the maximum normal stress acting on all the slip planes at the peak tensile load during the strain controlled test at 1% strain amplitude.In the case of the LPSO phase,the normal stress acting on both the basal plane and the three prismatic planes were investigated even though only basal slip was considered.Logically,regions with low plastic activity exhibit high stress.A strong discrepancy in the stress intensity is noticed between the Mg grains and the LPSO grains which is due to the absence of deformation modes accommodating out-of-plane deformation and to the significant discrepancy in the C11elastic component(Table 1).Interestingly,the highest normal stresses are not only observed in the 100% LPSO grains but also in the 25% and 85%.These highly stressed regions are located at the interface betweenα-Mg and LPSO grains.The facets observed experimentally are therefore likely to be the results of these locally high tensile stress due to the strong strength discrepancy between the two phases.It is worth pointing out that mean field approaches are unable to evaluate local fields heterogeneity and the effect of the spatial distribution of the different phases and may therefore only be used to quantify the local average fields.

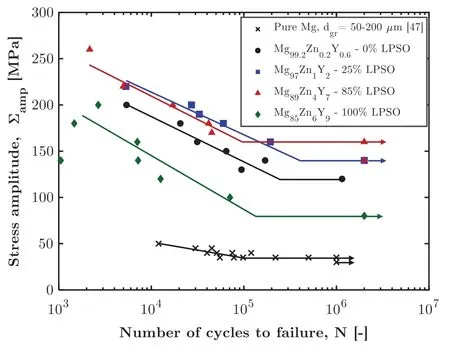
Fig.9.Stress amplitude against the number of cycles to failure for the four alloys under load-controlled high-cycle fatigue conditions.The experimental results of Xu et al.on pure Mg alloy are also reported[47].

3.3.High-cycle fatigue behavior

3.3.1.Experimental analysis

The results of the load-controlled high-cycle fatigue tests are reported on the S-N diagram in Fig.9.To assess the effect of the grain size distribution on the fatigue behavior,the experimental data of Xu et al.[47]on extruded pure Mg are also reported as their material exhibited similar crystallographic texture but an average grain size ranging from 50 to 200μm.The fatigue limit of their material was about 30–35 MPa.Due to the limited number of specimen used for each investigated alloy,the precise estimation of the fatigue limit was not possible in the present study.Nonetheless,comparing the behavior of pure Mg with that of Mg99.2Zn0.2Y0.6containing nearly 0% LPSO phase,we note a significant increase in both the fatigue life and the fatigue limit.Since,the main difference between these two materials is the grain size distribution,such improvement in fatigue performance can therefore be attributed to the grain refinement.Mg97Zn1Y2and Mg89Zn4Y7alloys exhibit relatively similar fatigue lives,but an increase in the fatigue limit can be observed with the increase in the LPSO phase volume fraction.Namely,the estimated fatigue limit was about 120 MPa,140 MPa and 160 MPa for the Mg alloys containing 0%,25% and 85% of LPSO phase,respectively.On the other hand,the fatigue behavior of Mg85Zn6Y9containing about 100% LPSO phase showed a major drop in the high-cycle fatigue behavior with a fatigue limit of about 80 MPa.A significant scattering of the fatigue life was also noted for a similar stress amplitude which may be attributed to the presence of initial defect in some specimens.Hence,we observe a non monotonic,convex relationship between the fatigue limit and the LPSO phase volume fraction.In particular,mixture rules cannot be applied for the fatigue behavior as it would predict a decrease in the fatigue limit with the increase in LPSO volume fraction.

Fig.10.SEM micrograph of(a-b)fracture surface and(c-d)crack initiation of(a,c)Mg99.2Zn0.2Y0.6 and(b,d)Mg85Zn6Y9 alloy under high-cycle fatigue conditions at of stress amplitude of 180 and 160 MPa respectively.

Fig.10 depicts the fracture surfaces of Mg99.2Zn0.2Y0.6and Mg85Zn6Y9specimen subjected to load-controlled highcycle fatigue.Initiation,propagation and final failure stages are observed in both specimens,but the propagation region appears much smaller in the latter one due to a much lower fracture toughness of the LPSO grains[48].Large facet is noted at the initiation site of Mg99.2Zn0.2Y0.6(Fig.10(c))which strongly suggests crack initiation from un-DRXed grains.On the other hand,initiation site is much smaller in Mg85Zn6Y9(Fig.10(d)).The fracture surfaces of Mg97Zn1Y2and Mg89Zn4Y7are very similar to that of Mg99.2Zn0.2Y0.6and Mg85Zn6Y9,respectively.It was notably found that crack initiation also originated fromα-Mg grains in both Mg97Zn1Y2and Mg89Zn4Y7[20].However,no large facets were observed in these cases.Hence,the fatigue limit is likely to be related with the initiation mechanism inα-Mg grains.

3.3.2.Investigation of a fatigue indicator parameter

To understand the increase in fatigue limit and fatigue life with the increase in LPSO phase volume fraction for the three Mg alloys:Mg99.2Zn0.2Y0.6,Mg97Zn1Y2and Mg89Zn4Y7,a series of simulation on synthetic microstructures were carried out under load-controlled fatigue conditions.Specifically,for each of the three alloys,ten unique microstructures with the same dimensions as in the low-cycle fatigue study were generated based on the developed procedure.They were loaded under fully-reversed conditions with varying stress amplitudes and a fatigue indicator parameter(FIP)meant to quantify the driving force for crack initiation was investigated.In a previous study[27],it was found that a slip-based critical plane FIP derived from the Tanaka-Mura model for crack initiation[49],could correctly predict the anisotropy in fatigue life of an extruded Mg alloys when loaded either along the extrusion or transverse direction.The FIP was given by:

whereΔγαis the shear strain range accumulated in one cycle on a slip band of length dαof the slip systemα.The FIP was estimated on multiple potential crack paths in eachα-Mg grain based on the trace of the different slip planes[38].According to the Tanaka-Mura model formulated in a strainbased form[50],the investigated FIP is inversely proportional to the number of cycle for crack initiation Nini∝1/FIPα.Hence,crack initiation was assumed to occur in the grain maximizing the FIP.

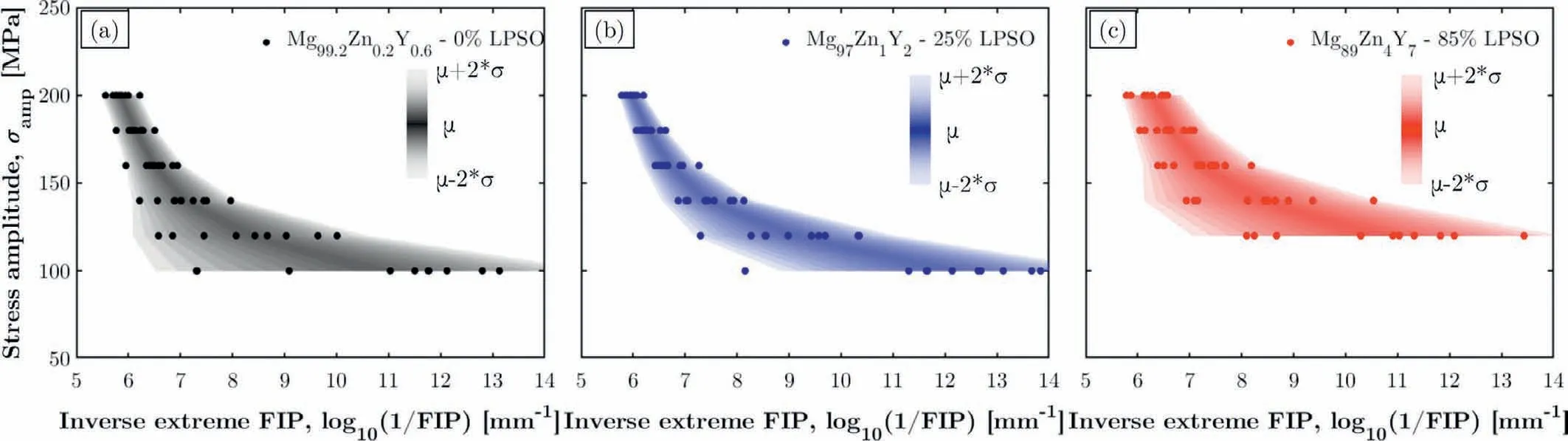
Fig.11.Distribution of the extreme inverse FIP per aggregate for(a)Mg99.2Zn0.2Y0.6,b Mg97Zn1Y2 and(c)Mg89Zn4Y7 alloy at different stress amplitudes.

Fig.12.Slip band length against the plastic shear strain amplitude of the extreme FIP per aggregate for(a)Mg99.2Zn0.2Y0.6,b Mg97Zn1Y2 and(c)Mg89Zn4Y7 alloy at different stress amplitudes.

Fig.11 represents the inverse extreme FIP for each of the ten simulated microstructures of the three investigated alloys,against the applied stress amplitude.Colormaps indicate the scattering of the data around the mean value.Due to the strength discrepancy between the different slip systems and the strong crystallographic,crack initiation is predicted to always take place on basal slip system.For high stress amplitudes,between 200 and 160 MPa,relatively similar crack initiation lives are observed for the three alloys with the average lowest one noted for the Mg99.2Zn0.2Y0.6alloy and the highest one for the Mg89Zn4Y7alloy.The scattering of the initiation life is relatively limited in this stress amplitude range which suggests that the plastic activity is homogeneous between generated microstructures.Once the stress amplitude decreases,a significant increase in the variability and change in the slope of the extreme inverse FIP is observed for the three alloys.It is also noticed that at 120 MPa,the Mg89Zn4Y7alloy presents almost the same scatter-band than the two other alloys at 100 MPa which suggests a higher fatigue limit for this material.

Since the FIP defined in Eq.(8)introduces a competition between the length dαof a slip band and its plastic activityΔγα,it is interesting to investigate the distribution and evolution of these parameters with respect to the stress amplitude to clarify the origin of the scatter changes in Fig.11.Fig.12 reports the slip band length against the plastic shear strain amplitude of the highest FIP in Fig.11 for the three alloys and the different applied stress amplitudes.The simulation of ten unique microstructure for each alloy naturally introduces a variability of the initiation sites both in terms of slip band length(vertical scattering)and plastic strain(horizontal scattering).As a general observation,the variability of these two parameters decreases with the increase in the stress amplitude for both alloys which suggests that initiation sites remain the same as the plastic deformation is more uniform.At low stress amplitude,typically at 120 and 100 MPa,a significant scatter of both quantities is observed,especially for Mg99.2Zn0.2Y0.6and Mg97Zn1Y2alloys highlighting a change in the initiation site for some microstructures.Hence,the high scattering at low stress amplitude in Fig.11 may be associated with a relatively heterogeneous distribution of the plastic activity.It also suggests that the relationship between the local plastic activity and the applied stress amplitude is different within each grain as we would have predicted the same initiation site independently of the loading condition otherwise.In addiction,while the plastic strain does not exhibit significant difference for the three alloys,the initiated slip band length tends to decrease with the increase in the LPSO phase volume fraction.As can be seen in both the EBSD map in Fig.2 and the phase maps in Fig.7,the size of the unDRXed grains tend to decrease with the LPSO phase volume fraction as the higher yttrium content promotes dynamic recrystallization.At low stress amplitude,crack initiation is indeed predicted to occur in unDRXed grains in 5 cases,2 cases and 1 case for Mg99.2Zn0.2Y0.6,Mg97Zn1Y2and Mg89Zn4Y7alloy,respectively.In other cases,crack initiation occurs in larger than average DRXed grains.The improved initiation lives and fatigue limit may therefore be associated with the decreasing presence of coarse unDRXed grains which appeared to be favorable site for crack initiation(Fig.10(c)).It should be pointed out the considering cyclic softening in unDRXed regions may contribute to a better fatigue behavior difference between Mg99.2Zn0.2Y0.6and Mg97Zn1Y2alloys but at the cost of a significantly increased computational cost as it would require the simulation of a possibly large number of cycles to reach the stabilized stage.

4.Conclusions

The fatigue behavior of four extruded Mg–Zn–Y alloys containing different LPSO phase volume fraction was investigated by a combined experimental-numerical comparative analysis.A numerical procedure based on a twoscale anisotropic tessellation was presented for the generation of multi-phase synthetic polycrystals reproducing key microstructural features of Mg/LPSO two-phase alloys that is a bi-modalα-Mg grain size distribution and needle-like LPSO grains.A phenomenological crystal plasticity model including dislocation slip and deformation twinning was calibrated against stress–strain hysteresis curves of single phase alloys containing either onlyα-Mg or LPSO grains.The model was then confronted to Mg/LPSO two-phase alloys and good agreement between experimental and predicted hystereses were found,thus supporting the proposed modeling approach.The flow stress increase with LPSO volume fraction was associated with a decrease in mechanical twinning activity due to a lower amount of unDRXed grains and the presence of elongated LPSO grains limiting the extension of wide shear band across the microstructure.Cleavage-like facets in LPSO grains under strain-controlled conditions were related to high tensile stresses acting on prismatic planes,especially at the Mg/LPSO interface,due to the absence of deformation mechanisms accommodating out-of-basal plane strain in LPSO phase.A significant decrease in the fatigue performances was noted for the alloy containing about 100% LPSO phase.This was associated to the lower fracture toughness of LPSO grains and a different initiation site compared with the three other alloys where crack initiated fromα-Mg grains.A slip-induced crack initiation criterion was finally investigated that predicted similar initiation lives at high stress amplitude and an increase in the fatigue limit with the increase in LPSO phase volume fraction.The scattering increase was associated with a higher plastic strain heterogeneity and a shift in initiation sites.The improvement of fatigue behavior with LPSO phase volume fraction was related to the decreasing presence of large unrecrystallizedα-Mg grains which were observed to be favorable crack initiation sites.

Data availability

The raw/processed data are available from the corresponding author upon reasonable request.

Acknowledgments

This work was partially supported by the JSPS KAKENHI for Scientific Research on Innovative Areas”MFS Materials Science”(Grant no.JP18H05478)and the JSPS KAKENHI for Early-Career Scientists(Grant no.20K14604).