并联混合动力汽车ECMS的时变等效因子提取算法的研究*

李跃娟，齐 巍，王 成，张 博，卢 强

（1. 北京工业大学机械工程与应用电子技术学院，北京 100124；2. 中国汽车技术研究中心有限公司，天津 300300）

前言

面对大气污染加剧和石油资源消耗过度的紧迫形势，汽车的环保与节能引起了广泛的社会关注，我国三部委联合颁布的《汽车产业中长期发展规划》的八大重点工程中的智能网联汽车推进工程和先进节能环保汽车技术提升工程为混合动力电动汽车节能研究带来了新的机遇［1］。由混合动力系统控制策略的对比分析可知，基于道路工况的实时优化控制策略对提升能源管理效率具有显著效果，是当前能量优化管理的研究热点之一［2-6］。全局优化是指根据固定的整个循环工况的特征，以全局油耗最小或效率最大为优化目标［7］。全局优化的算法有模拟退火［8］、遗传算法［9］、动态规划（dynamic programming，DP）［3］和拉格朗日乘子法等。采用全局优化算法控制策略，受到控制器计算能力的限制，难以用于实车［4］，而以等效燃油消耗最小策略（equivalent fuel consumption minimization strategy，ECMS）为代表的实时优化，因其结构简单、运算量小而被广泛应用［10］。为了获得更准确的油电转换系数，He 等［11］根据动力电池荷电状态SOC（state of charge）采用惩罚函数对电功率部分进行了加权处理；而Musardo等［12］则是根据驾驶工况结束后放电与充电的能耗对油电转换系数进行选取，进而可根据车辆运行的历史信息和预测信息对油电转换系数进行调节更新，从而保障电池SOC在一定范围内的平衡和最佳的燃油经济性惩罚函数，使得该策略具有良好的电量保持特性。大部分学者认为具有电量保持需求的混动车辆SOC 波动范围较窄，因此忽略了状态变量SOC对等效因子的影响，近似地认为等效因子为一个恒定的值，并未考虑基于工况的时变等效因子对ECMS 的影响。为保证ECMS 控制策略具有良好的电量保持特性，一些学者开展基于惩罚函数的自适应ECMS 算法研究，但等效因子初始值的选取仍然采用了穷举法［10，13］，且通过相关惩罚函数修正后的等效因子并不能反映实际工况下的最优值。

针对以上问题，本文中以并联混合动力系统为研究对象，结合动态规划算法DP与等效燃油消耗最小算法ECMS 的各自优点，构建能量算法理论模型（ECMSwDP）［14］，将等效因子作为全局最优算法的控制变量，通过对等效因子的离散全局优化，获得基于工况的最佳时变等效因子，有效解决了传统穷举法选取等效因子初始值的难点问题。

1 并联混合动力系统

本文中以并联混合动力客车为研究对象，其动力系统主要由动力电池、发动机、驱动电机、离合器、耦合器、变速器和主减速器等组成，如图1所示。发动机输出转矩通过离合器与耦合器接合，电机直接与耦合器接合，转矩耦合器的输出轴直接与六速变速器输入轴相连。发动机与电机的转矩通过离合器耦合，通过对离合器的控制，可实现6 种基本工作模式间的切换：纯电机驱动模式、纯发动机驱动模式、发动机与电机联合驱动模式、行车充电模式、混合驱动再生制动模式和纯电动再生制动模式。

整车及动力系统参数如表1所示。

图1 并联混合动力系统结构简图

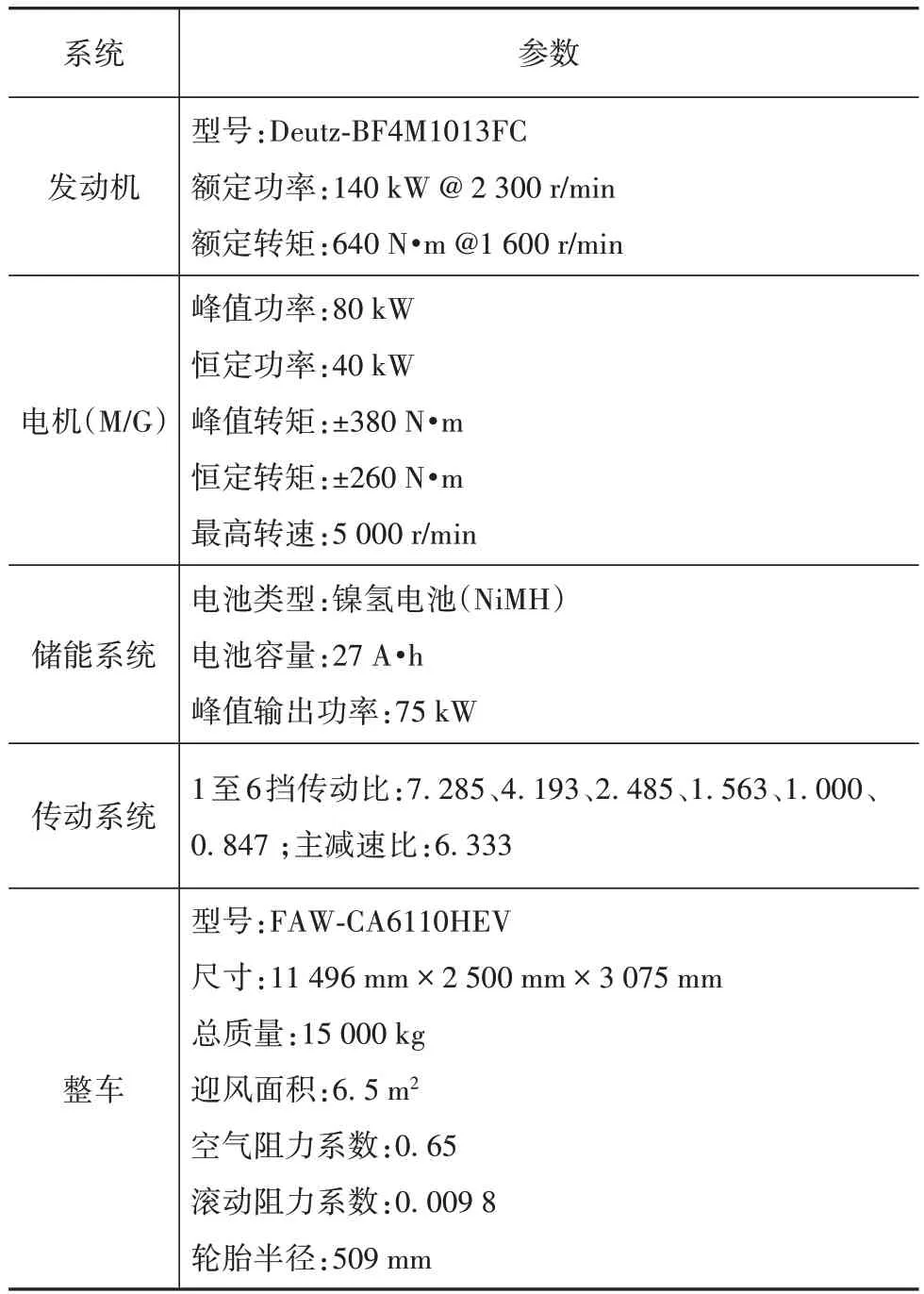
表1 并联混合动力客车整车及动力系统参数［14］

本文中算法研究均基于MATLAB/m 脚本环境中开发的前向准静态仿真模型，仿真模型中系统总成所涉及的准静态图（如发动机map、电机map 和传动系统效率图）均通过了Autonomie 仿真软件的验证，标准工况下燃油消耗率仿真结果与客车实际测试结果差值在5%以内［14］。

2 ECMS优化方法

ECMS 是基于庞特里亚金最小值原理（PMP）的混合动力汽车能量管理的一种实时优化方法，它被定义为通过等效因子将电机消耗的电能映射为等效的燃油消耗，旨在最小化瞬时等效燃油消耗以获取局部最优的控制量（转矩分配）［8］。ECMS 通过优化瞬时等效燃油消耗，获得优化控制量，等效因子通常由人为估计得到，而PMP 属于数值优化方法，通过最小化汉密尔顿函数求解最优控制量，数学上具有确定性的解。通过寻找ECMS 等效因子与PMP 协同状态之间的关系，来确定等效因子的调整规则，有利于获得ECMS 的优化解，因此，ECMS 可以看作是PMP的近似工程实现［15］。

PMP 应用于混合动力汽车能量管理策略，动力电池荷电状态SOC(t)设定为状态变量x(t)、发动机转矩Tice(t)设定为输入变量u(t)、燃油消耗率mf设定为目标代价函数L。由此，应用于混合动力汽车能量管理的PMP中的汉密尔顿函数H可以表示为

由汉密尔顿函数对应的物理含义，可以得出瞬时等效油耗ECMS表达式：

式中：mf，equ(t，u)为瞬时等效燃油消耗；mf(t，u)为发动机单位时间燃油消耗质量；Pele(t，u)为动力电池等效电能消耗；λ(t)为将电能转换为等效燃油消耗的等效因子；Hf为燃油低热值。

2.1 ECMS等效因子

ECMS 等效因子是将电机消耗的电能映射为等效的燃油消耗，反映了内燃机的化学能与电能相互转化的效率，旨在最小化瞬时等效燃油消耗以获取优化控制量。等效因子的选择决定了ECMS 算法的优化性能，是ECMS的关键控制参数。

PMP取得优化控制量的必要条件为

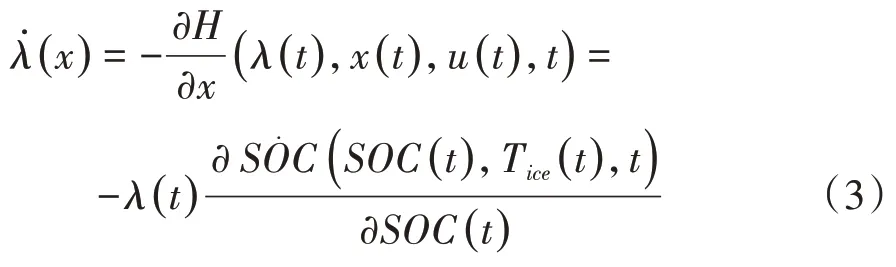
由式（3）可知，等效因子所反映的能量转化效率决定于状态变量SOC 的变化率（∀SOC）。根据是否考虑∀SOC，等效因子可划分为时变等效因子λ(t)和时不变等效因子λ，具体表达式如下：

由于车辆行驶工况未知，因此通常依据平均效率来估计筛选方法，获得车辆固定行驶工况下的最优时不变等效因子λ=λopt。

图2 为在北京工况下，不同的时不变等效因子ECMS 的SOC 轨迹图，以及基于全局最优DP 算法提取的SOC轨迹。通过轨迹对比可知，人工筛选（穷举法）的最优时不变等效因子λopt= 2.227 所对应的SOC 轨迹与DP 算法提取的轨迹非常接近；以λopt为参考值，微小地增加0.073（λ= 2.3）或降低0.127（λ= 2.1）时不变等效因子，SOC轨迹波动非常剧烈，说明动力电池充/放电对时不变等效因子λ敏感度较大。

图2 基于时不变等效因子ECMS 和基于全局最优DP 算法的SOC轨迹

2.2 ECMS算法的SOC惩罚函数

为解决这一问题，Jager 等［15］在 ECMS 算法中引入了SOC惩罚函数P(SOC)：

根据文章的表述可知，青少年自身具备的价值观与道德判断能力越强，出现攻击行为的频率将会大大降低。在此过程中，群体观作为一种集中体现社会取向的价值观，其个体价值发挥的越高，人际价值存在感将会越高。针对于此，笔者建议学校方面应该加强青少年价值观与道德判断方面的教学工作，教师应该起到正确的舆论引导作用，及时纠正个别学生行为上的偏差，有效约束与规范个体行为，确保青少年个体可以得到全面性发展、茁壮成长。

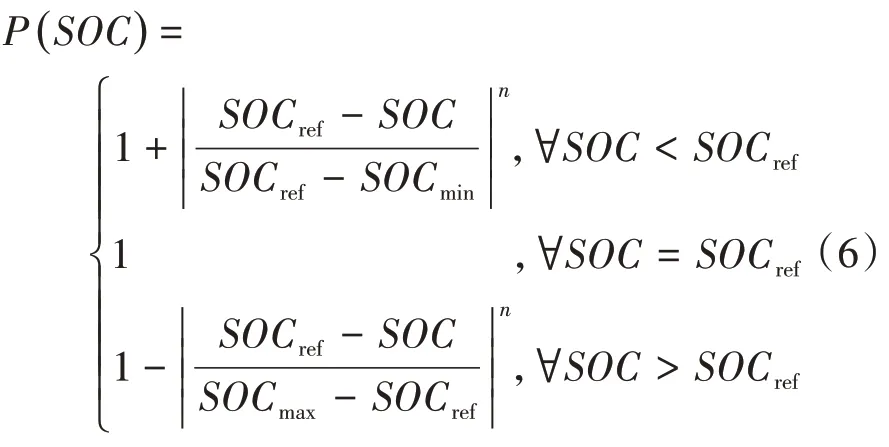
式中：SOCmin为 SOC 最小值，SOCmax为 SOC 最大值，SOCref为 SOC 参考值，三者分别设定为 0.4、0.6 和0.5；n为指数系数。

SOC 惩罚函数基本原理：根据电池SOC 反馈误差，惩罚函数每隔一定步长更新等效因子。更新方式为：等效因子随着电池SOC误差线性增加或减小，当电池SOC 值低于参考值时，等效因子增加，反之，亦然。引入惩罚函数后瞬时等效油耗ECMS表达式为

由图3可知，惩罚函数可以根据指数系数n来调节惩罚函数权重。当电池SOC 值偏离参考值时，惩罚函数P（SOC）≠1，通过调节指数系数，使电池SOC维持在参考值附近，确保并行混合动力客车的电量保持特性。

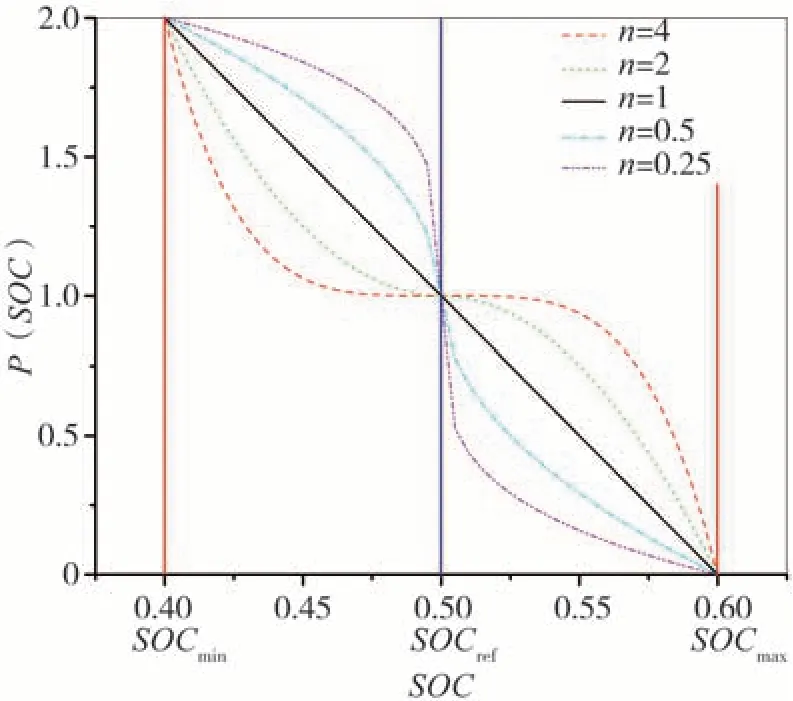
图3 指数系数n对惩罚函数的影响

为了比较惩罚函数对ECMS的影响，在图2的时不变等效因子ECMS 模型基础上添加了SOC 惩罚函数，在北京工况下，比较了带有SOC惩罚函数的时不变等效因子ECMS的SOC轨迹图，如图4所示。由图可见，在惩罚函数的作用下，初始值λ0= 2.3 和λ0=2.1 所对应的SOC 轨迹始终围绕在设定的SOCref=0.5附近波动。

虽然带有惩罚函数的ECMS 可以保证SOC 轨迹不产生如图2 所示的幅度较大的波动，但不同初始值λ0的选取仍然造成了SOC 的平衡问题，如图4 所示，当λ0= 2.3 时最终的SOCFinal仍然偏离初始SOCInitial较大，并不能确保并行混合动力车辆具有充/放电可持续性的要求。造成SOCFinal大幅度偏离SOCInitial的主要成因是人工估计的初始等效因子λ0与最优的等效因子λopt存在偏差。另外，实际控制策略中的工况是不断变化的，通过惩罚函数修正后的等效因子并不能反映实际工况下的最优时变等效因子。综上所述，开展基于工况的ECMS 时变等效因子研究是十分必要的。

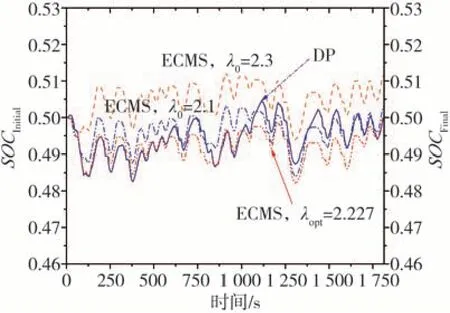
图4 带有SOC惩罚函数的ECMS对应的SOC轨迹

3 ECMS时变等效因子提取

ECMS 控制策略中的等效因子对于维持并联混合动力客车的SOC平衡以及实现最佳燃油经济性起到了至关重要的作用［10］。因此，根据汽车的行驶工况对等效因子进行动态管理，获得当前行驶工况下的最适合的时变等效因子λ(t)显得尤为重要。本文中结合动态规划算法与等效燃油消耗最小算法，构建新型能量算法理论模型即ECMS 与DP 相结合模型（ECMSwDP），以各时刻下并联混合动力客车燃油消耗率最小为优化目标，对驱动电机转矩和发动机转矩进行实时优化均衡控制。通过此新型算法可有效提取基于工况的ECMS时变等效因子。

3.1 ECMSwDP算法原理

ECMSwDP 算法是基于数值方法而非传统的解析方法。算法将等效因子作为控制变量，基于ECMS 目标代价函数mf，equ(t，u)最小，获得基于时间和等效因子的发动机与驱动电机的转矩与转速的数值库{Tice(k，λ)，Tem(k，λ)，ωice(k，λ)，ωem(k，λ)}；算法在计算过程中将基于数值库的值作为各变量值选取，从而实现了等效因子的最优状态变量选取，进而获得基于工况的时变燃油等效因子λ(t)。在满足一定约束条件下，ECMSwDP 算法求解目标函数值为ECMS 等效燃油消耗的最小值，如式（2）所示。在单纯DP 算法中，发动机转矩与转速变量(Tice，ωice)由参数变量(mf，Pele(t，u))替换，参数变量中的燃油消耗率mf与动力电池等效电能消耗Pele(t，u)分别由有效燃油消耗率（BSFC）图谱和动力电池能量方程计算获得。新型算法中的控制变量将由等效因子λ替换传统DP 算法中的发动机转矩Tice。ECMSwDP 算法中各时间步长k的变量需满足相应的不等式约束方程：

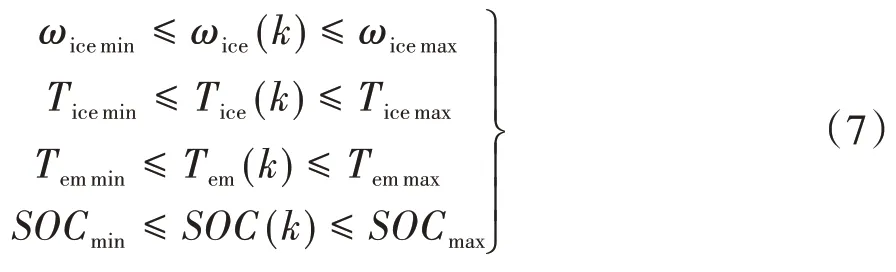
式中下标min 和max 分别表示系统变量的最小值和最大值。

3.2 提取时变等效因子计算过程

ECMSwDP 算法的控制/状态变量与对应的网格区间如表2 所示。其中控制变量的网格区间P介于设定好的最大与最小等效因子之间，其中控制变量的步长d(λ)大小设定为0.1；状态变量SOC 初始和最终值设置为0.5，SOC 的量化增量分别设置为0.000 1，时间步长k为1 s。

表2 ECMSwDP 算法的控制/状态变量与对应的网格区间

ECMSwDP 算法在每一时间步长k及每一控制变量网格点λ上计算获得最优的ECMS 目标代价函数mf，equ(t，u)以及最优代价函数所对应的发动机与驱动电机的转矩与转速和燃油消耗率。循环计算结束后，存储数据形成发动机与驱动电机的转矩与转速和燃油消耗率数值库：

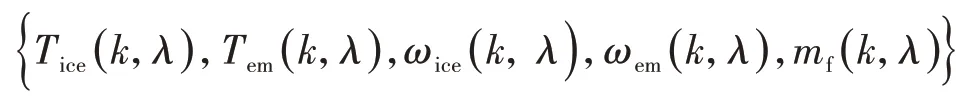
通过动力系统各参数数值库、等效燃油消耗率（BSFC）图谱以及瞬时SOC 计算公式，可获得每一时间步长的控制变量λ(k) ∈P所对应的燃油消耗率及状态变量数值库{mf(k，λ)，SOC(k，λ)}。

ECMSwDP 算法类似于单纯DP逆向最优搜索方式，以最终的状态变量为起点，寻找每个时间节点上的最优燃油消耗率网格点直到初始状态变量结束，同时存储最优选取点对应的状态变量、控制变量和动力系统各项参数，获取最优的ECMS 时变等效因子λ(t)。

4 仿真结果与数值验证

4.1 ECMSwDP算法仿真结果

基于MATLAB/m 脚本环境中开发的前向准静态仿真模型，以北京标准工况为例计算获得了时变等效因子λ(t)，如图5所示。

图5 ECMSwDP算法提取的时变等效因子

在工况的初始阶段（0～100 s），车辆处于加速状态，λ(t)值较低，从图中显示介于1.5～2.5，使用电能的代价较低，表明控制策略倾向于使用电能，SOC 轨迹也表明，电池电量下降速率较快。100～180 s工况阶段，车辆处于减速制动运行工况，λ(t)值较高，表明控制策略倾向于为电池充电，并且前100 s的电能消耗带来了SOC 的降低，腾挪出的蓄能空间可更大限度促使制动能量的回收，说明算法所提取的时不变等效因子是基于全局优化的结果。

算法所提取的时变等效因子的平均值λave=2.203，与图2 中人工筛选（穷举法）的最优等效因子值λopt= 2.227 非常接近，因此，可根据该算法提取的不同行驶工况的时变等效因子对应的均值来解决穷举法选取等效因子初始值λ0的难点问题。

4.2 时变等效因子验证分析

为验证ECMSwDP 算法所提取的时变等效因子λ(t)在实时的ECMS 控制策略的自适应能力和节油效果，在北京工况条件下，对时变等效因子ECMS 和单纯DP 控制策略各自运行参数，如动力电池SOC、发动机与电机瞬时功率Pe与Pm和累计燃油消耗的工况响应轨迹以及转矩与转速工作点作对比分析，如图6 和图7 所示。基于时变等效因子的ECMS 与全局最优算法DP的动力电池SOC响应轨迹、发动机与电动机的功率轨迹和转矩与转速工作点高度相似。因此，实现兼顾全局优化及实时优化的ECMSwDP 算法，能够改善以等效因子为核心的等效燃油消耗最小策略的控制效果，解决了如何通过算法选取最优等效因子的问题。

图6 时变等效因子ECMS运行参数的工况响应轨迹

4.3 平均时变等效因子验证分析

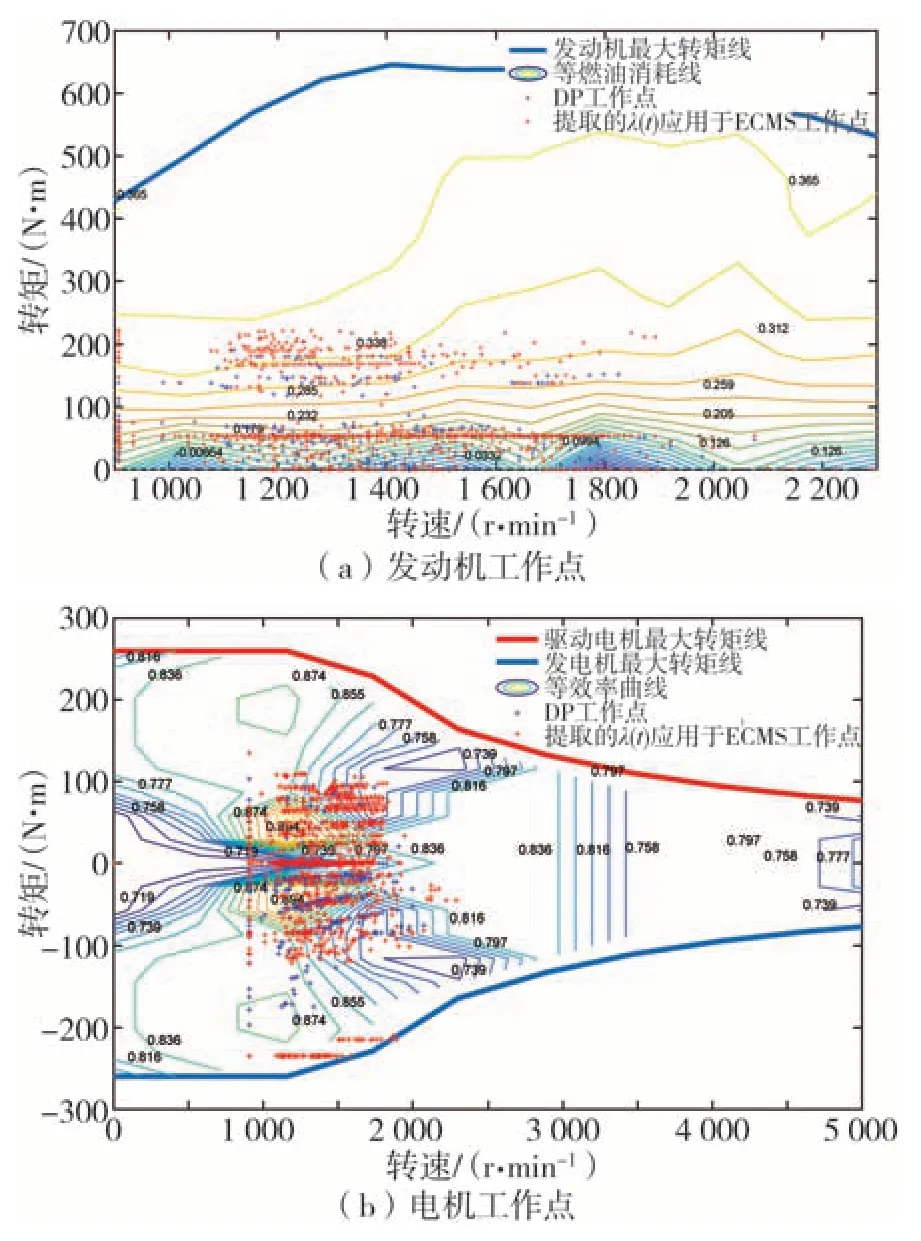
图7 时变等效因子ECMS运行参数的工况响应工作点

为验证4.1 节中所提取的时变等效因子平均值λave= 2.203 与人工筛选最优等效因子λopt= 2.227的值相接近的这一发现，将基于ECMSwDP 算法所提取的平均时变等效因子作为ECMS 和带有惩罚函数的ECMS+P（SOC）控制策略中的等效因子初始值，基于已验证的前向准静态仿真模型，在北京工况条件 下 进 行 验 证 分 析 ，ECMS、ECMS+P（SOC）和ECMSwDP 各自运行参数工况响应轨迹如图8 所示，对比分析了动力电池SOC、等效因子和发动机与电机瞬时功率Pe与Pm的轨迹。

图8 平均等效因子的ECMS和ECMS+P（SOC）的运行参数工况响应轨迹

由图中各 SOC 轨迹可知，单纯 ECMS 的 SOC 轨迹与ECMSwDP 的SOC 最优轨迹偏离较大，两者最终SOC差值（ΔSOC）为0.018 1；带有惩罚函数ECMS的 SOC 轨迹与最优 SOC 轨迹高度相似，ΔSOC仅为0.007 8。从等效因子轨迹图的局部放大区间可清晰地发现，ECMSwDP 算法时变等效因子轨迹（蓝色虚线）与带有SOC 惩罚函数ECMS（ECMS+P（SOC））的动态等效因子轨迹（红色实线）的波峰、波谷重合度不高。原因是：全局最优ECMSwDP 算法的时变等效因子是基于车辆运行工况下各参数的优化均衡控制实时优化的，ECMS+P（SOC）的动态等效因子并不是基于实际工况下的最优时变等效因子，而仅仅是基于SOC反馈误差的调节获得的。

4.4 各类算法验证结果分析对比

基于4.1和4.2节各类型算法仿真验证结果，获得在北京标准工况下的SOC差值（ΔSOC=SOCFinal-SOCInitial）、ΔSOC补偿后的燃油消耗量和各燃油消耗量的DP 差值，见表3。为了进一步验证算法的有效性，选取了接近公交车行驶工况特性的美国西弗吉尼亚大学城市工况（WVU city cycle）、郊区工况（WVU suburban cycle）和 0.7 倍的州际工况（WVU interstate cycle）的整合工况（WVU‑CSI）工况进行数值验证，见表4。基于北京工况、WVU‑CSI 工况的验证结果表明：ECMSwDP 算法的燃油消耗量与DP 差值和ΔSOC值最小，说明该算法是接近全局最优的解决方案。基于平均时变等效因子的ECMS+P（SOC）算法的燃油消耗量与ECMSwDP 相接近，虽然存在一定的ΔSOC差值，但平均时变等效因子仍然是一种基于最优化计算，解决人工选取等效因子初始值λ0这一难点问题的有效方法。

表3 基于北京工况的各类算法燃油消耗量及ΔSOC

表4 基于WVU⁃CSI工况的各类算法燃油消耗量及ΔSOC

5 结论

（1）以并联混合动力汽车为研究对象，构建能量算法数值模型（ECMSwDP），将等效因子作为全局最优算法的控制变量，通过对等效因子的离散全局优化，获得基于工况的最佳时变等效因子λ(t)，仿真结果表明，提取的λ(t)应用于实时的ECMS 能量控制策略中的燃油经济性与全局最优化算法DP 的差值仅为3.42%（北京工况）、5.96%（WVU‑CSI工况），证明了算法的有效性。

（2）平均时变等效因子能够有效解决穷举法选取等效因子初始值的难点问题，验证结果表明，平均时变等效因子作为等效因子初始值应用于ECMS+P（SOC）能量控制策略，其燃油消耗量与DP 差值为3.61%（北京工况）、10.51%（WVU‑CSI 工况），证明了该方法的可行性。

综上所述，结合动态规划算法DP与等效燃油消耗最小算法ECMS 的优点所提取的时变等效因子在能量管理策略的实时优化中具有一定的可行性和有效性，可为基于车联网环境下道路信息的自适应实时优化控制策略提供理论基础和方法参考。