基于电机最优回馈转矩曲线的制动控制策略*

曾小华，陈虹旭，宋大凤，崔 臣，李占江，蒋元广

（1. 吉林大学，汽车仿真与控制国家重点实验室，长春 130022；2. 南京越博动力系统股份有限公司，南京 210000）

前言

面对日益严峻的环境和能源问题，汽车产业正经历由传统汽车向新能源汽车的转变。其中，电动汽车与混合动力汽车发展迅速，并具有良好的市场前景。作为关键部件之一，驱动电机的运行特性大大影响电动车和混合动力车的行驶性能。永磁同步电机（permanent magnet synchronous motor， PMSM）具有功率密度大、运行效率高、控制器成本低等优点，广泛应用于新能源汽车领域［1］。

永磁同步电机可分为表贴式和内置式两种结构，由于内置式PMSM 永磁体安装于转子铁芯内部，电机机械强度高，容易实现弱磁升速［2］。在电机的输出转矩和功率不变的前提下，提高驱动电机的最高转速可以降低电机体积和质量，提高功率密度，因此内置式PMSM非常适合作为车用驱动电机。

对于混合动力车辆，提高燃油经济性的有效手段之一是利用驱动电机回收再生制动能量，制定合理的制动控制策略以回收更多的能量。Ko 等［3］针对并联式混合动力车辆，提出一种基于模糊控制的制动分配策略，实现再生制动与液压制动的协调控制；Kumar 等［4］针对后轮驱动的串联式混合动力车，在传统并联制动控制策略基础上提出一种新的并联协同控制策略，在实现制动回收能量提升的同时保证了驾驶员的制动感觉不变；靳立强等［5］为提高电动轮汽车的再生制动能量回收率，设计了一种模糊控制器，并以UDDS 循环进行了仿真；潘清贵［6］针对混联式HEV 轿车设计了4 种制动模式，并提出了基于行星排外齿圈回馈制动转矩优化的控制策略；郭金刚等［7］为实现电动汽车单次工况能量回收率最优，提出了一种基于制动强度控制的再生制动控制方法。

以上文献缺少对车用驱动电机制动特性的分析，忽略了电机在低转速下回收效率低甚至不能回收的问题。针对这一问题，卢东斌等［8］针对四轮轮毂电机驱动的电动汽车，分析了表贴式永磁同步电机的制动特性，并给出了能量回馈状态的切换条件。综合以上的研究现状，进一步分析车用内置式永磁同步电机的制动特性，结合电机制动特性对电动车和混合动力车的制动回收潜力进行探究具有理论和实际意义。

本文中针对车用内置式永磁同步电机，基于PMSM 等效电路模型建立了电机的数学模型，分析了PMSM 的回馈制动状态和耗能制动状态，以及两种制动状态的切换条件；结合电机矢量控制策略解析出控制电流指令id、iq随转矩和转速的变化曲面，计算得到最优回馈转矩曲线，并据此提出一种回馈能量最优的制动控制策略；针对某一正在研发的P4构型混合动力商用车，在不同的循环工况下，对比分析并联制动控制策略与本文所提出的回馈能量最优的串联制动控制策略下的制动回收能量和燃油经济性的提升效果。

1 内置式永磁同步电机制动原理

根据内置式永磁同步电机的等效电路模型，建立其数学模型，得到电机在驱动和制动状态下的相量图，分析了电机处于回馈制动状态和耗能制动状态下的条件。

1.1 永磁同步电机数学模型

内置式永磁同步电机在d⁃q轴上的等效电路模型如图 1 所示［9］。其中，ud、uq分别为d、q轴电压，id、iq分别为d、q轴电流，Rc为铜损电阻，Rf为铁损电阻。将PMSM 运行过程中产生的铜损和铁损视为流经Rc和Rf产生的热损耗，idt、iqt分别为d、q轴上的转矩电流，idf、iqf分别为d、q轴上的铁损电流，Ld、Lq分别为定子绕组的d、q轴电感，ψf为转子永磁体磁链，ωe为电机电角速度。

图1 内置式PMSM等效电路模型

根据图1，得到d、q轴电压表达式为

其中udf和uqf可表示为

铁损电流可表示为

内置式PMSM输出电磁转矩为

式中p为极对数。

PMSM的输入功率为

1.2 车用PMSM 制动特性分析

当电机稳态运行时，式（1）可表示为

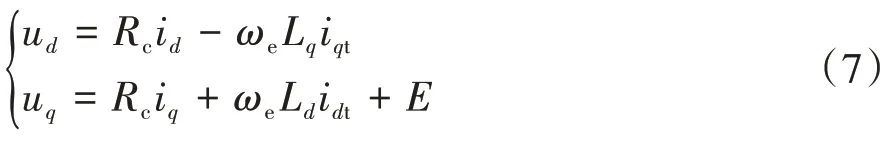
式中E为电机反电动势，E=ωeψf。

基于式（7），可绘制内置式PMSM 在驱动和不同制动运行状态下的相量图，如图2所示。

图2 内置式PMSM在驱动和制动状态相量图

图中U和Is分别为电机的电压和电流矢量，j 表示电压在相位上超前电流90°。

由图2（a）可见，PMSM 在驱动状态下，电压矢量U在相位上超前于反电动势E，U与电流矢量Is间的夹角φ小于90°，此时输入功率为正，即电机运行消耗能量。在制动状态下，通过控制q轴电流反向即可实现电机的制动控制，电压矢量U滞后于反电动势E，当反电动势E足够提供制动所需电流时，U与Is的夹角φ大于90°，如图2（b）所示，此时输入功率为负，电机向电池回馈能量，处于回馈制动状态。如果电机的转速较低，即反电动势E较小，不足以提供制动所需电流，如图 2（c）所示，U与Is的夹角φ小于90°，输入功率为正，电池向电机输出能量以保证制动需求，此时电机处于耗能制动状态。

可见，对于车用内置式PMSM，当电机处于耗能制动状态时消耗电池能量，只有处于回馈制动状态才能有效地回收制动能量，这与电机转速和控制电流有关。

2 制动回馈能量最优控制策略

由1.2 节的分析可知，当电机进行再生制动时，可通过控制电流指令id和iq使其处于回馈制动状态，同时，根据式（6）所示的电机输入功率表达式，当电机转速一定，合理控制电流指令可使该转速下输入功率最小，即向电池回馈的能量最大，以实现最优的制动回收能量。本节中针对某车用内置式PMSM，解析需求制动转矩与控制电流id、iq间的关系，得到id、iq随转矩和转速的变化曲面，采用Matlab软件计算电机进入回馈制动状态和回馈能量最优时的转矩—转速曲线，并据此制定了回馈能量最优的制动控制策略。

2.1 控制电流指令解析

在车用电机的运行过程中，整车控制器根据踏板行程等信号，向电机控制器发出转矩或负荷率指令，电机控制器通过控制电流实现对输出转矩的控制，为保证控制的实时性，控制电流指令id、iq一般通过电机转速和转矩查表得到［10］，再根据电机实际输出的转速和转子位置信号进行反馈修正。目前，车用内置式PMSM 常采用的控制策略为最大转矩电流比控制（maximum torque per ampere，MTPA）和弱磁控制。在基速之前，永磁同步电机为实现铜损最小，控制电流id、iq沿MTPA曲线移动。忽略铁损电阻（即式（4）中铁损电阻Rf趋于无穷大），内置式PMSM 的电磁转矩表达式如式（8）所示，MTPA 运动轨迹上id、iq满足式（9）所示关系［11］。

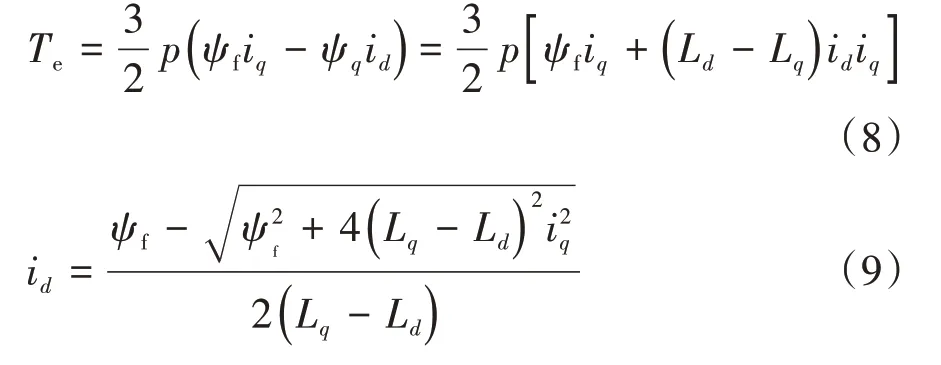
随着PMSM 转速升高，电机的反电动势增大，当反电动势大于逆变器能输出的最高电压时，控制电流将无法跟踪指令，因此对于车用高速驱动电机，在基速之后常采用弱磁控制以进一步升高转速，通过调整直轴电流id来削弱永磁体磁场。在电机实际运行中，电机的工作点通常落在如式（8）所示的恒转矩曲线与电压极限圆的交点上［12］，由于在电机高速运行时，定子电阻上压降很小，故忽略了定子电阻，稳态条件下电压极限圆表达式为

其中极限电压ulim与直流电源电压Udc满足如下关系：

联立式（8）与式（9）可得MTPA 控制下控制电流指令id、iq与转矩和转速的关系，联立式（8）与式（10），则可得弱磁控制下id、iq与转矩和转速的关系，将解析出的指令电流代入PMSM 输入功率表达式（6），即可确定当前工作点下的PMSM 输入功率，作为求解最优回馈转矩曲线的依据。

仿真所用车用电机主要参数如表1 所示。电机的d、q轴电感会受负载水平和激励大小的变化而变化［13］，Ld随d轴电流id的变化曲线和Lq随q轴电流iq的变化曲线，如图3所示。

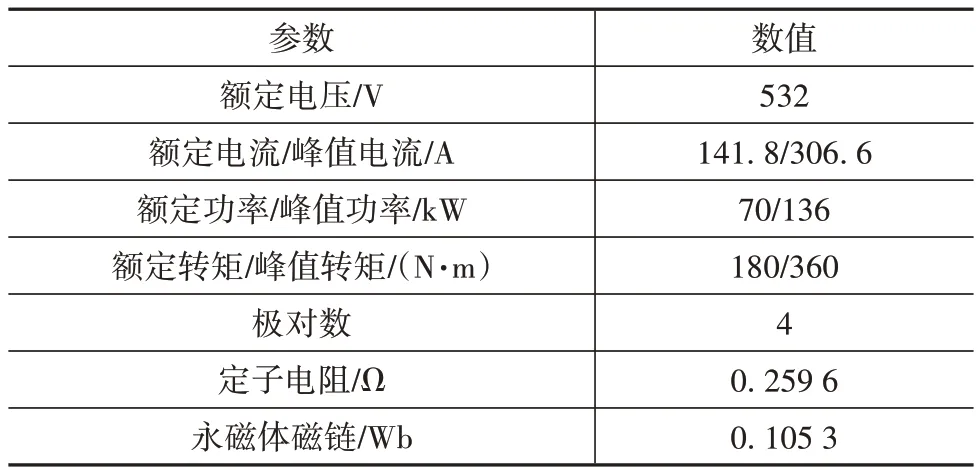
表1 电机主要参数

图3 电感参数随电流的变化曲线

将上述电机参数代入式（8）～式（11），得到控制电流指令id、iq随电机转速和转矩变化的MAP 云图，如图4所示。

2.2 电流指令解析验证

为验证控制电流解析指令的准确性，将由图4所示MAP 云图查表所得的电流指令与电机的台架试验数据进行对比。图5 为电机运行在500 与3 500 r/min 时，不同制动转矩下试验测得的交流电流与根据MAP 图查表计算得到的仿真值对比曲线。

由图5 可以看出，仿真得到的交流电流与实测数据的误差很小，在5 A 以内，因此可用图4 所示的MAP 云图来解析指令电流id、iq，为进一步求解最优回馈转矩曲线提供基础。

图4 控制电流指令随转速和转矩变化MAP图

图5 交流电流试验与仿真数据对比

2.3 基于最优回馈转矩曲线的制动控制策略

将电机的转速和转矩在运行范围内离散化，根据2.1 节的控制电流指令解析结果得到每一离散点处的电流id、iq，将其代入式（6）中，即可得到电机在每一运行工作点处的输入功率。当电机的转速一定时，求得输入功率最小时的制动需求转矩，该转矩即为该转速下的最优回馈制动转矩；在电机转速较低时，输入功率Pin＞0，此时电机处于耗能制动状态，计算出该转速下输入功率为负时的切换转矩，即可得到电机允许能量回馈转矩-转速曲线。

应用Matlab软件求得最优回馈转矩与允许能量回馈制动转矩曲线，如图6所示。

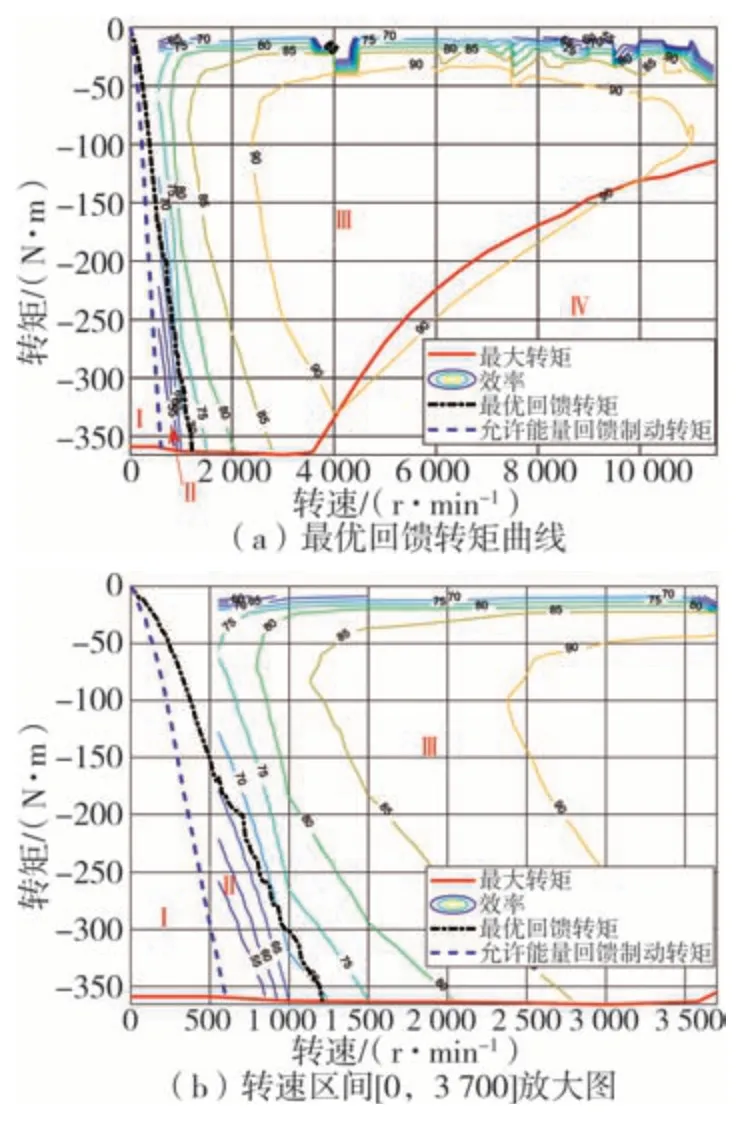
图6 最优回馈转矩曲线

图中Ⅰ区即为电机的耗能制动状态区，当电机工作点处于该区域内时制动将消耗能量。II区和III区为电机的回馈制动状态区，在该两区内制动可回收制动能量，其中，当电机工作点处于II 区时，电机提供最优回馈转矩曲线上的制动转矩，可实现输入功率最小，即回收功率最大，剩余制动转矩由机械制动补足。据此，制定基于最优回馈转矩曲线的制动回馈能量最优控制策略为：在车辆进行再生制动时，当需求制动转矩落在图6 所示的Ⅰ区与Ⅱ区时，控制电机输出最优制动回馈转矩曲线上的转矩；当需求制动转矩落在Ⅲ区时，电机输出所需要的制动转矩；当需求制动转矩落在Ⅳ区时，受到电机外特性的限制，电机输出最大转矩。

基于上述计算方法制定的基于最优回馈转矩曲线的制动回馈能量最优控制策略，在电动车和混合动力车进行再生制动时可以得到理论上最优的制动回收能量。

3 仿真分析

下面结合某P4 并联构型混合动力商用车，介绍了电动车与混合动力车辆常用的并联制动和串联制动控制策略，并分别在C‑WTVC、CHTC‑TT 循环工况和试验采集到的某段省道工况下，对并联制动和所提出的制动回馈能量最优的串联制动控制策略进行了仿真分析。

3.1 电动车和混合动力车的制动控制策略

电动车和混合动力车的制动控制策略应合理分配机械制动与电力制动的比例，同时考虑到结构复杂性和布置方案的可行性，目前常用的制动控制策略包括并联制动和串联制动两种控制策略。针对某P4 并联构型混合动力商用车，驱动桥为由发动机驱动的中桥和由电机驱动的后桥，车辆进行再生制动时只能回收电驱动桥上的制动能量，在电驱动桥上不同制动控制策略下的制动力分配示意图如图7所示［5，9］。

图7 不同制动控制策略下的制动力分配

由图7可见，并联制动控制策略1是指在电机制动力到达额定制动力之前，电力制动与总需求制动力呈一固定比例，到达额定制动力后，电机制动力保持不变，机械制动力继续增加；并联制动控制策略2是指制动踏板行程到达临界位置之前全部采用电力制动，临界位置之后电机制动保持额定制动力不变，机械制动随制动踏板行程的增大而增加；串联制动策略采用第2 节提出的基于最优回馈转矩曲线的回馈能量最优的制动控制策略。

在3 种控制策略中，并联制动控制比较容易实现，并联制动方案1 只需在原有制动系统中增加电力制动，并联制动方案2 需要修改原有的制动踏板自由行程；串联制动方案要求机械制动力能够实时调节，实现起来较为复杂。由于并联制动方案2 能比方案1 回收更多的制动能量，下一节将对并联制动方案2 和所提出的基于最优回馈转矩曲线的串联最优制动控制策略进行仿真分析。

3.2 仿真分析

对某P4 并联构型混合动力商用车进行不同制动控制策略下的仿真分析，整车基本参数如表2 所示，车辆构型如图8所示。

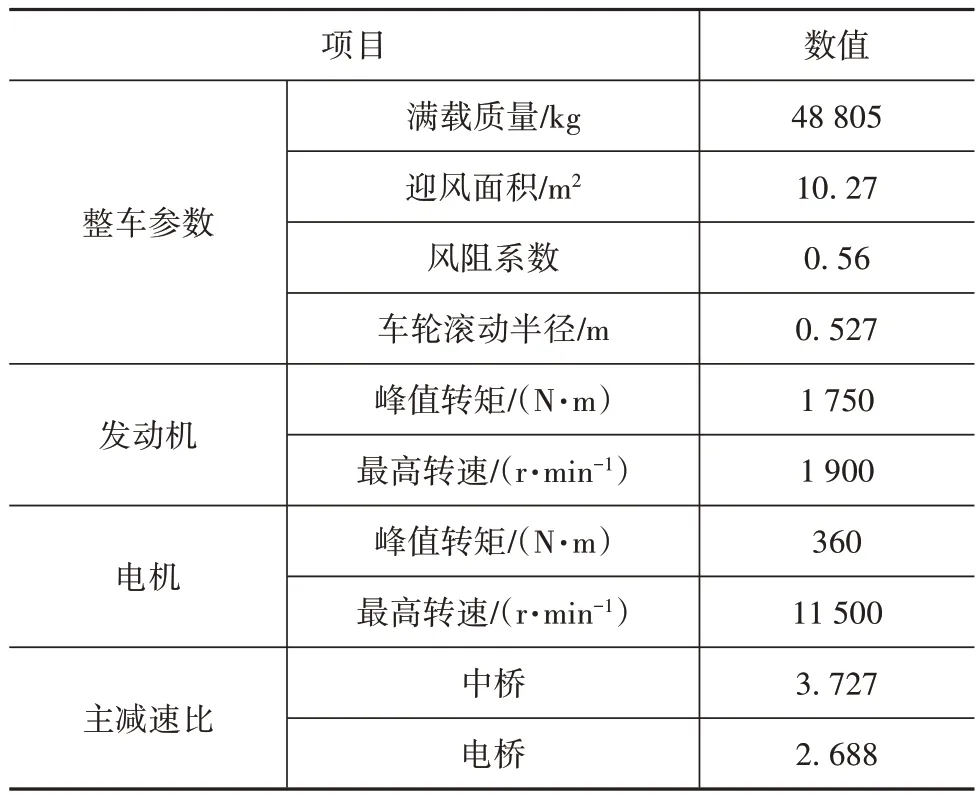
表2 整车基本参数

图8 驱动桥构型图

首先在C‑WTVC 循环工况下进行仿真，工况信息如图9所示。

图9 C‑WTVC循环工况信息

仿真所用能量管理策略为发动机最优控制策略，在并联制动和基于最优回馈转矩曲线的串联最优制动控制下的电机工作点分布分别如图10（a）和图10（b）所示。

由图10（b）可以看出，在电机转速较低时，电机的制动转矩控制在最优回馈转矩曲线上，满足回馈能量最优的串联制动控制策略的控制要求。两种制动控制策略下仿真结果如表3所示。

由表3 可见，该P4 构型混合动力车在C‑WTVC循环工况下理论驱动能量为170 433.37 kJ；仿真得到并联制动控制下再生制动回收能量为13 796.06 kJ，串联最优控制下再生制动回收能量为17 847.76 kJ。与并联制动控制相比，串联最优制动控制的再生制动回收能量提升了29.37%；再生制动能量与理论驱动能量之比提升2.38 个百分点，百公里油耗降低2.24%。验证了所提出的基于最优回馈转矩曲线的制动控制策略的有效性。

为进一步验证所提出的串联最优制动控制策略的有效性，分别以中国工况CHTC_TT 和某段省道工况进行仿真，工况信息分别如图11和图12所示。

图10 电机工作点分布

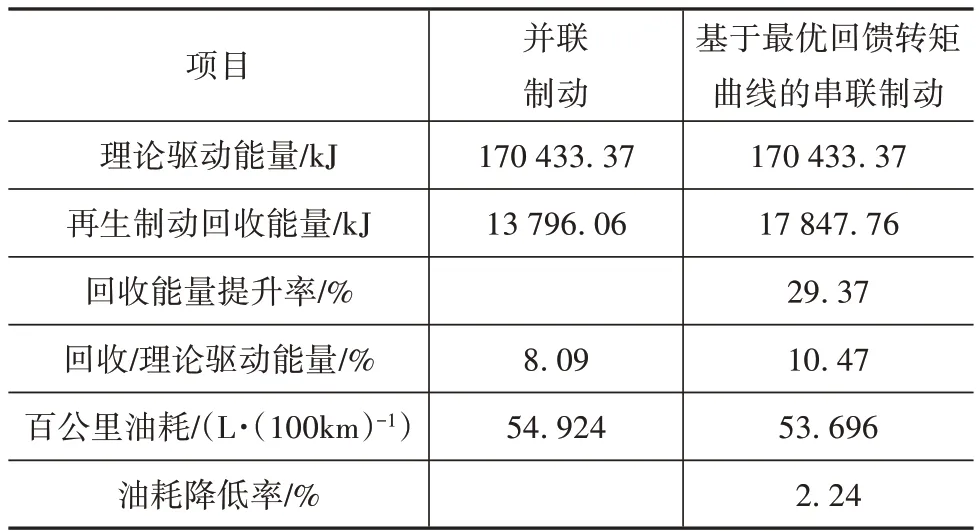
表3 不同制动控制策略下的仿真结果对比

图11 CHTC_TT工况信息

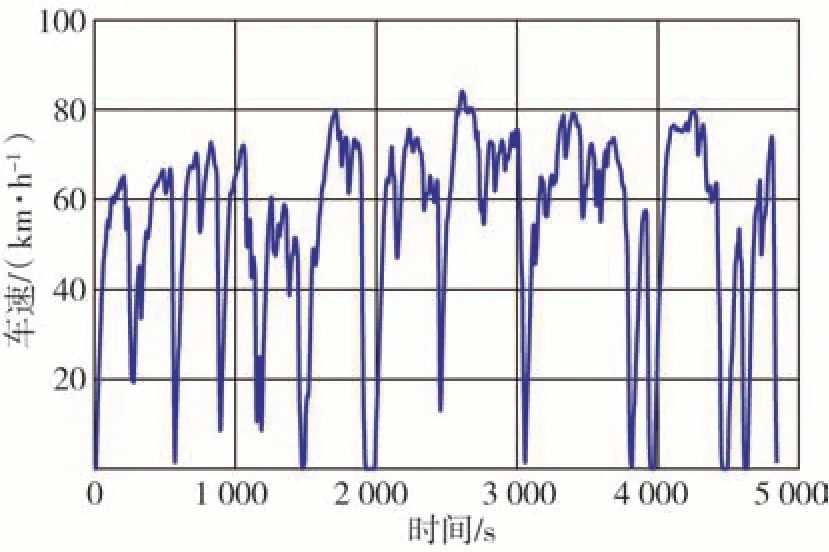
图12 某段省道工况信息

采用电机最优回馈转矩曲线的串联最优制动控制策略时，在CHTC_TT 工况和省道工况下的电机制动时的工作点分布情况如图13所示。由图13可见，两种工况下，当车速较低制动时，电机工作点均控制在了最优回馈制动转矩曲线上，得以尽可能多地回收制动能量。

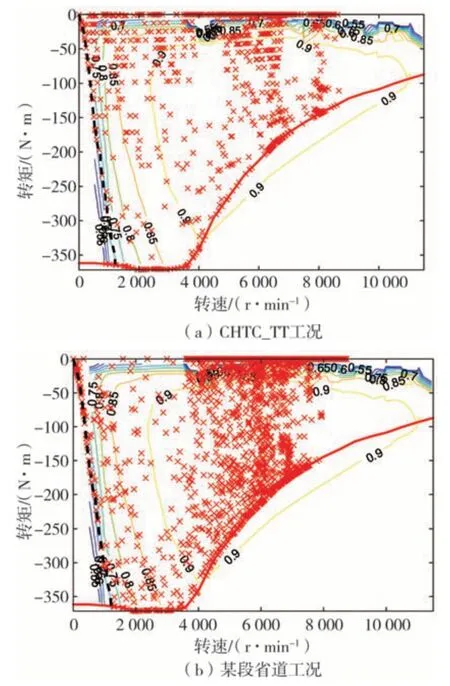
图13 两种工况下制动时电机工作点分布

在两种工况下比较并联制动与所提出的基于最优回馈转矩曲线的串联制动控制策略，百公里油耗与再生制动回收能量仿真结果如表4所示。

表4 不同行驶工况下仿真结果对比

由表4 可见，在CHTC_TT 循环工况下，与并联制动控制相比，采用所提出的串联最优制动控制策略的再生制动回收能量提升了14.48%，油耗降低了2.0%；在某省道工况下，再生制动回收能量提升率为21.09%，油耗降低率为2.7%。综合表3 的仿真结果可以看出，在不同的仿真工况下，所提出基于最优回馈转矩曲线的串联最优制动控制策略均可明显提升制动能量的回收率，从而降低油耗，提升车辆经济性。

4 结论

（1）根据电机的等效电路模型和矢量控制方法，对车用内置式永磁同步电机的回馈制动状态和耗能制动状态进行分析，提出一种电机最优回馈转矩曲线的求解方法，并基于最优回馈转矩曲线制定了串联最优制动控制策略，以实现理论最优的制动能量回收。

（2）分析了电动车和混合动力车常用的制动控制策略，对比并联制动和串联制动控制策略在能量回收效果和结构布置难度方面的差异；以不同循环工况对某P4 并联混合动力商用车进行仿真，结果表明，采用所提出的基于最优回馈转矩曲线的串联最优制动控制的再生制动回收能量和经济性比并联制动控制策略明显提升。所提出的最优回馈转矩曲线的求解方法可为车辆再生制动系统控制策略的开发、制动模式切换门限值的确定等提供参考。

（3）所研究的P4 构型混合动力车辆仅通过后轴进行电力制动，因此所提出基于最优制动回馈转矩曲线的串联制动控制策略未考虑车辆制动时不同轴之间的制动力分配问题，新能源车辆制动时行驶稳定性与经济性间的综合考虑有待进一步深入研究。