基于碰撞安全性的铝合金吸能盒轻量优化*

陈 静，徐 森，刘 震，唐傲天，吕 伟

（1. 吉林大学，汽车仿真与控制国家重点实验室，长春 130022；2. 一汽解放汽车有限公司商用车开发研究院，长春 130011）

前言

为尽可能减少车身结构的损坏和出于乘客安全性的考虑，国内外研究人员对防撞梁构件吸能盒进行了大量研究。Saenz‑Dominguez 等［1］对于 glass/UV cured vinylester 复合材料组成的半六角构件以及由此构件组成的吸能盒总成进行准静态和动态冲击试验，针对不同冲击速度，在厚度和几何相似、碰撞力相同的情况下，比吸能（SEA）变化明显。此外，研究发现，在同样冲击速度与厚度下，单个构件与总成的SEA 值相近，从吸能量预测和测试成本考虑，可用单个构件代替总成进行设计研究。Lee 等［2］在确定吸能盒安装空间、材料和最大允许变形量后，在概念设计使用包括离散正交设计和拓扑优化的方法确定详细设计阶段初步方案的截面形状，并针对拓扑优化的结果以及初定方案再次运用离散正交设计，获得最优吸能盒截面结构参数。结果表明，此结构具有良好的轻量化效果和吸能特性。重庆长安汽车的黄利等［3］分析了三点静压试验中，铝合金吸能盒焊接热影响区外侧拉应力超过其抗拉极限导致断裂的现象，并对“日”字截面吸能盒进行切除加强筋处理，通过仿真与试验证明上述方案在改善外侧拉应力的可行性。万鑫铭等［4］在确定吸能盒截面形状后，通过近似响应面优化方法对铝合金吸能盒结构参数进行设计，试验结果表明，优化后的设计方案，不但提升了吸能量，质量还减轻了58%。

本文中以一款匹配碳纤维复合材料保险杠防撞梁的铝合金吸能盒为优化设计对象，通过正交试验设计不同的吸能盒方案，并进行有限元建模及前处理，基于评价标准（比吸能、碰撞力等）确定结构基本形状参数，并通过基于Kriging 代理模型的多目标粒子群优化方法完成样本点抽样、近似模型构建以及多目标优化等工作，经台车试验和仿真数据对比，验证了优化方案的可行性。

1 基于正交试验的吸能盒结构优化设计

本文中采用正交试验方法，初步确定了吸能盒的形状。正交试验设计的设计变量为吸能盒锥角、溃缩孔分布和孔直径大小。对于溃缩孔分布，将吸能盒长度分为3 个区域，各区域溃缩孔直径可取不同水平，吸能盒结构设计因素水平如表1所示。

关于表1 中各个水平，A 因素的1 水平表示吸能盒锥角设成如图1（a）的形式；B因素的1水平代表吸能盒上溃缩孔分布如图2（a）所示，3个区域各分布2个溃缩孔；而C、D、E 分别代表3 个区域溃缩孔直径尺寸，1水平为4 mm，2水平为6 mm，3水平为8 mm。

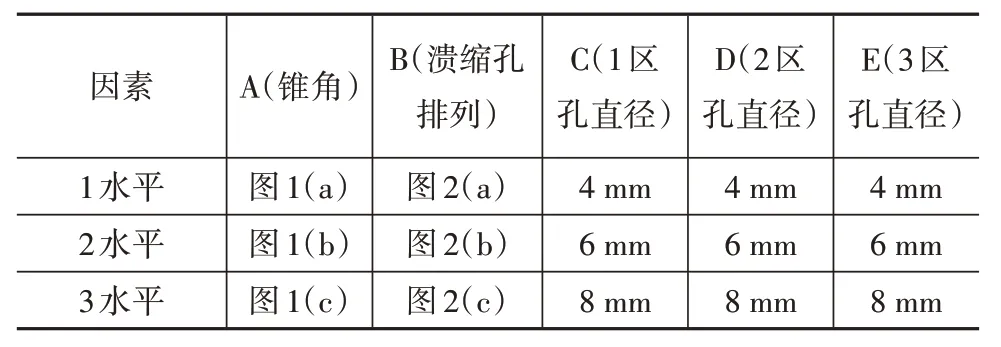
表1 吸能盒结构设计因素—水平表

图1 不同锥角吸能盒形状

图2 溃缩孔不同排列方案

考虑碰撞安全性和轻量化需求，试验设计中以吸能盒质量、碰撞力峰值、平均碰撞力、平均碰撞力与碰撞力峰值之比（CFE）、吸能盒的比吸能（SEA）和吸能盒与防撞梁粘接面积为评价指标。其中，碰撞力峰值Fmax表征吸能盒溃缩的难易程度，其值越小对碰撞性能越有利。平均碰撞力Faver和比吸能表征吸能能力，其值越大越好，粘接面积越小越好。针对以上因素、水平和评价指标，采用如表2 所示的L18（35）正交试验设计，相关仿真数据见表3。

对于正交试验数据，根据不同的评价指标进行极差分析，结果如下。

（1）峰值力指标最优组合为A1B2C1D1E1；主次因素为：A＞D＞C＞E＞B。

（2）平均碰撞力最优组合为A1B1C3D2E2；主次因素为：A＞B＞D＞C＞E。

（3）CFE（Faver/Fmax）指标最优组合为A1B2C1D3E 2；主次因素为：A＞C＞B＞D＞E。

（4）吸能盒质量指标最优组合为A3B3C2D2E3；主次因素为：A＞B=E＞C＞D。

（5）吸能量指标最优组合为A2B2C1D1E1；主次因素为：A＞D＞B＞E＞C。

（6）SEA（比吸能）指标最优组合为A2B2C1D1E 1；主次因素为：A＞D＞B＞E＞C。

（7）粘接面积最优水平为A1（因粘接面积只与吸能盒形状有关）。

对于吸能盒总是希望CFE值与比吸能SEA尽可能大，保证吸能盒足够的吸能特性。结合其他评价指标评测结果，确定吸能盒最佳性能组合为A1B2C1D1E1。确定各因素水平后对吸能盒进行几何建模，并进行相应前处理，吸能盒采用网格尺寸为10 mm 的壳单元划分，单元总数为1 184，节点数共1 256 个，同时与碳纤维复合材料防撞梁连接，最终建立的有限元模型如图3所示。

表2 吸能盒正交试验设计表

表3 吸能盒正交试验优化分析结果

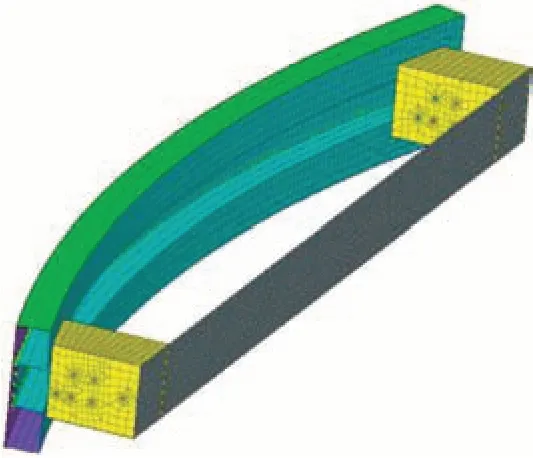
图3 前端结构有限元分析模型

2 吸能盒厚度的多目标优化

2.1 拉丁超立方法抽取样本点

采用拉丁超立方采样方法，将抽样厚度区间设置为［0.5mm，5mm］，抽取样本数设定为30，抽取样本点均匀分布在如图4所示的设计空间。

图4 吸能盒厚度拉丁超立方采样分布

通过对厚度因素进行采样，将获得的30 组拉丁超立方试验设计样本分别进行碰撞仿真求解，并得到30 组不同厚度因素的仿真数据（包括吸能量、峰值碰撞力和平均碰撞力等）。

2.2 基于Kriging 代理模型加点策略的多目标优化算法

2.2.1 Kriging代理模型

常用的近似模型主要有Kriging 模型、RSM 响应面模型和径向基神经网络模型RBF［5］等。本文中采用一种基于Kriging 代理模型加点策略的多目标粒子群优化算法对厚度变量进行多目标优化。

Kriging 模型［6-8］与多项式响应面模型和人工神经网络模型最大的不同之处在于，它不仅可以预测未知点的响应信息，还可以提供预测偏差信息。

对于任意给定的一组样本集X=[x1，x2，x3，…，xn]， 对 应 的 响 应 为Y=[y1，y2，y3，…，yn]T，上标为样本序号，而每个样本都是m维向量。Kriging模型假设系统的响应值与自变量之间的真实关系可以表示为

式中：μ为高斯过程的均值，属于确定性成分；z（x）为随机成分。z(x)～N(0，σ2)，且z（x）具有如下统计特征：

R项为样本点xi和样本点xj的相关函数，计算过程如下：

θk为相关向量，利用n个样本点线性加权叠加差值，基于预测值与真实值误差函数满足无偏估计，运用拉格朗日乘数法求解未知权系数向量，得到对于任意未知点x处预测值和预测标准差s2(x)为

式中：I为一个元素为 1 的n×1 的列向量；R为n×n的相关系数矩阵；r为待预测样本点与各样本点的n×1的相关系数向量。对于以上公式均涉及相关系数，问题最终转化为对θk的求解。由最大似然估计法求出θk时使式（5）最小：

以厚度因素为设计变量，基于响应值构建对应的Kriging 近似模型，经过检验，各指标R2值均大于0.9，其中CFE的验证曲线如图5所示。

上述结果证明构建近似模型是可靠的，可用于进一步优化。

2.2.2 粒子群算法与Kriging模型预测信息的结合

多目标粒子群算法所追求的最终目标是用尽可能少的计算资源得到覆盖整个搜索空间、靠近真实Pareto 前沿的非劣质解集。

当天下午，我就来到了周书记的办公室，周书记墙上那幅“静水流深”的字不见了，换成了毛泽东同志的题字“为人民服务”，虽然，毛泽东同志的题字是印刷出来的，却也装裱得很精致，挂在周书记头顶的上方，倒也显得很像那么回事的。

本算法在对种群初始化位置信息后，利用Kriging 模型提供的预测信息构建适应度y=f(x) +λimax(0，g(x))、相 应 的 目 标 函 数f(x) =[f1(x)，f2(x)，⋅⋅⋅，fl(x)]、对 应 约 束 函 数g(x) =[g1(x)，g2(x)，⋅⋅⋅，gw(x)]和偏差信息：

图5 CFE拟合优度检验

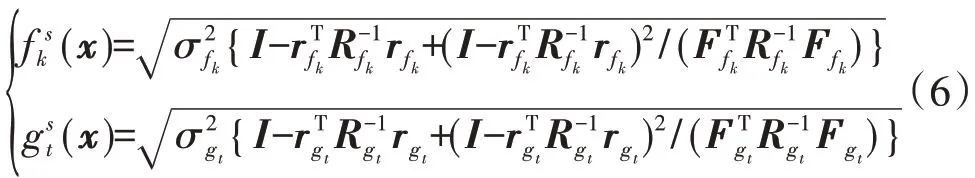
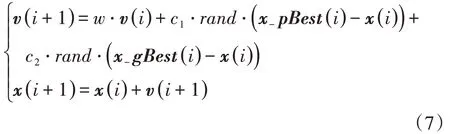
式中：w为粒子惯性权重系数；c1为粒子跟踪自身历史最优值的权重系数，且c1∈ [0，1]；c2为粒子跟踪群体最优值的权重系数，且c2∈ [0，1]；x-pBest(i)为第i个粒子的个体最优位置；x-gBest(i)为第i个粒子的全局最优位置。

计算更新后粒子的目标函数、约束、适应度函数和偏差信息，此过程执行包含对速度、位置偏离设计空间的调整。由于粒子位置发生改变，应在个体最优位置更新后再进行支配关系比较。从此次支配占优的个体与初始化占优非支配个体的相互支配关系中得到存入非支配解储备解集的非支配解，之后实施对非支配解储备解集的维护，以储备解集维护后的前20%非劣质解，更新每个粒子的全局最优位置信息。以预测偏差为导向，获取处于非支配解中前20%最小预测偏差粒子，得到更为精确的非劣质解集。对粒子执行变异操作：为保证在算法求解初期，有较大的探索性，应提供较大的变异率，在算法求解后期，变异率尽可能低一些，以保证算法的发掘性。

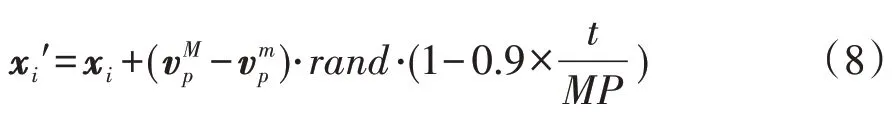
式中：MP为迭代总次数；t为当前迭代次数为变异后位置信息分别为第i个粒子关于第p个变量的速度上下限。

2.2.3 加点策略

算法通过多次迭代，最终获得对应Pareto 前沿。采用基于欧拉距离EIM 准则［9］的加点策略，构造相应的EI函数：

图6 算法主要流程

2.3 优化结果分析与高速碰撞仿真

在厚度优化问题中，以吸能盒比吸能SEA、平均碰撞力Faver作为目标函数，将最大碰撞力Fmax和防撞梁吸能量与吸能盒吸能量之比作为约束，即优化模型为

式中：Eb为防撞梁吸能量；Ec为与之匹配的吸能盒吸能量。考虑在低速碰撞时吸能盒不必产生较大溃缩，此时防撞横梁承担主要吸能作用，设置如式（10）所示的防撞横梁与新吸能盒吸能量比值阈值。为让算法在求解域内广泛搜索，设种群规模为40，最大迭代步数为50，最终得到的Pareto 前沿如图7 所示，图中f1为比吸能，f2为平均碰撞力。

图7 吸能盒厚度多目标优化的Pareto前沿解集

优化后吸能盒最优厚度为2.476 mm，考虑轻量化需求，厚度取2.4 mm，此时吸能盒比吸能为61.479 kJ/kg，质量为0.428 kg，平均碰撞力与峰值碰撞力之比CFE值为0.504，平均碰撞力为13.178 kN，峰值碰撞力为26.142 kN。

为验证吸能盒优化效果，与优化前吸能盒低速仿真工况结果进行对比，结果如表4 所示。由表可见：优化后吸能盒比吸能有较大提升，同时因峰值碰撞力下降而平均碰撞力略有增长，导致CFE增大，这说明优化后吸能盒吸能特性提升；从质量方面看，优化后吸能盒质量下降明显，在碰撞性能提升的同时实现了轻量化目标。

为验证设计方案在高速碰撞下仍具有可行性，将优化后铝合金吸能盒匹配碳纤维防撞横梁进行时速50 km/h 的刚性壁障100%重叠率正面碰撞仿真。同时，依据IHS内部试验标准，建立25%重叠度偏置柱撞试验模型，柱状物为固定不变形刚体，位于左前吸能盒之前通过吸能盒中心，柱状物直径为254 mm，设置碰撞速度为64 km/h，在定义接触和仿真时长后进行25%重叠度偏置柱撞仿真。图8 为刚性壁障100%重叠率正面高速碰撞下吸能盒变形和吸能的仿真结果。图9 为25%重叠度偏置柱撞吸能盒结构整体变形的仿真结果。

表4 优化前后吸能盒性能对比

图8 100%重叠率正撞吸能盒变形图

从图8 可见，吸能盒在7.5 ms发生轻微变形，并在之后变形加剧，在12.5 ms 时刻吸能盒已产生较大变形，吸收传递的碰撞能量随吸能量增大，吸能盒在15 ms 完全溃缩。由图9 可见，25%重叠度偏置高速柱撞中，随着加载时长推移，一侧吸能盒逐渐被压溃，另一侧仍能保持较好的结构稳定性。在这两个过程中，从吸能量角度，最大吸能量比低速碰撞都有明显提升。同时，在压溃过程中，吸能盒结构只发生X方向的溃缩吸能，并未发生吸能盒某一表面撕裂现象，且防撞横梁也没有发生断裂现象。说明高速碰撞下吸能盒具备足够的吸能特性，仍可发挥安全防护作用。

图9 25%重叠度偏置柱撞吸能盒变形图

3 低速台车碰撞试验对比验证

首先进行优化后结构的低速台车碰撞试验，汽车前端结构在低速冲击试验前须对防撞梁和吸能盒进行匹配连接。在本文中，碳纤维防撞梁低速仿真工况采用国标GB 17354—1998《汽车前后端保护装置》，完成该工况的仿真分析并与试验结果进行对比，如图10所示。因为防撞梁和吸能盒材料不同，考虑碳纤维材质特殊性，故优先采用胶粘方式完成防撞梁和吸能盒之间的连接。同时在防撞梁与吸能盒粘接边缘处采用铆接加强连接。图11和图12试验台车按照设定质量进行配重，并在吸能盒上标记测点位置以测量吸能盒侵入量。

图10 防撞梁与吸能盒的连接

图11 试验台车

图12 试验测点位置

根据仿真和台车试验采集的吸能盒测点位移变化量，进行相关数据对比分析，结果如表5所示。

表5 吸能盒仿真与试验测点位移对比

因低速碰撞下防撞梁变形量过小，各因素引起的很小变化都会产生较大百分比误差，因而采用绝对误差来衡量仿真与试验的误差程度。由表5 可见，吸能盒最大侵入量的仿真与试验值的误差仅为0.32 mm，且仿真与试验结果均表现出低速碰撞下吸能盒变形较小的趋势，说明低速碰撞仿真与试验较吻合，也说明了吸能盒优化设计可靠准确。

4 结论

通过正交试验的方法确定吸能盒结构的最优方案，并运用基于Kriging 代理模型加点策略的多目标粒子群算法实现了对吸能盒厚度的多目标优化。优化后吸能盒仿真与台车低速碰撞下测试位移的结果吻合良好，验证了吸能盒设计的可行性。对吸能盒优化前后结果进行对比分析可知，优化后吸能盒与防撞梁匹配连接良好的情况下，比优化前质量减少了23.84%，最大碰撞力下降了14.39%，CFE 值增长了18.31%，比吸能提升了47.54%，满足碰撞安全性和轻量化的设计要求。刚性壁障100%重叠率正面碰撞和25%重叠度偏置高速柱撞仿真结果显示，吸能盒结构具备良好的吸能特性，碰撞变形模式合理。