环形电流产生磁场的数理方程求解及COMSOL 仿真*

朱起源，陈学文

(重庆科技学院数理与大数据学院，重庆 401331)

1 引言

环形电流在空间产生的磁场是电磁学及电动力学讨论的典型模型之一，掌握环形电流产生磁场的研究方法和空间特征，有助于提升对物质磁性的理解，同时也是与磁场相关学科的应用基础。大学物理教材中一般只讨论了近轴及远场的磁场分布规律[1]。基于此，本文从理论和仿真两个角度出发，分别讨论环形电流产生磁场在全空间内的分布规律。

2 环形电流轴线上任一点磁感应强度

如图1 所示，本文所讨论问题可描述为：空间有一半径为R0的圆形导线置于图示坐标系xOy平面内，圆心位于坐标原点。导线中通有稳恒电流I，求在空间一点P产生的磁感应强度B。

图1 问题模型及坐标系示意图

原则上依据毕奥-萨伐尔定律，采用微元法将电流元产生的磁感应强度沿环形导线积分一周可得载流导线在空间某点产生的磁感应强度，即：

在计算轴线上磁感应强度分布规律时，由于积分具有高度对称性，因此可以很容易求得轴线上磁感应强度大小为

其中z为轴线上某点的坐标。磁场沿轴线方向，其指向与电流方向之间符合右手螺旋定则。

虽然也可以依据上述方法直接积分求得除轴线以外任意场点处磁感应强度的解析表达式[2]。也可以通过其它方式，例如借助高斯求积公式对此积分进行数值求解，但计算过程都相对复杂。下面我们用一种逻辑清晰，计算过程相对简单的方法对问题进行求解。

3 任意场点处的磁感应强度

我们先求解磁矢势A满足的定解问题，然后利用磁矢势与磁感应强度之间的关系B=∇×A求得磁感应强度。

首先由麦克斯韦方程组得稳恒电流产生磁场的矢势A满足微分方程

在介质分界面上矢势A满足的边值条件为

其中α为介质分界面上传导电流的线密度[3]。

如图1所示以圆形导线圆心为原点建立球坐标系。由对称性可知，矢势A只有φ分量，且只与r,θ有关，即A=A(r,θ)eφ[4]。因此由微分方程（1）得，矢势A的φ分量应满足方程

用半径为R0的球面将空间分为两部分，在内外两部分空间内均无传导电流，因此两个区域内矢势A的φ分量分别满足Laplace方程，即

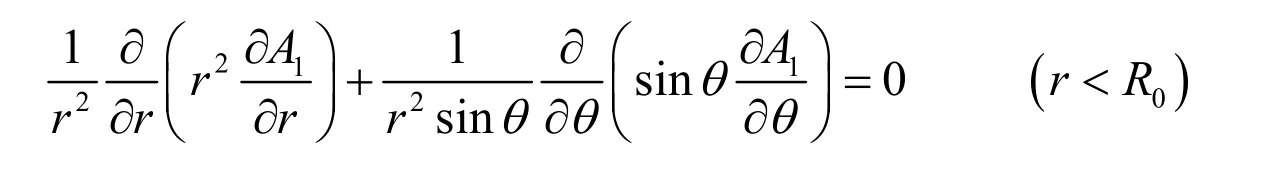
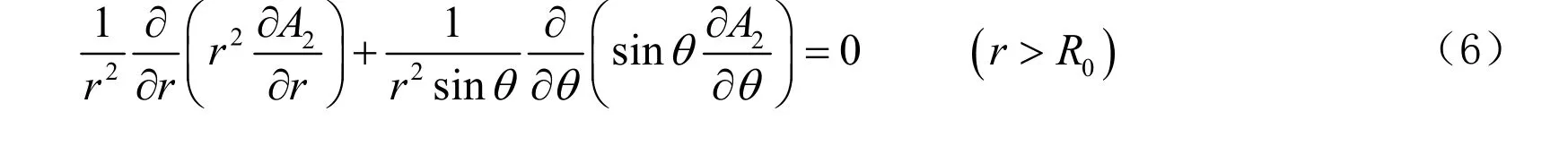
考虑到A在球心r=0 位置处应为有限值，即存在正数M，使得。在无穷远处，圆形导线可近似视为磁偶极子，根据磁偶极子在空间产生的矢势。并且在θ=0 以及θ=π时A均为有界函数。结合上述边界条件，由分离变量法可得通解

为了确定一系列未定系数al和bl，还需利用在球面上满足的衔接边值条件，将通解代入公式（2）得，在内外空间分界球面上有

在球坐标系下对矢势求旋度可得磁感应强度[5]，即

结合矢势A的对称性，有

4 磁感应强度的仿真计算

接下来使用基于有限元法的多物理场耦合仿真软件COMSOL Multiphysics对该问题进行仿真计算。为了方便设R0=0.35 m，I=1 A。为了尽可能还原理论计算结果，圆环的横截面积不应取得太大，在仿真过程中设定为半径为5 mm 的圆。使用AC/DC模块中磁场接口在半径为1.5 m 的球形空间内进行仿真研究。由于在空间产生的磁场具有轴对称性，因此在图2中只给出了yOz平面内磁感应强度分布的仿真结果。可以看出磁感应强度的分布满足右手螺旋法则，磁感线的分布规律也具有高度对称性。

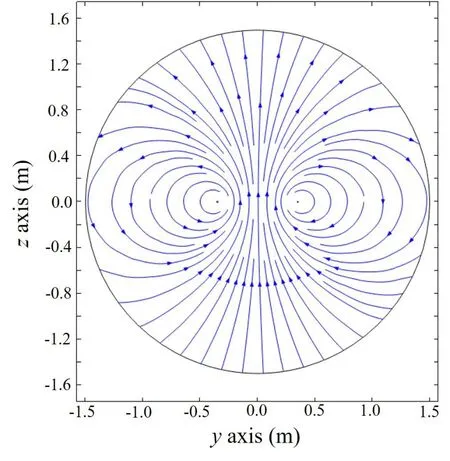
图2 yOz平面内磁感应强度分布的数值仿真结果

基于解析表达式（6）和（7），取上述级数解中前25项特定点处磁感应强度进行数值计算，然后通过坐标变换将计算结果转换在空间直角坐标系中。为了验证仿真计算结果的正确性，分别取z轴上解析解和仿真结果进行对比研究。如图3所示，在轴线上基于Comsol的仿真结果和理论计算得到的Bz的值几乎完全重合，可以看出数值仿真结果可以很好地反映磁场的分布规律。

图3 在轴线z 上磁感应强度 Bz 的Comsol仿真和理论计算结果对比

4 结论

本文首先利用分离变量法对环形导线产生的磁场进行了解析求解，相比于直接积分计算过程思路更直接，表达式也更加简洁。然后利用多物理场耦合仿真软件COMSOL Muliphysics 进行了仿真计算验证，仿真结果与解析解基本一致，也能够更加真实详细地还原物理模型。作为一个有效的数值仿真工具，在具体的应用实例中，如果定解问题中电流密度分布过于复杂，例如椭圆形环状电流[6]，则解析求解就变得非常困难，或者根本就不存在解析解，此时可以直接借助于COMSOL 等软件进行数值仿真求解。