基于停留时间分布的缠绕管内二次流研究
2021-03-06黄正梁王超郭燕妮杨遥孙婧元王靖岱阳永荣
黄正梁,王超,郭燕妮,杨遥,孙婧元,王靖岱,阳永荣
(1浙江大学化学工程与生物工程学院,浙江杭州310027;2浙江大学化学工程联合国家重点实验室,浙江杭州310027;3浙江省化工高效制造技术重点实验室,浙江杭州310027)
引 言
缠绕管换热器广泛应用于石油化工、空气分离、食品加工等领域[1−6]。与普通列管式换热器相比,缠绕管换热器特殊的紧凑结构提供了更大的传热面积[7−10],缠绕管内流体在离心力的作用下形成的二次流增加了管内流体的混乱程度,使传热速率显著提高,管内污垢热阻更小[11−14]。因此,掌握缠绕管内二次流的形成机制及其对管内结垢的影响规律,不仅是缠绕管换热器的设计基础,也一直是该领域的研究热点[15−16]。
缠绕管内二次流的研究方法包括墨水染色直接观察[17]、压降建模间接表征[18]和流体力学模拟计算[19]等。染色法在早期使用较多,可直接观察透明缠绕管中的二次流。研究者采用染色法发现了缠绕管中层流与湍流的转变行为与直管不同,缠绕直径和管径对缠绕管中流动具有显著影响[20−22]。染色法只能用于定性分析,不能提供定量的数据。压降可以反映缠绕管中的流动状态[23−24],有学者考察了缠绕直径、螺距、缠绕角度等结构参数对缠绕管压降的影响规律,建立了缠绕管压降的经验预测模型,通过与直管压降预测模型的对比,间接表征二次流的影响[24−28]。压降建模间接表征法不能揭示二次流的形成原因及其对压降的影响机制。近年来,一些研究者通过CFD 模拟研究缠绕管内的流动状态、二次流及其对传热的影响,证实了缠绕管和直管内的流动规律不同[29−35]。然而,由于缺乏缠绕管中二次流的检测方法和数据,不能对二次流的模拟结果直接进行验证[31,36]。
弯管中流体的流速分布不均、分子扩散和湍流扩散等因素,使得流体经过弯管时存在液体停留时间分布[37]。液体停留时间分布可以反映弯管中流体偏离理想流动的程度。有学者针对微流控设备,在缠绕管入口阶跃式注入示踪剂,测量出口液体停留时间分布,研究结果表明,相比其他流动形式,二次流可以减少缠绕管中的流体动力扩散[38]。也有学者通过脉冲式注入示踪剂的方法测量螺旋盘管和直管的液体停留时间分布,证明了螺旋盘管可以得到更好的停留时间分布[39]。受此启发,本文提出采用电导率法测量缠绕管内流体停留时间分布,利用无量纲方差表征二次流强度的方法。采用该方法研究了缠绕直径、缠绕角度、缠绕管管径等结构参数对缠绕管内二次流的影响规律。
1 实验装置及方法
如图1所示,实验装置由水槽、离心泵、流量计、缠绕管、电导率仪以及计算机等构成。如图2所示,实验中采用了7个长度均为4.6 m 的不锈钢缠绕管。缠绕管的结构参数见表1,实验介质为水,经离心泵增压后从水箱进入缠绕管内,其流量由转子流量计和阀门控制,在缠绕管出口检测电导率随时间的变化。缠 绕 管 中 的 流 速 变 化 范 围 为0.2~1.6 m·s−1,Reynolds数的变化范围为2160~39600。
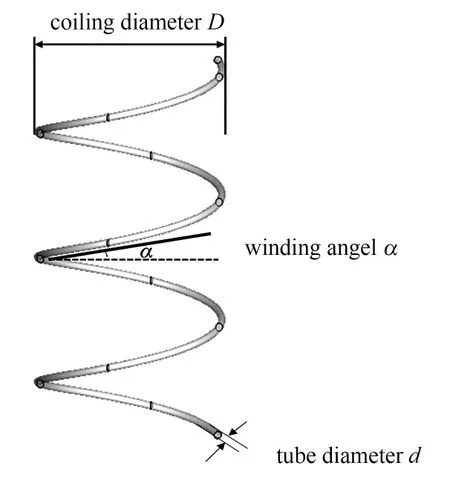
图2 缠绕管结构示意图Fig.2 Geometric parameters of a helical coil

表1 缠绕管的结构参数Table 1 Structural parameters of helical coils
以饱和KCl 溶液作为示踪剂,采用脉冲示踪法和电导率仪测量缠绕管内的液体停留时间分布曲线。实验步骤如下:(1)调节缠绕管内液体流量至指定流量并稳定10 min;(2)在t=0 时刻,将一定体积(5 ml)的饱和KCl 溶液通过注入装置加到缠绕管;(3)在缠绕管出口使用电导率仪实时记录电导率值。随着KCl 溶液不断流出,缠绕管出口处液体的电导率k(t)先上升,达到最大值kmax后开始下降,当所有的KCl 溶液从缠绕管出口流出时,k(t)趋于稳定并接近初始值,记为kmin;(4)改变实验条件,继续进行实验。
为了消除背景流体(水)的电导率对实验结果的影响,对k(t)进行归一化处理,得到无量纲的电导率k′(t)。

由k′(t)可计算得到相应的停留时间分布密度函数E(t):

对E(t)进行分析得到平均停留时间-t:



2 实验结果与讨论
2.1 直管中σ2随Re的变化
无量纲方差可以描述管内流体的混乱程度,在理想的平推流反应器中,σ2=0,说明管截面上的速度几乎完全相等;在全混流反应器中,σ2=1,说明管截面上的速度无序分布。因此,本文测量不同Re下直管(d=15 mm,长度l=4.6 m)中的液体停留时间分布,作为对比例。利用式(1)~式(5)计算σ2,σ2与液体Re 的关系如图3 所示,随着Re 的增加,σ2逐渐降低并趋向于平稳。在本文的实验条件下,直管中Re的变化范围是3000~20000,表明管中流体均处于湍流状态,传质受到对流和湍流扩散的双重影响,导致直管出口截面的σ2随Re 的增加而降低并逐渐趋向于0。这与文献所示的直管中流体流动的基本规律[23]一致,证实了实验装置和方法的可靠性。
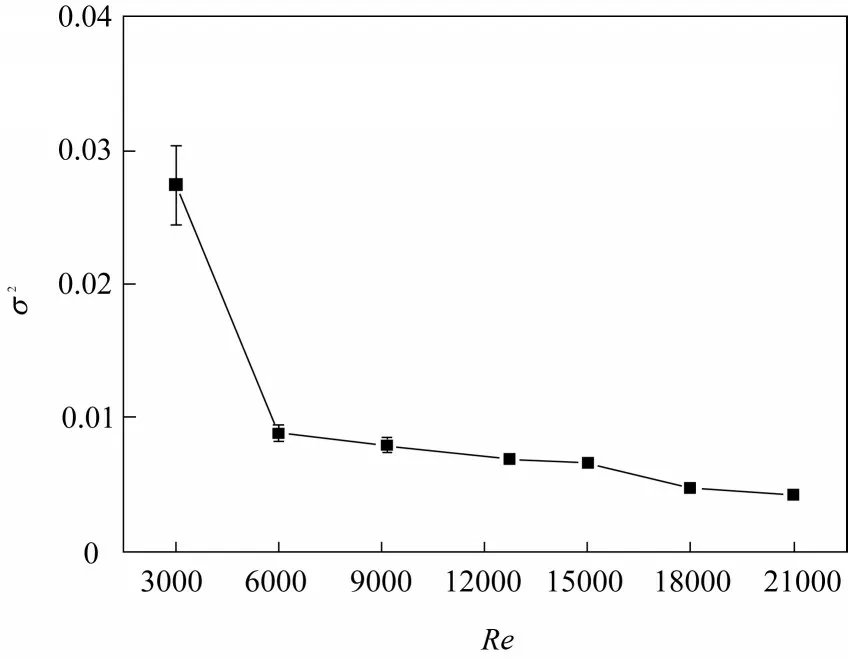
图3 直管出口σ2随Re的变化Fig.3 Variation of σ2 with Re in the straight pipe(d=15 mm,l=4.6 m)
2.2 不同结构缠绕管中σ2随Re的变化
利用上述实验方法,对不同Re下具有不同结构参数的缠绕管测量其RTD 曲线,并计算缠绕管出口处的无量纲方差σ2。在相同缠绕角度(α)和管径(d)下,不同缠绕直径(D)的缠绕管出口σ2随Re 的变化如图4 所示。随着Re 的增大,σ2呈先减小再增加的趋势,这与直管有较大的差异。当Re小于临界Reynolds 数ReS(图4 中曲线极小值点)时,σ2随着Re的增大而减小,这与直管中的结果一致,表明在Re较小时,缠绕管内的流体仍主要受与直管中类似的湍流效应影响。随着Re的增加,σ2呈下降趋势并逐渐趋向于0,此时湍流效应的影响逐渐减弱,管内流体流动逐渐趋于理想平推流。当Re 大于ReS时,管内流体在离心力的作用下产生较强的二次流,导致管截面速度的径向差异增大,管内流动逐渐远离理想平推流,从湍流作用区转变至二次流作用区。在二次流作用区,随着Re 的继续增大,管内流体的离心力增大,管内二次流逐渐增强,对应的σ2逐渐增大。这与Greenspan[17]的研究结果一致,然而文献中并没有发现在足够低的Re 下存在与直管中一致的湍流效应。
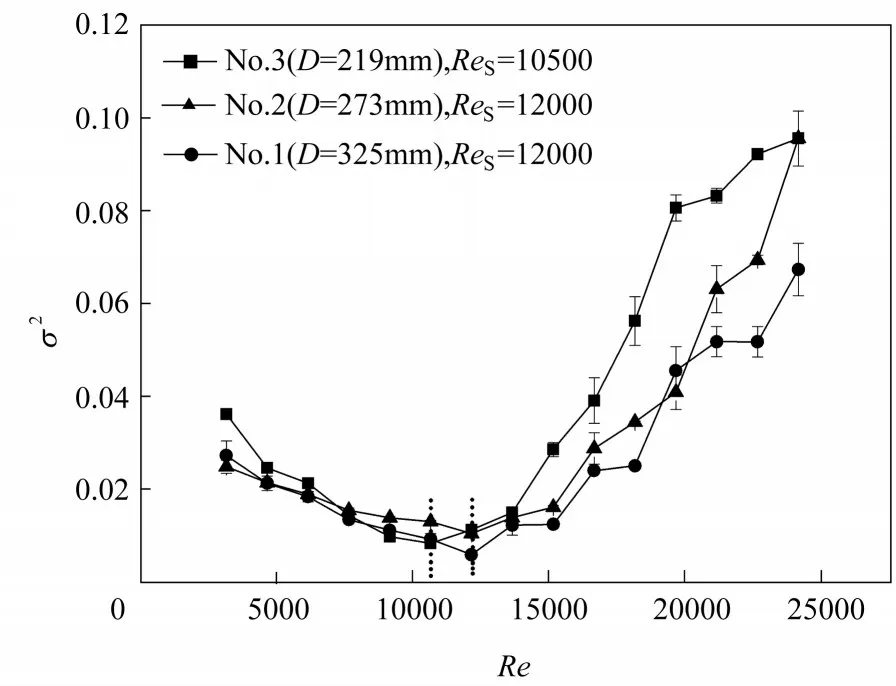
图4 不同缠绕直径的缠绕管出口σ2随Re的变化Fig.4 Variation of σ2 with Re in helical coils with different coiling diameters(α=10°,d=15 mm,l=4.6 m)
从图4还可以看出,当缠绕管的管径相同时,在Re 较低的区域,湍流效应对流体流动的影响差异较小,因此相同Re下测得的不同缠绕管出口σ2没有明显差异。在Re较高的二次流作用区,管内流体微元受到的离心力与缠绕直径呈反比,即缠绕直径越小,流体受离心力的影响越大,二次流强度越大,因此σ2越大,ReS越小。其中,缠绕直径为219、273 和325 mm 的 缠 绕 管 的ReS分 别 为10500、12000 和12000。这与Jayakumar 等[19]模拟得到的缠绕直径对缠绕管传热系数的影响规律一致。他们研究发现二次流会促使管内流体强烈再循环和混合,使得对流传热系数增加;同时,随着缠绕直径的增加,二次流的影响逐渐减弱,对流传热系数减小。可见,缠绕直径越小,二次流对缠绕管传热的影响越大。
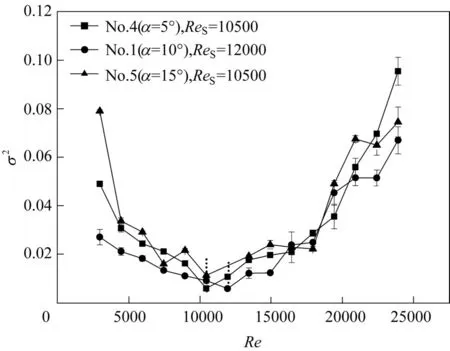
图5 不同缠绕角度的缠绕管出口σ2随Re的变化Fig.5 Variation of σ2 with Re in helical coils with different coiling angles(D=325 mm,d=15 mm,l=4.6 m)
在相同缠绕直径(D)和管径(d)下,不同缠绕角度(α)的缠绕管出口σ2随Re 的变化如图5 所示。与图4 类似,不同缠绕角度的缠绕管出口σ2随Re 的增加也呈现先减小再增加的变化规律。在二次流作用区,不同缠绕管中的二次流强度在相同Re下较为接近,即出口σ2几乎相同,这与Jayakumar 等[19]的传热模拟结果具有一致性。他们研究了缠绕角度对Nusselt 数的影响,发现当缠绕角度在8°~10°的范围内时,局部Nu 几乎相同,此时缠绕角度不会影响二次流的强度。可见,缠绕角度对缠绕管传热效率的影响较小,可以忽略。
在相同缠绕直径(D)和缠绕角度(α)下,不同管径(d)的缠绕管出口σ2随Re 的变化如图6 所示。当缠绕管的管径为11 mm 时,σ2随Re 的增加先减小后增大再趋于平稳;当管径为15 mm和22 mm时,σ2随Re 的增加先减小后增大,与图4 和图5 所示的规律相同。当缠绕管的管径为11、15 和22 mm 时,对应的ReS分别为5500、12000 和22000。可见,缠绕管的管径越小,ReS越小。这与Mirgolbabaei 等[34]的传热模拟结果一致,他们研究发现当管径增大时,缠绕管的换热效率降低,压降也随之减小。当缠绕管的缠绕直径和角度相同时,单位流体微元在径向上受到的离心力大小相同,即流体微元的径向加速度相同,在相同的流动时间内其在管道径向截面上的位移也相同。因此,缠绕管的管径越小,径向上流体相对位移越大,二次流作用越强。但是,流体在径向上的迁移距离受到管径的限制。在小直径的缠绕管中,当流体径向迁移距离达到极限时,缠绕管出口处的σ2不再随Re变化,对应的二次流强度达到极限,此时管内流体流动从二次流作用区转变为二次流极限区。由于实验条件的限制,本文仅在管径11 mm的缠绕管中发现了二次流极限区。

图6 不同管径的缠绕管出口σ2随Re的变化Fig.6 Variation of σ2 with Re in helical coils with different tube diameters(D=325 mm,α=10°,l=4.6 m)
2.3 缠绕管中流体流动的转变规律
不同结构参数的缠绕管中临界Reynolds数如表2 所示,其中ReS是从湍流作用区转变为二次流作用区的临界Reynolds 数,ReL是从二次流作用区转变为二次流极限区的临界Reynolds 数。由表可知,ReS随着缠绕直径(D)和缠绕管管径(d)的减小而减小,缠绕角度(α)对ReS没有影响。根据上述实验结果,构建了如图7 所示的缠绕管内流动特性示意图。在不同的操作条件下,缠绕管内会出现湍流作用区、二次流作用区和二次流极限区三种不同的流型。其中,Ⅰ区域为湍流作用区,缠绕管出口σ2随Re的变化规律与直管类似,缠绕管出口σ2随Re 的增大而降低;Ⅱ区域为二次流作用区,缠绕管出口σ2随Re 的增大而增大;Ⅲ区域为二次流极限区,缠绕管出口σ2随Re 的增大不再明显变化。当缠绕管内的径向流动未达到极限迁移距离时,随着Re 的增大,缠绕管中流体流动特征会从湍流作用区转变为二次流作用区;当缠绕管内的径向流动达到极限迁移距离时,缠绕管中的流体流动特征会从湍流作用区先转变为二次流作用区,再转变为二次流极限区。
3 结 论
(1)提出了通过测量缠绕管内液体的停留时间分布,利用无量纲方差σ2定量表征缠绕管内二次流强度的方法。
(2)考察了缠绕直径、缠绕角度、管径对缠绕管内二次流的影响规律。当缠绕管内的径向流动未达到极限迁移距离时,缠绕管出口σ2随着Re的增大先减小后增大,分别对应湍流作用区和二次流作用区,转变点为临界Reynolds 数ReS;当缠绕管内的径向流动达到极限迁移距离时,缠绕管出口σ2随着Re的增大先减小后增大再趋于平稳,分别对应湍流作用区、二次流作用区和二次流极限区,转变点分别为临界Reynolds数ReS和ReL。
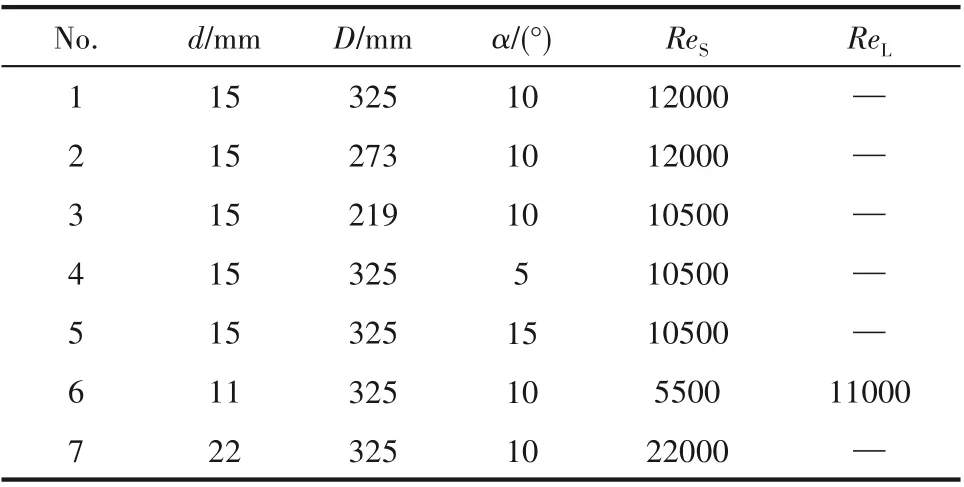
表2 不同缠绕管的临界ReS和ReLTable 2 ReS and ReL in different helical coils
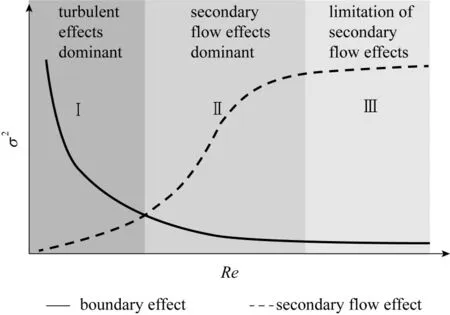
图7 缠绕管中流体流动特性示意图Fig.7 Schematic diagram of the fluid flow characteristics in helical coils
(3)从湍流作用区转变为二次流作用区的临界Reynolds 数ReS随缠绕直径和缠绕管管径的减小而减小,缠绕角度对ReS的影响较小。
