一种三自由度并联机构误差分析与补偿

张吉旺，宋胜涛，李瑞琴

(中北大学机械工程学院，山西 太原 030051)

导致并联机构存在误差的原因有很多种，如驱动副固有误差、零件制造误差和安装误差等。

有很多学者对误差建模、误差分析和误差补偿进行了研究。单鹏等[1]通过D-H矩阵法对Stewart型并联机床进行了误差建模和误差分析，发现当并联机床位姿要求高时，在误差分析中应考虑杆件的全部D-H参数；杨斌[2]通过D-H矩阵法对3-RSR并联机构进行了误差建模和误差分析，最终以补偿杆长固有误差的方法减小动平台的位姿误差；He 等[3]用D-H矩阵法对三自由度并联机械手建立了误差模型并进行了精度分析；陈小岗等[4]对6-UPS并联机床的误差分布特性进行了研究，给出了在不同位姿下的误差比值；Akhbari 等[5]将实际运动轨迹和理论预测轨迹相比较，分析了四自由度并联机床的运动精度；Sun 等[6]对一移三转的并联机构进行几何精度设计和误差分析，降低了3个转角的误差；房立金等[7]对带有约束的3-TPS并联机床进行位姿误差分析，通过蒙特卡洛法对误差结果进行统计，发现来自机床内部约束的误差对末端执行器误差的影响最大；Tian 等[8]对五自由度并联机床的病态位置进行误差分析，避免了并联机床出现病态位置；Zhao 等[9]对六自由度并联机床进行误差分析并降低了误差；安守和等[10]对两操作模式2-R(SS)2-R(RR)2(RR)2并联机构进行了误差分析及精度设计，通过算例在给定误差精度的条件下找到了最佳制造误差值；曾达幸等[11]提出了一种少自由度并联机构的误差分析方法，通过试验样机验证了该方法的正确性。也有学者通过粒子群算法求解出优化目标的最优解。侯雨雷等[12]用粒子群算法对3PSS/S并联机构进行误差补偿，使动平台的运动误差下降了40%左右；李冰冰[13]以Stewart六自由度并联机器人为研究对象，用粒子群算法找出杆长误差尺寸的最优解，最大程度补偿了机构动平台的位姿误差。

本文以移动副驱动的三自由度并联机构为基础，通过控制零件制造误差的方式来补偿移动副固有误差带来的动平台位姿误差。

1 并联机构的误差模型建立

1.1 并联机构简介

本文的并联机构如图1所示。整个并联机构由定平台、动平台和3条支链组成。支链1和支链2为PRU支链，由1个P副(移动副)、1个R副(转动副)和1个U副(万向铰)组成。支链3为闭环球铰支链，由1个P副、4个S副(球副)的闭环球铰和1个R副组成。在定平台上的坐标系OA-XAYAZA为定坐标系；在动平台上的坐标系OB-XBYBZB为动坐标系。

该并联机构有3个自由度，分别为沿YA和ZA轴的移动和绕YA轴的转动。相对于其他的三自由度并联机构，该并联机构属于非对称结构，支链3为适应性中央支链，不仅可以增加并联机构的刚度，还可以增加并联机构的驱动力。支链3为P-2(SS)结构，这种闭环球铰结构相对于其他的结构，可以给动平台提供较大的转角。

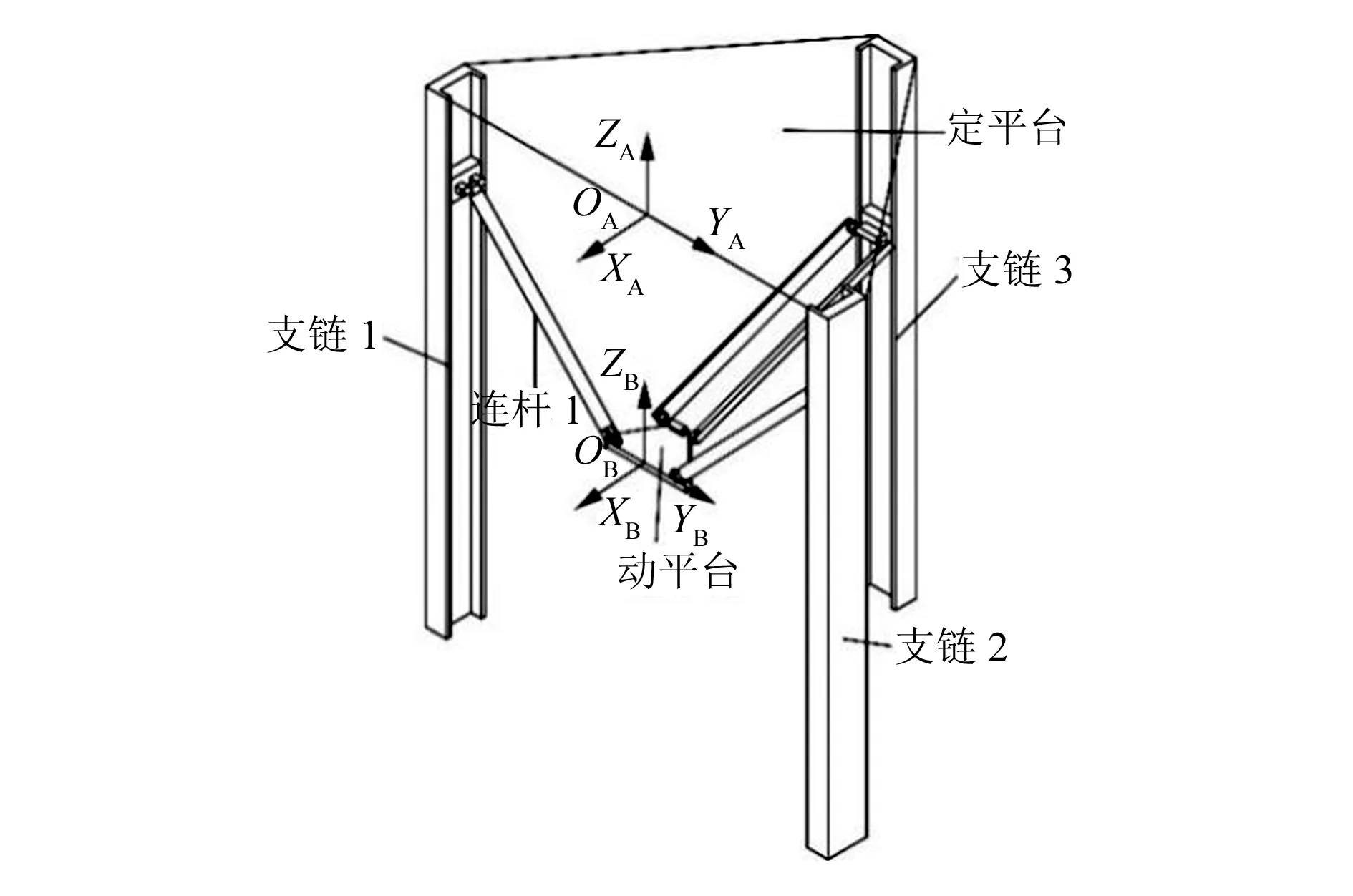
图1 并联机构的模型图

1.2 并联机构误差建模

该并联机构的位置反解[14]如式(1)所示：

(1)

式中：d1，d2，d3为移动副的位移，为了满足该并联机构的运动要求，三者均取正值；y，z分别为动平台在定坐标系下的YA，ZA方向的位置；L为并联机构的连杆长度；R为定平台外接圆半径；r为动平台外接圆半径；θ为动平台绕YA轴转动的角度；s，c分别表示sin和cos。

由位置反解可得位置正解，如式(2)所示：

(2)

对式(2)进行全微分，得到该并联机构的误差模型，如式(3)所示：

(3)

式中：δy,δz,δθ为动平台位姿误差；δr,δR,δL为零件制造误差；δd1,δd2,δd3为移动副固有误差。

2 并联机构的误差分析

该并联机构r=130 mm，R=590 mm，L=780 mm。为了使零件的配合性质比较稳定，故并联机构主要部件的制造精度为IT5。在此制造精度下，经查手册，动平台、定平台和连杆的制造误差分别为δr=±0.009 mm，δR=±0.016 mm，δL=±0.018 mm[15]。由于电缸导致移动副的位移d1，d2和d3存在固有误差，因此假设为δdi=±0.01 mm(i=1,2,3)，并联机构的零件制造误差呈正态分布。由于零件的制造误差具有随机性，因此用MATLAB进行编程仿真，具体思路如图2所示。

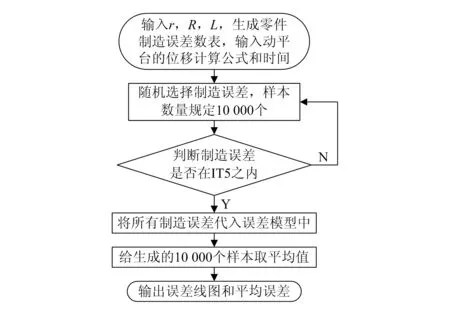
图2 误差仿真逻辑框图

2.1 位移误差分析

动平台位移计算公式如式(4)所示，输入动平台转动时间t为30 s。最终仿真结果如图3和图4所示。

(4)

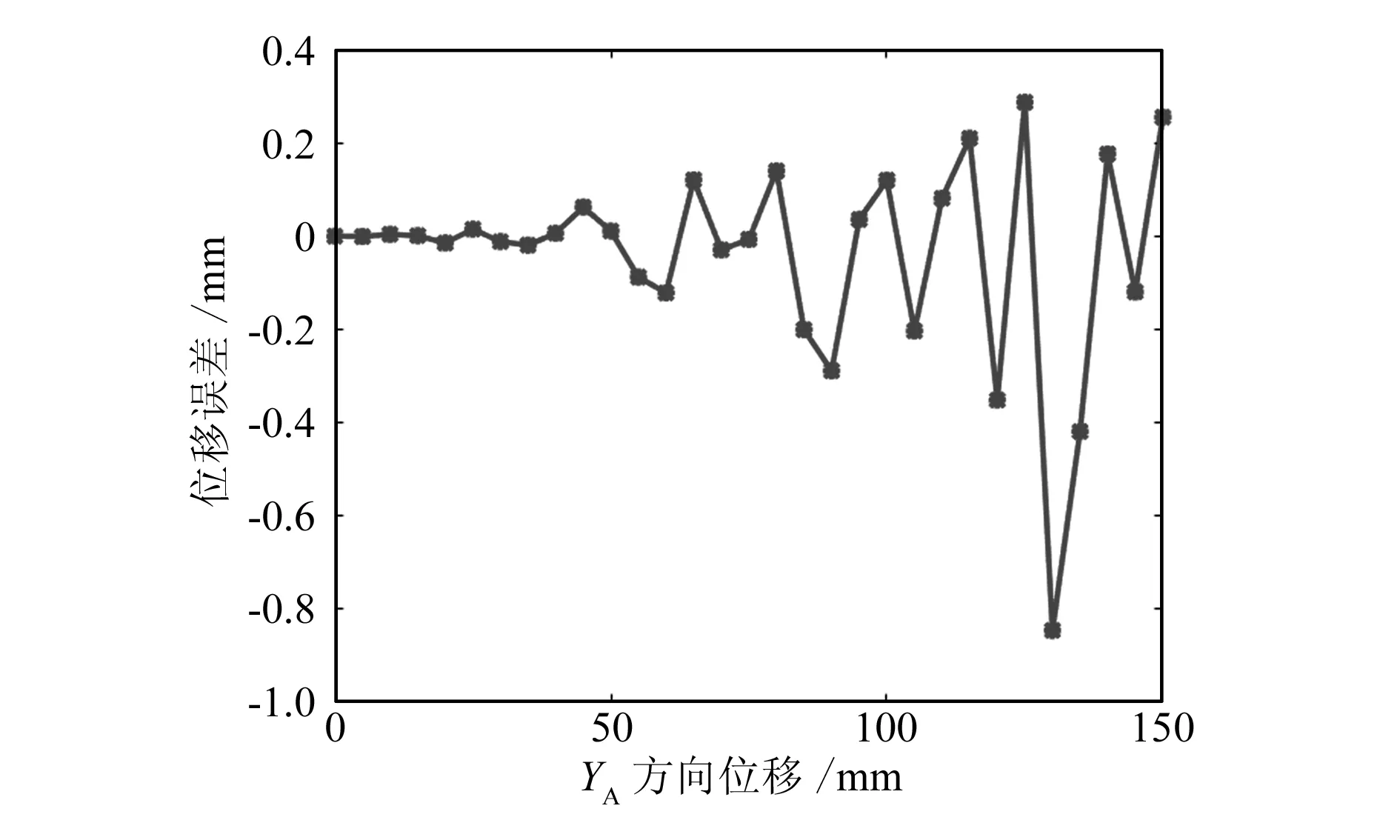
图3 YA方向位移误差仿真结果

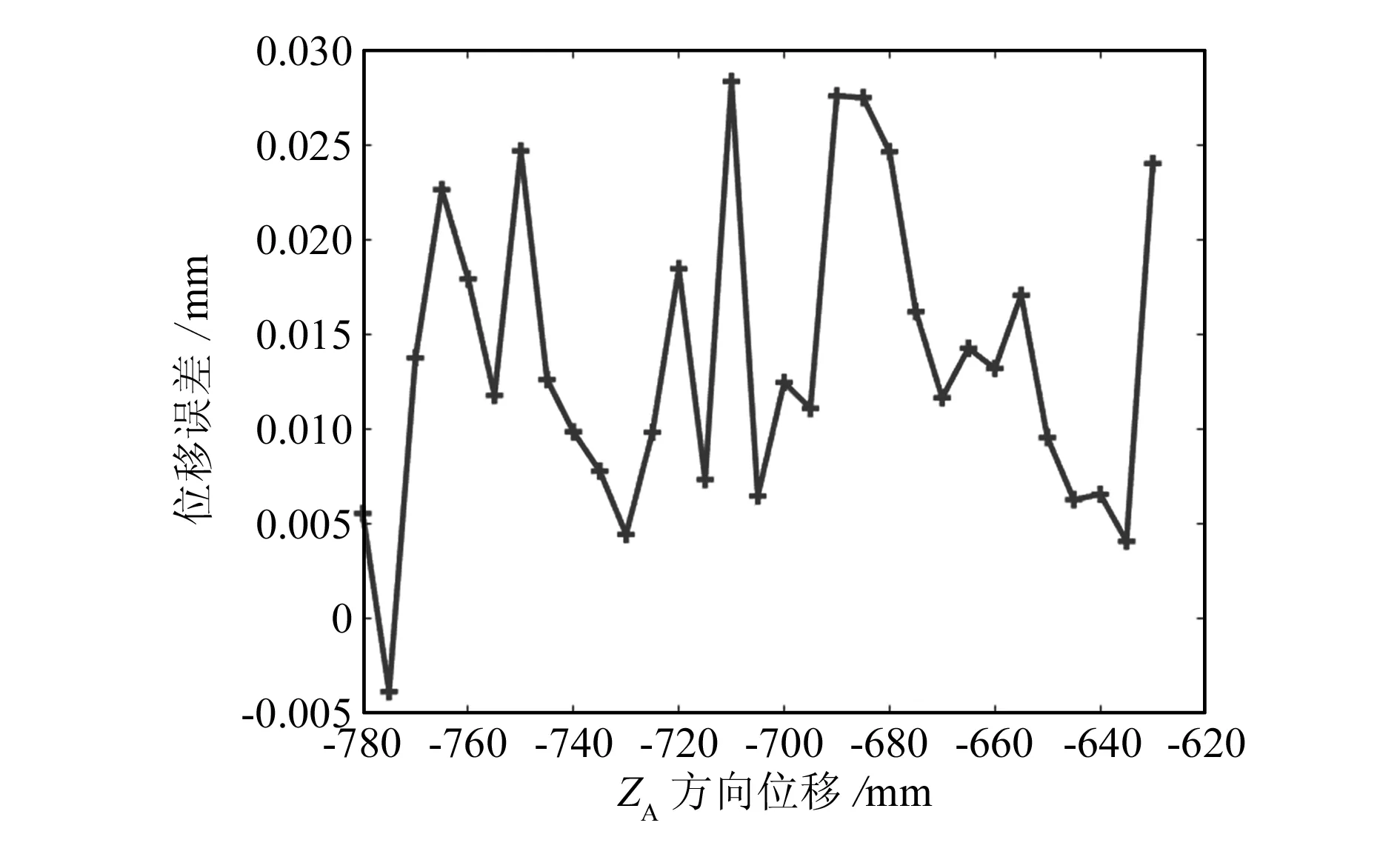
图4 ZA方向位移误差仿真结果

2.2 转角误差分析

动平台转角计算公式如式(5)所示，输入动平台转动时间t为30 s。最终仿真结果如图5所示。

(5)

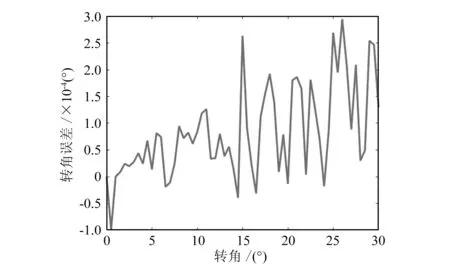
图5 绕YA轴转角误差仿真结果

由图5可知，虽然曲线的波动较大，但是绕YA轴的转角误差较小，几乎对动平台的转角没有影响，因此可以忽略不计。

3 并联机构的误差补偿

3.1 用粒子群算法求解固定误差的最佳制造误差

首先定义适应度函数如式(6)和式(7)所示：

(6)

F=|f1|+|f2|+|f3|

(7)

式中：f1，f2，f3分别为δy，δz，δθ的适应度函数；F为目标函数的收敛值。

在粒子群算法中，把式(7)作为目标函数。当F越接近于0，证明求解的结果越精确。通过采用粒子群算法完成MATLAB编程，给定算法的迭代次数为500次。在迭代约240次后出现收敛，F=0.003 55，如图6所示。由于粒子群算法解方程得出满足条件的结果并不唯一，因此最终取出误差补偿效果较好的10组解做详细分析，见表1。

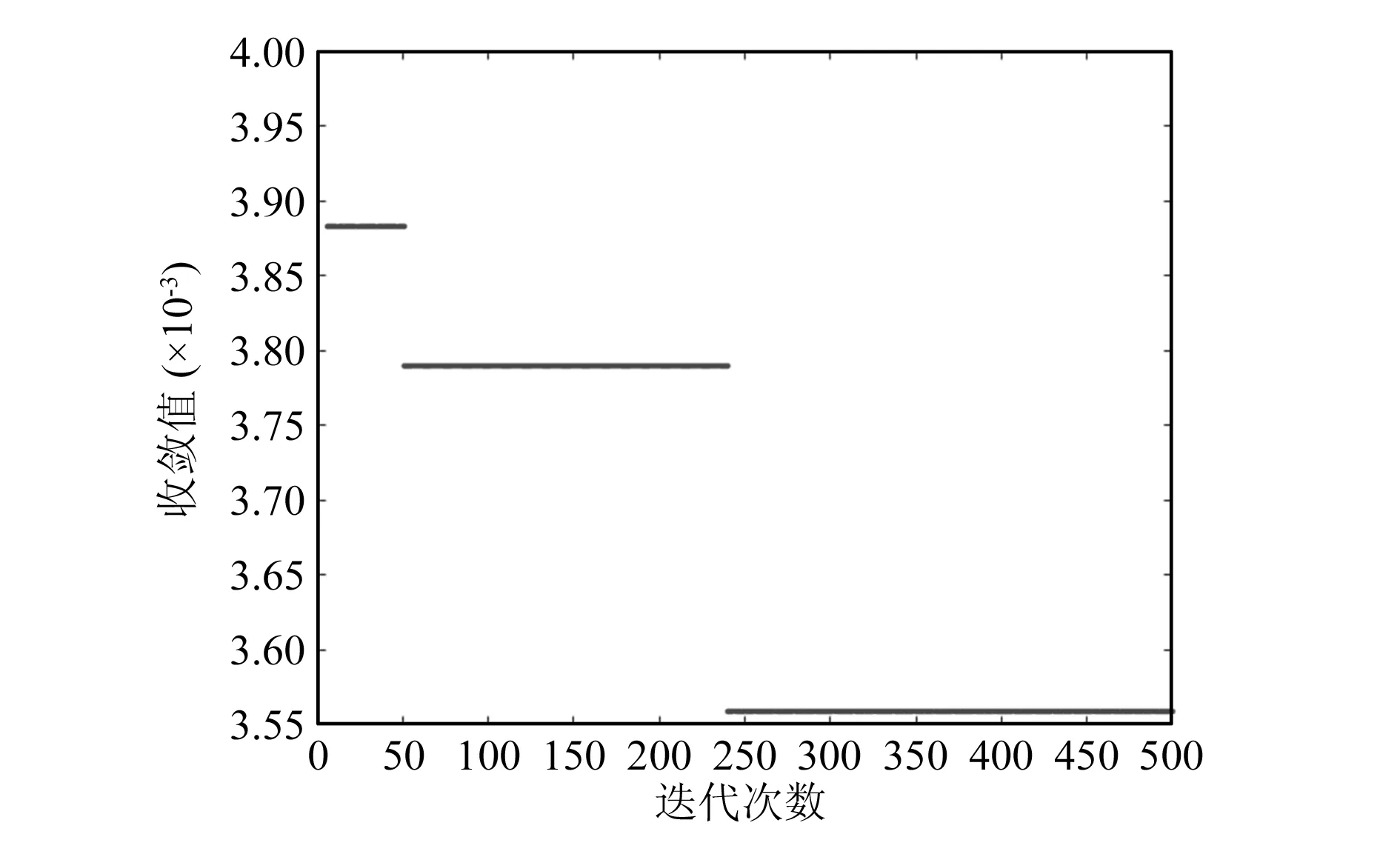
图6 粒子群算法目标函数收敛值变化图

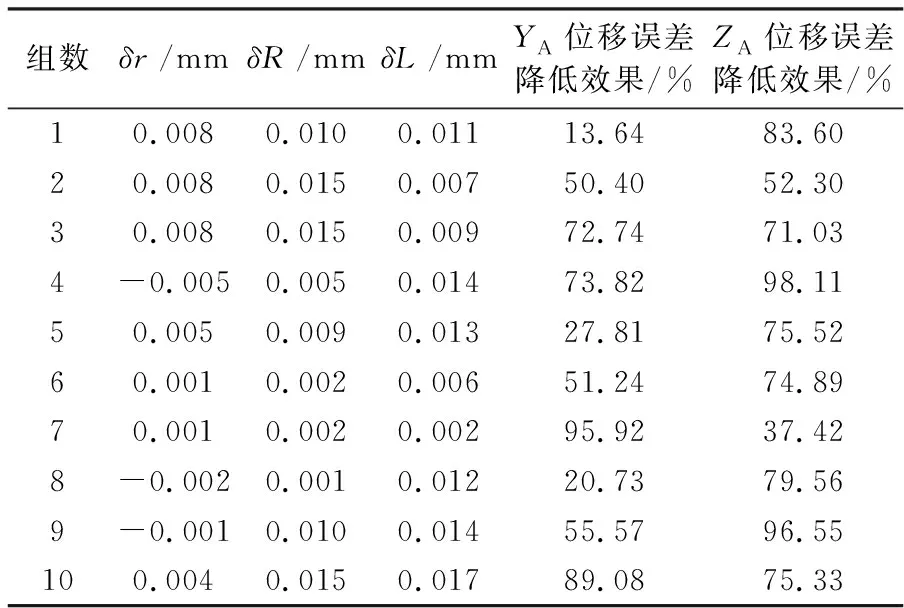
表1 不同组合的零件制造误差对YA，ZA位移误差的降低效果

3.2 误差补偿结果

在表1中选择第7组较优解为例，代入MATLAB中再次仿真，结果如图7和图8所示。

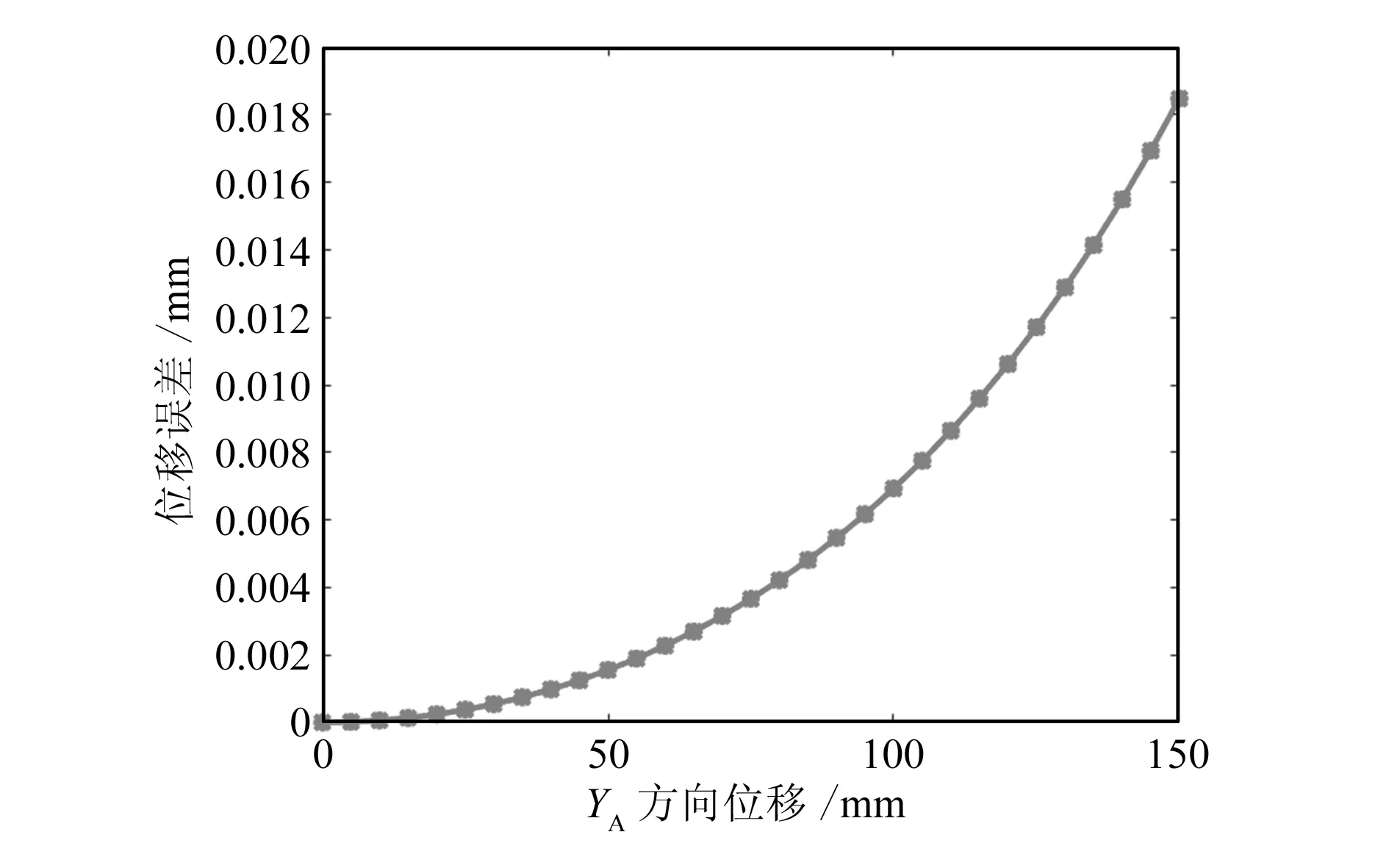
图7 误差补偿后YA方向位移误差仿真结果

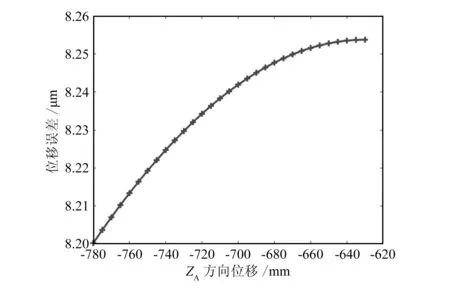
图8 误差补偿后ZA方向位移误差仿真结果

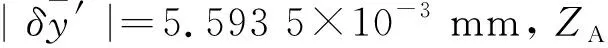
4 结束语

本文分析了2-PRU-P-2(SS)并联机构的位移误差和转角误差。结果显示，该机构位移误差较大，需要优化补偿；转角误差较小，不需要优化补偿。由于沿YA方向的位移误差比沿ZA方向的位移误差大，因此在最终误差补偿的仿真过程中，可选择沿YA方向位移误差补偿效果明显的一组制造误差。由于电缸导致移动副位移存在固有误差，通过粒子群算法，以控制零件制造的方式对动平台的位姿误差进行补偿。补偿之后，动平台沿YA的位移误差最高可减少95.92%，沿ZA的位移误差最高可减少98.11%。