高放大率柔性微夹钳的优化设计与分析

周烁方，赵世瑾，康升征，吴洪涛

(1.南京航空航天大学机电学院，江苏 南京 210016) (2.南京航空航天大学电子信息工程学院，江苏 南京 211106)

随着微/纳米技术的不断发展，研究对象逐渐趋于微细化，显微操作技术应运而生并成为国内外学者研究的核心方向[1]。显微操作技术主要用于操纵尺寸微小的物体，在精密光学[2]、生物医学[3]、微装配[4]和微细加工[5]等领域得到广泛应用。微夹钳作为显微操作系统的关键设备，在学术领域和工业应用领域备受关注。

压电作动器因其具有刚度高、分辨率高、能量密度高、响应速度快和驱动力大等优点[6]，被广泛用于微夹钳和高精度定位系统。压电作动器输出位移比较小，通常约为长度的0.2%[7]。因此，需要使用位移放大机构对压电作动器的输出位移进行放大。相比传统的机械传动机构，柔性机构具有无运动间隙、无摩擦、不需要润滑、输入输出呈线性、一体化结构等优点[8]。因此，本文基于柔性机构设计位移放大机构。

由于微小物体通常尺寸跨度大(从1 μm到1 mm)[7]，因此对微小物体进行操作的微夹钳的夹持行程需涵盖1 μm～1 mm。此外，在实际夹持操作中，微小物体通常是球形或不规则形状，这就要求微夹钳末端在夹持运动中不能含有偏转位移。

目前，已有大量学者对微夹钳开展了研究。文献[7]、[9]～[12]中所提出的微夹钳均采用两级放大机构，最大位移放大率为21.4倍，夹持行程仅为427.8 μm。Wang等[13]设计的微夹钳虽实现了三级放大，但其夹持行程仅为190 μm。目前，众多文献中提出的微夹钳均不能满足大尺寸微小物体(427.8 μm及以上)的操作需求。

由于目前已经提出的微夹钳均不能采用平动夹持的方式对大尺寸微小物体进行稳定夹持操作，因此笔者设计了一种同时具备高位移放大率、大夹持行程和平动夹持等特点的新型微夹钳。该微夹钳采用平行四边形机构直接与末端连接，保证微夹钳平动夹持，提高了夹持稳定性。

1 微夹钳构型设计与运动分析

1.1 构型设计

本文所设计的新型微夹钳如图1所示。微夹钳由压电作动器、运动放大机构、抓爪和基座组成。运动放大机构包含杠杆机构、Scott-Russell机构和平行四边形机构。两个预紧螺钉用于调节预紧力。抓爪通过平行四边形机构直接连接到固定基座上，隔绝寄生偏转运动，保证微夹钳末端输出为纯粹平移运动。

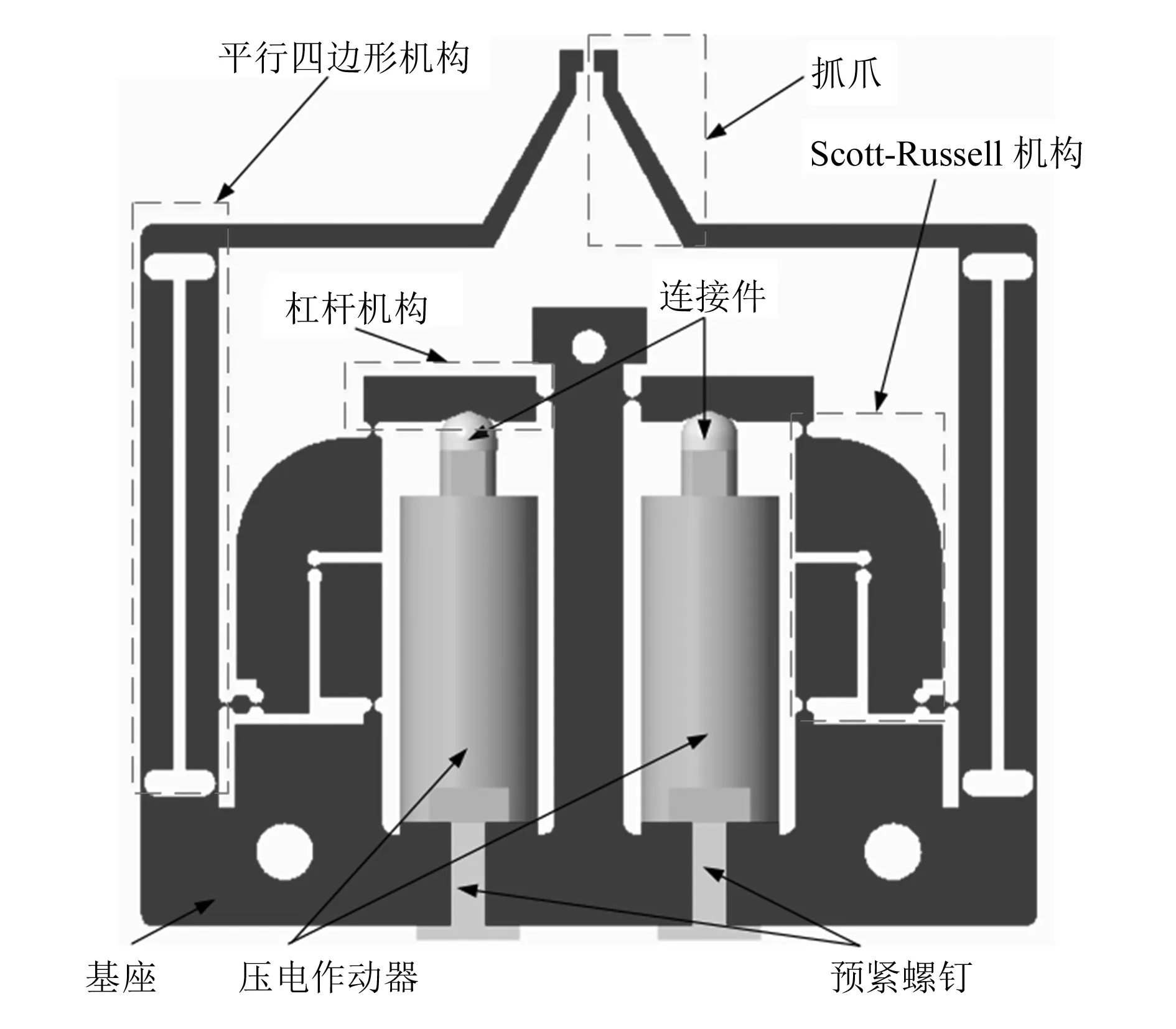
图1 微夹钳示意图

微夹钳呈常开状态，通过压电作动器的伸缩运动实现夹持和释放动作。压电作动器外加电压时，在微夹钳输入端会产生驱动位移。输入位移经由杠杆机构实现第一级放大；再通过Scott-Russell机构进行二级放大并传递给平行四边形机构；最后由平行四边形机构保证微夹钳输出为纯移动，并实现微夹钳第三级放大。

1.2 运动分析

根据伪刚体模型可知，柔性铰链可以等同于一个带有扭转弹簧的理想单轴旋转关节[14]。运动学分析时，将柔性铰链连接的连杆视为刚体。由于微夹钳结构是对称分布的，因此本文仅选取其一半进行分析，如图2所示。图中O,A,…,I表示柔性铰链的旋转中心，a,b,…,k表示微夹钳的几何参数。Scott-Russell机构连杆需等长[15]，即LCD=LDE=LDF。图3和图4分别给出了微夹钳的运动矢量和角度变化。在图3中将微夹钳的三级运动放大机构拆分成3个简单的连杆机构，以简化分析。在图4中Pin，dx分别表示微夹钳的输入位移和输出位移，位移放大率用λ表示，它们之间的关系可用式(1)表示：

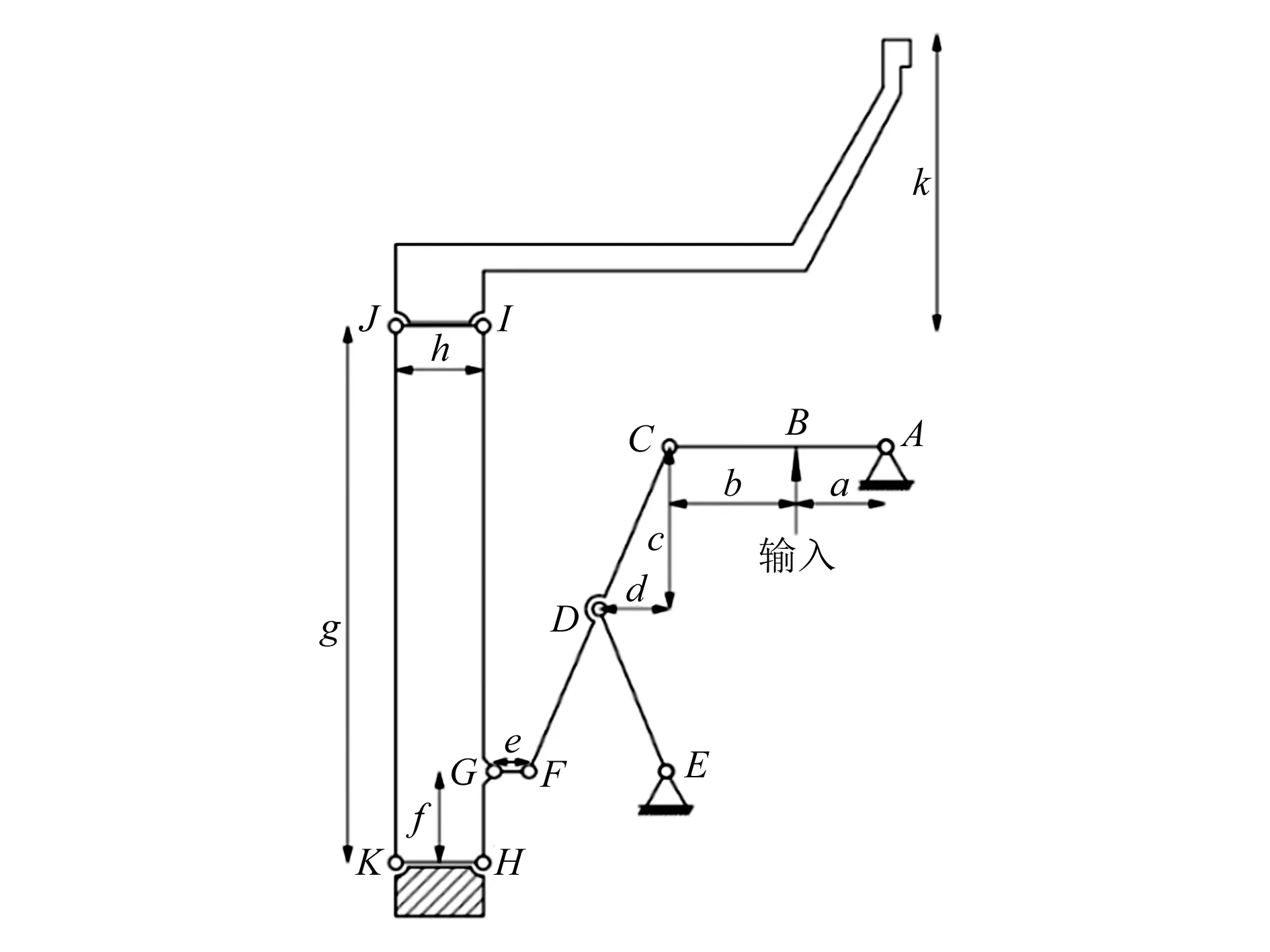
图2 微夹钳几何参数

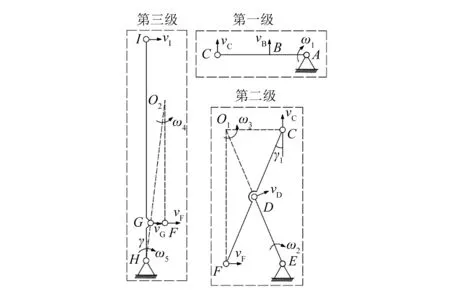
图3 微夹钳运动矢量

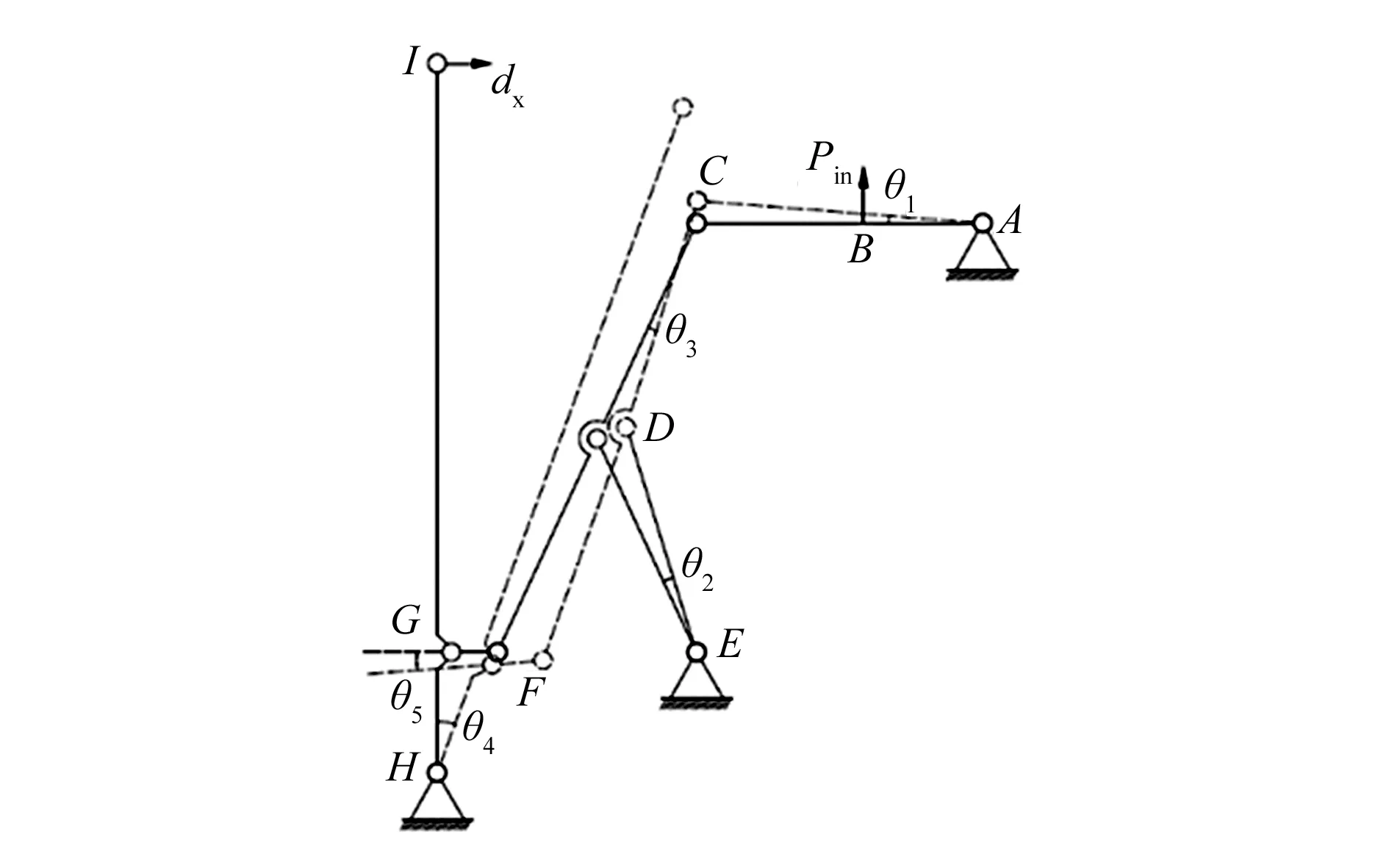
图4 微夹钳位移及角度变化

dx=λpin

(1)

点B和C的瞬时速度vB和vC分别为：

vB=ω1LAB

(2)

vC=ω1LAC

(3)

式中:ω1为杆AC的角速度;LAB和LAC分别为点A到点B,点A到点C的距离。

因此，由式(2)和式(3)得到杠杆机构的位移放大率λ1为：

(4)

通过C点和F点速度方向的垂线交点确定连杆CF的瞬时中心O1。点C和F的瞬时速度表达式如下：

vC=ω3LO1C

(5)

vF=ω3LO1F

(6)

式中:ω3为杆O1C的角速度；LO1C和LO1F分别为点O1到点C，点O1到点F的距离。

因此，由式(5)和式(6)得到Scott-Russell机构的位移放大率λ2为：

(7)

同理，点F，G和I的瞬时速度为：

vF=ω4LO2F

(8)

vG=ω4LO2G=ω5LGH

(9)

vI=ω5LHI

(10)

式中：ω4为杆O2F的角速度；ω5为杆GH的角速度；LO2F,LO2G,LGH和LHI分别为点O1到点F，点O2到点G，点G到点H，点H到点I的距离。

由式(8)、式(9)和式(10)得到平行四边形机构的位移放大率λ3为：

(11)

联立式(1)、式(4)、式(7)和式(11)可获得微夹钳的位移放大率λ：

(12)

连杆GH和HI所成的角度γ可由下式求得：

(13)

式中：rG为G点的铰链半径；tH为点H处的铰链厚度。

根据图4可知，输入位移为Pin时，连杆的角度增量为θ1～θ5，柔性铰链A,C～K的旋转角αA,αC～αK为：

(14)

(15)

(16)

(17)

(18)

(19)

式中负号表示柔性铰链沿顺时针方向转动。

2 力学建模与优化

2.1 静力学模型

微夹钳的静力学模型就是利用伪刚体模型近似描述柔性铰链力与转动的关系[16]。柔性铰链可以等效替换为具有扭转弹簧的单自由度旋转关节，只要将柔性铰链的几何参数与扭转刚度k相关联即可。微夹钳中使用了两种柔性铰链，其中杠杆机构、Scott-Russell机构及其连接处的柔性铰链为双切口直圆柔性铰链，平行四边形机构采用了单切口直圆柔性铰链。使用文献[17]、[18]中推导出的铰链参数和铰链刚度的公式：

(20)

(21)

式中：ki为铰链刚度；E为材料的弹性模量；参数n,ti和ri分别为柔性铰链的宽度、厚度和半径。

微夹钳输入力Fin和输入位移Pin之间的关系：

Fin=kinPin

(22)

式中：kin为微夹钳的输入刚度。

根据上述关系，可以将静力学问题转化为对结构的输入刚度kin的求解。根据虚功原理得到：

(23)

式中：δW为总功；等号右侧第一项表示由输入力产生的虚功为正功；第二项表示输出力产生的虚功为负功；其中Fout为微夹钳输出力；第三项表示由铰链上的转矩产生的虚功为负功，其中αi为柔性铰链A～J的旋转角；Mi为第i个铰链产生的转矩。

Mi=kiαii=A,C,…,K

(24)

为了分析各个柔性铰链的应力情况，需要确定各个柔性铰链的反作用力和扭矩，受力分析如图5所示。对各个刚性连杆进行静态平衡分析，得到以下公式：

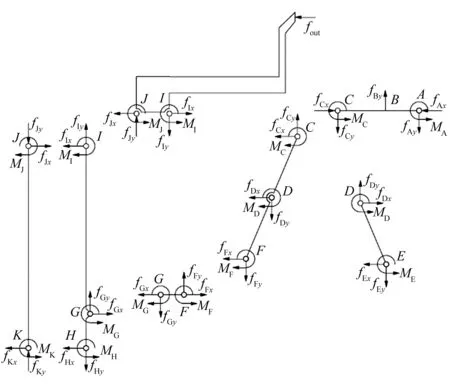
图5 微夹钳静力分析

fBy=fin

(25)

(26)

(27)

(28)

(29)

(30)

fAx=fCx=-fDx-fFx

(31)

(32)

fHy=fIy+fGy

(33)

最大应力σmax通常出现在柔性铰链的最薄区域的外表面处，并且是在弯曲和拉压复合作用下产生的，即：

(34)

(35)

(36)

柔性铰链的最大应力应小于许用应力：

(37)

式中:[σ]为材料的屈服强度；Sσ为安全系数。

2.2 动力学模型

由于微夹钳使用柔性铰链，不存在摩擦，因此可以认为系统没有阻尼[19]。本文采用q=[q1q2]T描述微夹钳平面运动。利用拉格朗日方程建立动力学模型：

(38)

式中：L为拉格朗日量；qi为广义坐标；Fi为广义力。其中拉格朗日量L可以表示为：

L=T-V

(39)

式中：T为微夹钳各个运动臂的动能之和；V为微夹钳中各铰链的势能之和。

T的表达式为：

(40)

式中：JAC,JDE,JCF,JFG和JHI表示连杆AC,DE,CF、FG和HI的转动惯量；mout为微夹钳输出端的质量。

V的表达式为：

(41)

联立式(2)～式(12)和式(38)～式(41)可得系统的动力学方程：

(42)

式中：M,K和F分别为微夹钳的等效质量、等效刚度和广义力。因此，系统的固有频率fn为：

(43)

2.3 参数优化

本文选择柔性铰链参数t和r作为优化设计变量对微夹钳固有频率进行优化。首先使用ANSYS软件进行预分析以判断所设计的微夹钳振动情况，微夹钳使用表1参数，柔性铰链参数取t=0.3 mm、r1=r2=0.5 mm、r3=0.8 mm。结果表明一阶振动方向即为夹持运动方向，因此选择一阶频率函数f作为优化目标函数。

表1 微夹钳参数

优化设计过程可描述为：

1)设计变量。

X=[x1x2x3x4x5x6]=[r1r2r3t1t2t3]，其中变量t1和r1对应A点铰链参数，t2和r2对应C,D,E,F,G点铰链参数，t3和r3对应H,I,J,K点铰链参数。

2)优化目标。

最大化一阶固有频率O(X)=max[f1(x)],其中f1(x)为一阶固有频率。

3)约束条件。

①尺寸约束。变量取值范围分别为

0.5 mm≤xi≤1.0 mmi=1,2

0.8 mm≤x3≤1.5 mm

0.2 mm≤xi≤0.5 mmi=4,5,6

②刚度约束。微夹钳性能受输入刚度kin影响，如果输入刚度过大会降低压电作动器的输出，此处取kin≤0.1kPZT，其中kPZT为压电作动器刚度。

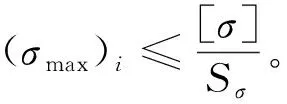
本文采用MATLAB优化工具箱进行优化，赋予优化初值X=[x1x2x3x4x5x6]=[0.5 0.5 0.8 0.2 0.2 0.2]，优化结果为r1=0.8 mm、r2=0.7 mm、r3=1.2 mm、t1=t2=t3=0.2 mm、kin=1.09 N/μm、f1=98.51 Hz。

3 有限元仿真分析

下面通过有限元仿真来验证上述所建的运动学、静力学和动力学模型的准确性。根据图2所示的几何模型建立有限元仿真模型，用于研究微夹钳的运动行程、应力分布、刚度和动态性能等。在微夹钳输入端施加19 μm的输入位移验证最大行程，结果如图6所示，最大输出位移为517 μm。从图6(b)中可以得出，沿Y方向的寄生运动为7.17×10-4mm，运动耦合比仅为0.14%。

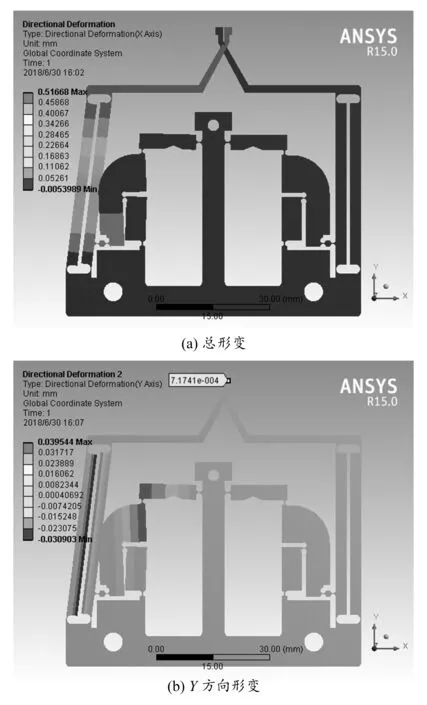
图6 静态分析结果

通过有限元仿真得出微夹钳输入刚度为1.34 N/μm，而理论模型计算得出输入刚度为1.09 N/μm，与有限元分析结果相比偏差为18.7%。在运动过程中微夹钳的应力分布情况在图7中给出，由图可知，应力集中现象仅发生在柔性铰链处，最大应力为244.26 MPa，小于许用应力251.5 MPa(Sσ=2)。前6阶固有频率见表2。理论模型计算得出的1阶固有频率为98.51 Hz，与模态分析得出的114.01 Hz相比相对误差小于13.6%。

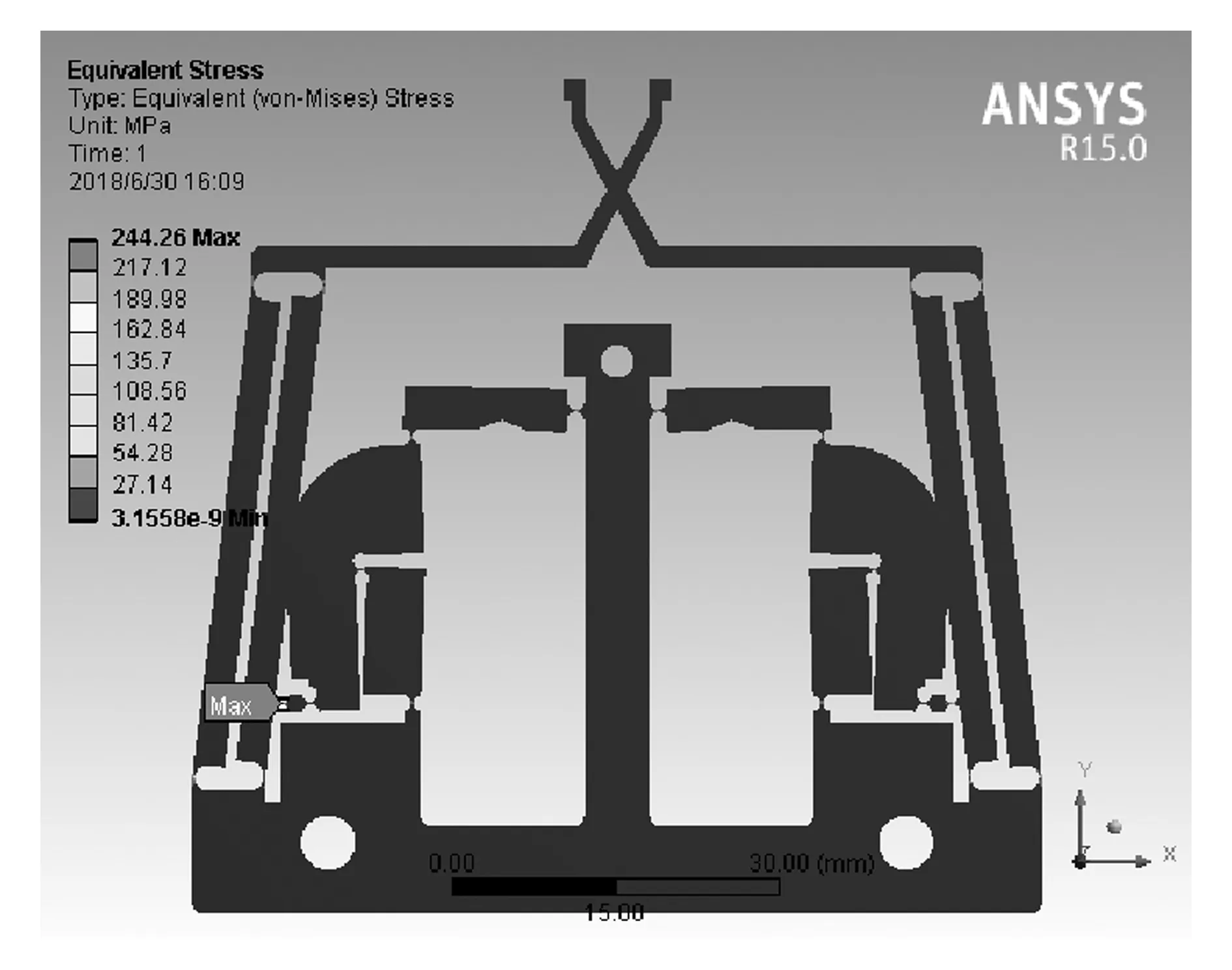
图7 应力分布分析

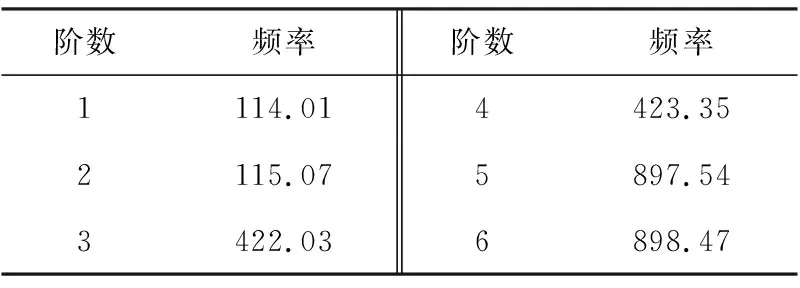
表2 微夹钳模态频率 单位:Hz

4 实验测试

下面通过实验对设计的微夹持器及其运动模型进行验证，搭建的实验装置如图8所示。机械结构主要由微夹钳、压电作动器和激光位移传感器组成。压电作动器(型号Pst120/7/20VS12)通过螺钉预紧，采用电压放大器驱动。激光位移传感器(型号LK-H022)通过信号调节器(型号LK-G5001)输出电压信号，然后通过数据采集卡(型号PCI-6229)的A/D通道获取电压，控制信号由D/A通道产生，最后由电压放大器放大12倍驱动压电作动器实现夹持操作。为减少外部振动干扰，整个实验装置安装在振动隔离台上。

图9总结了3种方法得到的输出位移与输入位移之间的关系，其中理论计算、有限元仿真和实验测试获得的微夹钳位移放大率分别为30.1,27.2和24.5。与有限元结果相比，理论计算结果偏高，偏差为9.6%。这是由于运动学计算时仅考虑了柔性铰链的弯曲变形，没有考虑其他变形造成的误差。而实验结果比有限元仿真结果低，这主要是由制造和装配误差造成的。

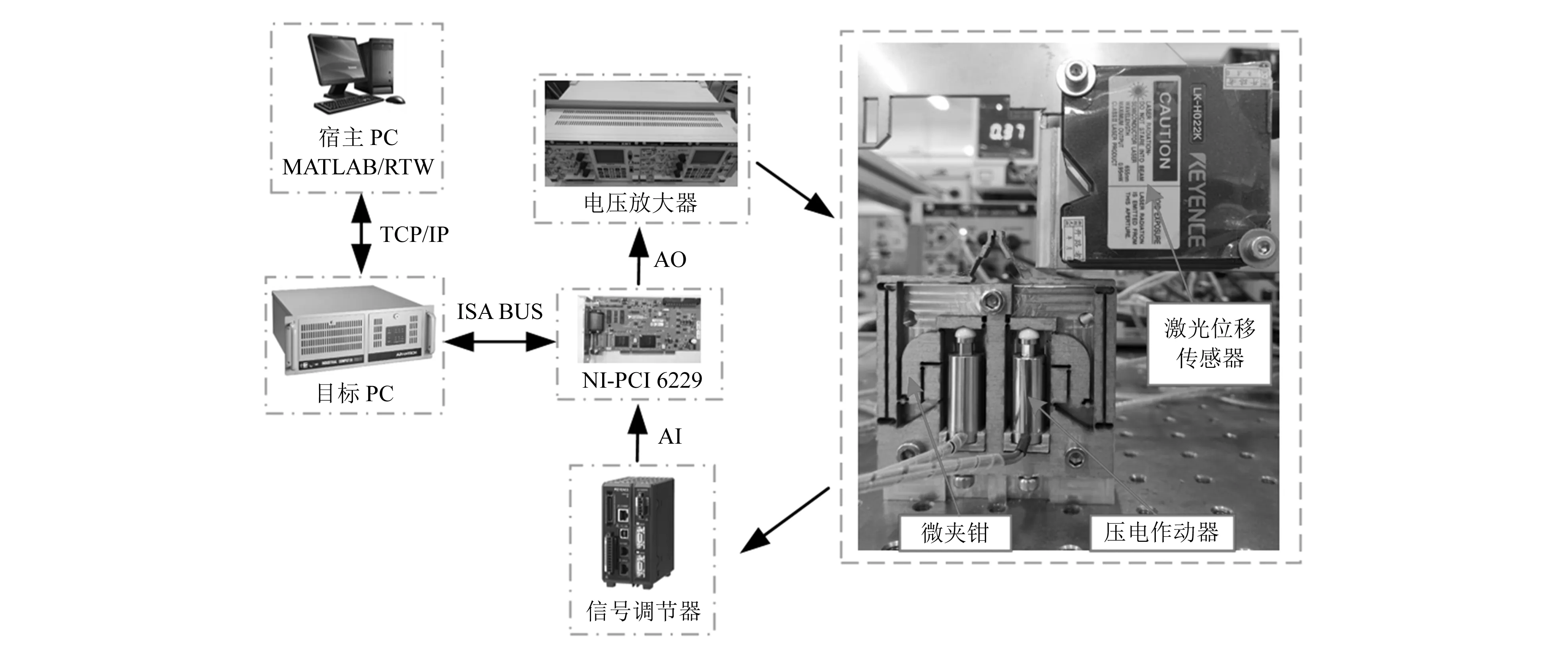
图8 实验装置

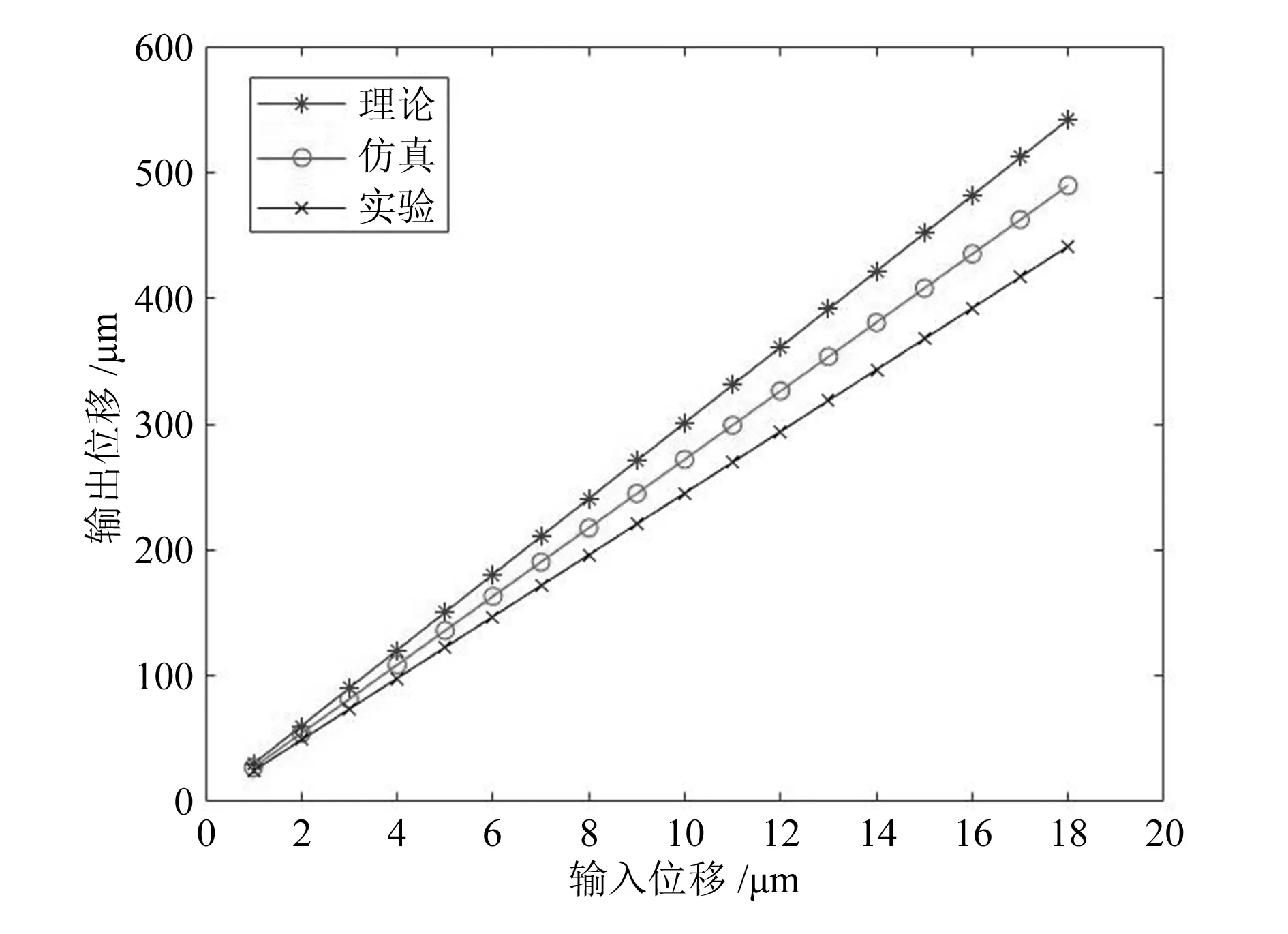
图9 微夹钳放大率

压电作动器输出位移与施加电压的关系如图10所示。当电压为120 V时，压电作动器输出的最大位移为18.1 μm。单个钳口的输出位移与施加电压的关系如图11所示。当电压为120 V时，单边的最大输出位移为441.8 μm，微夹钳的最大夹紧行程可达到882.3 μm。

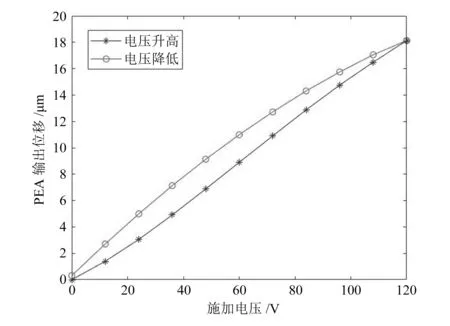
图10 压电作动器输出位移与施加电压关系

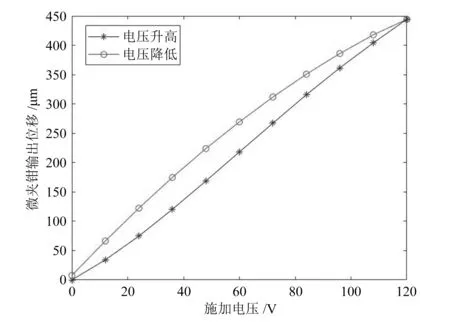
图11 微夹钳单边输出位移与施加电压的关系

下面通过对比本文及相关文献微夹钳的放大机构级数、放大率和夹持行程，来验证本文所设计的具有三级放大机构的微夹钳具有更大的放大率和夹持行程，见表3。

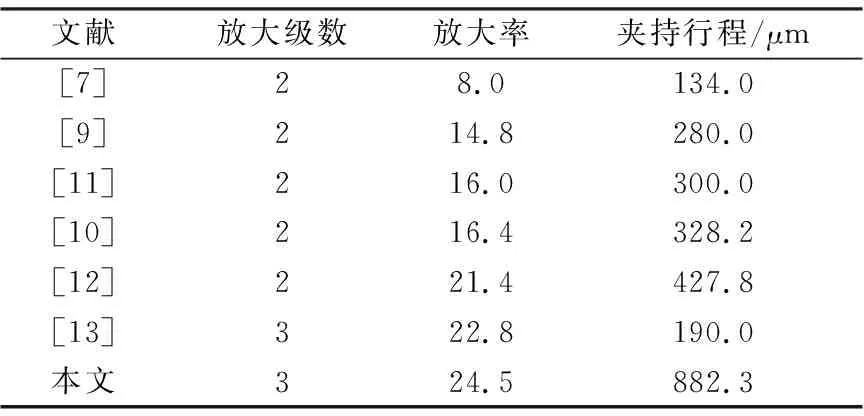
表3 微夹钳性能对比

5 结束语

微夹钳作为显微操作系统的关键部件，对显微操作系统的性能有显著影响。本文利用伪刚体模型，通过建立微夹钳的运动学、静力学和动力学模型，从理论上对微夹钳的结构进行了可行性分析，并利用有限元仿真分析软件确定了微夹钳的性能。本文提出的新型微夹钳，具备位移放大率高、夹持行程大和平动夹持的特点，可以满足大尺寸微小物体(427.8 μm及以上)稳定操作的需求。