具有网络外部性的软件市场的混沌动力学

刘 翠，周 伟

(兰州交通大学 数理学院，兰州 730070)

混沌系统是一种确定性的动态系统，它看起来是无序和随机的[1].混沌理论的起源可以追溯到Lorenz[2]对天气预报系统的研究.从数学上讲，混沌指的是一种非常特殊的不可预测性对初始条件非常敏感的确定性行为.混沌动力系统初始条件的微小变化可能会导致动力学行为的巨大变化.在过去的几十年中，人们研究了博弈模型的非线性动力学和混沌行为，在不同的情況下取得了显著的成果[3].尤其在金融领域，人们已经采用混沌理论使他们的预测更有经验上的鲁棒性[4].此外，一些研究人员对供应链的混沌行为、决策、排队系统等也进行了研究[5].

许多经济市场是动态的.从Katz等[6]开始，人们对网络外部性相关的问题进行了一系列的研究，网络外部性是指一个产品用户对另一个人的产品价值的影响[7].当产品对消费者的好处随着相同或兼容产品的用户数量的增加而增加时，就会产生这种效果[8].在软件市场上，由于文件兼容性、可移植性、经验共享和各种应用软件程序的可用性，可以广泛观察到网络外部性[7].

在实际环境中，软件公司发布不同质量产品的多个版本.“质量差异”一词是指任何软件在总功能上的差异.例如，Adobe公司发行了PDF文件阅读器软件的两个版本，即Adobe reader和Adobe acrobat[6].Adobe acrobat是一个高质量的版本，与低质量的对应产品Adobe reader相比，它具有更多的功能.Adobe reader已经发布，以吸引更多的消费者.提供低质量的版本有利于建立更大的网络，从而提高高质量版本的网络效用[7].与高质量的软件相比，低质量的版本更便宜，甚至是免费的.在一定条件下，低质量版本的发行可以促进高质量版本的销售[5].本文分析网络外部性存在下软件市场演化的动力学过程的目的，在于验证在具有网络外部性的软件市场中，低质量版本软件产品的发布可能导致的市场混沌现象.

1 模型构建

假设本文所建立的是一个完全垄断市场演化模型，在这个模型中，垄断厂商提供了同一类软件产品的两种不同质量版本的产品，即低质量版本的产品A和高质量版本的产品B.低质量版本通常是为了吸引消费者而生产的，它们的创建也是为了促进高质量版本的销售，这就是为什么他们以较低的价格提供或免费提供[5].

在本研究中，低质量版本A在时间段t的市场份额用x(t)表示，而高质量版本B的市场份额用y(t)表示，并且其中x(t)+y(t)≤2.消费者从低质量版本产品A和高质量版本产品B中获取的总效用分别为

U1(t)=M1(t)+I1,U2(t)=M2(t)+I2.

其中：Ii为消费者从软件产品i(i=1,2)中获得的内在效用，它是用户从产品自身固有的特性中获取的，为了简单起见，在此，本文假定消费者从产品中获得的内在效用和质量是相等的[7]；Mi(t)为消费者从软件产品i(i=1,2)中获得的网络效用，它是由软件产品的网络外部性产生的，并且会随着产品用户数量的增加而增加.因为低质量版本产品受到的网络外部性的影响不是很强烈，因此假设顾客从低质量版本产品A中获得的的网络效用与产品的质量成正比，从高质量版本产品B中获得的网络效用只与其网络规模有关，并且高质量版本产品的网络外部性强度高于低质量版本产品的[7].假设低质量版本产品A的网络外部性系数为θ1(I1/I2)，而高质量版本产品B的网络外部性系数为θ2，并且θ2>θ1>0.信息产品有一个突出的特点就是具有兼容性，因此信息产品的网络规模与产品兼容性系数有关，在此用α∈[0,1]来表示高质量版本产品和低质量版本产品之间的兼容性系数，α=0表明两个版本的产品是完全兼容的，α=1表明两个版本的产品是完全不兼容的[7].因此

M1(t)=θ1(I1/I2)(x(t)+αy(t)),M2(t)=θ2(αx(t)+y(t)).

考虑在具有网络外部性的信息产品市场中,消费者除了能从购买产品中获得基本效用之外，还能获得与产品网络规模相关的网络效用，消费者根据其购买产品所获净效用制定其购买决策[10].因此，根据上述分析将市场份额演化的过程定义为如系统(1)的动力学模型

(1)

其中:γ1>0和γ2>0分别表示低质量版本产品A和高质量版本产品B的市场演化速度;Q>0为所有消费者的总数量;ν1∈(0,1)和ν2∈(0,1)分别表示在每一个时间段内消费者放弃使用低质量版本产品A和高质量版本产品B的比例[7].

2 稳定性分析

为了求上述动力学模型的不动点，令

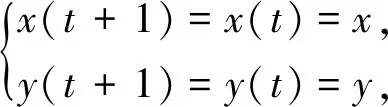
(2)

由此得到系统(1)的两个均衡点

均衡点E1和E2称为边界均衡点，是一个垄断均衡解[9].由稳定性理论，为了研究均衡点的稳定性，可以通过计算系统(模型)的Jacobi矩阵来分析[9].计算系统(1)在任意点的Jacobi矩阵为

(3)

其中：

J11=1-2γ1θ1(I1/I2)x-γ1(1+α)θ1(I1/I2)y+Qγ1θ1(I1/I2)-γ1I1-ν1;

J12=-2γ1αθ1(I1/I2)y-γ1(1+α)θ1(I1/I2)x+Qγ1αθ1(I1/I2)-γ1I1;

J21=-2γ2αθ2x-γ2(1+α)θ2y+Qγ2αθ2-γ2I2;

J22=1-2γ2θ2y-γ2(1+α)θ2x+Qγ2θ2-γ2I2-ν2.

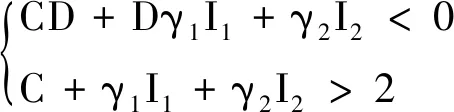
证明：将均衡点

代入式(3)，得到

J1=J(E1)=

(4)

其中:A=γ1[αI1θ2-I2θ1(I1/I2)];B=αν1θ2;C=Qγ1θ1(I1/I2);D=Qγ2θ2.

对应的特征方程为

P(λ)=λ2-Tr(J1)λ+Det(J1)=0,

(5)

这里Tr(J1)表示均衡点E1处的迹；Det(J1)表示均衡点E1处的行列式。其中：

(6)

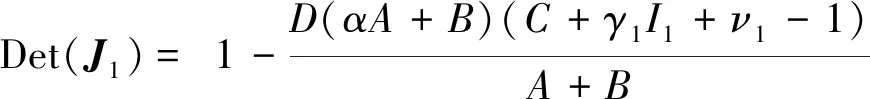
(7)

因此

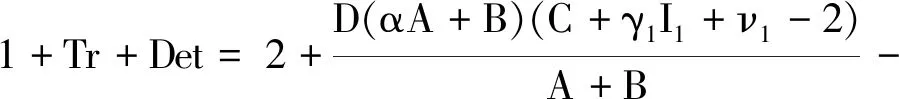
(8)

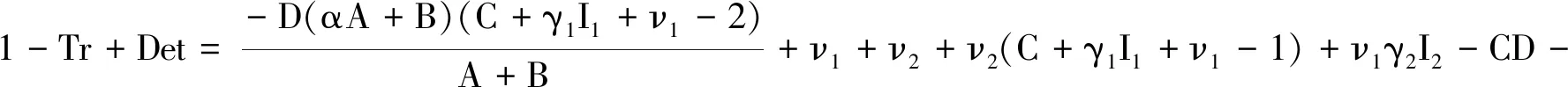
(9)

(10)

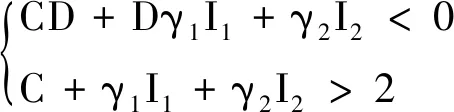
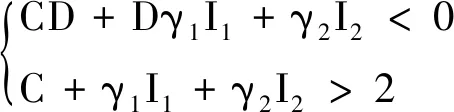
证明：将均衡点

代入式(3)，得到

J2=J(E2)=

(11)

其中:M=γ2[I1θ2-I2αθ1(I1/I2)];N=αν2θ1(I1/I2).

对应的特征方程为

P(λ)=λ2-Tr(J2)λ+Det(J2)=0,

(12)

这里Tr(J2)表示均衡点E2处的迹;Det(J2)表示均衡点E2处的行列式.其中:

(13)

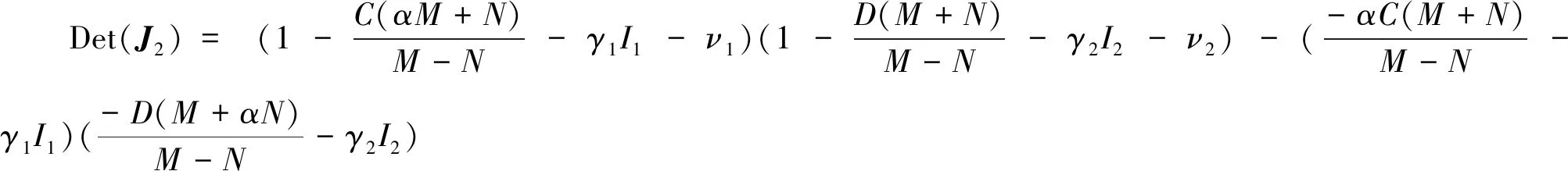
(14)

3 数值模拟

上一节对系统的均衡点进行了分析，在这一部分，本文主要讨论系统在不同参数范围下的复杂动力学现象，利用双参数分岔图、单参数分岔图及对应的最大Lyapunov指数图、吸引盆等工具来研究其动力学特性[9].在市场竞争和垄断环境下，由于网络外部性的影响导致低质量版本信息的产品市场混乱，因此本文主要将低质量版本信息产品A的各项参数作为主要研究对象，研究其动力学行为.

3.1 参数γ1和I1对系统稳定性的影响

本文希望低质量版本信息产品A的调整速度γ1具有一个稳定变化的趋势，对始于稳定参数空间区域的值，随着调整速度的增加，会失去其稳定性[9]，而且对于所构建的垄断系统模型，低质量版本信息产品A的内在效用的相关值会产生一定的分岔，基于以上分析，为讨论低质量版本产品A调整速度γ1和内在效用I1的变动对系统稳定性的影响，设定参数：I2=0.200 2，ν1=0.622 4，v2=0.622 4，Q=2，α=0.333 3，γ2=0.672 7，θ1=0.393 5，θ2=1.627 5，研究参数γ1和I1对系统稳定性的影响，如图1所示.

图1呈现了系统在参数空间(γ1,I1)的双参图，其中：1为深灰色；2为灰白色；4为浅灰色.深灰色区域表示稳定域，当(γ1,I1)的取值在这个区域时，系统将趋于一个稳定点；灰白色区域表示二周期区域，浅灰色区域表示四周期区域等等.

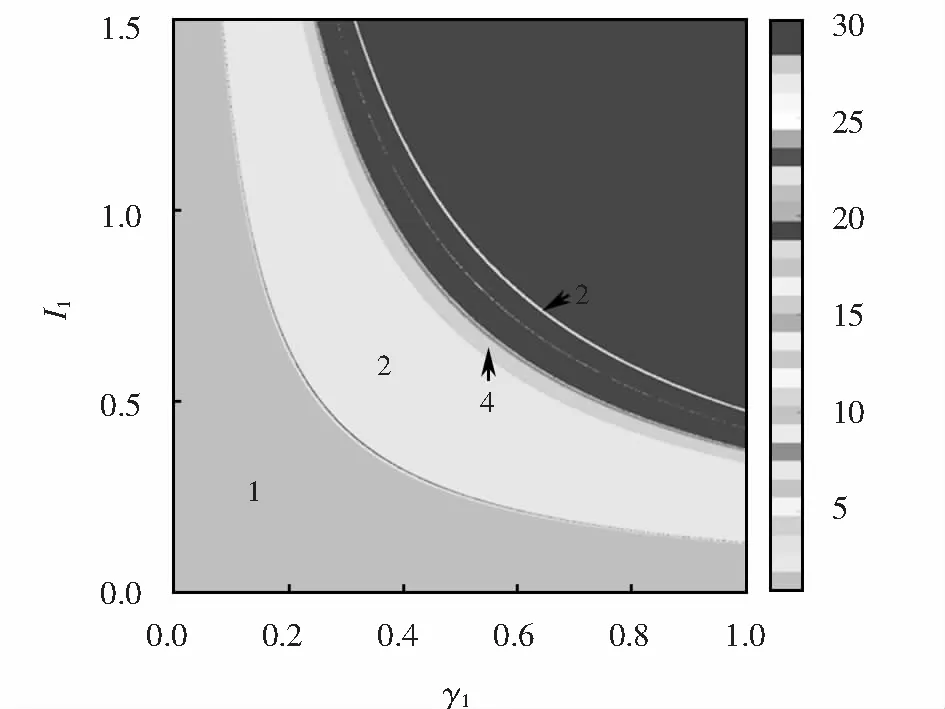
图1 系统在参数空间(γ1,I1)的二维分岔图Fig.1 Bifurcation diagram of the system in the parameter space (γ1,I1)

图2是在图1参数下关于γ1的单参图以及最大Lyapunov指数图.

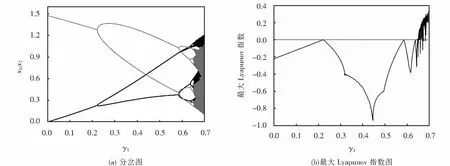
图2 系统(1)关于γ1的分岔图和最大Lyapunov指数图Fig.2 Bifurcation diagram and the largest Lyapunov exponent of the γ1 in system (1)

由图2可以看出，当最大Lyapunov指数小于0时，系统是稳定的；当γ1≥0.647 9时，最大Lyapunov指数开始出现大于0的情况，并且包含有部分小于0的瞬时情况，其中当最大Lyapunov指数大于0的时候，系统处于一个混沌状态，而小于0的时候，意味着系统出现了周期窗口.

图3是在图1参数下关于I1的单参图以及最大Lyapunov指数图.由图3可以看出，当I1≥0.552 3时，最大Lyapunov指数开始出现大于0的情况，并且也包含有极少部分小于0的情况，其中最大Lyapunov指数大于0的情况对应于系统的混沌状态，而小于0的情况代表着系统出现了周期窗口.

基于以上数值模拟分析，可以看出在垄断模式下，当低质量版本信息产品的调整速度或低质量版本信息产品质量都较小时，市场会稳定一些，而当其调整速度或内在效用逐渐增大时，会导致两个版本信息产品的市场份额发生周期变化，甚至出现混沌状态[7].

3.2 参数ν1和α对系统稳定性的影响

这一小节，本文讨论每一时间段内消费者放弃使用低质量版本产品A的比例和两个版本之间的兼容性的变动对系统稳定性的影响，假定其他参数固定：I1=0.244 3，I2=0.579 6，ν2=0.000 016 20，Q=2，γ1=0.612 9，γ2=0.612 9，θ1=0.314 0，θ2=1.776 7，研究参数ν1和α对系统稳定性的影响.

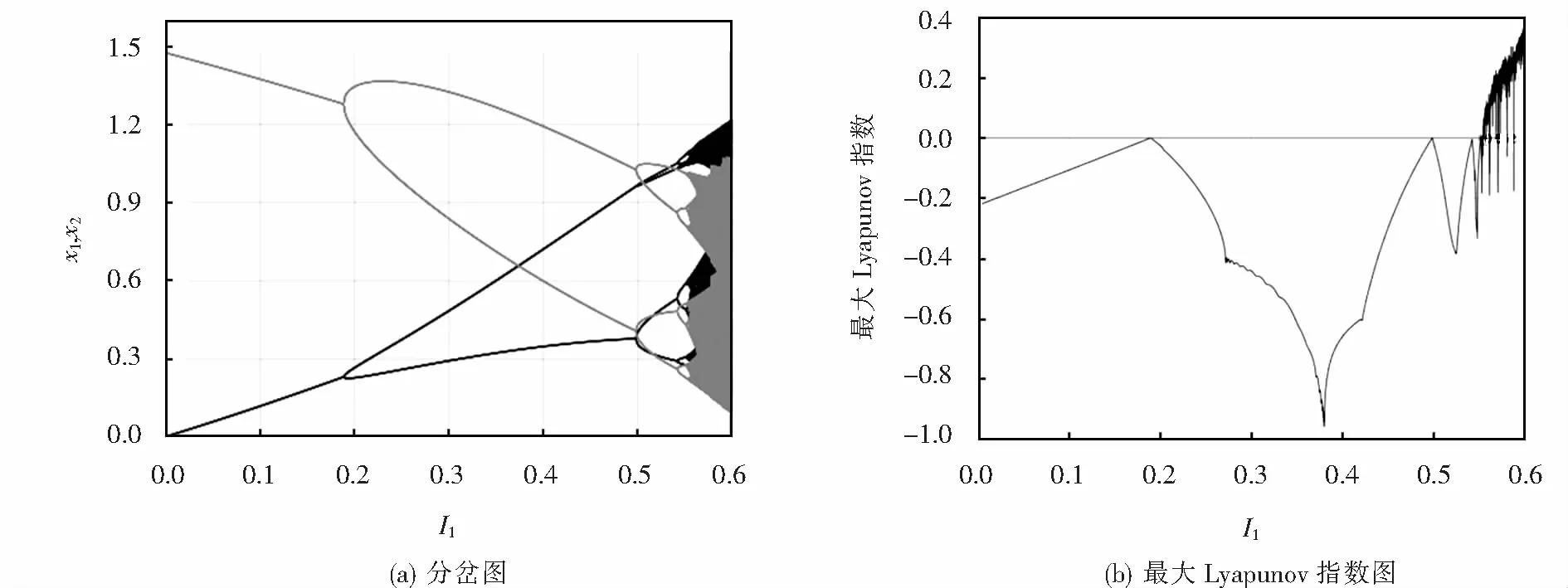
图3 系统(1)关于I1的分岔图和最大Lyapunov指数图Fig.3 Bifurcation diagram and the largest Lyapunov exponent of the I1 in system (1)

图4展示了系统在参数空间(ν1,α)的双参图，其中：2为灰白色；4为浅灰色；8为深灰色.灰白色区域表示二周期区域，浅灰色区域表示四周期区域，深灰色区域表示八周期，黑色表示逃逸区域.

图5是在图4参数下关于ν1的单参图以及最大Lyapunov指数图.当最大Lyapunov指数小于0时，系统是稳定的；当ν1≥0.268 9时，最大Lyapunov指数开始出现大于0的情况，并且包含有小于0的瞬时情况，此时最大Lyapunov指数大于0意味着系统处于混沌状态，小于0意味着系统出现了周期窗口.

图6是在图4参数下关于α的单参图以及最大Lyapunov指数图.

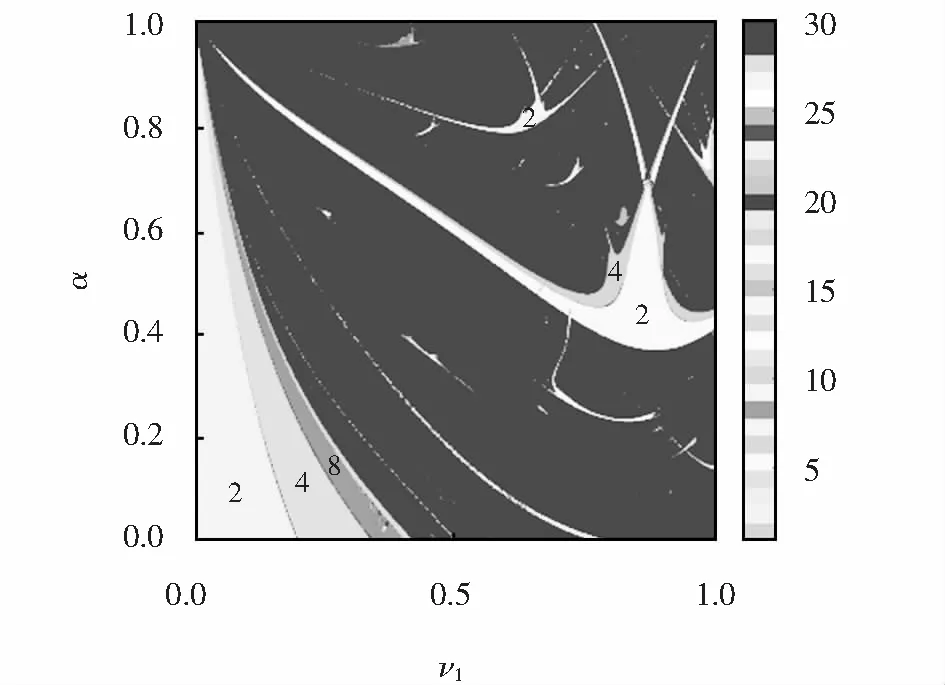
图4 系统在参数空间(ν1,α)的二维分岔图Fig.4 Bifurcation diagram of the system in the parameter space (ν1,α)

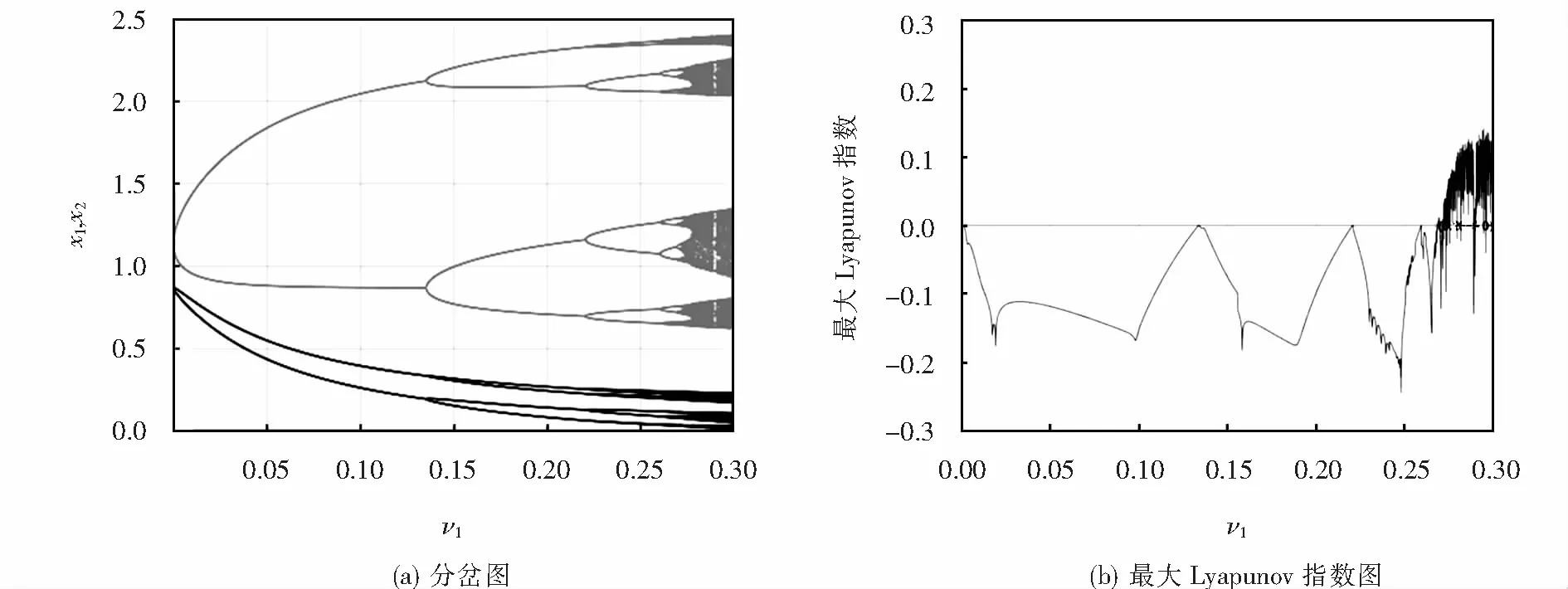
图5 系统(1)关于ν1的分岔图和最大Lyapunov指数图Fig.5 Bifurcation diagram and the largest Lyapunov exponent of the ν1 in system (1)

由图6可以看出，当α≥0.337 1时，最大Lyapunov指数开始出现大于0的情况，同样也包含有极少部分小于0的情况，其中最大Lyapunov指数大于0的时候意味着系统处于混沌状态，而当最大Lyapunov指数小于0的时候意味着系统出现了周期窗口.在其他参数固定不变时，随着低质量版本信息产品A的每一时间段内消费者放弃使用低质量版本产品A比例ν1和两个版本之间的兼容性系数α足够大时，系统将出现奇异吸引子[7].

图7是在固定参数：I1=0.244 3，I2=0.579 6，ν2=0.000 016 20，Q=2，γ1=0.612 9，γ2=0.612 9，θ1=0.314 0，θ2=1.776 7，随着参数ν1和α的增大奇异吸引子的演化及吸引盆的变化，其中吸引盆的灰白色部分表示吸引子的吸引域，深灰色部分表示吸引子的逃逸区域.

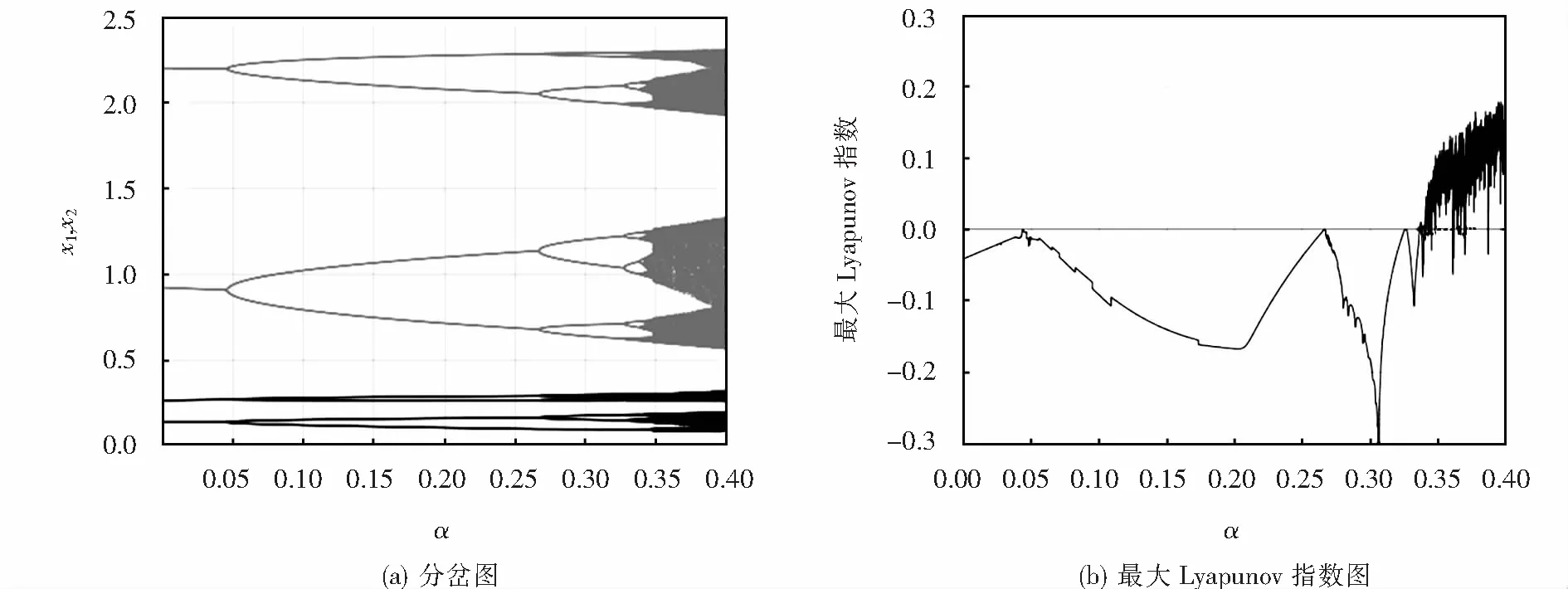
图6 系统(1)关于α的分岔图和最大Lyapunov指数图Fig.6 Bifurcation diagram and the largest Lyapunov exponent of the α in system (1)

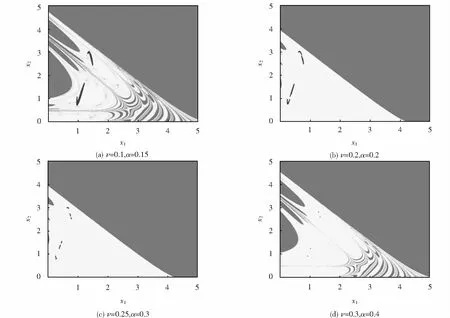
图7 吸引子的演化及其吸引盆Fig.7 Evolution of attractor and its basin of attraction

以上数值模拟结果表明，在垄断模式下，当低质量版本信息产品被放弃的比例越多或低质量版本信息产品A和高质量版本产品B两者兼容性都逐渐增大时，高质量版本信息产品B的市场份额会逐渐减少，接下来可能造成两个版本信息产品的市场份额发生倍周期分岔现象，甚至出现混沌状态[7].当完全垄断市场提供的信息产品之间的兼容性较小时，厂商更愿意提供低质量版本的产品[7].

4 结语

本文在离散时间下，建立了一个具有网络外部性的完全垄断市场演化模型，分析了模型均衡点的稳定性，着重讨论了低质量版本信息产品在网络外部性条件下各项参数对产品市场份额的影响，并且对不同参数下的双参图、分岔图、最大Lyapunov指数、奇异吸引子以及吸引盆进行了分析.研究表明，在竞争市场中低质量版本的信息产品的发布可能会促进高质量版本信息产品的销量，但也有可能造成市场出现混沌现象，因此厂商在提供低质量版本信息产品时，一定要谨慎设计其质量，既要满足消费者的基本需求，也要避免引起市场出现混沌现象[7].