无人机海上溢油跟踪监测系统设计及仿真

覃睿，闫玲，陈子健

（中国民航大学 交通科学与工程学院，天津 300300）

环境监测是可持续发展的关键，目标环境属性在时间和空间上是可变的。环境监测一般包括现场调查、样品采集、分析测试、数据处理和综合评价等（吴季友等，2020）。随着目标环境监测范围不断扩大，劳动强度明显增加。时间和空间的变化也要求监测的方法必须足够有效，以便能够即时了解环境状况。无人机作为现代科技产物，可通过搭载各类传感器和测量设备，在恶劣的自然条件下精确监测环境变化，如监测森林火灾、地震、放射性废物以及海洋内部和表面各种类型的污染等（Cook，2007；Casbeer et al，2006；Dunbabin，2012）。在面对如实时监测海上溢油等监测区域较大的情况时，近年来普遍采用高空卫星监测与低空航空监测相结合的手段（李欢等，2017）。利用星载合成孔径雷达（SAR）遥感对海洋进行大范围溢油监测，之后利用低空航空监测检验遥感监测结果并对溢油区域进行进一步详细监测，提供实时信息（孙健等，2014；史一凡等，2014）。

无人机在现代监测中凭借部署快、成本低的特点已成为未来低空航空溢油监测的方向。张婷等（2018）研究了紫外与SAR 技术集成于无人机联合用于溢油探测的方法；曲小同等（2019）建立了海上无人机溢油监测巡航优化模型，利用改进蚁群算法求解；任广波等（2019）以无人机高光谱遥感为手段，研究了海面溢油检测方法。但上述无人机溢油监测手段都仅使用了单架无人机，对于小范围环境监测问题，使用单个无人机应该足够，然而，当监测溢油漂移和扩散时，无人机搜索和监控的环境区域不断扩展，单个无人机可能产生以下限制：缺乏全局信息，导致监测过程易受传感器信息误报、环境信息变化等因素的影响，导致决策不周、探测效率低下；由于环境信息有限，单个无人机可能会陷入局部极值，导致误判；一旦单个无人机失效，任务将无法完成（Huang et al，2020）。使用一定数量的简单、便宜的无人机系统比使用单一的复杂、昂贵的无人机成本更低，且使用多个无人机不仅可以通过降低故障概率增加系统的鲁棒性，还可以在时空变化的情况下，对环境进行多重采样提高测量的准确性。

由于使用多个无人机进行溢油监测会增加系统的复杂性，因此如今大多数多智能体的研究主要集中在智能体集群编队和协调个体之间的距离等方面，其主要目标是实现编队控制目标、避免碰撞和向预期目标收敛（Liu et al，2021）。通常希望智能体之间形成固定或期望的距离，以避过障碍物。当智能体的运动需要跟随监测溢油而具有灵活性时，现有的方法会存在一定限制。溢油在海上的漂移扩散是一个监测范围不断扩展的时空变化问题，需要无人机群具有灵活性，故本文提出多无人机系统的柔化编队协议，该协议在多智能体执行任务时具有灵活性。在此系统下，整个系统的状态都取决于环境和主体间的相互作用。同时，该协议也可广泛应用于无人机群对不同尺度的时空环境现象进行跟踪和监测。

1 无人机监测海上溢油场景总体架构

1.1 总体方法概述

本文的主要假设包括无人机可以使用GPS 或GLONASS 等定位设备实现自主定位，使用GPRS数据网络等进行通信，同时能够携带设备，进行溢油污染采样，测量海上溢油污染的浓度。因此，本文假设利用高空卫星获取SAR 图像确定溢油大致位置后（李颖等，2017），无人机能够到达预定位置，测量溢油污染的浓度，并在网络中彼此分享污染物浓度信息和位置信息。一旦计算出新的位置，无人机可在单位时间内到达该位置。集群中的每架无人机都可看作一个具有智能行为的智能体，每个智能体一般只需处理与自身相关的局部信息，进行自主活动，但同时又具有合作的能力。针对任务目标，集群中的各无人机可动态地规划各自的运动序列，采用分布式控制，而不是集中规划。

考虑无人机集群中包含n 个无人机智能体ai，i沂（1，2，…，n），在海上的位置确定为Pi=（xi，yi），集群的中心位置为P0=（x0，y0），是各智能体位置的平均值，中心点O 即为后续坐标系统的原点。

无人机在系统中的控制输入为F：

其中，Fz为无人机控制器输出的分量，由跟踪控制器生成；F渍为无人机控制输出的另一分量，由人工势场法得到。

1.2 无人机群监测系统架构

图1 显示了无人机之间，无人机群与海上溢油环境之间以及无人机群与地面控制中心间的相互作用。集群中的无人机根据位置传感器和污染传感器测量的海上溢油浓度变化和网络中其他无人机的位置进行不断的迭代调整，并通过基站将溢油信息传送至地面控制中心，以便决策者做出下一步行动计划。过程中需要计算单个无人机的下一个目的地，然后移动至此。无人机集群的形成取决于溢油随时间变化的污染形态分布。因此，基于无人机污染传感器测量的数值，采用模糊PID 控制器进行处理，产生分量Fz。另一方面，利用人工势场法保持多智能体分布的一致性，避免碰撞。

图1 无人机群溢油监测系统架构

基于多智能体系统的无人机集群逻辑结构模型（梁晓龙等，2018）如图2 所示，图中的传感器包括污染传感器和定位传感器，如图3 所示。污染传感器负责测量污染浓度并记录在信息处理器中，将记录的污染信息输入无人机跟踪控制器，生成无人机控制输出的分量Fz。同时，定位传感器获得位置信息，通过网络与其他无人机共享，并从网络中接收其他无人机的位置信息，利用人工势场法生成无人机控制输出的分量F渍，以保证无人机之间的安全间隔。最后，结合控制模块的结果，驱动无人机的发动机或推进器将其移动到所期望的目的地。这个算法不断循环，使得整个集群对污染的变化不断做出反应。事实上，整个系统的形成取决于环境和主体间的相互作用。同时，该算法也适用于使用无人机群对不同时空尺度的其他环境现象，如藻类和放射性废弃物等进行跟踪和监测。

图2 无人机集群逻辑结构图

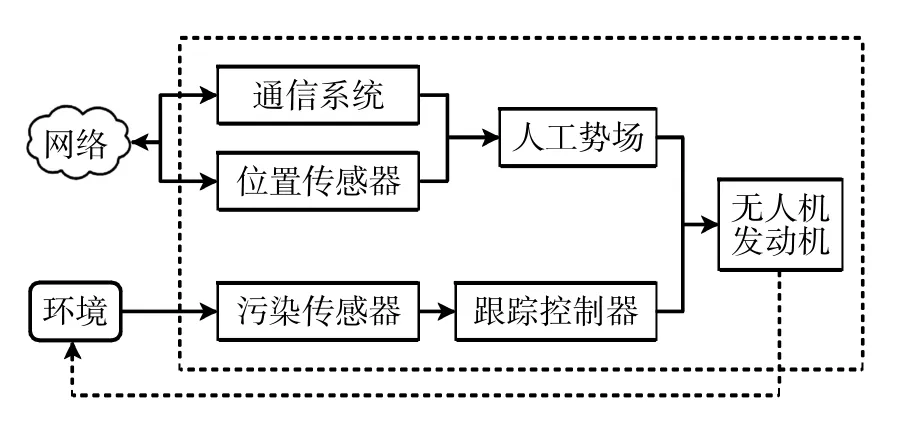
图3 单个无人机工作流程结构图

2 海上溢油模型

现有的溢油模型理论将海上溢油过程大体分为四个阶段：溢油扩散、溢油漂移、溢油蒸发和溢油乳化（邹长军等，2017）。本文中无人机跟踪监测的重点为前两阶段。为验证本文对无人机控制器设计算法的可靠性和真实性，利用溢油的数值模型对提出方法的性能进行模拟和评价。在数值仿真中，溢油的漂移和扩散过程必须符合溢油运动的基础理论。

2.1 溢油扩散模型

由于溢油在海上的扩散过程具有随机性，可用蒙特卡罗方法进行描述。蒙特卡罗方法（Monte Carlo Method），又名统计模拟方法，是20 世纪40年代中期因科学技术和电子计算机的发展，而被提出的一种以概率统计理论为指导的数值计算方法（裴鹿成等，1980）。求解溢油扩散问题时，利用扩散现象的随机性，通过给定时间尺度、湍流强度和随机粒子数，以求得粒子的扩散。扩散所用的随机数由正规随机数方法产生（娄安刚等，2000）。

n 个粒子在t=0 时，设x=y=z =0；在t=t0时，进入网格内粒子的个数可换算为溢油浓度L。这样计算出的溢油浓度在粒子数较少时可能会出现错误，需作适当的平滑。例如，将周围的9 个格子中的粒子数进行平均，再计算溢油浓度，即可抑制分布不规则的极端值。

溢油面积可根据Fay（1971）的海上溢油模型进行计算，溢油面积A 为：

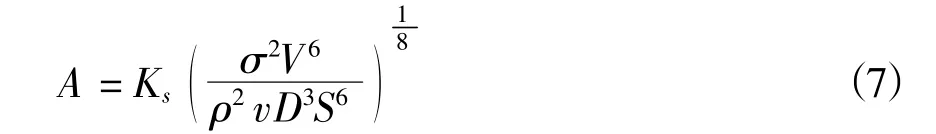
其中，Ks为待定系数，滓为净表面张力，V 为溢油体积，D 为石油表面活化剂的扩展系数，籽为溢油密度，S 为油的溶解度。

由于上式中的Ks、S 和D 难以确定，所以一般的计算中使用经验公式计算海上溢油的最终溢油面积：

2.2 溢油漂移模型

海上发生溢油事故时，油膜除了发生扩散运动外，还会在海面风应力的推动作用和海流的携带作用下发生漂移运动。油膜的漂移涉及的因素很多，较为复杂，截至目前尚无较为理想的数学模型。鉴于此，以下采用Webb 等（1970）建立的基于专家经验的经典海军模型漂移方程，在该模型下，设油膜的漂移速度为，则：

其中，Vt为海流速度矢量；Vw为海上风速矢量；Kw为海流漂流系数，常选取0.035。

经过驻t 时间后，油膜的中心位置O 为：

将（6），（7）合并，得：

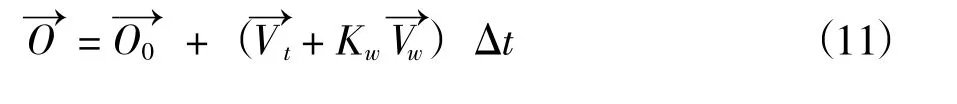
3 无人机控制跟踪系统

3.1 无人机控制跟踪器

PID（Proportion Integral Differential）控制是控制系统中较为成熟且应用最为广泛的控制器（Chen，2012），无人机溢油跟踪监测系统应用PID控制器的目的是希望根据溢油漂移及扩散状况，利用控制器输出的力Fz作用于无人机，使无人机从当前位置运动到溢油边界的目标位置。其表达式为：

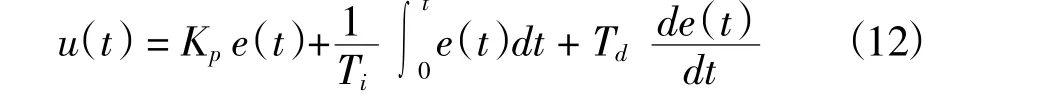
将上式离散化，得：

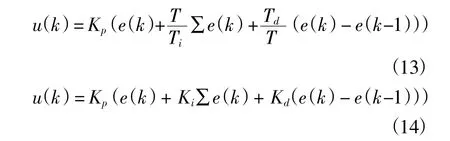
其中，e（k）为现在位置与目标位置之间的偏差；Kp，Ki，Kd分别表示比例、积分和微分增益。

考虑到无人机不能直接检测到溢油边界点，所以采取一种有效的措施，设置二进制污染浓度传感器，允许无人机越过溢油边界曲线：

其中，Si为在i 点二进制污染传感器读取数值，L0为污染传感器可识别浓度的最小值，Li为i 点的实际污染浓度。在Si（t）=1，Si（t+1）=0 或者Si（t）=0，Si（t+1）=1 时，可以看作无人机穿过溢油边界。上述两种情况都含有污染浓度的阶跃变化，由于无人机在寻找到目标点之前处于匀速运动状态，因此i（t）和i（t+1）两个相邻采样点之间的中点R 为污染边界点，即无人机目标位置：

为避免通过大量的实验调节PID 参数，缩短调节时间，引入模糊PID 控制。模糊PID 控制是在上述PID 算法的基础上，为提高控制器效率和鲁棒性而采用的方法（Gomez et al，2011）。在模糊PID 控制器中输入位置误差和误差变化率，运用模糊控制理论，将专家调节的知识库转化为模糊推理机制，利用模糊规则实现对PID 参数的整定。根据输入量e（k）和ec的不同组合，对应不同Kp、Ki、Kd的控制规则，使输入变量在不同阶段达到较好的控制效果（毛赫等，2018）。Kp、Ki、Kd有49种模糊规则，可通过Matlab 中的模糊规则编辑器编辑，并对其进行模糊推理和解模糊，得出模糊修正值Kp、Ki和Kd，完成对PID 参数的整定。Kp、Ki、Kd整定后的值为：

其中，Kp的作用是在偏差产生时，控制器可立刻进行控制，减少稳态误差。Ki用于消除震荡，提高控制精度。Kd可以改善动态特性，缩短调节时间。

3.2 人工势场法

本文希望将无人机集群的个体按均匀分布的方式排列，以获取更大的分布面积，因此采用人工势场法（曲成刚 等，2014）。以三个无人机i，j，k为例，假设各无人机具有相似极性的相同电荷，它们会互相排斥，但仅局限于在集群中心的垂直方向，每个智能体与集群中心的距离由跟踪控制器控制。每个智能体在人工势场中形成的力可确定方程中的F渍。根据库仑定律，其中qi和qj代表粒子i 和j 的电荷，且k抑9 伊109，它们之间的排斥力为：

智能体i 受到j 的力的垂直分量为：

根据正弦性质可得：

结合上式得：

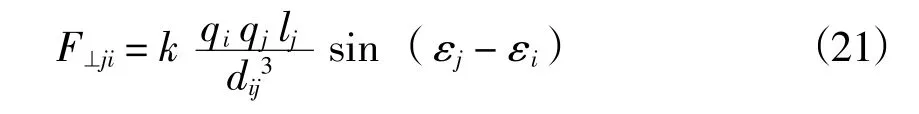
k 对i 的斥力与j 相同，因此，i 受到合力的垂直分量为：

其中，K 为正增益系数，j沂[1，n]，且j屹i ，n =N+，dij、lj、着i、着j 的示意图如图4 所示。

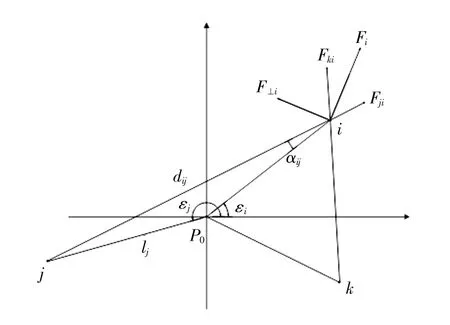
图4 无人机人工势场法受力示意图

使用人工势场法可使每个智能体都能自动找到合适的位置和平衡点，使系统在执行任务期间保持鲁棒性。

4 模拟仿真

模拟仿真的目的是基于以上所提出的方法，利用Matlab 软件评估无人机拟合变形油膜轮廓的性能。本文选取菲律宾东海岸及太平洋静风条件下的数据进行仿真，洋流数据来自国家海洋科学数据中心在线数据库（http://mds.nmdis.org.cn/），表1 为2017 年4 月15—24 日共10 天西北太平洋海域（125毅E—140毅E、15毅S—25毅N） 的海流速度与海流方向数据。

表1 西北太平洋海域海流速度与方向（2017.4.15—2017.4.24）

4.1 溢油漂移扩散仿真

首先模拟海上溢油，在模拟每次迭代的浮油之后，虚拟无人机将搜索和跟踪计算机生成的溢油。本文算法面向的主要环境是沿海地区和海洋，水平尺度远远大于垂直尺度，故运用Matlab 生成二维模型进行简化处理。其中，前文公式中扩散系数Kx=2 伊105cm2/s，Ky=2 伊105cm2/s，网格间隔设为驻x=50 m，驻y=50 m，时间驻t=60 s（娄安刚等，2000）。根据公式，假设溢油量为10 t，在静风条件下，海上风速为0耀0.2 m/s，本文取海上风速为0，根据上表数据得出平均海流速度约为0.15 m/s，平均流向为88.62毅，在5耀20 h 内溢油仿真的结果如下图5—图8 所示，图中的油粒子代表了溢油扩散范围，图侧的色标表示溢油的浓度（单位为mg/L）。由图可知，油膜随时间的变化而不断漂移和扩散，浓度也随时间在不断变化。

图5 溢油漂移扩散5 h 后的位置

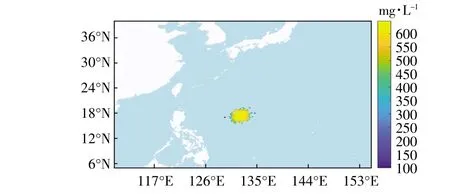
图6 溢油漂移扩散10 h 后的位置

图7 溢油漂移扩散15 h 后的位置

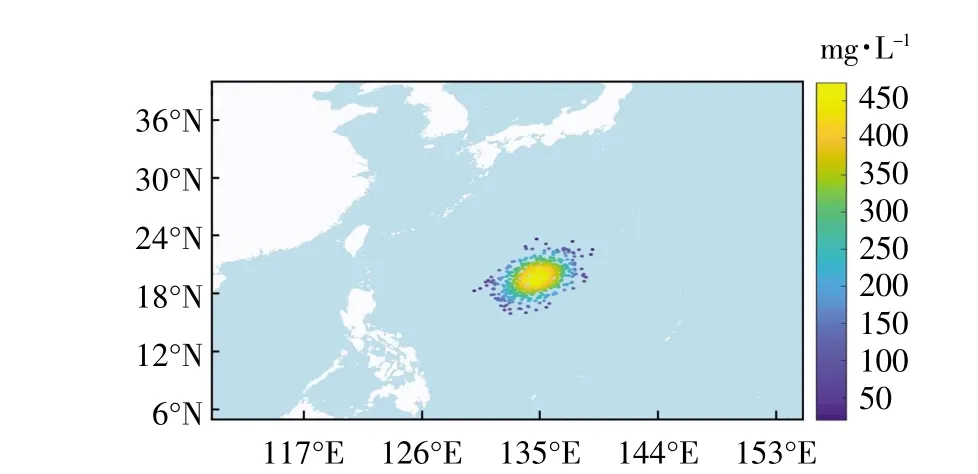
图8 溢油漂移扩散20 h 后的位置

4.2 无人机跟踪仿真

在模拟每次迭代的浮油之后，虚拟无人机将搜索和跟踪计算机生成的溢油。设计出的无人机群跟踪系统将模糊PID 控制器与人工势场法相结合，控制无人机到达溢油边界且互相存在安全间隔。本文仿真了10 架无人机跟踪监测溢油的场景，如图9—图12 所示，连接无人机的虚线代表无人机编队的轮廓线，其目的是拟合海上溢油边界，这是通过在无人机集群中心周围位置进行三次样条插值实现的。

图9 无人机追踪溢油漂移扩散5 h 的场景

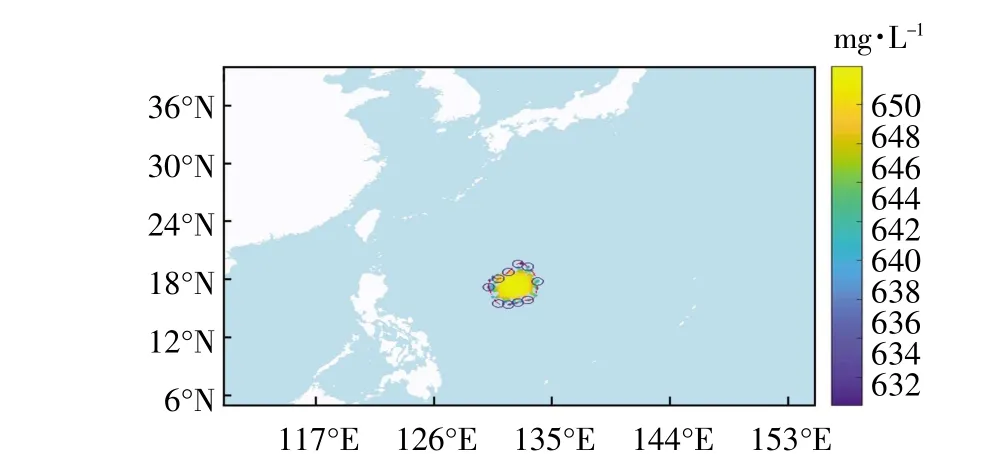
图10 无人机追踪溢油漂移扩散10 h 的场景

图11 无人机追踪溢油漂移扩散15 h 的场景

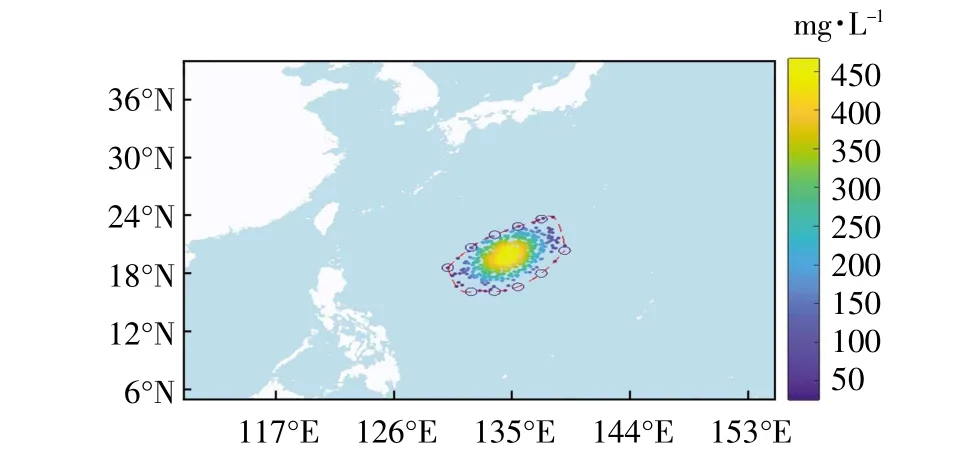
图12 无人机追踪溢油漂移扩散20 h 的场景

4.3 仿真结果与讨论

无人机覆盖的溢油区域的面积与实际溢油面积的重合率为：

其中，A 为溢油面积，B 为无人机覆盖区域面积。

根据前文模拟仿真结果计算出无人机所覆盖的面积与海上溢油面积及其在5耀20 min 时的重合率，绘制出折线图，如图13 和图14 所示。由图14 可知，本文设计的无人机跟踪控制系统使无人机覆盖面积与海上溢油的面积随时间变化的重合率控制在70%以上，最高可达80%左右，且具有良好的稳定性。溢油进入海洋后，油膜面积不断变大，油膜厚度变小，边缘溢油浓度也逐渐变小。无人机通过测量溢油浓度确定溢油边缘，故当溢油浓度降低，无人机群对溢油的覆盖面积也有所降低，产生测量误差。

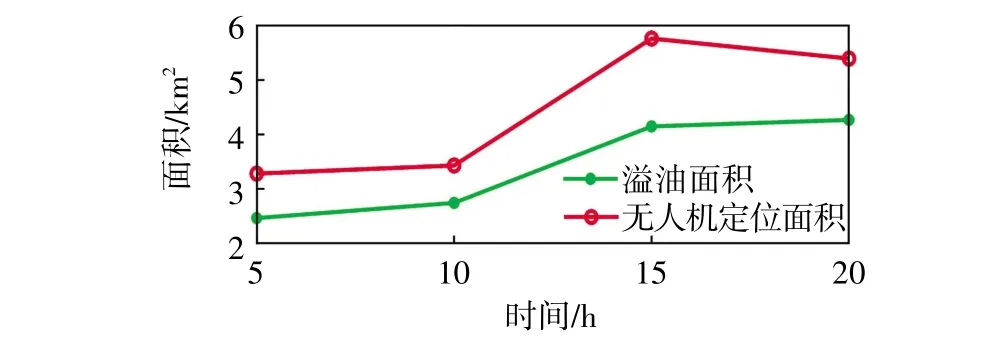
图13 溢油面积与无人机覆盖面积

图14 溢油面积与无人机覆盖面积重合率

缘 结论

本文提出了一种针对溢油污染的自适应无人机群跟踪方法。该方法依赖于周围环境变化，更适合于监测和跟踪随时间变化的环境现象。本文首先建立了一个无人机跟踪框架，将模糊PID 控制器与人工势场法相结合，提高鲁棒性。模糊PID 控制器使无人机群覆盖了大部分溢油范围，而人工势场法保持了无人机集群的编队。最后通过仿真验证了该方法的有效性。

仿真结果表明，该方法对海上溢油污染监测的覆盖率可以达到80%，能够在溢油污染漂移和扩散的不同阶段保持良好的跟踪效果。本文在理论上具有可行性，但笔者仅仿真了无人机监测静风条件下海上溢油的漂移和扩散，其他气候条件下的覆盖率还有待进一步研究；且仿真时采用了溢油模型模拟溢油的漂移和扩散而非真实的溢油状况，与实际情况存在误差，在实际应用方面还有待完善。未来，该方法应在大规模、复杂的海面环境上进行现场试验和模拟，测试其适用性和鲁棒性。